Четырехволновое взаимодействие в многомодовом волноводе с тепловой нелинейностью в схеме с попутными волнами накачки

В последние годы пристальное внимание уделяется исследованию четырехволновых взаимодействий в волноводах [1-6]. Это обусловлено возможностью высокой концентрации энергии взаимодействующих волн в волноводах на больших длинах взаимодействия, что позволяет значительно повысить эффективность четырехволновых преобразователей при использовании сравнительно маломощных источников излучения.

Для решения задач нелинейной адаптивной оптики, обработки в реальном времени оптических сигналов, изображений с использованием четырехволновых преобразователей излучения используются многомодовые волноводы в схемах со встречными и попутными волнами накачки. Если в схеме со встречными волнами накачки при четырехволновом взаимодействии волна с обращенным волновым фронтом распространяется навстречу падающей волны, то в схеме с попутными волнами накачки волна происходит обращение лишь поперечной составляющей волнового вектора падающей волны. Выбор схемы взаимодействия определяется решаемой с использованием четырехволновых преобразователей излучения задачей [7; 8].

Любая оптическая система, в том числе и четырехволновой преобразователь излучения, осуществляет преобразование комплексной амплитуды падающей на него волны с определенной точностью, которая существенным образом за- висит от вида нелинейной среды, в которой реализуется четырехволновое взаимодействие [9–11]. С использованием метода функции размытия точки (ФРТ) проведено исследование пространственных и временных характеристик четырехволновых преобразователей излучения в зеркальном, параболическом волноводах в схеме со встречными волнами накачки в средах с керровской, резонансной, тепловой нелинейностями [6; 12; 13], в схеме с попутными волнами накачки в параболическом волноводе с керровской нелинейностью [14].

Несомненный интерес представляет исследование качества обращения волнового фронта четырехволновым преобразователем в схеме с попутными волнами накачки в многомодовых волноводах с тепловой нелинейностью.

1. Функция размытия точки четырехволнового преобразователя в многомодовом волноводе с тепловой нелинейностью

Рассмотрим вырожденное четырехволновое взаимодействие с попутными волнами накачки в волноводе с тепловой нелинейностью, расположенном между плоскостями z = 0 и z = / . На волновод падают две волны накачки с комплексными амплитудами А_г и A 2 и сигнальная волна с комплексной амплитудой A 3 . В результате вырожденного четырехволнового взаимодействия ( to + to-to = to ) генерируется объектная волна A 4 (рис. 1). Исходное уравнение Гельмгольца, описывающее такое взаимодействие, есть

V ² + k ² n ² ( x ) + 2k- f— ) 5 T - 2 ik a n ₁ ( dT )

' ( л + A^ = 0.   (1)

N

5 T 32 ( x , z ) = ^ 5 T p 2 ( z ) f p ( x ). p = 0

Здесь A = E A j , n ( x ) - показатель преломления;

j = 1

k = —, a - амплитудный коэффициент поглоще- c

Здесь 5 T p 12 - спектры температурных решеток.

Подставив (4) в (2) с учетом (3), получим:

ния; — - циклическая частота; с - скорость света в вакууме; 5 T - изменение температуры, обуслов-

d ² 5 T^      ,. d ² f

-T- +⁵ T p 1 f f p -JJ p dx = dz              d x

ленное выделением тепла при поглощении излу-

-

чения; n ₁ – значение показателя преломления на оси волновода; n^- - термооптический коэффици- dT

NN

777 EE a 1 n a 3 5 ^r n , 5 , p ^exp^[ - i ^{( e} n -p* ) z ^]. ^Л c p ^Р n = 0 k = 0

ент; x – поперечная координата.

Уравнение (1) необходимо дополнить уравнением Пуассона

V ² 5 T + 2^— AA* = 0.                        (2)

^Л c p Р

Здесь Л - коэффициент температуропроводности; С р - удельная теплоемкость; р - объемная плотность вещества.

Изменение температуры представим в виде суммы медленно и быстро меняющихся в зависимости от поперечной координаты x составляющих 5 T ( x , z ) = 5 T ₀ ( x , z ) + 5 T ₃₁ ( x , z ) +

^{d 2 5} T p 2 dz ²

^{+ 5} T p 2 f ^f p

d ² x

dx =

NN

= -777 EE a 2 m ^a 3 5 ^Г m , 5 , p ^exP^{[ -} i ^{( e} m -^в 5 ) ^z 1 ^Л c p ^Р m = 0 k = 0

Здесь Г n , ₅ , _p = f f n ( x ) f₅ *( x ) f_p ( x ) dx - интеграл перекрытия, характеризующий эффективность взаимодействия трех мод волновода. При выводе уравнения (5)-(6) использовалось условие орто-нормированности мод волновода: f f n ( x ) f m ( x ) dx = 5 _nm , где 5 nm - символ Кронекера. Для решения уравнений (5), (6) необходимо задать как вид мод

+ 5 T ₉ ( x , z ) + 5 T oi ( x , z ) + 5 T oо ( x , z ). 32          31          32

Здесь 5 T o ( z ), 5 T 31 ( x , z ), 5 T 32 ( x , z ) - изменения температуры, обусловленные распространением волн накачки, интерференцией волн накачки с сигнальной волной. В общем случае в среде записываются две температурные решетки. Однако если одна из волн накачки, например вторая волна, не когерентна первой волне накачки и сигнальной волне, то в нелинейной среде записывается одна температурная решетка ( 5 T 31 ).

Разложим взаимодействующие волны по модам волновода, не содержащего тепловой нелинейности:

N

^A j ( ^x , ^z ) = E a jn ^{( z} ) f n ^{( x} , ^z )> j = ¹ 4.                   ⁽³⁾

n = 0

волновода, так и граничные условия на изменение температуры на передней и задней гранях волновода.

В приближении заданного поля по волнам накачки, без учета их самовоздействия и малом коэффициенте преобразования из (1) с учетом (3), (4), получим уравнение, описывающее изменение коэффициентов в разложении амплитуды объектной волны по модам волновода:

i p da 4r- = ^r dz

k ² dn N N

= ^_eE E a 2 m ^Г r , p , m ^{5 T} p 1 ^{( z )eX}P^{[ -} i ^{( e} m -^в r ) ^{z ] + (7)} n 1 dT m = 0 p = 0

k 2 dn N N

+ ~7F E E a 1 nГr,p,n5Tp2(z) eXP[-i(вn -вr)z 1- n dT

¹      n = 0 p = 0

где f n ( x , z ) = f n ( x )exp { - i p n z } - n -я мода волновода; P n - постоянная распространения n -й моды; a jn ( z ) - коэффициенты в разложении амплитуд волн по модам волновода; N – число отсечки.

Меняющиеся в зависимости от поперечной координаты составляющие температуры представим следующим образом:

N

⁵ T 31 ⁽ x . z ) = E ⁵ T p 1 ⁽ z ) ^f р ⁽ x ),

С учетом граничного условия на задней грани волновода a 4 _r ( z = 0) = 0 коэффициенты в разложении амплитуды объектной волны по модам волновода есть

a 4 _r ( z = / ) =

k ² dn

^- i

P _rn ₁ dT

NN

У У Г

/ 4 ц 2 m r, p, m m=0 p=0

x

p = 0

t x f 5Tp 1 (z) exp[-i(pm -pr)z]dz +

NN     £

+ E E alnrr,P,n J 5Tp2(z) eXP[-i(вn -вr)zdz • n=0 p=0          0

В качестве источника сигнальной волны возьмем точечный источник, расположенный на передней грани волновода в точке с координатой x о •

С учетом (8) выражение для функции размытия точки (ФРТ) четырехволнового преобразователя излучения на тепловой нелинейности в волноводе есть

*

^A nmsr = ^в n ^+в m -^в s -^в r =

²'j^P ^ 2

-------1 n + m - s - r I- 2 i a .

x

Для параболического волновода

да

- J f p

-да

d 2 fp,   2 p + 1

---— dx = 22

d x      © 0

= q 2 •

k ² dn

G( x , x ₀) = - i —

⁰ n ₁ dT

N

E

r = 0

fx) NN в E < E a 2 mr r, p, m в r m=0p=0

Подставив (11) в (5) и (6), получим решение уравнений:

£ x J5Tp 1 (z)exp[-i(вm - вr)z]dz +

NN

⁵ T p 1 ^{( x} , ^z ) = EE a 1 n a 3 s ^Г n , s , p X n , s , p ^{( z} ), n = 0 s = 0

N

E

r = 0

NN fr(x) v v Г

/ < E a 1 n ^Г r , p , n ^{в r} m = 0 p = 0

x

NN

⁵ T p 2 ^{( x} , ^z ) = EE a 2 m a 3 s ^Г m , s , p X m , s , p ⁽ z )• m = 0 s = 0

Здесь

a 1

£ x J 5Tp2 (z) exp[-i(вn - вr)z]dz

^л c p ^P q p + ( в , -в * ) 2

где 5 T p 12 ( z ) находится из решения уравнений (5), (6) при граничном условии на коэффициенты в разложении амплитуды сигнальной волны по модам волновода a 3 s ( z = 0) = f k ( x 0 )•

X j , s , p ⁽ z )

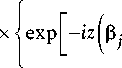
в *

x exp

[- 1 ^£ ( в

) ]

sh [ q_pz ] sh [ q_p £ ] ^X

П ^sh ^[ q p ^{( £ -} z ^{)] в} s ) ]      sh [ q_p £ ]

2. Четырехволновой преобразователь излучения в параболическом волноводе

Рассмотрим двумерный параболический волновод с диэлектрической проницаемостью

s ( x ) = n 2

^{1 -} 2 ^S 2 ( x^x q ) ²

• Модами такого волново-

да являются функции Гаусса – Эрмита [15]:

¹ H n

2 n n ! © 0

( „2 )

exp

-

•

- весовая функция, j = n , m •

Выражения (14) получены при условии неизменности температуры на гранях нелинейного слоя ( 5 T 31 ( x , z = 0) = 5 T 31 ( x , z = £ ) = 0, 5 T 32 ( x , z = 0) = = 5 T ₃₂ ( x , z = £ ) = 0),

Подставив (14) в (9) и проинтегрировав по координате z , получим выражение для ФРТ четырехволнового преобразователя излучения в длинном ( £ Re( A _nmsr ) >>  1, Re( A nmsr ) ^ 0) параболическом волноводе с тепловой нелинейностью в схеме с по-

путными волнами накачки вида

Здесь H_n

–

2    2xq рядка, ©0 = —^

q

ния есть

в _n ~ kn 1 — i ^a

-

xq

функция Эрмита n -го

Для приосевых

по-

мод

постоянная распростране-

. 1 )

n +     •

2 J

С учетом (11) выражение для волновой растрой-ки перепишется следующим образом:

a k ² dn

G₃ ( x , x ) = - i

Л C p p n 1 dT

N

E

r = 0

•w fr(x)

в r

NNN x E EE a 1 na 2 mfn+ m - r(x 0)x m=0 n=0 p=0

^{x {r} n , p , n + m - r ^Г r , p , m

^q p ^{+ ( в} n -^ + m - r ^{) 2}

x

[ 1 - exp ( - 2 a £ )               1

x 1--------------------г-------------------1 x

[       ^{2 a}         sh ( q p ^£ ) [ q p + ( в m -в r ) 2 ]

^x[ q p ^ch ( q p ^£ ) ^- i ^{( в} m ^-в r ) ^sh ( q p ^£ ) ^{+ + [} q p ^ch ( q p ^£ ) ⁺ i ^{( в} m ^-в r ) ^sh ( q p ^£ ) ]^-

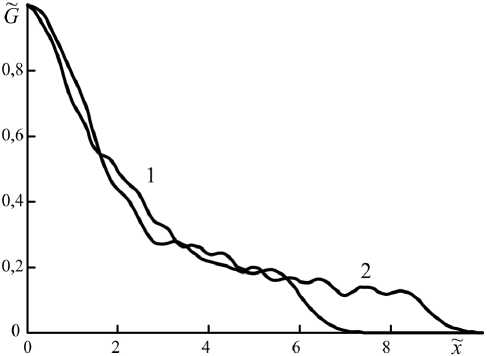
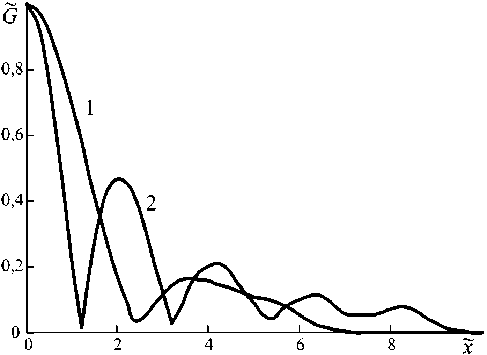
Рис. 1. Зависимость модуля функции размытия точки от поперечной для одной ( а ) и двух ( б) температурных решеток при k £ = 10 5 , 6 = 3 ° , к ш ₀ = 20 (1), к ш ₀ = 40 (2)

Fig. 1. Dependence of the modulus of the point blurring function on the transverse one for one ( a ) and two ( b ) temperature grids at к £ = 10 5 , 6 = 3 ° , к ш ₀ = 20 (1), к ш ₀ = 40 (2)

- q p [exp [- i Л|> m ^-р r ) ] + exp[ ^- i ^{£ (} p _n ^-p n _{+ m} _ r )] ] }

+

+ Г

m , p , n + m - r

г „ r , P , n

q ^{2 + ( в} m ^-в П + m - r ^{) 2}

[ 1 - exp ( - 2 a £ )               1

x 1x

[       ^{2 a}         sh ( q p £ ) [ q P + ( P n -P r ) ² J

^x[ q p ch ( q p ^£ ) ^- i ^{( e} n ^e r ) sh ( q p ^£ ) ⁺

^{+ [} q p ch ( q p ' ) ⁺ i ^{( e} n ^e r ) sh ( q p ' ) ]^-

^- q p ^[exP ^[- i 'Ф n ^-P r ) J ^{+ ex}P^{[ -} i 'Ф m P n + m - r ^{)] ]} } } -

При выводе выражения (15) учитывали связь между номерами мод взаимодействующих волн r = n + m - s .

3. Обсуждение результатов

На рис. 1, а , б приведены нормированные на максимальное значение ( G 1 _max) характерные графики зависимостей модуля ФРТ ( G = G 1/ G _{l max}) от нормированной поперечной координаты ( x = x4% Ду) при условии записи в нелинейной среде одной (рис. 1, а ) и двух температурных решеток (рис. 1, б ). При расчете ФРТ считалось а £ ^ 1, использовались приосевые моды волновода, количество которых определялось из условия

N 1 =

0,1( к ю ₀ ) ²

.

В качестве волн накачки рас

сматривались плоские волны, падающие на переднюю грань волновода под углами 6 1 и 0 2 соответственно: ^ 1 ( x,z = 0) = exp( - ikx sin 6 1 ), A 2 ( x , z = 0) = = exp( - ikx sin 6 2 ).

При записи в волноводе одной или двух температурных решеток и условии, что волны накачки падают на переднюю грань волновода под равными углами ( 6 1 =-6 2 = 6 ) , модуль ФРТ, расположенной на оси волновода, обладает симметрией относительно поперечной координаты (| G 1 ( x , x 0 = ⁰ )| = G 1 ( - x , x 0 = ⁰ )|) .

При записи в волноводе одной температурной решетки, например первой волной накачки и сигнальной волной, и условии, что вторая волна накачки падает на переднюю грань волновода под углом, равным по величине углу падения первой волны накачки, с ростом поперечной координаты, наблюдается уменьшение с небольшими осцилляциями модуля ФРТ (рис. 1, а ). В этом случае для характеристики качества преобразования излучения введем полуширину модуля функции размытия точки A x , определяемую из решения уравнения ^G 1 ( x = ^A x , x 0 = ⁰ ) = 0 5 G 1,max .                     (16)

С увеличением угла падения волн накачки на переднюю грань волновода полуширина (рис. 2, кривая 1), максимальное значение (рис. 2, кривая 2) модуля ФРТ монотонно уменьшаются.

В зависимости от поперечной координаты фаза ФРТ на ее удвоенной полуширине меняется по закону, близкому к линейному. При этом изменение фазы ( ф ( x , x 0 )) функции размытия точки на полуширине модуля ФРТ ( Аф = ф ( x = A x , x 0 = 0) -- ф ( x = 0, x 0 = 0)) с ростом угла 6 увеличивается Аф = р6 .

Здесь Р - коэффициент пропорциональности, зависящий от параметров волновода, значения волнового числа.

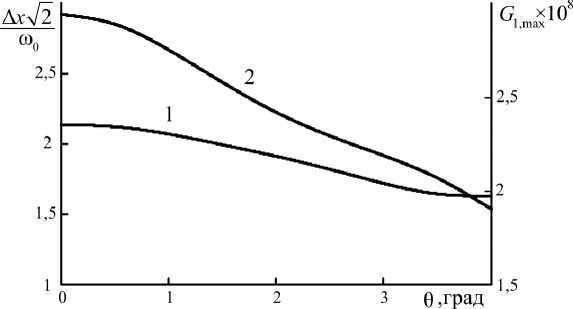
Рис. 2. Зависимость полуширины (1) и максимального значения (2) модуля функции размытия точки от угла падения волн накачки для случая одной тепловой решетки при k t = 10 5 , к ш ₀ = 20

Рис. 2. Dependence of the half-width (1) and maximum value (2) of the modulus of the point spreading function on the angle of incidence of pump waves for the case of one thermal grating at к t = 10 5 , к ш ₀ = 20

При к « о = 20, к t = 10 5 увеличение угла падения волн накачки от нуля до 4 ° приводит к уменьшению максимального значения модуля ФРТ в 1,8 раза, изменению полуширины модуля ФРТ от 1,51 ® o до 1,15 ® o . Коэффициент пропорциональности между изменением фазы и углом падения волн накачки с точностью 5 % равен в = 0,103 л ра-диан/градус.

Увеличение поперечных размеров волновода слабо влияет на нормированную полуширину модуля ФРТ. Наблюдается увеличение энергии, сосредоточенной в «хвостах» ФРТ.

Если вторая волна накачки падает на переднюю грань волновода под углом, отличным от угла падения первой волны накачки, то симметрия модуля ФРТ относительно поперечной координаты нарушается. В этом случае для характеристики качества преобразования изображения введем ширину модуля ФРТ:

Ах 1 = x 1 - x2|, где значения поперечных координат x12 определяются из решения уравнения

G 1 ( х = Х 1,2 , х о ) = 0,⁵ G 1, _max. (17)

При фиксированном угле падении первой волны накачки, например 91 = 3° и к too = 20, к t = 105, изменение угла падения второй волны в диапазоне от -4° до 4° приводит к изменению максимального значения модуля ФРТ на 28 %, изменению ширины модуля ФРТ в пределах от 2,39too до 3, О2®о. Минимальное значение ширины модуля ФРТ наблюдается при условии, что угол падения второй волны накачки 92 ®-91. Этот результат качественно согласуется с характером изменения ширины модуля ФРТ четырехволнового преобра- зователя в схеме с попутными волнами накачки от угла падения второй волны накачки в неограниченной по поперечным размерам среде с тепловой нелинейностью.

Если в волноводе записываются две температурные решетки, то в результате дифракции волн накачки на этих решетках возникают две объектные волны, интерференция которых приводит к появлению «тонкой» структуры ФРТ (рис. 1, б ). Приближенное выражение для числа периодов на удвоенной ширине модуля ФРТ может быть найдено путем деления на л/4 изменения фазы на полуширине модуля ФРТ. Ширина огибающей модуля ФРТ по-прежнему, как и при записи в волноводе одной температурной решетки, определяется поперечным размером волновода, а период «тонкой» структуры – углом падения волн накачки на переднюю грань волновода. Диффузия тепла вдоль оси X приводит к небольшому сужению огибающей модуля ФРТ четырехволнового преобразователя на тепловой нелинейности по сравнению с огибающей модуля ФРТ четырехволнового преобразователя на керровской нелинейности. Так, при к to o = 40 и 9 ^ 0 полуширина модуля ФРТ четырехволнового преобразователя на керровской нелинейности составляет 2, О7 « о [14], а на тепловой нелинейности - 2, 14 « о .

Заключение

Для вырожденного четырехволнового преобразователя излучения в схеме с попутными волнами накачки в волноводе с тепловой нелинейностью значение ширины модуля ФРТ, как и для четырехволнового преобразователя излучения в волноводе с керровской нелинейностью, определяется в основном поперечными размерами волновода.

При записи в волноводе одной температурной решетки и θ1= -θ2 увеличение угла падения волн накачки уменьшает как величину максимального значения, так и полуширину модуля ФРТ. При записи в волноводе двух температурных решеток наблюдается «тонкая» структура ФРТ, период которой с увеличением угла падения волн накачки на переднюю грань волновода уменьшается.