Четырехволновой преобразователь излучения на тепловой нелинейности при квазиперпендикулярной геометрии взаимодействия

Для определения точности обращения волнового фронта (ОВФ) четырехволновым преобразователем излучения необходимо знать соответствие между комплексной амплитудой падающей (сигнальной) волны и комплексной амплитудой отраженной (объектной) волны. Знание такого соответствия позволяет решить вопрос о возможности использования четырехволнового преобразователя излучения для компенсации фазовых искажений, вносимых в излучение оп-тически-неоднородной средой [1; 2].

Одним из наиболее распространенных методов определения точности преобразования излучения при четырехволновом взаимодействии является метод, основанный на построении и анализе функции размытия точки (ФРТ) четырехволнового преобразователя. Критерием точности ОВФ выступает полуширина модуля ФРТ, определяющая разрешающую способность четырехволнового преобразователя [3]. С помощью метода ФРТ была проанализирована точность ОВФ четырехволновым преобразователем на керровской, тепловой нелинейностях в схеме квазикол-линеарного взаимодействия [4–6].

Еще одной перспективной схемой четырехволнового взаимодействия является схема ква-зиперпендикулярного взаимодействия, когда угол между волнами накачки и сигнальной волной близок к 90 градусам [7]. В этой схеме сравнительно просто за счет многократного пропускания сигнальной волны через область нелинейного взаимодействия можно существенно увеличить длину взаимодействия, а значит, и коэффициент отражения четырехволнового преобразователя излучения. При этом снимается проблема, существующая при квазиколлинеар-ном четырехволновом взаимодействии пространственного разделения волны с ОВФ и волны накачки. Подробный анализ пространственных характеристик вырожденного четырехволнового преобразователя в схеме квазиперпендикуляр-ного взаимодействия на керровской нелинейности проводился в работах [8; 9]. Показано, что разрешающая способность четырехволнового преобразователя на керровской нелинейности в схеме квазиперпендикулярного взаимодействия больше разрешающей способности четырехволнового преобразователя в схеме квазиколлине-арного взаимодействия.

Представляется актуальным исследование точности преобразования излучения четырехволновым преобразователем на тепловой нелинейности в схеме квазиперпендикулярного взаимодействия.

1. Вывод выражения для ФРТ

На рис. 1 представлена квазиперпендикуляр-ная схема четырехволнового взаимодействия. Две волны накачки с комплексными амплиту-

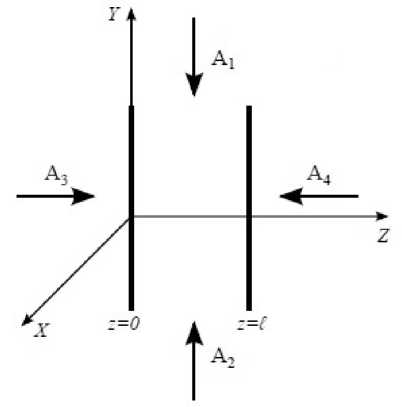
Рис. 1. Схема квазиперпендикулярной геометрии четырехволнового взаимодействия

дами ^A 1 и A ₂ распространяются навстречу друг другу вдоль оси Y. Сигнальная и объектная волны с комплексными амплитудами A ₃ и A ₄ распространяются вдоль оси Z. Четырехволновое взаимодействие рассматривается в нелинейном слое, расположенном между плоскостями z = 0 и z = / .

Исходное уравнение Гельмгольца, описывающее четырехволновое взаимодействие в нелинейной среде, есть

• ¹    = ¹ 0 ⁺ A i A 3 ⁺ A i A 3 ⁺ A 2 A 3 ⁺ A 2 A 3 .

Здесь I о = A i A 3 + A 2 A 3 .

В соответствии с выражением для интенсивности изменение температуры можно представить в виде суммы медленно ( 5 T 0 ) и быстро ( 5 T 3i , 5 T 32 ) меняющихся в зависимости от координат составляющих:

• 5    T = 5 To + 5 T3i + 5 T32 + 5 T3i + 5 T32.

Для упрощения последующих расчетов будем считать, что в нелинейной среде записывается только одна решетка 5 T 3i . Такой случай экспериментально реализуется, например, когда вторая волна накачки некогерентна по отношению к первой волне накачки и сигнальной волне.

С учетом сделанных приближений уравнение Гельмгольца (1) разбивается на четыре уравнения:

V2

+ к2

j = i,3,

+ к ²

V2 + k

:2 I 1

2dn5T I-nо dT J

2ikа ^х

х( A + A *) = 0.

Здесь A = Z A ., а - коэффициент поглощения, j = 1 j

5 T — изменение температуры, обусловленное

выделением тепла при поглощении излучения, n ₀ – среднее значение показателя преломления, к = to n о / c — волновое число.

Уравнение (1) дополняется уравнением Пуас-

сона

V25 T + -а— = 0,                          (2)

Л cP V где Л — температуропроводность, Ср — удельная теплоемкость, V — объемная плотность ве-

щества.

Будем рассматривать четырехволновое взаимодействие в приближении заданного поля по волнам накачки (| A i 21 >>  A 3 4) ) при условии, что коэффициент отражения небольшой (| A 4 2 <<  A 3 2 ).

Выражение для интенсивности взаимодей-

ствующих волн имеет вид

2_ f dn ^ dT J

2 f dn ) dT J

2 ^{k 2} f dn )

+          5 T Ao = 0,

31 2

n 0 A dT J

- 2ikа I Aj = 0,

- 2 ik а IA4 +

а уравнение Пуассона (2) разбивается на два

уравнения:

V 2 5 T_o + -^ I ⁰- = 0, ⁰    Л С р v    ’

V25 T3! + а a1 a3 = 0.

³ⁱ    Л С р v

Пусть первая волна накачки плоская и распространяется строго вдоль оси Y :

A i ( r ) = A 1 ( y ) exp ( iky ) .

Вторую волну накачки, сигнальную и объектную волны разложим по плоским волнам:

да да

A 2 ( r ) = j J A 2 ( ^K 2 x ’ ^K 2 z ’ У ) ^X

-да -да

^X exp ( ^- i ^K 2 x x ^- i ^K 2 z z ^- i^k 2y y ) d ^K 2 x d ^K 2 z ,

да да

A 3,4 ⁽ r ) = J J AA 3,4 ( ^K 3,4 x , ^K 3,4 y , ^z ) ^X

-да -да

^X exp ( ^- i ^K 3,4 x x ^- i ^K 3,4 y y ^- i^k 3,4 z z ) d ^K 3,4 x d ^K 3,4 y .

Здесь j a 234 — пространственные спектры второй волны накачки, сигнальной и объектной

волн, ^к 2,з,4 x , ^к 2 z , К з,4 у и k 2y , k 34z ^- поперечные и продольные составляющие волновых векторов второй волны накачки, сигнальной и объектной волн / < 2 3 4 , r { x , у, z } — радиус-вектор.

В параксиальном приближении

да да

^X J J d ^к 3 x d ^к 3 y A 30 ^{( к} 3 x , ^к 3 у ) ^х

-да -да х exP [гк3xx + гк3уУ + гк3zz] — 0.

,   _ V ^К 2 x + ^К 2 z

— к,

2 y             2 k ,

k 3,4 z

± к +

22 ^к 3,4 x ^{+ к} 3,4 у

2 k

Предположим, что набегом фазы вследствие самовоздействия первой волны накачки можно пренебречь

В приближении медленно меняющихся амплитуд уравнения, описывающие изменение амплитуды первой волны накачки и пространственного спектра второй волны накачки вдоль оси Y , есть

y

[^ kdn j6 Т 0 ( У 1 ) dy 1 <<  1, ikdn 6 Т 0 _{ << 11

^ n 0 dT                  n 0 dT        J

Тогда уравнение (10) перепишется следующим образом:

/-V dA 1,2 dy

ik dn n0 dT

6Т0 + а

/-V

A 1,2 ^— °.

V 2 5 T 31

+--«A! n exp [ гку + а(у - z)] хЛ Cp v   1

При выполнении граничных условий

A 1 ^{( у — 0 ) —} A 10 ,

A 2 ^{( у —} 0, ^к 2 x , ^к 2 z ) ^— A 20 ^{( к} 2 x , ^к 2 z )

да да

^X J J ^{d к} 3 x d ^к 3 у A 30 ^{( к} 3 x , ^к 3 у ) ^х

-да -да х exP [гк3xx + гк3уУ + гк3zz] — 0.

и условия, что интенсивность первой волны накачки намного больше интенсивности второй волны накачки, решения уравнений (6) имеют

Быстро осциллирующую составляющую температуры разложим по гармоническим решеткам

вид

A 1 ( У ) ^— A 10 exP [ C ⁽ У ) ] ,

A 2 ( У ) ^— A 20 exP [ ^- C ⁽ У ) ] .

Здесь

C ( у ) ^— ikdn f ^{5 Т} 0 ( У 1 ) ^dУ 1 ^{+ а} У .

n ₀ dT ₀

Уравнение, описывающее изменение странственного спектра сигнальной волны,

проесть

—W dA 3

dz

ik dn n0 dT

570 + а

—W

A 3 — 0.

При выполнении граничного условия А 3 ( к з _x , к з у , z — 0) — A 30^3 _x , к з у ) решение этого уравнения имеет вид

—W

A 3 ^{( к} 3 x , ^к 3 у , ^z ) ^—

^— A 30 ^{( к} 3 x , ^к 3 у ^)exP

ik dn n ₀ dT

5 70

-

а

z

— 0.

С учетом (7), (9) уравнение для быстро изменяющейся составляющей температуры примет вид

V25Т31 + -1- аA10 exp [гку + C(у)] х Л ср v

х exp

ik dn n ₀ dT

5 Т0

-

а

z

х

да да

^{5 Т} 31 ( r ) ^{— ех}Р^{( а} У ) J J ^{5 Т} 31 ( ^к Tx , ^к Ту , ^z ) ^х

-да -да                        ()

^х exp ( ^{- г к} Tx ^{x - г к} Ту У ) ^{d к} Tx ^{d к} Ту ,

где 5 Т 31 — пространственный спектр решетки.

После подстановки (12) в уравнение (11) получим

I ^1

I dz ²

(к Tx )2 + (к Ту

\ 2

+ г а) ^ 5 Т31 +

*

^а A 10 A 30 exp [ ^{-а z + гк} 3z z ] +-- — 0.

л cpv

Уравнение (13) записано при условии, что

^к Tx ^{— -к} 3 x ,    ^к Ту

^-к 3 у ^- k .

Уравнение (13) необходимо дополнить граничными условиями на изменение температуры

⁵ ^ 31 ( ^к Tx , ^к Ту , ^{z — 0} ) ^—

^{— 5}^ ^ 31 ( ^к Tx , ^к Ту , ^{z —} ^ ) ^— 0.

Решение (13) с учетом (14) есть

⁵ ^ 31 ( ^к Tx , ^к Ту , ^z ) ^— в

f

-

_ Jх кТ [2sh(i<Т1)

х {exp(-icтz) [exp^т 1) - exp(-Pl)]} +

⁺ 9 й¹    { exP(^, К T z ) [ exp( -₽ 1 ) - exp( -!< т 1 ) ] } -

2 sh ( к т 1 )

- exp( -P z ) } .

Здесь f = [«A10A*0(к3x, Кзy)]/ЛCpV , к T = (к Tx )2 + (к Ty + i а)2,

В качестве второй волны накачки возьмем волну, расходящуюся в направлении оси X по

гауссову закону, и не расходящуюся в направлении оси Z

в = a - ik3 z .

С учетом (5), (12) уравнение для амплитуды объектной волны перепишется следующим об-

^А 20 ^{( К} 2 x , ^К 2 z ) = exp

-

2 1 ^К 2 x

К 02 J

5 ( К 2 z ).

разом:

да да dA        ik dn

4 - aA4 =            А2о5T31 х dz         n0 dT

-да -да х exp [i(k4z - К2z)z] dК2xdК2z.

При выводе уравнения (16) считали, что к4x = КTx + К2x> к4y = КTy + k2y•

Уравнение (17) необходимо дополнить граничным условием

A 4 ( К 4 x , К 4 y , / ) = 0.

Проинтегрировав по координате z правую и левую части уравнения (16), получим пространственный спектр объектной волны на передней грани нелинейного слоя в виде

Здесь К 0 — параметр, определяющий ширину пространственного спектра волны накачки. Выбор пространственного спектра второй волны накачки в виде (19) обусловлен тем, что учет расходимости в направлении оси Z , согласно соотношениям К 4 _x = К 2 _x - К 3 _x и К 4 y = -К 3 y - ( К 2 _x + К 2 _z ) / 2 k , оказывает существенно меньшее влияние на вид ФРТ четырехволнового преобразователя, чем учет расходимости волны накачки в направлении оси X . Тогда выражение для функции размытия точки четырехволнового преобразователя на тепловой нелинейности с точностью до постоянного мно-

жителя примет вид

/ да да

A 4 ( К 4 x , К 4 y , z = 0) = - nkdT J J J 5 T 31 A V 20 X ⁰       0 -да -да

да да да

G ( x , y , z 3 , z 4 ) = - J J J

d К 2 _x d К 4 _x d К 4 y х

-да

-да

-да

х exp [ i ( k 4 z - К 2 _z ) z - a z ] dzd К 2 _x d К 2 _z .

х exp

J  К2 x I 1

^*    ^^^^^^^  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^    ^^  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^s

[ (9k)2 J в2 - КT

exp^ t / ) - exp( -в / ) 2 sh ( К t / )

х

С учетом (15) выражение для пространственного спектра объектной волны (17) примет вид

J exp [ (-i«7’ + ik -a ) / ] - 1 1 х <---- —^---z^v -----^j---1 +

^      (-к t + ik 4 z - a )      J

ik a dn *

A 4 ^{( к} 4 x , ^К 4 y , ^z = ⁰⁾ =   ------ “^A 10 A 30

Л c p v n 0 dT

х

да да

1     J exp(i c_TZ ) - exp(^ / )

х A               T           х

J J ²⁰ в ² - К 2 [        2 sh ( К _T / )

-да -да             T j exp [(-кt + ikz - К2z) - a)/] -11

^{( -К} T + i ^{( k} 4 z

-

^К 2 z ) ^{- a )}

exp( -в / ) - ехр( -К t / )

2 sh ( К _T / )

J exp [ ( К t + i ( k 4 _z - К 2 _z ) - a ) / ] - 1 1

( К t + i ( k 4 z

-

^К 2 z ) ^{- a )}

+

exp [(-в + i(k4z - К2z) - a)/] - 1

в - i ( k 4 z - К 2 z ) + a

d К 2 x d К 2 z .

В качестве сигнальной волны рассмотрим волну от точечного источника, расположенного на расстоянии z ₃ от передней грани нелинейного слоя (плоскость фокусировки сигнальной волны). Объектную волну будем рассматривать в плоскости, расположенной на расстоянии z ₄ от передней грани нелинейного слоя (плоскость фокусировки объектной волны).

exp( -в / ) - exp( -i< t / )

2 sh ( К t / )

J exp [ (i c t + ik 4 _z - a ) / ] - 1 [       (i < t + ik 4 z - a )

exp [ ( -в + ik 4 _z - a ) / ] - 1 1

в - ik_{4 z} + a      J

х exp( i — z 4

К

^- i T3 ^z 3 ^- i ^К 4 x ^{x -} i ^К 4 y y ).

Здесь ^К 3,4 = ^К 3,4 x + ^К 3,4 y , ⁹ = ^к о / ^k .

2. Обсуждение результатов

Численный анализ выражения (20) проводился при условии жесткой фокусировки второй волны накачки (0.8 <  Ь // <  20, b = 4 k / к 0 — конфокальный параметр). В качестве количественной меры точности обращения волнового фронта использовалась полуширина модуля ФРТ [10].

На рис. 2 и рис. 3 при z 3 = z 4 приведены зависимости полуширины модуля ФРТ в плоскости XY ( A x ) от расходимости второй волны накачки, положения плоскостей фокусировки сигналь-

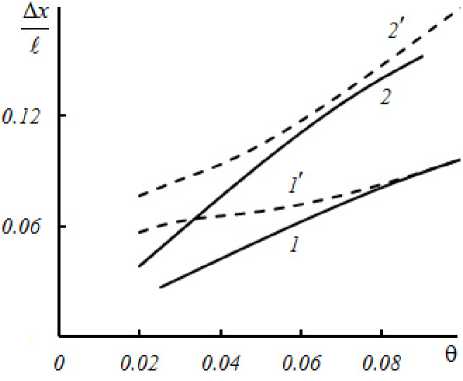
Рис. 2. Зависимость полуширины модуля ФРТ от расходимости второй волны накачки при квазиперпендикулярной (1, 2) и квазиколлинеарной (1’, 2’) геометриях взаимодействия при k £ = 500, а £ = 1, z 3 = £ (1, 1’), z 3 = 2 £ (2, 2’)

ной и объектной волн. На этих же рисунках для сравнения приведены аналогичные зависимости полуширины модуля ФРТ при квазиколлинеар-ной геометрии взаимодействия.

Выражение для ФРТ при квазиколлинеар-ной геометрии совпадает с выражением (20) при замене следующих параметров: к т на к T = ^( к Tx )² + ( к Tу )², Р на Р'= ^{2 а} + ( к | x + к | у )/ / 2 к , + к т + ik 4 z - а на + к T - ip , + Р ± ik 4 z + а на + Р + ip , где , ^K Tx = К Tx , ^K Ty = —К д у = К 4 у , p = ^{( к} 2 x ^{- к} 4 x ^{- к} 4 у ) / ^2к .

Характер изменения полуширины модуля ФРТ в зависимости от положения плоскости фокусировки сигнальной волны, расходимости волны накачки как в схеме квазиколлинеарного, так и в схеме квазиперпендикулярного взаимодействий совпадают. Увеличение расходимости волн накачки, расстояния от передней грани нелинейного слоя до плоскости фокусировки сигнальной волны приводит к увеличению полуширины модуля ФРТ.

Полуширина модуля ФРТ при квазиперпен-дикулярной геометрии взаимодействия меньше, чем полуширина модуля ФРТ при квазиколли-неарной геометрии. Точность ОВФ четырехволновым преобразователем излучения на тепловой нелинейности при квазиперпендикулярной геометрии взаимодействия выше, чем при квази-коллинеарной геометрии взаимодействия.

Учет расходимости волн накачки ограничивает область нелинейного взаимодействия. При ка-зиперпендикулярной геометрии взаимодействия в параксиальном приближении характеристики тепловых решеток слабо меняются при изменении направления распространения сигнальной

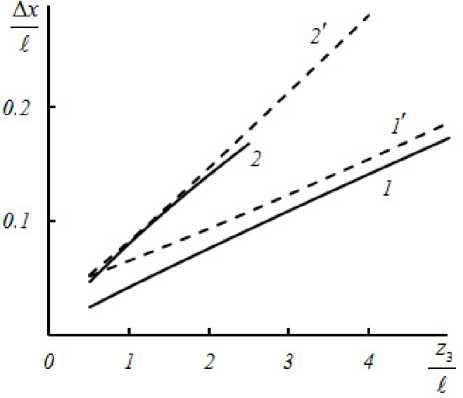
Рис. 3. Зависимость полуширины модуля ФРТ от положения плоскости фокусировки сигнальной волны при квазиперпен-дикулярной (1, 2) и квазиколлинеарной (1’, 2’) геометриях взаимодействия при к £ = 500, а £ = 1, 6 = 0.04 (1, 1’), 0 = 0.08 (2, 2’)

волны. Поэтому для этой схемы взаимодействия основным фактором, влияющим на точность ОВФ, является пространственная структура волн накачки. При увеличении расходимости второй волны накачки ширина области нелинейного взаимодействия уменьшается вдоль оси Х , не меняясь вдоль оси Z . Это объясняет линейную зависимость при 6 <  0.07 ширины модуля ФРТ от расходимости волны накачки (рис. 2).

При квазиколлинеарной геометрии четырехволнового взаимодействия на точность ОВФ влияет прежде всего зависимость амплитуды тепловой решетки от угла между волной накачки и сигнальной волной, а затем размер области взаимодействия. Наличие двух механизмов, уширяющих модуль ФРТ, приводит к существованию пороговой расходимости волны накачки ( ⁶ n ) . При ⁶ < 6 n полуширина модуля ФРТ не зависит от расходимости волны накачки, определяется толщиной нелинейной среды, волновым числом [3]. При 6 > 6 n увеличение расходимости волны накачки приводит к монотонному увеличению полуширины модуля ФРТ.

Зависимость полуширины модуля ФРТ четырехволнового преобразователя излучения при z 3 = z 4 от положения плоскости фокусировки сигнальной волны при квазиперпендикулярной геометрии взаимодействия близка к линейной (рис. 3), что хорошо соответствует модели четырехволнового преобразователя в виде объемной «ОВФ-диафрагмы».

Численный анализ выражения (20) показывает, что в области расходимости второй волны накачки 9 < 0.02 и положения плоскости фокусировки сигнальной волны z3 < 0.5/ ошибка расчета полуширины модуля ФРТ превышает 3 %. Это обусловлено сильной зависимостью получаемых значений полуширины модуля ФРТ от пределов интегрирования при заданных 9 и Z3. Таким образом, на рис. 2, 3 отсутствуют зависимости полуширины от расходимости второй волны накачки и от положения плоскости фокусировки сигнальной волны в пределах указанных областей.

Заключение

Анализ пространственных характеристик четырехволновых преобразователей излучения на тепловой нелинейности показывает, что характер зависимостей полуширины ФРТ от положения плоскости фокусировки сигнальной волны, расходимости волны накачки как в схеме с квазиперпендикулярной, так и в схеме с квазиколлинеарной геометриях взаимодействия сохраняется. В схеме с квазиперпендикулярной геометрией взаимодействия расходимость волны накачки полностью определяет полуширину модуля ФРТ . При учете расходимости волны накачки точность ОВФ четырехволновым преобразователем при квазиперпендикулярной геометрии выше, чем при квазиколлинеарной геометрии.