Четырёхволновое взаимодействие на резонансной и тепловой нелинейностях

Важнейшей характеристикой любого четырёхволнового преобразователя излучения является соответствие межд у комплексными амплитудами падающей (сигнальной) и преобразованной (объектной) волн. Знание такого соответствия позволяет решить вопрос о целесообразности применения четырёхволновых преобразователей в системах нелинейной адаптивной оптики, в системах обработки и преобразования изображения и т. д. [1–3].

Как правило, изучение соответствия межд у комплексными амплитудами сигнальной и объектной волн при четырёхволновом взаимодействии происходит на нелинейности одного типа [4–8]. Учёт нескольких типов нелинейности существ енно усложняет решение поставленной задачи [9–10].

При четырёхволновом взаимодействии в поглощающих средах, например, в средах с резонансной нелинейностью, существенный вклад в объектную волну может быть обусловлен наличием тепловой нелинейности [11, 12]. Поэтому представляет интерес изучение соответствия между комплексными амплитудами сигнальной и объектной волн при наличии как резонансной, так и тепловой нелинейностей.

где 8 T - изменение температуры, обусловленное выделением тепла при поглощении излучения, c p – теплоёмкость, Л - температуропроводность, v -плотность вещества. В случае двухуровневой модели среды а ₀ = N о ₁₂ - начальный коэффициент поглощения, b = ( g ₁₂ + а ₂₁) / 8 ₂₁ - параметр, представляющий собой комбинацию сечений поглощения ( g ₁₂, g ₂₁) и скорости релаксации между энергетическими состояниями резонансной среды ( 8 ₂₁ ) , N - число частиц.

Будем рассматривать четырёхволновое взаимодействие при след ующих условиях:

• 1)    в нелинейной среде распространяются четыре волны;

• 2)    справедливо приближение заданного поля по волнам накачки ;

• 3)    учитывается решётка, возникающая при интерференции первой волны накачки и сигнальной волны.

Изменение температуры можно представить в виде суммы быстро ( 8 T ₃₁ ) и медленно ( 8 T _o ) меняю-

1. Основная часть

Пусть в плоском слое с резонансной и тепловой нелинейностями толщиной l распространяются две волны накачки с комплексными амплитудами A 1 и A 2 и сигнальная волна с амплитудой A 3 . В результате четырёхволнового взаимодействия ®+®-®=® генерируется объектная волна с комплексной амплитудой A 4 .

Исходное скалярное волновое уравнение, описывающее четырёхволновое взаимодействие в нелинейной среде, есть

[ V2 + к1 + — dn 8 T - 2^)(A+A *) = 0.   (1)

(           n ₀ d T 1 + bi J^v ’

Здесь I = AA * , A = ^ A . , к - волновое число, j = 1

щихся в зависимости от координат составляющих

8 T = 8 To +8 T31 + 8 T/1.

С учётом сделанных приближений волновое уравнение (1) примет вид

V2 + к2 + 2k2 dn (8 To +8 T,1 +8 T/1) - n0 dT

^{2 ik a} o 1 1 + bi o L

b ( A 1 A 3 + a ; A 3 ) i + bl O

A = 0.

n 0 – среднее значение показателя преломления.

Уравнение (1) дополняется уравнением Пуассона [13]

V 2 8 T +--- O I -- = o,

Лcp v(1+bi)

Здесь I о = I + I 2 . I j = A j A * , j = 1,2.

Пусть волны накачки плоские:

• ^A 1,2 ( r ) = ^A 1,2 ( z ) exP [ ^{- ik}12 r ] .

Сигнальную и объектную волны разложим плоским волнам

Aj( Г ) =

• = J :Aj ( k j ,z ) exp ( - i k j P - ik j_Z z ) d K. , j = 3,4.

—^

Здесь K j и k_jz - поперечная и продольная ставляющие волнового вектора k_j .

по

со-

Быстро осциллирующую составляющую температуры разложим по гармоническим решёткам ^

8 T ₃₁ ( r ) = i 8 7 331 ( К _t , z ) exp ( - i К _T p ) d К _T .

-^

С учётом приближения медленно меняющихся амплитуд волновое уравнение (1) распадается на систему уравнений вида dA-+AI2k 2118T. ■   a    Li, = 0, j = 1 * 3, dz   kz к n 0d T 0 (1 + bl0) J j

Если интенсивность первой волны нак ачки намного превосходит интенсивность второй волны накачки, то изменение по толщине нелинейной среды интенсивности первой волны накачки описывается след ующим выражением

1 I (z) 7r > 2a0kz In—+ b ( 11 ( z )-110 ) =-^,

I10                                    k1z где I10 = 11 (z = 0).

Сделаем замену

4             I                                        \

dA4    k J ik d1          ao    | ~*8In +■;A4 = dz   k4 z к n „d T   0   (1 + bl0) J 4

-k^- d ^{1 8} 7 31 A2 • exp { ^{- iz} ( ^k 2 z ^{- k} 4 z ) } ⁺ k 4 z n 0 d T

4 4 4

k a ₀bA 1 A 2 A * • exp ( - i A z )

+       k4z (1+bl0 )2       , где A = ( k1 + k2 - k3 - k4) - проекция волновой расстройки на ось Z.

Уравнение Пуассона распадается на два уравнения

V ² 8 T 0 +---- O o I o---- = 0,

Л cp V(1 + bI0)

3A 4 = VAV exp { - C 4 ( z ) } .

Тогда с учётом (7) уравнения, описывающие изменение комплексной амплитуды объектной волны, быстро изменяющейся составляющей температуры по толщине нелинейной среды, имеют вид d^44 = k^20 exp (-C2 (z)+ C2 (l)+ C4 (z)) x

k _{4 z}

^x I ^{- k} d^ ^{8 7} 31 exp { ^- iz ( ^k 2 z ^{- k} 4 z ) } ⁺ к n 0 d T

* ^{a bA}10 A

(1+bl0)2

)exp{-C1 (z)- C3(z)- i^z} , J

d2 dz2

КT I 8 T31 +

^a A 1 A 3 exp { ^{- iz} ( ^k 1 z ^{- k} 3 z ) }

Л cp V(1 + bl0 )2

= 0.

d2 dz2

kt I8 T31 +

*

^ 0^10^30

^Л c p ^V( 1 ^{+ bI} 0 ) 2

X

Системы уравнений (5), (6) записаны при условии равенства нулю проекций волновой расстройки на оси X и Y : К 1 + К ₂ - К ₃ - К ₄ = 0 и при условии, что К 1 - К ₃ = К _T .

Системы уравнений (5), (6) необходимо дополнить граничными условиями:

– на амплитуды взаимодействующих волн

x exp {-iz ( k1 z - k3z )- C1 (z )- C3 (z )} = 0.

Из уравнения (9) след ует, что амплит уд у объектной волны можно представить в виде суммы амплитуд волн, возникающих в результате четырёхволнового взаимодействия соответственно на тепловой и резонансной нелинейностях

4-

4-

4-

4-

4-

A (z = 0 ) = A10,

A4 (К4,z = 0) = A4T (К4,z = 0) + A’R (К4,z =

Здесь

4-

4-

A 2 ⁽ z ^l ) A 20 ,

A3 ( K3 , z = 0) = A30 ( K3 ) , A4 (К4,z = l) = 0;

– на изменение температуры 8 T 0 ( z = 0 ) = 8 T 0 ( z = l ) = 0, 8 T ₃₁ ( z = 0 ) = 8 T ₃₁ ( z = l ) = 0. Граничные условия на изменения записаны при условии неизменности на гранях нелинейного слоя.

Решение первых трёх уравнений есть

A 1,3 ^{( z} ) = A 10,30 ^{exp {- C} 1,3^{( z ) }} , 3A2 ( ^z ) = 3A 20 exp {^- C 2 ^{( z} ) ⁺ C 2 ^{( l} ) } . Здесь

^A 4 T ^{( K} 4 , z ⁰ ) =

——— A ₀ exp{ C ₂ ( l )} x k 4 zn 0 d T ^{20 P{ 2V }}

x i 8 7 31 exp { - iz ( k 2 z - k 4 z ) - C 2 ( z ) + C 4 ( z ) } d z , 0

A4R (K4,z = 0) =

^{k a bA}10 A ^A q ^exp { ^C 2 ( ^l ) } _x

k _{4 z}

z

=д-)=г i I kjz 0 к

ik ² d n

----^{8 T} 0 ^{( z} 1 ^{) +} n ₀ d T

температуры температуры

системы (5)

k a ₀

(1 + bl0 (z1)) J

> dz1 .

l

Xi

exp{-C1 (z)- C2 (z)-C3 (z)+ C4 (z)- iAz}

( 1 + bI 0 ) 2

(12) d z .

На быстро изменяющуюся в пространстве составляющую температуры, а значит, и амп лит уд у волны, возникающей в результате четырёхволнового взаимодействия на тепловой нелинейности, существенное влияние оказывает изменение интенсивности волн накачки, об условленное наличием резонансной нелинейности.

Как след ует из (11), (12) с учётом (6), при четырёхволновом взаимодействии плоских волн в тонкой нелинейной среде основной вклад в объектную волну даёт резонансная нелинейность при условии, что

параметр g = ——---- .    (0 - угол между dT n 0 к Лcp vb sin 0

первой волной накачки и сигнальной волной) намного меньше единицы. Если параметр g ≫ 1 , то основной вклад в объектную волну даёт тепловая нелинейность.

2. Обсуждение результатов

На рис. 1 приведены характерные графики зависимости модулей амплитуд объектной волны от толщины нелинейного слоя, полученны е путём численного анализа выражений (10)–(12) при условии, что вклад тепловой и резонансной нелинейностей сравним.

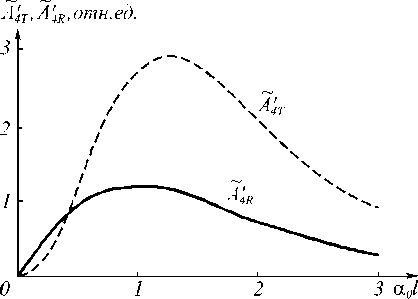
Рис. 1. Зависимость модуля амплитуды объектной волны от толщины нелинейного слоя ( 9 = 3 град, bI 10 = 1)

Графики построены при условии, что волны накачки распространяются строго вдоль оси Z и при след ующих значениях п араметров:

к, а ₀ = 100,

I10     dn vЛcp a0n0 dT

r-J                        r-J

Значения амплитуд A4T и A4R с ростом толщины нелинейного слоя вначале возрастают, а затем уменьшаются. Причём оптимальные толщины нели- нейной среды loptT и loptR , при которых значения ам- плитуд волн A4T и A4R достигают наибольшего зна- чения, различны.

С увеличени ем интенсивности волны накачки происходит уменьшение коэффициента поглощения и, как следствие этого, увеличение оптимальны х толщин l_optT и l_optR (рис. 2).

При этом растёт также и значени е амплитуды объектной волны A 4R , соответствующее 1_optR . Рост значения l_optT приводит вначале к ув еличению, а затем к уменьшению A ’ _Т ( 1_optT ) (рис. 3).

В приближении плоских волн накачки угловая зависимость амплитуды объектной волны, возникающей в результате четырёхволнового взаимодействия на резонансной нелинейности, отсутствует [8]. Амплитуда волны, возникающей в результате четырёхволнового взаимодействия на тепловой нелинейности, с увеличе- нием угла между сигнальной волной и первой волной накачки, уменьшается. Для характеристики угловой зависимости амплитуды A'4Т введём понятие ширины полосы углов (А0), определяемое из соотношения

IA^ (0 = А0)|= 2AТ (0 = о)|

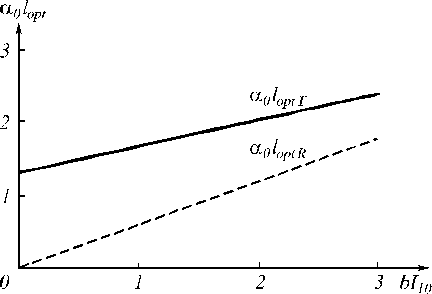
Рис. 2. Зависимость оптимальных толщин от интенсивности волны накачки ( 9 = 1 град)

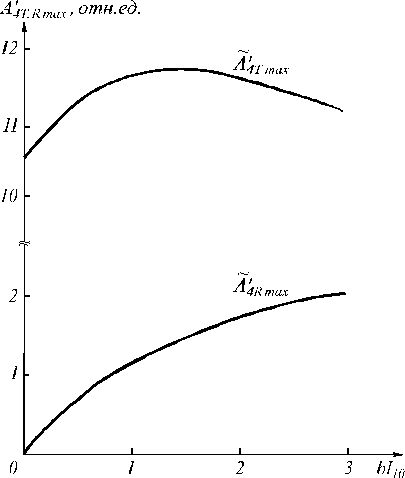
Рис. 3. Зависимость модуля амплитуды объектной волны, соответствующего оптимальной толщине среды, от интенсивности волны накачки ( 9 = 1 град)

Ширина полосы углов, соответствующая оптимальной толщине нелинейной среды А01 = А0( loptT), с увеличени ем интенсивности волны нак ачки монотонно уменьшается (рис. 4).

При фиксированной толщине нелинейной среды ув еличение интенсивности волн накачки слабо влияет на угловую зависимость амплитуды A'_4T . Так, при изменении нормированной интенсивности волны накачки bI ₁₀ в пределах от 0,1 до 3, относительное изменение ширины полосы углов при а ₀ 1 = 0,8 составляет 0,4%, при а ₀ 1 = 4 - 3,6%.

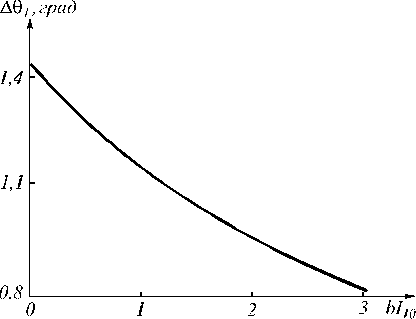
Рис. 4. Зависимость ширины полосы углов, соответствующей оптимальной толщине среды, от интенсивности волны накачки

В рамках параксиального приближения угловой поворот второй волны накачки относительно первой при фиксированной толщине нелинейного слоя не меняет ширину углового спектра волны, возникающей при четырёхволновом взаимодействии на тепловой нелинейности, при этом резко уменьшается ширина углового спектра волны, возникающей при четырёхволновом взаимодействии на резонансной нелинейности. Однако вплоть до значений k / α ₀ <  2000 и α ₀ l <  2 ширина углового спектра волны A ₄ ′ _T меньше ширины углового спектра волны A ₄ ′ _R .

Тот факт, что объектная волна представляет сумму двух волн с различной пространственной селективностью, позволяет использовать четырёхволновой преобразователь с учётом двух типов нелинейности для динамической фильтрации неоднородностей в системе «нелинейная среда – четырёхволновой преобразователь – нелинейная среда». Изменяя интенсивность волны накачки, можно увеличивать долю «резонансной» составляющей волны A ₄ ′ _R и, тем самым, компенсировать мелкие неоднородности или, наоборот, увеличивать долю «тепловой» составляющей волны A ₄ ′ _T и компенсировать крупные неоднородности.

Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы (Государственный контракт № 14.740.11.0063).