Численная аппроксимация конвективного граничного условия для сеток с подвижными узлами

При плавлении, затвердевании и окислении металла, при аварийном замерзании воды в теплопроводах и в системах водоснабжения, при расчете процесса охлаждения и замерзания подвижного фронта теплоносителя во время заполнения пустого трубопровода при пуске в зимних условиях, при промерзании влажного грунта, в том числе и при наличии снежного покрова с переменной толщиной и в других случаях возникает задача расчета температурных полей в областях с переменными во времени границами [1–7]. При конечно-разностном решении такой задачи, как правило, применяют метод ловли границы в узел пространственной сетки [7, 8], что обусловливает необходимость использования при расчетах переменного шага по времени, кроме того, переменным будет и число пространственных узлов. Здесь более предпочтительным может быть метод сеток с подвижными узлами [9–11]. Это позволяет, в частности, избежать изменения количества узлов расчетной сетки и в связи с этим и размерности используемых информационных массивов, а также и шага по времени, что может быть достаточно привлекательным, например, при разработке программного обеспечения. Однако при этом следует иметь в виду, что в любом случае – как при численных расчетах с постоянными размерами шагов по пространственным координатам, так и при переменных размерах таких шагов необходима конечноразностная аппроксимация граничных условий, описывающих особенности теплообмена иссле- дуемого твердого тела с окружающей средой. При этом известно, что решение этой задачи непосредственной заменой производных конечными разностями может привести к большим погрешностям вычислений. Поэтому необходима разработка специальных подходов и решений этого вопроса.

Актуальность исследуемого вопроса

Согласно данным работ [1, 5–7] актуальность задачи расчета температурных полей в областях с переменными во времени границами для настоящего времени весьма значительна, в литературе отмечается недостаточная развитость и обоснованность некоторых подходов и приемов, в частности, метода сеток с подвижными узлами. Поэтому изучение и выявление всех сторон и особенностей метода сеток с подвижными узлами имеет достаточно большое значение.

Постановка задачи исследования

Чаще всего теплообмен на границе описывается граничным условием III рода, которое имеет вид:

-XdN Г=a( t С - t1 г ), (1) где t = t (M, т) - температура тела в точке M в момент времени т ; N - нормаль к границе Г (поверхности тела); X, a - соответственно коэффициенты теплопроводности и теплоотдачи; tС, t Г – соответственно температура окружающей среды и температура поверхности тела (температура тела на границе).

Известно, что уравнение (1) обычно аппроксимируется следующей конечно-разностной схемой:

рез q 1 = ( q 1 + q 1 ^{+ 1} ) J 2, причем нетрудно видеть, что

q1 = a

,к . ,k + 1 t С ⁺ t С

—

к   к + 1

t n ⁺ t n

kk

X kJ n —L =a ( - * — t n ),                     (2)

h

k где tn – температура поверхности тела (в узле n ) в момент времени к-Ат, a tk-1 - температура тела в соседнем узле n -1, удаленном от поверхностного узла на величину шага по пространству h , в тот же момент времени к - Ат; tС - температура среды

Далее, плотность теплового потока теплопроводностью в поверхностном слое тела обозначим соответственно в начале Ат через q k , а в

к + 1

конце - через q 2 , среднее его значение - через q ₂ = ( q^к + q^{к + 1} ) ^2 , причем нетрудно видеть, что

Г/ к q 2 =x |- n

-

2 h^k

k tn —1

к + 1 к + 1

+ t n t n — 1

2 h^{k + 1}

-

.

в момент времени к -Ат ; Ат - размер расчетного

шага по времени. Здесь предполагается, что размер расчетной области по направлению нормали N делится на n частей (шагов h ).

Известно также [12], что аппроксимация граничного условия (1) конечно-разностной схемой (2) дает заметную ошибку при определении темпера-

Здесь h^k и h^{k + 1} - расстояние между узлами расчетной сетки в моменты времени к -Ат и

туры поверхности тела, если a h , — < 1.

X

( к + 1) -Ат соответственно.

Следуя [8, 13–15], примем, что размер контрольного объема (элементарной ячейки) для поверхности равен полуслою и оценим теплосодержание (энтальпию) полуслоя на поверхности в начале и в конце временного шага Ат : c р - к ^ /2 и соответственно c р -^{к + 1} h^{k +1}/ 2. Здесь

В этом случае для повышения точности опре-

деления температуры поверхности и в связи с этим и всего температурного поля тела при расчете методом сеток с постоянным шагом по пространственной координате h можно использовать формулу аппроксимации, предложенную Беком [13]. Согласно [12] формула Бека прошла успешную апробацию в практике вычислений.

Если же для расчета температурного поля используется метод сеток с подвижными узлами [9–11], то, естественно, возникает вопрос: какой вид будет иметь формула, аналогичная формуле Бека, но для сеток с подвижными узлами. В данной работе дается ответ на этот вопрос.

c , р - соответственно удельная теплоемкость и плотность вещества, кроме того, также как и в [13] считалось, что средняя температура полуслоя равна температуре поверхности тела.

Разность между количеством теплоты, подведенным к полуслою на поверхности теплоотдачей, и количеством теплоты, отведенным от него за время Ат теплопроводностью во внутрь тела, со-

гласно закону сохранения энергии представляет запасенное количество теплоты, идущее на изменение теплосодержания (энтальпии) полуслоя. Математически это запишется так:

Теоретическая часть исследования

При выводе формулы аппроксимации в работе [13] использовался достаточно известный прием: для получения разностного решения, хорошо описывающего реальное температурное поле, целесообразно выполнение закона сохранения энергии и для самой разностной схемы [14, 15]. Данный метод часто называют методом конечного контрольного объема [15] или методом теплового баланса для элементарных объемов [8, 14]. Следует заметить, что в отличие от [13] при выводе формулы аппроксимации граничного условия для сеток с подвижными узлами будем использовать усреднение не температур на интервале времени Ат , а плотностей тепловых потоков.

Обозначим плотность теплового потока теплоотдачей в начале интервала времени Ат через q k , к + 1

а в конце - через q1 , среднее его значение - че

Г к +1 /. к +1

( q 1 ^{— q} 2 ) ^-Ат = ^c р| — ^---

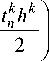
Преобразовывая это уравнение соответствующим образом, получим искомую формулу аппрок-

симации:

, к + 1 t _n

к Г x h^к t n ^k

I а -Ат

Г к      к + 1

—a—4 + a( - к + - к 4 +X t n — ¹ + t n — 1 h^k )   И ^С I h^k   h^k + 1

, к + 1

X

. (7)

+ a+ а - Ат      hk+1

Здесь a – коэффициент температуропроводности.

Заметим также, что в случае, если h^k = h ^{+ 1} = h ,

т. е. если граница раздела сред неподвижна, то из (7) вытекает формула аппроксимации Бека [13], которая в данном случае будет иметь вид:

, к + 1 t _n

. к Г h h n

I а -Ат

ah т

—

, la hi к        к i +v( tС+tС+1)+tn—1

X

+1

k + 1 n — 1

h2 ah , ---+— + 1 а -Ат X

. (8)

Апробация формулы аппроксимации

В работах [12, 13] показано, что предложенная Беком формула аппроксимации конвективного граничного условия совместно с известными методами [7, 14, 16] конечно-разностной замены дифференциального уравнения теплопроводности обеспечивает достаточно точное описание нагрева (охлаждения) массивных тел. Это в известной мере подтверждает ее адекватность реальным физическим процессам.

На адекватность полученной для сеток с подвижными узлами формулы аппроксимации (7), учитывая вышеотмеченное, в определенной мере указывает тот факт, что при h k = h k ^{+ 1} из нее частным случаем получается формула аппроксимации Бека. Кроме того, с целью апробации формулы (7) применялся следующий прием: сравнивались результаты расчета нагрева стальной пластины без учета окисления и с учетом его, но при предположении, что металл сразу после окисления осыпается и не влияет на теплообмен, т. е. окисление приводит только к уменьшению толщины пластины. Такое сравнение обусловлено тем, что в литературе отсутствуют точные данные о распределении температуры в окалине и металле с учетом переноса теплоты через поверхностный слой окисленного металла. Кроме того, натурный эксперимент по определению, например, температуры подвижной границы весьма затруднителен, в частности, из-за того, что в этом случае необходим подвижный датчик температуры.

При выполнении расчетов в первом случае граничное условие (1) аппроксимировалось формулой Бэка, а во втором – формулой (7). Уравнение теплопроводности всех случаях аппроксимировалось неявной разностной схемой, которая решалась методом прогонки. В случае учета окисления металла использовалась схема с подвижными узлами приведенная в [10].

Совершенно ясно, что уменьшение геометрических размеров (толщины) пластины из-за окисления при расчетах должно приводить к лучшему прогреву металла. Однако температурные распределения в обоих случаях должны незначительно отличаться друг от друга вследствие относительно незначительного уменьшения толщины стальной пластины в результате окисления металла. Это и подтверждается при сравнении результатов расчета.

Представляет также интерес сравнение результатов расчета температурных полей при различных способах аппроксимации конвективного граничного условия для сеток с постоянным шагом по пространству: формулой (2), полученной простой заменой производной конечной разностью, и формулой Бека.

В таблице приведены результаты расчетов симметричного нагрева стальной пластины толщиной 0,1м при a = 0,02 м²/ч , Х = 30,24 Вт/(м -° С) , а = 348,9 Вт/(м² -° С). При этом полагалось, что в начальный момент времени температура во всех точках по толщине пластины одинакова и равна 700 °C (так называемый горячий посад), температура греющей среды t _С = 1300 ° C, а окисление металла описывается следующим соотношением: д hoк /Т = - 39,4/ h_Oк ( т ) . exp { - 7580/ [ t нм ( т ) + 273 ] } х х 10 — 4 ,м/ч, полученным аппроксимацией экспериментальных данных. Здесь h _ОК – толщина окалины, а t _НМ – температура поверхности неокис-ленного металла (в реальных условиях под слоем окалины).

В таблице t _{ПМ i} и t _{Ц i} – значения температур поверхности и центра нагреваемой пластины при следующих условиях: i =1 - нагрев без учета окисления при аппроксимации граничного условия формулой (2); i =2 - то же самое, но при аппроксимации граничного условия формулой Бека; i = 3 - нагрев с учетом окисления, приводящего только к уменьшению толщины пластины (считается, что окисленный металл сразу осыпается), и аппроксимации граничного условия формулой (7).

Температура поверхности и центра пластины

Время, мин	Температура,°C						Половина толщины неокисленного металла, м
	t ПМ1	t ПМ2	t ПМ3	t Ц1	t Ц2	t Ц3
0	700	700	700	700	700	700	0,05
3	903,6	903,53	904,76	777,73	780,46	783,55	0,04897
6	976,77	967,26	969,27	870,46	867,48	872,20	0,04892
9	1035,45	1024,55	1027,67	948,22	941,22	946,99	0,04884
12	1083,4	1071,54	1075,43	1011,98	1002,45	1008,97	0,04872
15	1122,67	1110,54	1115,02	1064,19	1053,24	1060,29	0,04858
18	1154,81	1142,88	1147,79	1106,94	1095,36	1102,78	0,04842
21	1181,13	1169,70	1174,92	1141,93	1130,29	1137,94	0,04825
24	1202,68	1191,97	1197,36	1170,58	1159,26	1167,02	0,04807
27	1220,32	1210,38	1215,92	1194,04	1183,28	1191,04	0,04788
30	1234,76	1225,68	1231,24	1213,25	1203,20	1210,87	0,04770

Значения половины толщины пластины, приведенные в таблице, относятся только к случаю i = 3 .

Как видно из таблицы, расхождение значений t _ПМ2 и t _ПМ3 , а также t _Ц2 и t _Ц3 составляет относительно незначительную величину, что позволяет сделать вывод о том, что формула (7) обеспечивает удовлетворительное описание процесса и может быть рекомендована для использования при расчете температурных полей в областях с подвижными границами.

Практическая значимость результатов

Полученная формула аппроксимации конвективного граничного условия для сеток с подвижными узлами, как нам представляется, может быть неким дополнением к теоретическим основам используемого в практике вычислений температурных полей в областях с переменными границами метода сеток с подвижными узлами.

Выводы

Рассмотрена задача аппроксимации конвективного граничного условия для сеток с подвижными узлами. Используя закон сохранения энергии для элементарной ячейки у поверхности тела, получили формулу численной аппроксимации граничного условия, аналогичную известной в литературе формуле Бека. Формула аппроксимации может быть использована для повышения точности расчета температурного поля тела с подвижными границами.