Численная аппроксимация линий тока методом Галёркина

Постановка задачи

Для расчёта течений в озерах, бассейнах и других водоёмах при-меняется упрощенная модель с целью начальной оценки циркуляции, которая затем может быть сопоставлена с результатами применения полных уравнений количества движения в мелководных бассейнах [4]. Линеаризованные уравнения таких течений получаются из уравнений количества движения, если отбросить инерционные члены, т.е.

-/дх+ргА^+^-г,!^ О, /»,+pg^+(r,|.-r,|J= О; (1) сх                                   су ^{15     19}

и рассмотреть стационарное уравнение неразрывности:

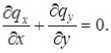
Здесь f – параметр Кориолиса; q_x и q_y – компоненты средних значений массового расхода; ρ – плотность жидкости; h – расстояние от оси x до дна, а η << h – возвышение свободной поверхности; τ_x|_S , τ_y|_S – составляющие внутреннего напряжения трения на поверхности, а τ_x|_b , τ_y|_b – на дне.

Величины τ|_S в уравнениях (1) зависят от ветровых напряжений. Примем, что напряжение трения на дне прямо пропорционально среднему значению массового расхода:

rzL=^x- ^L=;^ (2)

Предположим также, что наклон дна мал и введем функцию тока ψ :

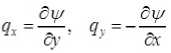
Таким образом, из (1)-(3) получим уравнение Пуассона относительно функции тока следующего вида

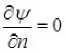
Здесь TV = 3^7^ – величина, зависящая от ветрового воздействия; γ – коэффициент ветрового напряжения.

Граничные условия для уравнения (4) имеют вид:

на береговых границах;

на входе в водоём.

Уравнение (4) вместе с указанными граничными условиями (5), (6) допускает вариационную формулировку и применение метода взвешенных невязок.

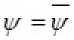
Уравнения в безразмерных переменных

Для численного решения уравнения (4) удобно перейти к безразмерным переменным по формулам

х = Lxx . у =     ; qx = Qxqx, qx = Qx qv;

Fj = Тхт°. Г- = T-; r.. ^ = Ty/C.

Здесь переменные с верхним индексом " b " являются безразмерными; L_x(L_y), Q_x(Q_y), T_x(T_y), Ψ – масштабы длины, массового расхода, внутреннего напряжения трения и функции тока соответственно.

Подставляя соотношения (7) в (2), (3) и приравнивая масштабы в левых и правых частях этих равенств, получим следующие связи между введёнными масштабами

Y Y

tx = tQv t. = )Q-, qx=—, Qx = —        (8)

С учётом выражений (8) уравнение Пуассона (4) примет наиболее простой вид, если

= L . В этом

слу-

Равенства (9) будут верными, если L_x = L_y чае уравнение Пуассона (4) примет вид

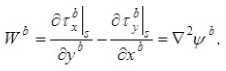
Метод взвешенных невязок

Рассмотрим прямоугольное озеро П = {( x, у ) | a < х < b, c } (здесь и далее верхние индексы у безразмерных переменных опущены), которое подвержено воздействию ветра так, что W = Ax + By + C, A, B, C = const (квадратичный закон распределения ветровых напряжений).

Будем искать решение ψ ≈ ψ уравнения (10) в виде линейной комбинации базисных функций м

^ = y.amN„,

№=1

где N_m= x^m+1y^m+1 .

Пусть граничные условия для уравнения (10) имеют вид (5) на всей границе области П . Применяя метод Галёркина с однов ре менной аппроксимацией краевых условий (при этом W_l = –W_l = N_l ) [5], получим систему линейных алгебраических

линий тока, при этом наблюдается лишь один район циркуляции жидкости – вокруг острова.

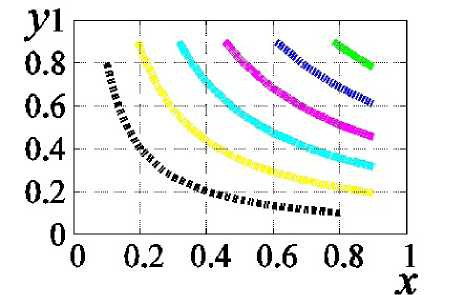
Рис. 1. Циркуляция воды в озере, M = 5, A = 2, B = 5, C = 1

уравнений относительно неизвестных коэффициентов a_m сле-

дующего вида

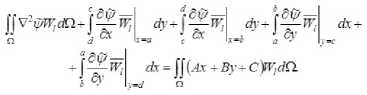
Отметим, что интегралы, входящие в (11), берутся анали-

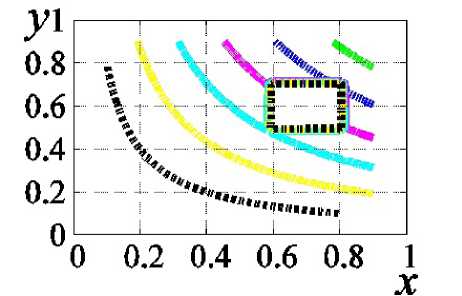
Рис. 2. Циркуляция воды в озере с островом, M = 5, A = 2, B = 5, C = 1

тически и задача сводится к решению системы линейных ал-

гебраических уравнений вида

Ka = f , где компоненты матрицы жёсткости имеют вид ( l,m = 1 ,M )

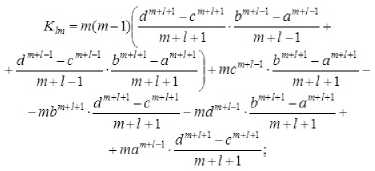
а компоненты столбца свободных членов есть

, (d^M-^ ^-^Л (d^M-c^M У⁺¹-^¹Л 1+1 / + 2 J г + 2 г+1 )

+ ' /+1 г+i

Также был рассмотрен случай, когда внутри озера находится прямоугольный остров. При этом в (11) добавляются интегралы по границе острова, а двойные интегралы берутся по области

Для численного решения задачи была составлена программа с помощью математического пакета Scilab [6]. Результаты численного решения задачи о циркуляции воды в озере приведены на рис. 1. Показаны линии тока для у = 0.5, у = 1.0, у = 3.0, (снизу вверх).

На рис. 2 представлены линии тока для случая, когда внутри озера находится прямоугольный остров. Были проведены расчёты для различных положений острова внутри озера.

В ходе численного решения задачи было установлено, что при увеличении количества базисных функций линии тока становятся более гладкими. В то же время система (11) становится хуже обусловленной, компоненты матрицы жёсткости и её определитель стремятся к нулю. В зависимости от положе-

В дальнейшем предполагается рассмотреть случай, когда озеро и/или остров являются эллипсом.

Метод частичной дискретизации

Пусть теперь прямоугольное озеро П = {( x,y ) | 0  1,0 <у <  1} подвержено воздействию ветра так, что W = Ax, A = const . Предположим, что граничные условия для уравнения (10) имеют вид ду /дх = 0 при x = 0 и x = 1; у | _у =0 = 0 и ^ I _у =1 = 1 (учтён поток от втекающей в озеро реки).

Применим метод частичной дискретизации [5]. В этом случае базисные функции зависят от одной переменной (например x ), а неизвестные коэффициенты – от другой. Будем искать решение ψ ≈ ψ уравнения (10) в виде линейной комбинации базисных функций ^=у+ ^(у)"» (Д где N m = cos ( п ■ m ∙ x ) . Отметим, что при таком выборе функций N_m граничные условия типа Неймана удовлетворяются автоматически. Подставляя ψ в (10) и выбирая весовые функции по методу Галёр-кина, получим систему обыкновенных ди фф еренциальных уравнений относительно функций a m ( у )( l = 1, M ) :

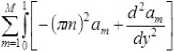
о

Вычисляя интегралы, входящие в (12), с учётом ортогональности системы базисных функций на отрезке [0;1] , имеем следующую систему обыкновенных дифференциальных уравнений ( m = 1, M ) :

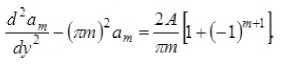
Граничные условия для системы (13) имеют вид ния острова внутри озера меняется и картина распределения

При этом граничные условия типа Дирихле удовлетворяются за счёт первого слагаемого в ψ .

Общее решение указанной системы, найденное методом

Эйлера [7], есть

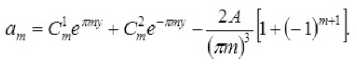
• 4.    Коннор Дж., Бреббиа К. Метод конечных элементов в механике жидкости. Л.: Судостроение, 1979. 264 с.

• 5.    Зенкевич О., Морган К. Конечные элементы и аппроксимация. М.: Мир, 1986. 318 с.

• 6.    Алексеев Е. Р., Чеснокова О. В., Рудченко Е. А. Scilab: Решение инженерных и математических задач. М.: ALT Linux; БИНОМ. Лаборатория знаний, 2008. 269 с.

• 7.    Понтрягин Л. С. Обыкновенные дифференциальные уравнения. М.: Наука, 1974. 331 с.

Произвольные постоянные интегрирования C ¹ m и Cm ² легко находятся из условий (14). Очевидно, что если m – чётное число, то C ¹ m = Cm ² = 0

Результаты решения задачи о циркуляции воды в озере с учётом потока от втекающей в него реки приведены на рис. 3,4. Показаны линии тока для ψ = 0.1, ψ = 0.3,... ψ = 0.9 , (снизу вверх).