Численная методика решения задачи деформирования полимерной кристаллизующейся среды с учетом больших деформаций

Технологический процесс производства изделий из полимерных материалов, как правило, включает этап охлаждения, сопровождающийся кристаллизацией материала. Возникающие при этом напряжения могут достигать значительных величин и приводить к снижению эксплуатационных качеств изделий вследствие больших структурных усадочных деформаций, сопутствующих переходу материала из одного фазового состояния в другое. Для адекватного представления термомеханического поведения предлагаемые модели должны быть построены в рамках теории конечных деформаций, что приводит к нелинейной постановке задач. Решение подобных задач сопряжено с большими трудностями. Кроме того, свои проблемы привносит и учет реальных условий протекания технологических процессов. Таким образом, необходимость отображения этих особенностей делает возможным получение решения задач термомеханики только с использованием численных подходов. Поэтому разработка эффективного численного алгоритма решения краевых задач термомеханики кристаллизующейся среды является актуальной.

Вопросу моделирования механического поведения полимерной среды в условиях фазовых и релаксационных переходов исследователями уделяется достаточно большое внимание. Так, в работах [1, 2] рассматривается термомеханическое поведение кристаллизующейся полимерной среды в рамках линейной теории упругости. При этом определяющие соотношения основываются

на представлении среды в виде композиции расплавленного и полностью закристаллизованного материала и описывают историю непрерывного зарождения и деформирования новой фазы в интервале температур фазовых превращений. Развивают данный подход модели, принимающие во внимание вязкоупругое поведение материала. В работах [3, 4] предложены определяющие соотношения, которые предполагают упругое поведение аморфной составляющей и линейно-вязкоупругое — кристаллической. Краевые задачи термомеханики, построенные с использованием этих соотношений, являются линейными, поэтому разработка численных алгоритмов их решения не представляет каких-либо затруднений.

Упомянутые выше модели [1–4] «работают» в условиях малости деформаций. В то же время изучаемые процессы сопровождаются значительными температурными и усадочными деформациями (до 10 % [5]), которые необходимо отражать в определяющих уравнениях новых моделей. Одним из популярных подходов, позволяющих учитывать конечные деформации, является применение операции линеаризации, заключающейся в наложении малых деформаций на конечные [6–8]. При этом процесс деформирования представляется как последовательность переходов между промежуточными конфигурациями в предположении малости деформаций на каждом переходе. В итоге решение поставленной нелинейной задачи сводится к решению последовательности линеаризованных краевых задач [9] на основе известных эффективных численных алгоритмов.

Согласно этой методике ранее (см. [10, 11]) авторами данной работы были предложены определяющие соотношения, описывающие поведение материала в процессе кристаллизации. В настоящей работе рассматривается построение численного алгоритма решения краевой задачи термомеханики кристаллизующейся упругой полимерной среды с учетом больших деформаций.

В соответствии с [10] определяющие соотношения исследуемой среды имеют вид:

^a( t )

W ( G X ) = ( 1 -a ( t ) ) W a ( G X ) + J W cr ( F ;^T ■ G X ■ F - ) d a ( x ) ,                       (1)

где W — упругий потенциал изотропного тела; Wa , Wcr — упругие потенциалы аморфной и кристаллической фаз; GX — тензор меры деформаций Коши-Грина для момента времени t; Fт — тензор-градиент места, взятый относительно момента времени те [0, t]; a(t) — степень кристаллизации материала.

В качестве упругого потенциала используется двухконстантный потенциал Пенга–Ландела [12]. C учетом его вида (1) выражение связи тензора Пиолы–Кирхгофа второго рода P ^ˆ _II с тензором меры деформаций Коши–Грина принимает вид:

P II ( t M7

- 13

■

' g - ^ G X

^{(1 -a (} t )) ⁺

a ( t )

+ J

V

Ц cr

,-13

■

f. ¹ 1 ( ^G X- 1 ) g —-—-

-

ˆ

G

X

-

T- 1

d a ( x ),

где GX-1 = FT T ■ GX ■ FT1; цa,   Ba и цcr,   Bcr — механические характеристики аморфной и закристаллизовавшейся частей материала соответственно; I1, I3 — первый и третий главные инварианты тензора меры деформаций Коши–Грина; gˆ — метрический тензор.

Алгоритм вычислений удобнее строить на основе «слабой» вариационной постановки задачи [13], которая может быть получена с помощью метода Галеркина и в случае отсутствия внешних силовых воздействий принимает вид:

J P _п --5 C dV , = 0,

V 0

где <2 = (GX - g)/2 — тензор деформаций Коши–Грина; V0 — начальный объем тела. К достоинствам рассматриваемой постановки следует отнести то, что она формулируется в исходной конфигурации. Сложность получения решения задачи в форме (3) обусловлена как нелинейностью постановки, так и проблемами, связанными с необходимостью описания возникающих температурных и структурных деформаций. Обсуждаемый в данной работе алгоритм предполагает линеаризацию постановки (3), что позволяет свести процедуру решения задачи к решению последовательности линеаризованных упругих краевых задач в рамках теории малых деформаций.

Линеаризация участвующих в постановке геометрических соотношений может быть выполнена путем разложения исходного движения тела на совокупность малых движений, вызываемых малыми приращениями внешних воздействий. Согласно идее наложения малых деформаций на конечные [8, 14], перемещения тела в произвольный момент времени представимы в виде суммы накопленных и малых перемещений, изображающих переход из промежуточной конфигурации в конечную.

Рассмотрим движение тела из начальной недеформированной конфигурации С ₀ , соответствующей моменту времени t = 0, в конфигурацию C t , которую тело приобретает в момент времени t , через промежуточную конфигурацию C_{t д t} . Положение некоторой точки в начальной конфигурации свяжем с радиус-вектором r , в конфигурациях C_{t д t} и C t — радиус-векторами R ₀ и R . Пусть U и u — векторы перемещений, описывающие переход из конфигурации С ₀ в C_{t д t} и из C_{t д t} в C_t соответственно. Каждый из этих векторов является функцией обобщенных лагранжевых координат q* ( i = 1,2,3). Предполагаем, что конфигурация C_{t д t} близка к конечной и, следовательно, перемещения u малы.

В конфигурациях C ₀ , C t _{д t} обычным образом введем локальные основные и сопряженные базисы:

Г =- ^dL,    R =^,    r = g j r    R i = (, R

* 5q* ’        0* dq* ’             « j,        0           10j, где gij и Gij — контравариантные компоненты метрического тензора в начальной и промежуточной конфигурациях. Определим операторы Гамильтона в конфигурациях C0 и Ctдt как

V = г s

а д q

0    _ v = R 0 s

d d q

Тогда тензоры-градиенты места, изображающие переход из начальной конфигурации в промежуточную, из промежуточной в конечную и из начальной в конечную могут быть записаны в виде:

/       X T /X T

0T0

1' = ( V R 0 ) T = ( V ( r + U ) ) , f = |V R |=Iv ( R 0 + u ) l ,     F = ( V R ) ^T = ( V ( R 0 + u ) ) .

Градиент места F представим через тензоры F0 и f : F = f ■ F0. Вследствие этого тензор меры деформаций т л      г       Ai х

Коши-Грина Gt тг      г         х

Коши-Грина G

,                  Ах riT ri гТ      £ ri                        1v для момента времени t примет вид: G = F1 ■ F = F0 ■ f1 ■ f ■ F0, а тензор меры деформаций

T

= f ■ f , описывающий переход из C t _{д t} в C t , с учетом малости u , станет следующим:

G = 2 e + g , где e = —I V u + IV u

T )

l l — тензор малых деформаций относительно конфигурации C_{t д t} .

Таким образом, тензор деформаций Коши–Грина, выражающий переход из начальной конфигурации Ai (х \     / ri T ri /'\/^.ri T^ri в конечную, есть C = (G - g) /2 = IF0 ■ F0 - g) /2 + F0 ■ e ■ F0 и может быть представлен как

/х       л         л *

C = С ₀ + C ,

C = 2 ( V U 0 + ( V U 0 ) ^T +V U 0 ( V U 0 ) ^T ) ,

C ^{ˆ *}

= V u +

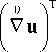
r_„ rr_„                r

+ V u ■Iv U ₀ l +Iv u l -I V U ₀ l +V U ₀ ■V u + V U ₀ -I V u l +

0T              0T

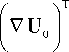
+U0 ■Vu ■[ V U0 l +V U0 ■[ V u l где U0 — вектор перемещений из начальной конфигурации в промежуточную; u — вектор малых 0

перемещений из промежуточной конфигурации в конечную; V, V — операторы Гамильтона относительно исходной и промежуточной конфигураций; Cˆ 0 и Cˆ * — тензоры, соответствующие деформациям, возникающим переходе из начальной конфигурации в промежуточную и из промежуточной в конечную.

При построении физических соотношений в случае использования нелинейных уравнений состояния существенным является вопрос учета температурных деформаций материала. Ряд авторов [15, 16] предлагает для этих целей вводить линейное слагаемое, зависящее от приращения температуры, аналогично тому, как это принято в случае использования линейных соотношений. В работе [17] используется подход, основанный на линеаризации физических соотношений в предположении малости температурных деформаций на рассматриваемом переходе. Очевидно, данная методика обладает большей общностью, хотя сразу стоит отметить существенные сложности реализации, связанные с необходимостью выделения упругой механической составляющей кинематики процесса.

В настоящей работе рассматривается построение численного алгоритма решения задач определенного класса (а именно алгоритма нахождения технологических напряжений, возникающих в процессе получения полимерных изделий), в которых деформации, будучи значительными по величине, тем не менее, не выходят за пределы порядка 10 %. Линеаризация физических соотношений проводится путем разложения тензора Пиолы–Кирхгофа P ^ˆ _II (2) в ряд Тейлора с удержанием слагаемых нулевого и первого порядков. С учетом ограниченности деформаций, характерных для изучаемого процесса, предлагается ввести температурные и структурные составляющие в форме:

a ( t )

P ii ( t ) = ( P ii ) 0 + ⁴ D a ( C o ) ■ ■ ( F oT ■ ( e - e ₀) ■ F o ) ( 1 -a ( t ) ) + J ⁴ D cr (C^ ) ■ ■ ( F T ■ ( e - e ₈) ■ F ) d a ( T ), 0

где e ₀

— тензор суммы малых температурных и структурных деформаций, сопровождающих переход из промежуточной конфигурации в конечную; тензор CoT описывает переход из конфигурации, соответствующей моменту времени т, в промежуточную; 4 Da, 4 Dcr — тензоры четвертого ранга «касательных жесткостей» аморфной и кристаллической фаз, компоненты которых зависят от Co и CoT.

В результате выполнения операции линеаризации выражение (3) преобразуется к виду:

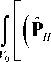
.                            / w -r

⁴ D a (C o ) ■■ ( F T ■ ( e

—

a ( t )

e _e) - IF o ) ( 1 — a ( t ) ) + J ⁴ D cr (С о т ) ■■ ( I'   ■ ( e —

e _e) . F o ) d а ( т ) -3C ’ dV o = o.

Таким образом, определение эволюции поля перемещений с течением времени сводится к решению последовательности линеаризованных задач относительно приращения вектора перемещений на рассматриваемых временных шагах.

Нахождение решения краевых задач механики для тел сложной пространственной конфигурации невозможно без использования численных методов. Среди существующих численных подходов в настоящее время наиболее широкое распространение получили те, в основе которых лежит метод конечных элементов [18]. Именно такой подход и был выбран для построения конечномерного аналога поставленной задачи. Его применение для аппроксимации выражения (4) приводит к линейным алгебраическим соотношениям, которые могут быть представлены в матричной форме [18].

Так, геометрические и физические соотношения для элемента в матричной форме выглядят следующим образом:

{ C } = { C o } + [ B ( x,U o ) ] { 8 ^e } ,

a ( t )

{ P } = { P o } + [ D a ( U o ) ] ( [ B ( x,U o ) ] { 8 e } — { A C _e} ) ( 1 — a ( t ) ) + J [ D^cr ( U o _T ) ] ( [ B ( x,U o _T ) ] { 8 ^e } — { A C , } ) d a , 0

где { б ^e } — вектор узловых неизвестных (приращений перемещений на текущем шаге); [ B ( x,U _o ) ] — матрица градиентов элемента; { A C _д} — вектор приращения температурных и структурных деформаций; [ D a ( U o ) ] , [ D cr ( U o ) ] — матрицы «касательных» жесткостей аморфной и кристаллической фаз материала. Это соотношение может быть преобразовано к виду:

{ P } = { P o } + [ D ( U o ) ][ B ( x,U o ) ] { 3 e } — [ D ( U o ) ] { A C ₉} ,

a ( t )

где [ D ( U ° ) ] = [ D a ( U ° ) ]+ J [ D c ( U ° _T ) ] da .

В целом для исследуемого тела соотношение (4) в матричной форме запишется как

E([ k ] e5 e -{fp} e -{fJ e ) = °, e где символ ^ означает суммирование по элементам; [k]e — локальная матрица жесткости элемента; e

{ f_P } e , { f ) } e — локальные векторы узловых сил, обусловленные накопленными напряжениями, температурными и структурными деформациями:

[ k ] e = J [ B ( x,U ° ) ] T [ D ( U ° ) ][ B ( x,U ° ) ] dV ,

V 0 ^e

{ f p } e = J [ B ( x,U ° ) ] ^T { P ° } dV ,

V 0 ^e

{ f > } e = - J [ B ( x,U ° ) ] T [ D ( U ° ) ] { A C ₆} dV .

^V 0 ^e

После сборки всего ансамбля конечных элементов имеем глобальную систему:

[ K (U o ) ] { u } = { F p } + { F ₈} ,

где [ K(U 0 )] — глобальная матрица системы, обладающая симметрией и зависящая от вектора накопленных перемещений U 0 ; { F p } , { F ₈} — глобальные векторы «фиктивных» усилий, обусловленные накопленными к моменту времени текущего шага напряжениями и возникающими на соответствующем переходе температурными и структурными деформациями. Таким образом, получаем последовательность линейных задач, сформулированных относительно приращений узловых перемещений. При этом оператор левой части соотношения (5) переопределяется на каждом шаге по времени, что обуславливает существенную вычислительную нагрузку при решении задач большой размерности.

Реализация предлагаемого алгоритма рассматривается на примере решения задачи охлаждения бесконечно длинной трубы, изготовленной из полимера низкого давления. Изначально материал тела нагрет до температуры, превышающей температуру плавления. Охлаждение внешней поверхности трубы производится струями холодной воды; тепловой поток на внутренней поверхности отсутствует. При охлаждении в материале протекают процессы кристаллизации, сопровождающиеся выделением тепла.

Нахождение решения осуществлялось в два этапа. На первом этапе решалась краевая задача нестационарной теплопроводности с учетом кристаллизации материала. В данной работе, в силу ограниченности возникающих деформаций, изменение конфигурации тела при решении температурной задачи игнорировалось. В результате решения температурной задачи получены данные об эволюции полей температуры и степени кристаллизации по толщине трубы с течением времени. Установленные данные использовались далее на втором этапе, на котором осуществлялось решение краевой задачи механики кристаллизующегося полимера. Временная и пространственная сетки были одними и теми же на обоих этапах. И температурная задача, и задача кристаллизации рассматривались в осесимметричной постановке.

Постановка связанной теплокинетической задачи включает:

– нестационарное уравнение теплопроводности ат а а к ат а с(T) р(Т) д- = ^1 Г X(T) d- I + p(T) Qk (a(t), r e [r-, r ]; д t r д r V       д r )

– уравнение кинетики неизотермической кристаллизации [1]

d a

— = K exp dt ¹

-

U 1 RT

-

У

Т - m

—1 ( ^{- +} A 0 « ) ( « e ( ^- ) - ^a ) , r ^e [ r 1 , r 2 ] ;

– граничные и начальные условия дTU, A дTU., А h 7 z x X z r -,

—'r = 0, —= -^T) (T (r2, t)-Ten), T (r ,0)- To, a( r ,0)- 0, r e[rp r ], где r1 , r2 — внутренний и внешний радиусы трубы; Qk — тепловой эффект реакции кристаллизации; T — температура; t — время; p — плотность материала; c — удельная теплоемкость; X — коэффициент теплопроводности; ae — равновесная степень кристаллизации; Tm — температура плавления; h — коэффициент теплоотдачи на поверхности; Ten — температура окружающей среды; T0 — начальная температура тела; R — универсальная газовая постоянная; K 1, U1, у, A — макрокинетические константы, устанавливаемые экспериментально.

Значения теплофизических и механических параметров, зависимость удельной теплоемкости, коэффициента теплопроводности и плотности полиэтилена от температуры взяты из литературных источников [5, 19–21]. Численное решение теплокинетической задачи получено разностным методом. Внутренний радиус трубы полагался равным 0,1 м, толщина стенки — 0,01 м, начальная температура тела — 470 К. При решении температурной задачи конечномерный аналог содержал 50 узлов. Временной шаг при решении задачи теплопроводности составлял 1 с. Процесс расчета прекращался при достижении во всех точках тела равновесной степени кристаллизации. Рассматриваемый временной интервал составлял 750 секунд. Решение уравнения кинетики неизотермической кристаллизации определялось численно на каждом шаге алгоритма решения краевой задачи методом Рунге–Кутты четвертого порядка, причем для обеспечения устойчивости счета временной шаг принимался равным 0,02 с. В результате решения теплокинетической задачи были получены данные о распределении температуры и степени кристаллизации для различных моментов времени.

При решении задачи термомеханики постановка предполагала реализацию плоского деформированного состояния с условием осевой симметрии. С учетом этого операторы Гамильтона записывались следующим образом:

"д Ur д r 0 0 "aur д r / 1Г1 + ^Ur 1 X    д r ) 0 0 VUo - 0 Ur r 0 0 , V u - 0 ur r3 0 o 0 0 0 0 0 где Ur , ur — радиальные компоненты векторов U0 и u соответственно. Окончательно выражения для радиальной и окружной компонент тензора деформаций Коши–Грина принимают вид:

_д u_r  1 р u_r ) Г  д u_r )д u_r       _1

r

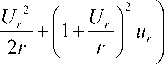
сп-,    ⁺₂   ,    + I ¹ ',, ,   c ф_Ф-^- U.

д r 2 1 д r ) I     д r ) д r           r

При построении конечно-элементного алгебраического аналога использовался двухузловой осесимметричный конечный элемент с линейной аппроксимацией узловых неизвестных, в качестве которых выступали перемещения. Все соотношения получены в базисе исходной конфигурации. Матрица градиентов элемента, вектор температурных и структурных деформаций элемента определяются по формулам

[ B ( x,U o ) ] - — ^rj ^- ri

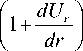
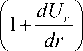
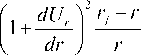
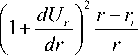
{ ^A C ₆} -^

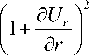
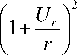
> ( P T К T + e c )

где P _T — коэффициент температурного расширения; A T , e_c — приращение температуры и структурные деформации на текущем временном шаге; r_i , r_j — радиальные координаты узлов элемента.

В соответствии с (2) компоненты матриц жесткостей имеют вид:

[ D J = 2 ц a • cr |- 3 1^ ( 2 + 4 c _фф ) - 3 | 2 1^ - 3 1 1 1-7³ ( 2 + 4 c _w) j ( 2 + 4 c _w) ^ + 4 B a , cr I^ ( 2 + 4 c _w)² , [ D " 2 cr J = [ D% J = 2 ц a ■ cr |- 3 1 3-⁴/³ ( 4 + 4 c rr + 4 c фф) - 3 |- 3 1 1 I^ ( 2 + 4 c_rr ) ( 2 + 4 c фф) + 4 1 1 I j^ J + + 4 B a • cr I -3² ( 2 + 4 c rr ) ( 2 + 4 c фф) + 2 B a ■ cr ( 1 - 1 -1² ) ,

Г d a • ^cr "l = 1 u " , ^cr I- ² 1 -^4/3f2 + 4c I-²|2/-^4/3-4/ /-^7/3f2 + 4c )h2 + 4c m + ¹ B^c • ^cr Г3²(2 + ^с V L ^D 2,2 J 2 ^ц I 3 I 3    ( ^{2 + 4} c rr ) 3 I ² I 3       3 I 1 I 3    ( ^{2 + 4} c rr ) l ( ^{2 + 4} c rr ) I ⁺ 4 B I 3    ( ^{2 + 4} c rr ) ,

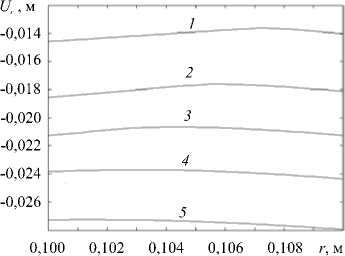
Рис. 1. Распределение радиального перемещения трубы для различных моментов времени, с: 150 (кривая 1 ); 300 ( 2 ); 450 ( 3 ); 600 ( 4 ); 750 ( 5 )

где c rr , c фф , 1 1 , 1 3 — радиальная и окружная компоненты, а также первый и третий инварианты тензора деформаций Коши–Грина C ^ˆ .

При определении напряженно-деформированного состояния конечномерный аналог расчетной области также содержал 50 узлов. Временной шаг составлял 1 секунду при длине рассматриваемого интервала в 750 секунд. На рисунке 1 представлены кривые распределения радиальных перемещений по толщине стенки трубы для различных моментов времени.

□„ЛОЛ Па

б

о,, 10"5, Па

1,5

1,0

0,5

-0.5

-1,0

-1.5

0,100   0,102   0,104   0,106   0,108 г, м

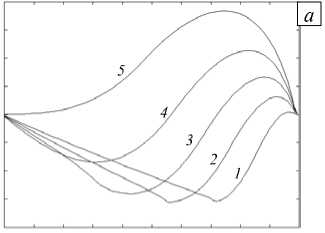
Рис. 2. Кривые распределения радиальных ( а ) и окружных ( б ) напряжений Коши по толщине стенки трубы для различных моментов времени, с: 150 (кривая 1 ); 300 ( 2 ); 450 ( 3 ); 600 ( 4 ); 750 ( 5 )

0,100   0.102   0.104   0,106   0.108 г, м

На рисунке 2 показана эволюция полей радиальных и окружных напряжений с течением времени. На начальном этапе охлаждения происходит резкая усадка внешних слоев изделия, что приводит к появлению сжимающих радиальных напряжений по всей толщине стенки трубы. В окружном направлении материал претерпевает растяжение в наружных слоях и сжатие — во внутренних. В дальнейшем происходит постепенное охлаждение и усадка материала, которой оказывают сопротивление затвердевшие внешние слои. Материал изделия в радиальном направлении постепенно переходит в зону растяжения, окружные напряжения вблизи внешней стенки становятся сжимающими. Видно, что по абсолютной величине окружные напряжения превышают радиальные на два порядка. С течением времени окружные напряжения достигают на внешнем радиусе величины, превышающей 30 МПа.

Итак, предложена методика и разработан численный алгоритм решения краевых задач термомеханики кристаллизующейся полимерной среды, которая основывается на сведении решения начальной нелинейной задачи к решению последовательности линеаризованных краевых задач. Принимаются во внимание возникающие в процессе охлаждения температурные и структурные деформации. Построены конечно-элементная аппроксимация метода и вычислительный алгоритм. Рассматривается применение предлагаемого подхода к решению задачи деформирования полимерной трубы при ее изготовлении с учетом больших деформаций и кристаллизации материала.

Работа выполнена при финансовой поддержке РФФИ (проекты № 13-01-00553-а, 13-01-96038-р_урал_а).