Численная обработка экспериментальных данных, полученных с использованием современных испытательных машин, для идентификации реологических моделей

Развитие экспериментальной техники сопровождается ростом объёмов регистрируемой информации в цифровом представлении. Современные экспериментальные установки имеют программное обеспечение, позволяющее сохранять результаты опытов в собственных форматах и экспортировать первичные текстовые файлы данных (ПТФД). Эти файлы, как правило, содержат текстовые и числовые сведения об установке, исследуемом объекте, заданных условиях воздействия и режимах регистрации, а также таблицы результатов измерения величин в различные дискретные моменты времени. Рассмотрим проблемы эффективного и наиболее полного использования таких табличных данных о результатах испытаний образцов на машине Zwick Z100SN5A в задачах идентификации и аттестации реологических моделей механики деформируемого твердого тела (МДТТ).

Программной оболочкой testXpert также создается стандартный протокол испытаний серии однотипных образцов. В рамках используемой программы испытаний по усмотрению оператора он может содержать различную графическую и числовую информацию (диаграммы деформирования, модуль Юнга, предел текучести, предельные нагрузки, предельные деформации и тому подобное), результаты простейшей статистической обработки (усредненную диаграмму деформирования, средние значения, значения

$

Оператор:	Адамов А.А.
Дата:	28.03.2006
Время:	16:04:38
Материал:	Резина НИИШП без ТО
Номер образца:	40
Ширина b0:	6.22 mm
Толщина а0:	6.18 mm
Сечение:	38.4396 mm2
Расчётная длина:	30 mm
Параллельная длина:	50 mm
Скорость:	100 mm/min
TRS - интервал времени:	0.1 s
TRS - интервал силы:	0.1 N

Замедление при переключении скорости: 1000

Данные машины:

100N5A WN:155186

Датчик перемещения траверсы WN:155186

Датчик силы ID:1	WN:155188 1000 N
Multisens	WN:155189

$

Время испыт.,с Перемещ.тр.,мм Номин.удл.,% Осевая сила,МПа

2.000092e-002, -1.558844e-004, -3.117688e-004, 2.095797e-003

8.000091e-002, -1.558844e-004, -3.117688e-004, 2.050485e-003

1.000009e-001, -1.558844e-004, -3.117688e-004, 2.095797e-003

1.200009e-001, -1.558844e-004, -3.117688e-004, 2.141109e-003

2.200009e-001, -1.558844e-004, -3.117688e-004, 2.277043e-003

3.400009e-001, -2.958437e-005, -5.916875e-005, 2.050485e-003

1.633654e+004, 6.019156e-004, 1.203831e-003, -6.966521e-003

1.633734e+004, 6.019156e-004, 1.203831e-003, -7.102456e-003

1.633762e+004, 6.019156e-004, 1.203831e-003, -7.057145e-003

Рис. 1. Типичная структура файла данных, полученного на машине Zwick Z100SN5A среднеквадратичных отклонений и коэффициентов вариации по выбранным числовым характеристикам). При проведении опытов, согласно различным стандартам на механические испытания, обычно потребность в дополнительной обработке полученных экспериментальных данных не возникает. Стандартный протокол о проведенной серии испытаний всегда можно модифицировать на основе сохраненной в собственном формате данных информации (файл с расширением *.ZSE).

В различных реологических моделях МДТТ ситуация усложняется необходимостью учета временных зависимостей регистрируемых переменных. Например, сравнительный анализ методик идентификации и аттестации моделей вязкоупругости, проделанный в [1–3], свидетельствует, что наиболее адекватными являются методики, непосредственно использующие полные измеренные истории деформации ε(t), напряжения σ(t) и/или их скоростей dε(t) dt, dσ(t)/dt . Введение допущений о мгновенном нагружении или постоянстве скоростей деформирования на активных участках нагружения и разгрузки, о постоянстве деформации на участках релаксации приводит к ухудшению адекватности идентифицируемых моделей [3].

Для иллюстрации неидеального поведения регистрируемых величин на рисунке 2 приведены фрагменты историй поведения во времени номинального напряжения σ ( t ) = P ( t )/ S ₀ ( P ( t ) — осевая сила, S ₀ —

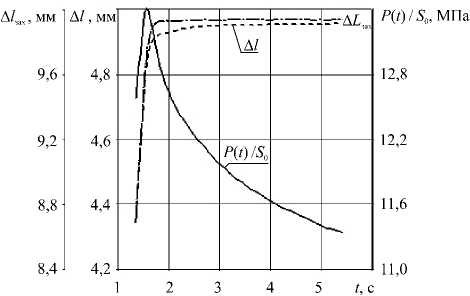
Рис. 2. Начальный участок кривой релаксации с историями перемещения траверсы и удлинения на базе однородного деформирования

площадь поперечного сечения образца в недеформированном состоянии), перемещения подвижного захвата ∆ L _зах ( t ) и удлинения базы однородного деформирования образца ∆ l ( t ) в окрестности начала релаксационного периода (в образце из резины). Инерционность подвижной траверсы и измерительных кареток датчика деформации, податливость элементов машины, нелинейное формоизменение образца вне базы однородного деформирования при уменьшающейся осевой силе — основные факторы, обеспечивающие наблюдаемое на рисунке 2 нелинейное поведение величин ∆ L _зах ( t ) и ∆ l ( t ) после выключения привода испытательной машины.

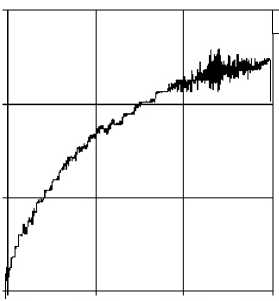
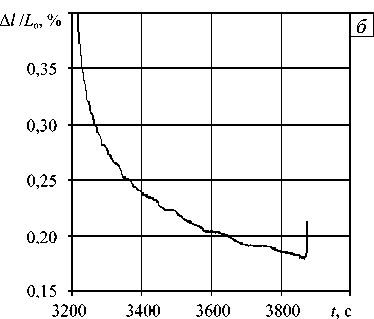
Рис. 3. История относительного удлинения образца полиэтилена на интервале релаксации при неподвижной траверсе ( а ) и на интервале его свободного сокращения после разгрузки ( б )

На рисунке 3 также показаны типичные истории деформации б ( t ) = А l ( t),L 0 ( L 0 — база измерения датчиком деформации Multisens) на интервале релаксации образца полиэтилена (5900 точек регистрации при неподвижной траверсе) и на интервале его последующего свободного сокращения после разгрузки (5800 точек регистрации при нулевой осевой нагрузке). Эти данные демонстрируют широкий частотный спектр флуктуаций измеряемой величины и особенности работы датчика Multisens, реагирующего на смещения ножевых опор при деформации образца.

Программы численной идентификации и аттестации моделей МДТТ используют процедуры дифференцирования и интегрирования историй деформирования или нагружения, поэтому прямое использование временных рядов, представленных в таблице ПТФД, неэффективно. Необходима первичная обработка этих данных, включающая в себя их фильтрацию, преобразование, сжатие и корректировку.

Комплексное решение перечисленных задач возможно с помощью кусочно-непрерывной аппроксимации опытных данных полиномами или сплайнами наилучшего приближения с учетом точек разрыва первой производной и наложением условий прохождения кривой через первую заданную точку.

Одним из подходящих для решения поставленной задачи способов является применение Fortran-процедуры SISPRG [4, 5], подбирающей сплайн наилучшего приближения на заданной совокупности точек и осуществляющей селекцию данных. Но обеспечить в процедуре условие прохождения сплайна через первую заданную точку можно лишь приближенно, с помощью весовых коэффициентов.

Аналогичная ситуация существовала при использовании В -сплайнов в рамках библиотеки IMSL 77. Тогда на концах отрезка аппроксимации можно было выполнить граничные условия лишь по производным различного порядка. В обновленной библиотеке IMSL 90 функции SPLINE_CONSTRAINTS, SPLINE_FITTING, SPLINE_VALUES устраняют этот недостаток, так как позволяют строить сглаживающий сплайн c заданным числом точек сопряжения при выполнении граничных условий, по значениям аппроксимируемой функции.

Использование полиномов Чебышева также дает возможность решить аналогичную задачу подбора аппроксимирующего полинома заданной или достаточной степени, проходящего через первую выбранную точку. Проблема заключается в определении у полинома наилучшей степени согласно выбранному критерию оптимальности [4–5].

Далее приведены результаты решения поставленной выше задачи с помощью сплайнов наилучшего приближения (СНП) и полиномов наилучшего приближения Чебышева (ПНПЧ).

2.    Общее описание процедуры обработки

Для зарегистрированной переменной y(t) имеем дискретный временной ряд c произвольным шагом по времени l(tk,yk), к = 1,N I, где N — число точек измерения. Среди этих точек на основе графического анализа данного ряда в порядке возрастания времени устанавливаем точки разрыва первой производной (ТРПП) (t(i), i = 0, Np, Np < N, где Np — число ТРПП). Первая ТРПП должна соответствовать началу опыта (t(0) > t1). Одновременно с определением первого разрыва принимается решение о значении y01) = y (t<0)) и преобразовании сдвига для всех yk (к = 1, N) — сдвиг принимается равным разности измеренного y

(t™)

и назначенного

y ( t ⁽⁰⁾ ) значений.

Необходимость проведения сдвига диктуется тем, что в программе испытаний обычно задается малая предварительная нагрузка на образец для компенсации всех зазоров в соединениях испытательной машины и/или выпрямления образца по типу натяжения нити. При обработке данных тензометрии аналогичная проблема обусловливается неточной исходной балансировкой тензомостов. Если y ( t (0) ) и значения y ( t (0) ) не совпадают и принято решение о выполнении преобразования сдвига, то оно выполняется до построения всех аппроксимирующих зависимостей.

Практика использования сдвига по оси ординат для данных тензометрии выявила логическую ошибку в сдвиге по измеренному значению y ( t (0)) — прежде чем его делать, необходимо предварительно сгладить переменную на первом отрезке между ТРПП для вычисления сглаженного значения y ( t (0) ) , которое и следует использовать вместо y ( t (0) ) .

Пример таких первичных данных тензометрии, зашумленных высокочастотными помехами со значительной амплитудой, показан на рисунке 4, а (частота опроса 1 кГц; приведено одно значение из пятидесяти измеренных при испытании на растяжение образца из углепластика с наклеенными тензорезисторами). Измеренное значение y (t(0)) поперечной деформации s2 в окрестности начала опыта t(0) ® 4,85 с имеет размах регистрируемой величины.

Предварительная процедура Fortran-подпрограммой DCSSMH

помехи — это приблизительно десятки процентов от диапазона сглаживания для вычисления y (t(0)) выполняется библиотечной

[6] с заданием естественных граничных условий. Если существует

необходимость преобразования сдвига по оси ординат всех измеренных значений y ( t ( k ⁾ ) , то сдвиг, независимо от уровня помех, выполняется на величину y ( t (0) ) - y ( t (0) ) . Назначение t (0) остается в этом случае творческой задачей, решаемой исследователем на основе различных практических обстоятельств.

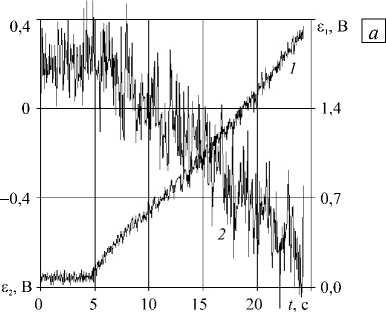
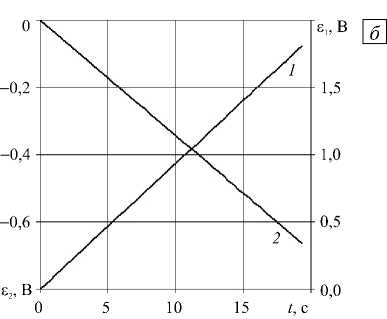
Рис. 4. Исходные ( а ) и аппроксимированные сплайном наилучшего приближения ( б ) истории продольной £ (кривая 1 ,

коэффициент усиления к усил = 200 ) и поперечной £ ₂ (кривая 2 , к у_СИл = 2000 ) деформации

Затем при визуальном графическом анализе для каждого j -го интервала времени ( j = 1, N p ) при числе точек наблюдения N_j в зависимости от характера поведения y ( t ) на полуотрезке между соседними ТРПП [ t ⁽ j ^{- 1)} , t ⁽ j ⁾ ) выбирается обычная или логарифмическая нормированная локальная шкала времени L , имеющая значение 0 в левой точке. Значения глобального времени наблюдения t_k преобразуются в локальные значения L i ( i = 1, N j ; L 1 = 0). Использование логарифмической шкалы времени для участков кривых, соответствующих режимам релаксации и ползучести, позволяет существенно уменьшить число точек сопряжения сплайна (или порядок полинома Чебышева) для достижения удовлетворительной точности аппроксимации на этих участках.

Также для каждого временного интервала априори визуально оценивается и задается максимальное nmj ax   (задание редких случаях,

число точек сопряжения кубических сплайнов (максимальный порядок ПНПЧ) максимального числа точек гарантирует прекращение итерационного процесса в тех когда отсутствует минимум величины, выбранной в качестве критерия на j -м отрезке).

Далее на каждом j -м ( j = 1, N p ) от количества точек измерения N_j , интерполяционных полиномов степени первую заданную точку у ( t ⁽ j ^{- 1)} ) = у 0 j ⁾ .

интервале времени между соседними ТРПП, в зависимости строится аппроксимация при N j = 2 ^ 4 в виде обычных от 1 до 3, при N j >  4 — СНП или ПНПЧ, проходящих через

При итерационном подборе оптимального числа точек сопряжения сплайна n_j (c равномерным распределением узлов сопряжения на отрезке аппроксимации — «кардинального» сплайна [6]) это число варьируется от - 2 (линейная аппроксимация — линейная регрессия) до заданного n max . Для ПНПЧ при подборе оптимального порядка полинома порядок варьируется от 1 до заданного максимального значения n ^m _j ^ax .

Найденное число точек сопряжения сплайна (или порядок полинома Чебышева) определяется четырьмя последовательно срабатывающими факторами: числом точек измерения, достигнутым уровнем дисперсии остатков, выбранным критерием оптимальности сплайна (полинома Чебышева), заданным максимальным числом nmj ax точек сопряжения (порядком полинома Чебышева). Наилучшее приближение получается при выходе из итерационного процесса подбора только по критерию оптимальности, в остальных случаях строится аппроксимация согласно задаваемым ограничениям.

Для j > 1 в качестве первой заданной точки у0j) = у(j 1) (t(j 1)) принимается значение, вычисленное по аппроксимации предыдущего отрезка. Таким способом достигается непрерывность аппроксимирующей функции в ТРПП. Использование СНП является более приемлемым по сравнению с ПНПЧ по ряду известных обстоятельств, практически важных при первичной обработке экспериментальных данных: полиномы не так универсальны при аппроксимации произвольных функций; с ростом порядка полинома ухудшается обусловленность матрицы системы линейных алгебраических уравнений для нахождения его коэффициентов.

Во внутренних узлах сплайнов (при числе точек сопряжения n j >  1) для каждого j -го отрезка аппроксимации выполняются условия непрерывности самой функции и её первой производной. По второй производной для граничных и внутренних узлов сплайнов 3-й степени реализуется выбор из трех комбинаций условий:

• 1.    у"(t) разрывна во внутренних узлах и произвольна в граничных узлах (сплайн с дефектом 2);

• 2.    у"(t) непрерывна во внутренних узлах и произвольна в граничных узлах (сплайн с дефектом 1);

• 3.    у"(t) непрерывна во внутренних узлах и задана в граничных узлах у"(t⁽j^-1)) = у"(t⁽j)) = 0 (естественный сплайн с дефектом 1).

3.    Построение сплайна наилучшего приближения, проходящего через первую заданную точку

Здесь дефект сплайна — это разность между степенью сплайна и наивысшим порядком непрерывной на отрезке производной. Последний тип граничных условий позволяет получить СНП максимальной гладкости.

Представленные числовыми рядами [ ( t k , у_к ), к = 1, N ] данные в значениях зависимой регистрируемой величины y_k содержат, наряду с интересующей нас регулярной (детерминированной) составляющей, случайные компоненты, обусловленные как статистически неоднородным строением исследуемых образцов материалов, так и внешними факторами, связанными с процессами измерений и преобразования данных. Такие случайные составляющие присущи, в меньшей мере, и независимой переменной t_k , но обычно её считают детерминированной величиной, перенося всё случайное в зависимую переменную y_k .

Аппроксимация опытных данных априори предполагает существование детерминированной связи y ( t ) между регулярными составляющими этих переменных на статистически значимом уровне, достаточном для её восстановления на фоне случайных составляющих. Задача восстановления такой регрессионной зависимости относится к числу неопределенных и неоднозначных; результат её реализации обуславливается многими субъективными факторами. Поэтому оптимальная аппроксимация для предполагаемого множества разнообразных данных при отсутствии знаний о законах распределения случайных составляющих и их частотном спектре осуществима лишь при использовании алгоритмов на основе многоэтапных итерационных процессов с возможностью коррекции принятых допущений на каждом этапе.

Для построения приближения в рассматриваемой проблеме обработки экспериментальных данных с помощью сглаживающих сплайнов известного порядка часто используется минимизация выражения [7]

^S N,

+ (1 - p ) J [ S p ( j S ) ] 2 d S

S 1

.    ^ [ у , (У - S p ( j S , )] ²

5 ¹ , -’⁽ a j , p ) = p X------------------

^ min,

i=1              Wi или близкого к нему выражения [11]

^S Nj

+ a j [ S p ( a , ; S ) ] ² d s > min,

S 1

. А [ y , ( S i ) - S а ( j S , )] ²

• ⁵ j ⁾⁽ а , , ^{а ) -} X---------------

• ,=1           w

где S ( a j ; S i ) — значение аппроксимирующего сплайна в точке S i , определяемого вектором коэффициентов сплайна (полинома) a j ; w i — весовые коэффициенты («оценки») заданных значений, отражающие в идеальном случае доверительный интервал измеренных данных; p е [0,1] — выбранный некоторым образом параметр сглаживания, регулирующий степень приближения к заданным значениям и получение гладкой функции; а > 0 — параметр сглаживания. Параметры сглаживания p и а либо назначаются априори, либо итерационно уточняются каким-то методом, пригодным для построения наилучшего приближения.

Традиционное использование базиса В -сплайнов для построения искомого сплайна нерационально при предполагаемом большом количестве точек, по которым вычисляется аппроксимирующая функция в процедурах идентификации материальных функций. К существенно меньшей трудоемкости вычислений приводит кусочно-многочленная форм а пред ставления сплайна

• ⁽⁰⁾ z>⁽¹V? ?' ¹ z>⁽²⁾        ?^{( 1} )\² л⁽³) ?^{( 1 )}'l^{3                  ( 1 -1)} 4^{( 1 )_}|                                        Р^{( 1} )

S ^{( a}j ^{; S )} - ^aj, + ^aj, ^{( S} - ^S j ) ^{+ a}j[ ^{( S} - ^S j ) ^{+ a} ,1 ^{( S} - ^S j ) , V ^Se [ ^S j , ^S j ] ^{( 1} - 1, n j + ¹ ), ^{где S} j  внешние и внутренние узлы сплайна для j -го отрезка аппроксимации.

В данной работе математическая постановка задачи аппроксимации сплайном на любом j -м отрезке между соседними ТРПП основана на условной минимизации функции Лагранжа

,               Nj [ у^й , ¹ - S ⁽ a ^; S i ) ] ^{2 j}            ■

L 5(aj, Xj) X--------2--X jk (aj) ^ min, i-1             W                k-1

обеспечивающей удовлетворение системы линейных ограничений c_k ( a j ) - 0 ( k - 1, m j ), то есть всех граничных условий и условий стыковки во внутренних узлах сопряжения сплайна методом X -множителей Лагранжа. Например, для естественного сплайна с одной точкой сопряжения ( n j - 1) на отрезке с узлами S j ⁰⁾ - 0, s ' , ¹', S j²⁾ система линейных ограничений включает шесть уравнений ( m j - 6), имеющих вид:

a '1 - У1 - 0, a (1 - 0,

л(0) -I- />(1)?(1)   /,(2) (?(1) V />(3) (р(1) V   „(°) - л aj1 + aj1 Sj + aj1 (Sj ) + aj1 (Sj ) - aj2 - 0,

d l д a j 0 = , = 0 [дХ jk

дL   п    дL   _    дL   _  л  :----- г- д a"    0    д a (-2)    0    д a >    0    ( l  1, n j+ 1); jl                   jl                   jl                                                                        (2) ( k = 1, m j ).

Систему (2) можно упростить благодаря возможности непосредственного определения двух коэффициентов сплайна из ограничений (1 1 ) и (1 2 ): a (1 = y ^) = y f ^{j )} (для a if) = y ₁( ^ ₁) = У о* ¹ ) и a (I = 0). Исключение этих коэффициентов из системы линейных алгебраических уравнений (2) и соответствующих ограничений из (1) позволяет снизить порядок решаемой системы.

Для устранения численных проблем, связанных с кусочно-многочленной формой представления сплайна, в Fortran-программе использована двойная точность при формировании и решении системы линейных алгебраических уравнений, а также решение этой системы методом Гаусса с выбором главного элемента.

В рассматриваемой задаче важен подбор наилучшего приближения, позволяющего представлять в функции аппроксимации наилучшим образом только регулярную составляющую данных. Очевидно, что повышение степени близости к исходным данным при наличии в них случайных составляющих с какого-то определенного порядка модели будет не приближать функцию аппроксимации к регулярным составляющим данных, а наоборот — увеличивать расхождение. Предельным случаем служит вырождение сглаживающего сплайна в интерполяционный, когда обеспечивается прохождение сплайна через все измеренные точки.

Так как информация о дисперсии и спектральном составе случайных составляющих регистрируемой величины остается неизвестной, оптимальный порядок аппроксимации в данной работе определяется методом последовательных приближений с постепенным наращиванием порядка статистической модели и сравнением количественного различия дисперсии остатков (разностей измеренных и аппроксимированных значений) на каждом новом приближении с её значением на предыдущем приближении по одному из трех критериев оптимальности (для удобства сравнения аппроксимаций на разных участках кривой используется дисперсия остатков, приходящаяся на одну аппроксимируемую точку). Использованы критерии сравнения:

– относительная дисперсия, приходящаяся на одну аппроксимируемую точку;

• - относительная дисперсия остатков, приходящаяся на одну степень свободы аппроксимации ( n j - m j + 1);

  – величина функционала эмпирического риска [4, 5] (с принятым априори значением доверительной вероятности 0,99).

При повышении степени приближения (начиная с уравнения линейной регрессии) значимость различия относительных дисперсий сначала довольно высока, затем она постепенно уменьшается, а в области оптимальных порядков становится малозначимой. После прохождения оптимальной зоны значения дисперсий остатков снова начинают расти с увеличением значимости различий.

Обрабатываемые временные ряды могут содержать редкие выбросы и грубые ошибки, которые вызываются разными причинами. Их влияние устраняется итерационной процедурой селекции (цензуры) [4] данных по следующей схеме:

• 1.    При предварительном графическом анализе данных визуально выявляется необходимость такой цензуры и задается максимально допустимое число n_j ^уд удаляемых точек на j -м отрезке.

• 2.    Выполняется одно из последовательных приближений функции аппроксимации на j -м отрезке.

• 3.    Вычисляется дисперсия остатков и определяется точка с максимальным остатком.

• 4.    Если остаток в этой точке лежит внутри интервала, определяемого с принятой априори доверительной вероятностью 0,9999 по всем остаткам рассматриваемого отрезка с использованием гипотезы о нормальном распределении остатков и/или п уд = 0, процедура селекции данных для рассматриваемого приближения функции аппроксимации на j -м отрезке заканчивается.

• 5.    Иначе эта точка удаляется из рассмотрения, строится новое приближение с тем же порядком аппроксимации и оценивается эффект исключения точки по выбранному критерию оптимальности аппроксимации.

• 6.    Если критерий оптимальности не улучшается, точка возвращается в рассматриваемую совокупность; в противном случае принимается n j = n j - 1 и совершается возврат в пункт 3.

  

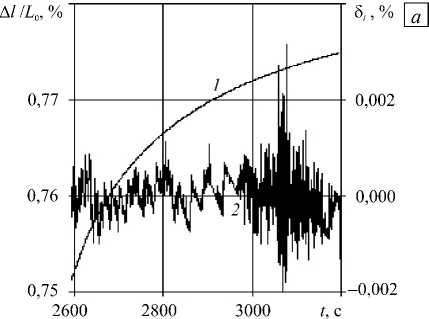
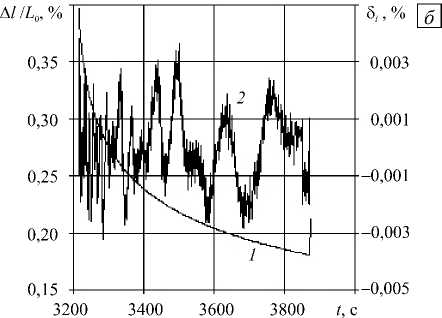
  Рис. 5. Аппроксимации историй относительного удлинения (линии 1 ) и соответствующие остатки (линии 2) на интервале релаксации образца полиэтилена при неподвижной траверсе ( а ) и на интервале его свободного сокращения после разгрузки ( б )

  
  
  
  
  
4. Заключение

На рисунке 5 приведены результаты аппроксимации СНП для двух отрезков историй относительного удлинения y_i ( ξ _i ) =∆ l ( ξ _i ) L ₀ и остатки (невязки) δ _l ( ξ _i ) ≡ y_i ( ξ _i ) - S _α ( a _j ; ξ _i ), соответствующие экспериментальным данным с рисунка 3.

Для контроля в процессе подбора аппроксимации в N_j точках измерения фиксируется информация о достигнутом оптимальном числе точек сопряжения сплайна n_j при заданном n ^m _j ^ax , максимальном отклонении по модулю δ _i в точке i и номере этой точки. Также регистрируется дисперсия D_{j 1} , приходящаяся на одну точку. В таблице приведены эти данные для двух отрезков историй удлинения, показанных на рисунках 3 и 5. Они свидетельствуют о существенном повышении точности аппроксимации при увеличении числа сопряжений сплайна при сравнительно малом их числе.

Таблица. Информация о поиске оптимального числа сопряжений на j -м отрезке

Число точек измерения N j	n m j ax	n j	δ i	i	D j 1
5898	0	0	0,068	1	0,14 10 -07
	2	2	0,0062	60	0,38 10 -09
	5	4	0,0032	4822	0,42 10 -10
5764	0	0	0,096	45	0,15 10 -06
	2	2	0,020	14	0,12 10 -08
	5	4	0,0037	2518	0,28 10 -09

Примером эффективности описанной процедуры первичной обработки экспериментальных данных могут служить истории осевой деформации и нагрузки при испытании образца сильвинита в условиях объёмного напряженного состояния с участками релаксации, разгрузки и отдыха, измеренные в 87531 точке по времени. Для этих историй определены, соответственно, 16 и 19 точек разрыва 1-й производной; в результате аппроксимации эти истории заданы сплайнами с 34 и 54 узлами соответственно. Сжатая таким образом экспериментальная информация по историям обработанных переменных каждого опыта хранится в двух одномерных целочисленных файлах-указателях и реальном одномерном массиве коэффициентов.

Для вычисления значения нужной переменной и/или её 1-й производной достаточно в соответствующей вычислительной процедуре задать номер переменной и значение аргумента. При использовании совокупности опытов для идентификации какой-либо материальной функции [2, 3] одномерные массивы с хранимой экспериментальной информацией без труда объединяются в двумерные массивы.

Представленная методика сглаживания, сжатия и преобразования экспериментальных данных в виде историй измеряемых параметров сплайнами наилучшего приближения с учетом точек разрыва первой производной прошла вместе с автором длительный эволюционный путь от кусочно-непрерывной аппроксимации экспериментальных графиков с бумажных диаграмм полиномами 2-го порядка до описанного здесь состояния. На её основе легко реализуются численные методики идентификации и верификации реологических моделей МДТТ, содержащих истории измеряемых параметров и/или их скоростей.

Методика оказалась эффективной и для обработки данных, получаемых с использованием современных цифровых систем сбора данных различной природы.

Автор благодарен С.С. Двойникову за выполнение аналогичной реализации с использованием полиномов Чебышева и сравнительный анализ полученных аппроксимаций.