Численная реализация метода поверхностного движения для решения задач линейного программирования

Эпоха больших данных и индустрия 4.0 породили задачи линейного программирования (ЛП) сверхбольших размерностей, включающих в себя миллионы переменных и миллионы ограничений [1 –4] . Во многих случаях объектом линейного программирования являются задачи, связанные с оптимизацией нестационарных процессов [5] . В нестационарных задачах ЛП целевая функция и/или ограничения изменяются в течение вычислительного процесса. Также среди этого класса задач встречаются приложения, в которых необходимо выполнять оптимизацию в режиме реального времени. Для решения таких задач необходимы масштабируемые методы и параллельные алгоритмы линейного программирования.

Один из стандартных подходов к решению нестационарных задач оптимизации состоит в том, чтобы рассматривать каждое изменение как появление новой задачи оптимизации, которую необходимо решать с нуля [5]. Однако такой подход часто непрактичен, поскольку решение проблемы с нуля без повторного использования информации из прошлого может занять слишком много времени. Таким образом, желательно иметь алгоритм оптимизации, способный непрерывно адаптировать решение к изменяющейся среде, повторно используя информацию, полученную в прошлом. Этот подход применим для процессов реального времени, если алгоритм достаточно быстро отслеживает траекторию движения оптимальной точки. В случае больших задач ЛП последнее требует разработки масштабируемых методов и параллельных алгоритмов ЛП.

До настоящего времени наиболее популярными методами решения задач ЛП являются симплекс-метод [6] и методы внутренних точек [7] . Эти методы способны решать задачи с десятками тысяч переменных и ограничений. Однако масштабируемость параллельных алгоритмов, основанных на симплекс-методе, в общем случае ограничивается 16–32 процессорными узлами [8] . Что касается алгоритмов внутренних точек, они не поддаются эффективному распараллеливанию в общем случае. Это ограничивает применение указанных методов для решения сверхбольших нестационарных задач ЛП в режиме реального времени. В соответствии с этим задача разработки масштабируемых методов и эффективных параллельных алгоритмов ЛП для кластерных вычислительных систем остается актуальной.

В недавней работе [9] было дано теоретическое описание нового метода ЛП — метода поверхностного движения, строящего на поверхности допустимого многогранник а1 оптимальный целевой путь к решению задачи ЛП. Под оптимальным целевым путем понимается путь по поверхности допустимого многогранника в направлении наибольшего увеличения значений целевой функции. Однако предложенный в этой статье алгоритм 1 на шаге 15 требует нахождения на границе гипердиска точки с максимальным значением целевой функции. При этом не приводится численный алгоритм, позволяющий выполнить этот шаг. В этой статье мы приводим и исследуем алгоритм AlFaMove, устраняющий допущенный пробел.

Статья организована следующим образом. Раздел 1 содержит теоретический базис, необходимый для описания метода поверхностного движения и его численной реализации. Раздел 2 посвящен описанию операции псевдопроекции, позволяющий найти вектор движения по оптимальному целевому пути для линейного многообразия, получаемого в результате пересечением гиперплоскостей. В разделе 3 дается формализованное описание алгоритма AlFaMove, представляющего собой численную реализацию метода поверхностного движения. Раздел 4 посвящен описанию параллельной версии алгоритма AlFaMove. В разделе 5 представлены информация о программной реализации алгоритма AlFaMove и результаты экспериментов на кластерной вычислительной системе по исследованию его масштабируемости. В заключении суммируются полученные результаты и намечаются направления дальнейших исследований.

1. Теоретический базис

Данный раздел содержит необходимый теоретический базис, используемый для описания алгоритма движения по граням AlFaMove. Рассмотрим задачу ЛП в следующем виде:

ж = arg max {( с , ж ) | А ж <  b } ,                             (1)

\bfitx\in\BbbRn где с G Rn, b Е Rm, A Е Rmxn, m > 1, с = 0. Здесь (•, •) обозначает скалярное произведение двух векторов. Мы предполагаем, что ограничение \bfitx \geqslant \bfzero также включено в матричное неравенство A\bfitx \leqslant \bfitb в форме

- \bfitx \leqslant \bfzero .

Линейная целевая функция задачи (1) имеет вид f (ж) = (с, ж).

Вектор с в данном случае является градиентом целевой функции f ( ж ).

Пусть \bfita i \in \BbbR ⁿ обозначает вектор, представляющий i -тую строку матрицы A . Мы предполагаем, что a i = 0 для всех i G { 1,...,m } . Обозначим через H i замкнутое полупространство, определяемое неравенством langle \bfita i , \bfitx rangle \leqslant b i , а через H i — ограничивающую его гиперплоскость:

Hi = {ж G Rn|(ai, ж) < bi};(2)

Hi = {ж G Rn| (ai, ж) = bi}.(3)

Определим допустимый многогранник

m

M = П Hi,(4)

i =1

представляющий множество допустимых точек задачи ЛП (1) . Заметим, что M в этом случае будет замкнутым выпуклым множеством. Мы будем предполагать, что множество M является ограниченным и M = 0 , то есть задача ЛП (1) имеет решение.

Дадим определение рецессивного полупространства [10] .

Определение 1. Полупространство Hi называется рецессивным, если жх G Hi, VX> 0 : ж + Хс G Hi.                            (5)

Геометрический смысл этого определения состоит в том, что луч, исходящий в направлении вектора \bfitc из любой точки гиперплоскости, ограничивающей рецессивное полупространство, не имеет общих точек с этим полупространством, за исключением начальной. Известно [10] , что следующее условие является необходимым и достаточным для того, чтобы полупространство H i было рецессивным:

( a i , с ) >  0.

Определим

I = {i G { 1,... ,m } |( a i , с ) > 0 } ,                                   (6)

то есть I представляет множество индексов, для которых полупространство H i является рецессивным. Поскольку допустимый многогранник M представляет собой ограниченное множество, имеем

I = 0 .

Положим м = П Hii.                                 (7)

i \in\scrI

Очевидно, что MI является выпуклым, замкнутым, неограниченным многогранником. Будем называть его рецессивным. Из (4) и (6) следует

M С M.

Обозначим через Г(М) множество граничных точек допустимого многогранника M, а через Г(М) — множество граничных точек рецессивного многогранника M2. Согласно утверждению 3 в [10] имеем х G Г(М), то есть решение задачи ЛП (1) лежит на границе рецессивного многогранника M.

Следуя [11] , дадим определение ортогональной проекции на гиперплоскость.

Определение 2. Пусть в пространстве \BbbR ⁿ имеется гиперплоскость

H = { х G R n |( а , х ) = Ь } .

Ортогональная проекция ^ н ( г ) точки v G R n на гиперплоскость H определяется формулой

„„( v ) = v - < ^ 1^^ а .                         (8)

^H                                      \| \bfita \| ²

Следующее утверждение дает способ вычисления оптимального пути на гиперплоскости.

Утверждение 1. Пусть в пространстве \BbbR ⁿ задана гиперплоскость H с нормалью \bfita \in \BbbR ⁿ , проходящая через точку \bfitu \in \BbbR ⁿ :

H = {х G Rn |(а, х) = (а, и) } .(9)

Пусть задана линейная функция f ( х ) : R n ^ R с градиентом с G R n :

f (х) = (с, х).(10)

Пусть векторы \bfita и \bfitc линейно независимы (не коллинеарны, и среди них нет нулевого вектора). Положим v = и + с.(11)

Построим ортогональную проекцию ^ н ( v ) точки v на гиперплоскость H :

w = ^н (v).(12)

Тогда вектор d = w — и однозначно задает направление максимального увеличения линейной функции f ( х ), определяемой формулой (10) .

Доказательство. Предположим противное, то есть существует точка w G H такая, что

(с, W) > (с, w),(13)

||w — и || = ||w — и || и w = w (см. рис. 1) . Здесь и далее || • || обозначает евклидову норму. Вычислим ( с , w ). В соответствии с определением 2 ортогональная проекция ^ н ( v ) точки

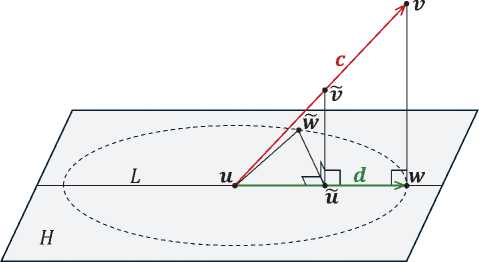
Рис. 1. Иллюстрация к доказательству предложения 1.

Пунктиром обозначена гиперокружность с радиусом \| \bfitw - \bfitu \|

v на гиперплоскость H , задаваемую формулой (9) , вычисляется следующим образом:

w = v —

( a , v — и ) \| \bfita \| ²

а .

Подставив вместо \bfitv правую часть формулы (11) , получим

( а, с] w = и + с-- а^а-                            (14)

\| \bfita \| ²

Используя (14) , находим

^{( с} , ^{w ]} = ^{( с} , и ) + ||^с|| 2 - ^{( а},^ 2- .                                 ⁽¹⁵⁾

\| \bfita \| ²

Поскольку \bfita и \bfitc линейно независимы, в соответствии с неравенством Коши–Буняковского имеем

( а , с ) 2 <  | а | ² -Ц с Ц ² .

Отсюда следует

\| \bfitc \| ²

^{( а} , ^{с )} 2 \| \bfita \| ²

> 0.

Теперь вычислим ( с , гт ) . Определим и = ^ l ( W) — ортогональная проекция точки w на прямую L, проходящую через точки и и w . По построению существует число 5 G К , удовлетворяющее условию

— 1 <  5< 1, (17)

такое, что и = и + 5(w — и).

Положим

V = и + 5( v — и ).                                (18)

Тогда точка и является ортогональной проекцией точки V на гиперплоскость H , определяемую формулой (9) , и может быть вычислена следующим образом:

( а , V — и )

и = v--—а .

\bfita \| ²

Подставив вместо v правую часть формулы (18), отсюда получим и = и + 5 ^v — и —

\langle \bfita , \bfitv - \bfitu

\| \bfita \| ²

^\rangle \bfita .

Используя (11) , произведем замену v — и = с :

\langle \bfita , \bfitc \rangle

и = и + О с-- ad \ •

\| \bfita \| ²

Очевидно, w = (w — и) + й.

Заменим второе слагаемое в (20) на правую часть формулы (19) :

\langle\bfita, \bfitc\rangle w = (w — и) + и + О с--ad \ •

\| \bfita \| ²

Отсюда получаем

[ с , Ид ) = [ с , w — й) + [ с , и ) + 5 ^|с | 2 —

\langle \bfita , \bfitc \rangle ² \| \bfita \| ²

)

По построению вектор w — U ортогонален вектору v — и = с . образом, последняя формула преобразуется к виду

Поэтому [ с , w — и ) =0. Таким

^[с, ы) = (с, и) + 5 ^||^с||2 ^—

\langle \bfita , \bfitc \rangle ² \| \bfita \| ²

)

Сопоставляя (15) и (21) , с учетом (16) и (17) получаем

[с, w) < [с, w) , что противоречит (13).

^

Возвращаясь к задаче ЛП (1) , можно сказать следующее. Пусть и G M И Г(М) существует единственная рецессивная гиперплоскость H i \prime (i ^\prime \in \scrI ) такая, что \bfitu \in H i \prime .

и

В

этом случае вектор \bfitd, определяющий направление оптимального целевого пути из точки \bfitu, в соответствии с утверждением 1 вычисляется по формуле d = с —

( a i/ , и + с ) — b i >

\| \bfita i \prime \| ²

\bfita i \prime .

В следующем разделе мы рассмотрим общий случай, когда через точку \bfitu проходит несколько гиперплоскостей.

2.    Операция псевдопроектирования на линейное многообразие

Пусть J С {1,...,m}, ^" = 0, и Р| Hi = 0. В этом случае множество индексов J i\in\scrJ определяет в пространстве \BbbRn линейное многообразие

L = П H i .

i\in\scrJ

Обозначим kL — размерность линейного многообразия L. При k L < n — 1 многообразие L не является гиперплоскостью, и для определения вектора движения \bfitd по этому многообразию в направлении максимального увеличения целевой функции нельзя применить формулу (22) , так как такое линейное многообразие невозможно задать одним линейным уравнением в пространстве \BbbR ⁿ . Однако мы можем найти указанный вектор \bfitd с помощью операции псевдопроектирования [10] . Определим проекционное отображение ^ ( - ):

^^{( х )} = ш ^ ^ Н' ^(х) '

Известно [12], что отображение ^(х) является непрерывным L-фейеровским отображением, и последовательность точек

|X k = ^^к ( ж о)| k =1

порождаемая этим отображением, начиная с произвольной точки \bfitx 0 \in \BbbR ⁿ , сходится к точке, принадлежащей L :

Xk —у x G L.

Теперь мы готовы дать определение псевдопроекции на линейное многообразие, образуемое пересечением гиперплоскостей.

Определение 3. Пусть \scrJ \subseteq { 1,...,m } , J = 0 , Hiey H i = 0 , ^ ( ' ) — проекционное отображение, определяемое формулой (24) . Псевдопроекцией p j ( х ) точки X G R n на линейное многообразие L = i\^H H i называется предельная точка последовательности (25) :

k4« | p j ^{( X )} - ^ k ^{( X )} I I =°’

Важным свойством псевдопроекции на линейное многообразие является то, что в этом случае псевдопроекция совпадает с ортогональной проекцией. Для доказательства этого факта нам понадобится следующая лемма.

Лемма 1. Пусть в пространстве \BbbR ⁿ заданы гиперплоскость H i \prime и линейное многообразие L , принадлежащее этой гиперплоскости:

H i - = { х G R n | { a ^ , х ) = hr } ;

^L =А« H i ;

i ^\prime in scrJ .

Обозначим через P линейное многообразие, являющееся ортогональным дополнением к L :

P = L^.

Тогда для любой точки \bfitv , принадлежащей линейному многообразию P , ее ортогональная проекция ^ H i , ( v ) на гиперплоскость H i ' также будет принадлежать линейному многообразию P :

V v G P : л Не ( v ) G P.

Доказательство. Обозначим \bfitp — ортогональная проекция точки \bfitv на гиперплоскость H i \prime :

p = л H i ' ( v ).

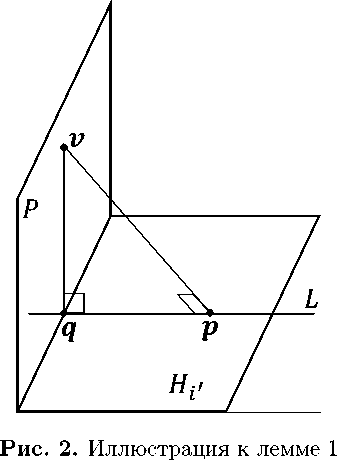
Без ограничения общности мы можем считать, что \bfitp \in L (см. рис 2) . Предположим, что точка \bfitp не принадлежит линейному многообразию P . Обозначим \bfitq — точка пересечения линейного многообразия L с его ортогональным дополнением P :

q = L П P.

Поскольку P является ортогональным дополнением к линейному многообразию L , точка \bfitq является ортогональной проекцией точки \bfitp на линейное многообразие P :

q = ^ p ( p ).                                       (28)

Рассмотрим треугольник A ( r , p , q ). В силу (27) угол Z p с вершиной в точке p является прямым. В в соответствии с (28) угол \angle \bfitq с вершиной в точке \bfitq также является прямым. Но это возможно только в случае, когда p = q , то есть

\bfitp \in P.

Лемма доказана.

Следующее утверждение доказывает, что псевдопроекция на линейное многообразие совпадает с ортогональной проекцией.

Утверждение 2. Пусть выполняются следующие условия:

JQ {!,...,т},                                    (29)

L = Q H i ,L = 0 ;                           (30)

i\in\scrJ где Hi = {ж g Rn| {ai, ж) = bi}. Обозначим ^l(x) — ортогональная проекция точки ж € Жп на линейное многообразие L. Тогда

Pl(x) = ^l(x), то есть, псевдопроекция на линейное многообразие L совпадает с ортогональной проекцией.

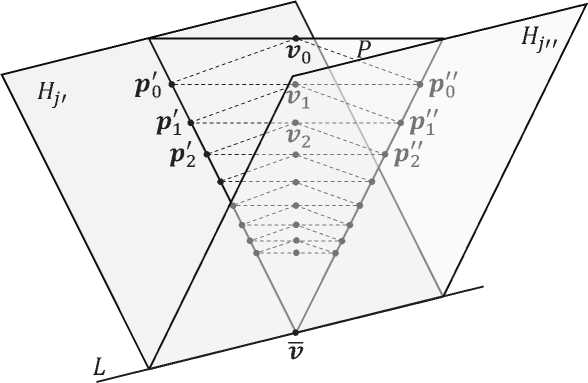
Рис. 3. Иллюстрация к доказательству утверждения 2 при n = 3

Доказательство. Зафиксируем произвольную точку \bfitv 0 \in \BbbR ⁿ . Рассмотрим линейное многообразие P , содержащее точку \bfitv 0 , и являющееся ортогональным дополнением к линейному многообразию L:

г о G P = L ^                                 (31)

Обозначим через v точку пересечения линейного многообразия L с его ортогональным дополнением P:

L n P = { г }

(см. рис. 3) . Построим ортогональную проекцию точки \bfitv 0 на гиперплоскость H j для произвольного j \in \scrJ :

Р о = “ II (М

В соответствии с леммой 1 имеем

“ H j (М G P.

Отсюда и из (24) следует, что

V 1 = ^( ^ о ) G P.

Это означает, что последовательность

{^{V k} = ^ ‘ ы}^

сходится к точке V пересечения линейного многообразия L с линейным многообразием P , то есть, P l ( v o ) = V . С другой стороны, в силу (31) имеем “ l ( v o ) = V . Следовательно

V x G R n : p _L ( x) = “ _L ( x ).

Утверждение доказано.

Процедура приближенного вычисления псевдопроекции на линейное многообразие представлена в виде алгоритма 1. Дадим краткий комментарий по шагам этого алгоритма. На шаге 2 счетчик итераций k устанавливается в значение ноль. Шаг 3 задает начальное приближение \bfitx 0 . Шаг 4 открывает итерационный цикл вычисления псевдопроекции. Шаги 5–8 для текущего приближения \bfitx k вычисляют сумму из правой части формулы (24) . 2024, т. 13, № 3                                                                     13

Алгоритм 1 Вычисление псевдопроекции p j ( ж )

Require: H i = { ж G R n |( a i , ж ) = b i } ; J С { 1,..	. ,m } ; J = 0 ; П H i = 0 i \in\scrJ
1:    function \bfitrho \scrJ ( \bfitx ) 2:      k :=0 3:      ж о := ж 4:     repeat 5:         £ :=0 6:             for i \in \scrJ do 7:               £ :=S + ( ( a i , ж к ) - b i ) a i /\\ a i \\2
8:         end for 9:          ж (к+1) := ж к - £/ |J| 10:         С тах : — 0	\triangleleft Максимальная невязка
11:             for i \in \scrJ do 12:                  C i : = || { a i , ж к +1 )     b i || 13:               if \xi i > \xi max then 14:                  С тах : — Ci 15:             end if 16:         end for 17:          k := k + 1 18:         until \xi max < \epsilon \xi	> Малый параметр e g > 0
19:       return \bfitx k

20: end function

Шаг 9 находит следующее приближение ж к₊р Шаги 10-16 определяют максимальную невязку \xi для нового приближения относительно всех гиперплоскостей H i , участвующих в вычислении. На шаге 17 счетчик итераций увеличивается на единицу. Шаг 18 проверяет условие выхода из итерационного цикла. Шаг 19 возвращает в качестве результата полученное приближение \bfitx k .

3.    Алгоритм движения по граням AlFaMove

В этом разделе мы опишем новый алгоритм AlFaMove (Along Faces Movement), представляющий собой численную реализацию метода поверхностного движения [9] . Алгоритм AlFaMove строит на поверхности допустимого многогранника путь из произвольной граничной точки U q G M И Г(М) до точки ж , являющейся решением задачи ЛП (1) . Перемещение по граням допустимого многогранника происходит в направлении наибольшего увеличения значения целевой функции. Путь, построенный в результате такого движения, называется оптимальным целевым путем.

В основе алгоритма AlFaMove лежит процедура D ( u ) вычисления вектора движения d по грани допустимого многогранника M из точки \bfitu в направлении максимального увеличения значения целевой функции. Процедура D ( u ) представлена в виде алгоритма 2. Схематично работа этого алгоритма изображена на рис. 4. Дадим краткий комментарий по шагам алгоритма 2. Шаги 2–7 строят множество \scrU , включающее в себя индексы всех гиперплоскостей H i , проходящих через точку \bfitu . На шаге 8 вектору направления движения \bfitd в качестве начального значения присваивается нулевой вектор. На шаге 9 значению це-14 Вестник ЮУрГУ. Серия «Вычислительная математика и информатика»

Алгоритм 2 Вычисление вектора движения d = D(u)

Require: H i = { ж E R n |( a i , ж ) = b i } ; u E Г(М)

• 1:    function \bfitD ( \bfitu )

• 2:    U := 0   >  U — множество индексов гиперплоскостей H i , проходящих через точку и

• 3:      for i = 1 .. .m do

• 4:          if ( a i , и ) = b i then

• 5:           U := UU{i}

• 6:         end if

• 7:     end for

• 8:      d : = 0

• 9:     f := -от                              > f — значение целевой функции f ( ж ) = ( с , ж )

• 10:       е _с := с /|| с ||

• 11:     v := и + 6 е _с                                           > Большой параметр 6 >  0

• 12:     for J E V(U ) \0 do            >  Р(U ) — множество всех подмножеств множества U

• 13:         W := P j ( v )

• 14:        d := w — и

• 15:          e _d := d /^ d ^

• 16:        if ( u + т e d) E M then                               > Малый параметр т > 0

• 17:            if ( с , и + т e d) > / then

• 18:                f ^: = ( с , и + те_а)

• 19:                  d) := d

• 20:             end if

• 21:         end if

• 22:     end for

• 23:       return \bfitd

• 24:    end function

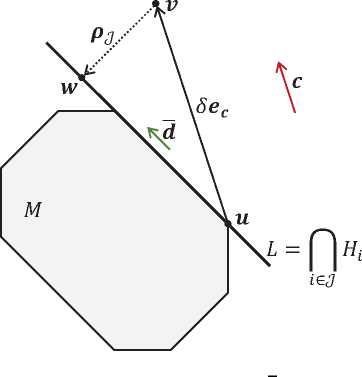
Рис. 4. Вычисление вектора направления движения \bfitd по грани линейного многообразия L левой функции f присваивается бесконечно малое число3 . На шаге 10 строится единичный вектор \bfite\bfitc, сонаправленный с вектором \bfitc. На шаге 11 строится точка \bfitv путем прибавления вектора \delta\bfite\bfitc к вектору \bfitu (см. рис. 4). Здесь \delta — «большой» положительный параметр: чем больше \delta, тем точнее будет вычислен вектор направления движения \bfitd. Однако при увеличении параметра 5 будет увеличиваться и время вычисления псевдопроекции pj(г) на шаге 13. Цикл for на шаге 12 перебирает все возможные комбинации индексов гиперплоскостей, проходящих через точку \bfitu. Каждой такой комбинации \scrJ соответствует линейное многообразие L = i\^H Hi, которое также проходит через точку и. Шаг 13 вычисляет точку \bfitw, выполняя псевдопроекцию точки \bfitv на линейное многообразие, соответствующее комбинации \scrJ . На шаге 14 вычисляется возможный вектор движения \bfitd по текущему линейному многообразию в направлении максимального увеличения значений целевой функции. Шаг 15 вычисляет единичный вектор \bfite\bfitd, сонаправленный с вектором \bfitd. Шаг 16 проверяет, что малое движение из точки \bfitu в направлении \bfitd не выходит за границы допустимого многогранника. Шаг 17, в свою очередь, проверяет, что значение целевой функции в точке (и + е^) превышает максимальное значение, полученное на предыдущих итерациях цикла for (шаг 12). В этом случае это значение запоминается как максимальное (шаг 18), а найденное направление присваивается вектору \bfitd (шаг 19). После того, как проверены все возможные комбинации, вектор \bfitd возвращается в качестве результата (шаг 23). Если ни одна комбинация не прошла проверку на шагах 16–17, то в качестве результата будет возвращен нулевой вектор. Это означает, что любое движение из точки \bfitu по поверхности допустимого многогранника не приводит к увеличению значения целевой функции.

Теперь мы готовы описать алгоритм движения по граням AlFaMove, решающий задачу ЛП (1). За основу мы берем алгоритм 1 из работы [9]. Реализация алгоритма AlFaMove на псевдокоде представлена в виде алгоритма 3. Прокомментируем шаги этого алгоритма. На шаге 1 вводится начальное приближение u(g). Это может быть произвольная граничная точка рецессивного многогранника ML, удовлетворяющая условию ug G М П Г(М).

Это условие проверяется на шаге 2. Для получения подходящего начального приближения может применяться алгоритм, реализующий стадию Quest апекс-метода [10] . Шаг 3 вычисляет начальный вектор движения d g . Для этого используется функция D ( - ), реа-

Алгоритм 3 Алгоритм движения по граням AlFaMove

Require: HI i = { х G ^{ a i , x ) <  b i } ; M = ^Q H i ; M = ^Q Hl i ; i Gl^ { a i , c ) >  0 i=i            ie!

• 1:    input U g

• 2:    assert U g G M П Г(М)

• 3:    d g := D ( u g )

• 4:    assert d g = 0

• 5:    k :=0

• 6:    repeat

• 7:      U k₊₁ := p ( U k , d k )

• ^{8:     d} k+1 ^: = ^D(u k +1 ⁾

• 9:      k := k + 1

• 10:    until d k = 0

• 11:    output \bfitu k                                                                             \triangleleft Решение задачи ЛП (1)

• 12:    stop

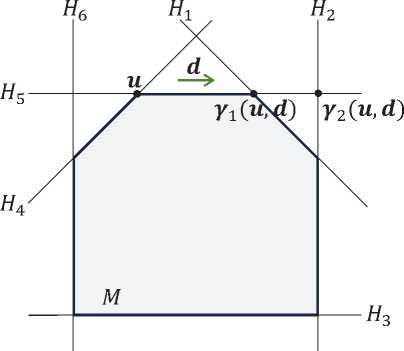
Рис. 5. Действие функции \bfitmu :

^ ( u , d ) = 7 1 ( u , d )

лизованная в алгоритме 2. Предполагается, что d o = 04. Это условие контролируется на шаге 4. На шаге 5 счетчик итераций к устанавливается в значение ноль. Шаг 6 открывает цикл repeat , выполняющий движение по граням допустимого многогранника до тех пор, пока очередной вектор движения \bfitd k не окажется нулевым вектором. Это означает, что последнее найденное приближение \bfitu k является решением задачи ЛП (1) . Шаг 7 в теле цикла вычисляет следующее приближение \bfitu k+1 с помощью вектор-функции \bfitmu (определение см. ниже). Шаг 8 вычисляет вектор движения \bfitd k+1 для вновь найденного приближения \bfitu k+1 . Шаг 9 увеличивает счетчик итераций к на единицу. Если последний вектор движения равен нулевому вектору, то на шаге 10 происходит выход из цикла repeat/until , после чего на шаге 11 выводятся координаты точки \bfitu _k в качестве решения задачи ЛП (1) . Шаг 12 завершает работу алгоритма AlFaMove.

Вектор-функция м(’), используемая на шаге 7, определяется следующим образом. Обо значим

Q = {i 6{ 1,...,m }| ( a i , и ) < b i Л ( a i , d) >  0 } .                     (32)

Тогда

^ ( u , d ) = arg min {| u — ж | | ж = 7 i ( u , d )} .                       (33)

i \in\scrQ

Здесь 7 i ( u , d ) обозначает вектор-функцию, вычисляющую косоугольную проекцию точки и на гиперплоскость H i по направлению d :

• 7 i ( и , d )= и — ^{( a} i , ^{u )}- b i d . ( a i , d )

Действие функции \bfitmu проиллюстрировано на рис. 5. В соответствии с рисунком гиперплоскости H 4 и H 5 не удовлетворяют неравенству ( a i , и ) < b i в (32) . Гиперплоскости H 3 и Н б не удовлетворяют неравенству ( a i , d ) >  0 в (32) . Таким образом, Q = { 1,2 } . Так как | u — 7 1 ( u , d ) | <  | и — 7 2 ( и , d ) | , то ^ ( и , d) = 7 1 ( и , d ).

• ⁴Равенство вектора \bfitd0 нулевому вектору означает, что точка \bfitu0 является решением задачи ЛП (1).

4.    Параллельная версия алгоритма AlFaMove

Сходимость алгоритма 3 к решению задачи ЛП (1) за конечное число итераций обеспечивается следующей теоремой.

Теорема 1. (Сходимость алгоритма AlFaMove) Пусть допустимый многогранник M задачи ЛП (1) является ограниченным непустым множеством. Пусть ж — решение задачи ЛП (1) . Тогда последовательность приближений { u k } K ₌₁ , генерируемых алгоритмом 3, является конечной (K < + то ), и ( с , и к ) = ( с , ж ) , то есть и к является решением задачи ЛП (1) .

Доказательство. Обозначим через dAiFaMove вектор dk+±, вычисляемый на шаге 8 алгоритма 3. В соответствии с шагами 13, 14 алгоритма 2 имеем dAlFaMove = pj (v) - U.

Согласно утверждению 2 отсюда следует dAiFaMove = Kj(v) - U,                             (34)

где K j ( v ) обозначает ортогональную проекцию точки v на линейное многообразие L = P|j_ej H i . В соответствии с утверждением 1 это означает, что вектор d AiFaMove однозначно задает направление максимального увеличения целевой функции f( ж ) задачи (1) . А это, в свою очередь, означает, что алгоритм 3 является численной реализацией метода поверхностного движения [9] , то есть последовательности приближений \bfitu ^k _{AlF aM ove} и \bfitu ^k _SMM , генерируемые алгоритмом 3 из настоящей статьи и алгоритмом 1 из [9] соответственно, совпадают. Таким образом сходимость алгоритма AlFaMove непосредственно следует из сходимости алгоритма поверхностного движения, гарантируемой теоремой 1 из статьи [9] .

Наиболее ресурсоемкой операцией, используемой в алгоритме AlFaMove (алгоритм 3) , является операция вычисления вектора движения, выполняемая в цикле на шаге 8. При решении больших задач ЛП она занимает более 90% процессорного времени. Это объясняется тем, что функция вычисления вектора движения D (-), реализованная в виде алгоритма 2, использует в цикле на шаге 13 операцию псевдопроектирования, заключающуюся в последовательном применении отображения ^( - ), задаваемого формулой (24) , к исходной точке (см. алгоритм 1, реализующий вычисление псевдопроекции). Известно, что в случае больших задач ЛП проекционный метод может потребовать значительных временных затрат [13] . Кроме того, следует отметить, что алгоритм 2 в цикле на шаге 12 перебирает все непустые подмножества множества \scrU , включающего в себя индексы гиперплоскостей, проходящих через точку \bfitu . Если, например, через точку проходит 30 гиперплоскостей, то у нас получится 2 ³⁰ - 1 = 1 07 3 741 823 непустых подмножества. Перебор такого количества подмножеств потребует суперкомпьютерных мощностей. Потому мы разработали параллельную версию алгоритма AlFaMove, представленную в виде алгоритма 4.

Параллельный алгоритм 4 построен на основе модели параллельных вычислений BSF [14] , ориентированной на кластерные вычислительные системы. Модель BSF использует схему распараллеливания «мастер–рабочие» и требует представление алгоритма в виде операций над списками с использованием функций высшего порядка Map и Reduce .

Алгоритм 4 Параллельная версия алгоритма AlFaMove

мастер	l -тый рабочий (l = 0,..., L — 1)
1:    input n, m, A, b , u 0 2:    k :=0	1: input n, m, A, \bfitb , \bfitc 2:
3:    repeat 4:      Broadcast \bfitu k 5: 6: 7: 8: 9:	3:    repeat 4:     RecvFromMaster \bfitu k 5:      U : = [] 6:      for i = 1 .. .m do 7:          if { a i , U k ) = b i then 8:              U : = U -+[i] 9:         end if
10:	10:     end for
11:	11:     K :=2^\ — 1
12:	12:     L := NumberOfWorkers
13:	13:      ^ map ( l ) : = [lK/L, • • • , (l + 1)K/L - 1]
14:	14:      £ reduce ( l ) — Map (F U k , £ map ( l ) )
15: 16:      Gather \scrL reduce 17:     ( d k ,f k ) := Reduced, deduce) 18:     if d k = 0 then 19:         exit := true 20:      else 21:          U k+1 : M ( u k , d k ) 22:          k := k + 1 23:          exit := false 24:     end if 25:     Broadcast exit 26:    until exit 27:    output \bfitu k , f k 28:    stop	15:     ( d i ,f i ) := Reduced, С^®) 16:     SendToMaster ( d l , f l ) 17: 18: 19: 20: 21: 22: 23: 24: 25:    RecvFromMaster exit 26:    until exit 27: 28: stop

В качестве второго параметра функции высшего порядка Map в алгоритме 4 используется список £ _map = [1,... ,K], содержащий порядковые номера всех подмножеств множества U , за исключением пустого. Здесь K = 2 |^| — 1. В качестве первого параметра фигурирует параметризованная функция

F _w : { 1,...,K } - R n х R , определенная следующим образом:

F _u (j ) = ( d j ,f j );

{ e _d , if ( и + т e _d ) G M Л ( c , w ) >  ( c , и );

0 , if ( и + т e d ) G M V ( c , w ) <  ( c , и );                          (35)

{ ( c , и + e d ), if ( и + т e d ) G M Л ( c , w ) > ( c , u );

—от,         if (и + тed) / M V (c, w) < (c, u), где w = pjv + ^c/llcID                          (36)

и

\bfitw - \bfitu

^{\bfite \bfitd}             | \bfitw - \bfitu |

Семантика функции F _w ( • ) однозначно определяется алгоритмом 2. Функция а( - ), используемая в формуле (36) , отображает натуральное число j G { 1,..., K } в j -тое подмножество множества элементов списка scrU следующим образом. Число j преобразуется в двоичное представление, состоящее из |scrU | разрядов. Каждому разряду соответствует индекс гиперплоскости из списка scrU в естественном порядке. Если разряд содержит единицу, то соответствующий индекс входит в подмножество a(j ), если — ноль, то не входит. Например, пусть через точку и проходят гиперплоскости H 2 , H 4 , H 7 , H 9 . В этом случае U = [2, 4, 7, 9] и K = 2 4 — 1 = 15, то есть из множества элементов списка U может быть сформировано 15 различных непустых подмножеств. Найдем, например, пятое подмножество. Функция С0 преобразует число 5 в двоичную запись из 4-x разрядов 0101 и возвращает в качестве результата подмножество { 4, 9 } . Таким образом функция высшего порядка Map (F _u , £ _map) преобразует список £ _map номеров подмножеств в список пар ( d j , f j ):

Map (F _u , £ map ) = [F , (1),..., F _u (K)] = [( d f),..., ( d K ,f _K )] .

Здесь d j (j = 1,..., K ) является единичным вектором движения, а fj — значение целевой функции, которое достигается в точке и + d j .

Обозначим через scrL _reduce список пар, генерируемый функцией высшего порядка Map :

deduce = Map (F _u , £ map ) = [( d i , f i ),..., ( d K , f K )] .

Определим бинарную ассоциативную операцию ф : Rn x X - Rn x R, являющуюся первым параметром функции высшего порядка Reduce:

\bfitd ^\prime ,f ^\prime oplus \bfitd ^\prime\prime ,f ^\prime\prime

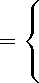
(d',f ' ) , (d",f ") ,

еслиf ' >  f "; если f ^\prime < f ^\prime\prime .

Функция высшего порядка Reduce редуцирует список пар scrL _re d _uce к одной паре путем последовательного применения операции oplus ко всем элементам списка:

Reduce (ф, ^reduce ) = (di,fi) ф ... ф (dK, fK) = (dj, fj ), где согласно (37)

j ' ^{= arg} 1 jK f j •

Параллельная работа алгоритма 4 организована по схеме «мастер–рабочие» и включает в себя L + 1 процесс: один процесс-мастер и L процессов-рабочих. Процесс-мастер осуществляет общее управление вычислениями, распределяет работу между процессами– рабочими, получает от них результаты и формирует итоговый результат. Для простоты будем предполагать, что количество подмножеств K кратно количеству рабочих L. На шаге 1 мастер вводит исходные данные задачи ЛП и начальную точку U q . На шаге 2 мастер устанавливает счетчик итераций k в значение ноль. Шаги 3–26 реализуют основной цикл repeat/until , вычисляющий решение задачи ЛП (1) . На шаге 4 мастер рассылает текущее приближение \bfitu k всем рабочим. На шаге 16 он получает от рабочих частичные результаты, которые на шаге 17 редуцируются в пару ( d k , f k ). Если на шаге 18 выполняется условие d k = О , то решение найдено (мы предполагаем d o = О ). В этом случае на шаге 19 мастер присваивает логической переменной exit значение true . Если d k = О , то мастер на шаге 21 вычисляет следующее приближение U k₊i , увеличивает на шаге 22 счетчик итераций k на единицу и на шаге 23 присваивает логической переменной exit значение false . На шаге 25 мастер рассылает всем рабочим значение логической переменной exit . Если логическая переменная exit принимает значение «истина», цикл repeat/until завершается на шаге 26. На шаге 27 мастер выводит в качестве результата последнее приближение \bfitu k и оптимальное значение целевой функции f _k . Шаг 28 завершает работу процесса–мастера.

Все рабочие выполняют один и тот же код, но над различными данными. На шаге 1 1-тый рабочий (1 = 1,... ,L) вводит исходные данные задачи ЛП. Цикл repeat/until рабочего (шаги 3-26) соответствует циклу repeat/until мастера. На шаге 4 l -тый рабочий получает от мастера текущее приближение U k . Затем он формирует подсписок £ _map ( i ) своих порядковых номеров подмножеств для последующей обработки (шаги 5–13). Подсписки различных рабочих не пересекаются:

l' = I" О £ map ( l > ) = £ map ( l" ) ,                                ⁽³⁸⁾

а их конкатенация дает полный список:

^ map = £ map (0) ⁺ • • • ⁺ ^ map ( L - l) .

На шаге 14 рабочий вызывает функцию высшего порядка Map, которая, в свою очередь, применяет параметризованную функцию F ^ k , определенную формулами (35) , ко всем элементам подсписка £ _ma p ( i ) , формируя на выходе подсписок пар C reducey ) . Этот подсписок на шаге 15 редуцируется рабочим в единственную пару ( d i , f i ) с помощью функции высшего порядка Reduce , которая последовательно применяет бинарную операцию \oplus , определенную по формуле (37) , ко всем элементам подсписка £ _re d _uce ( i ) . Результат пересылается мастеру на шаге 16. На шаге 25 рабочий получает от мастера значение логической переменной exit . Если эта переменная принимает значение true , то рабочий процесс завершается. В противном случае продолжает выполняться цикл repeat/until . Операторы обмена Broadcast , Gather , RecvFromMaster и SendToMaster обеспечивают неявную синхронизацию работы процесса–мастера и процессов–рабочих.

5.    Вычислительные эксперименты

Мы реализовали параллельную версию алгоритма AlFaMove на языке C++ с использованием программного BSF-каркаса [15], базирующегося на модели параллельных вычислений BSF [14]. BSF-каркас инкапсулирует все аспекты, связанные с распараллеливанием программы на основе библиотеки MPI. Исходные коды параллельной реализации алгоритма AlFaMove решения задач ЛП свободно доступны в репозитории GitHub по адресу Разработанная программа была протестирована на большом количестве задач ЛП, взятых из различных источников. Все эти задачи в формате MTX [16] доступны по адресу Set-of-LP-Problems. В качестве тестов мы также использовали искусственные задачи, полученные с помощью генератора случайных задач ЛП FRaGenLP [17]. Эти задачи доступны по адресу main/Rnd-LP. Мы не смогли протестировать реализацию AlFaMove на задачах из репозитория Netlib-LP [18], так как во всех этих задачах количество гиперплоскостей, проходящих через начальную точку \bfitu0 , превышало число 30, что соответствует количеству возможных комбинаций, равному 1 073 741 824. Массивы таких размеров не допускаются доступными нам компиляторами C++.

С помощью разработанной программы мы исследовали масштабируемость алгоритма AlFaMove. В экспериментах мы использовали параметризованную задачу ЛП «гиперкуб с отсеченной вершиной», для которой размерность пространства n является параметром. Ограничения этой задачи содержат 2п +1 неравенств следующего вида:

' xi

Х2

. . ^.

xn<

Х 1 +  Х 2       •••   +   X n <  200(n - 1) + 100

x1 > 0,  x2 > 0,  •••  ,xn

Градиент целевой функции задается вектором c = (1,2,...,n).

Задача предполагает нахождение максимума целевой функции и имеет единственное решение в точке (100, 200,..., 200) со значением целевой функции, равным 100(n2 + n — 1). Для произвольного n эта задача может быть получена в формате MTX с помощью генератора FRaGenLP, если в качестве количества случайных неравенств задать 0. Эти задачи ЛП для различных n доступны по адресу Set-of-LP-Problems/tree/main/Rnd-LP под именами lp_rnd-0, где в качестве указана размерность пространства. Вычислительные эксперименты проводились на суперкомпьютере «Торнадо ЮУрГУ» [19], характеристики которого представлены в табл. 1. Все вычисления выполнялись с двойной точностью, при которой число с плавающей точкой занимает в оперативной памяти 64 бита.

В первой серии экспериментов исследовалась зависимость ускорения и эффективности распараллеливания алгоритма AlFaMove от количества используемых процессорных узлов кластера при решении задач «гиперкуб с отсеченной вершиной». Результаты этих экспериментов представлены на рис. 6. В данном контексте ускорение a(L) определялось как отно-22 Вестник ЮУрГУ. Серия «Вычислительная математика и информатика»

Таблица 1. Характеристики кластера «Торнадо ЮУрГУ»

Параметр Значение Количество процессорных узлов Процессоры Число процессоров на узел Память на узел Соединительная сеть Операционная система 480 Intel Xeon X5680 (6 cores, 3.33 GHz) 2 24 GB DDR3 InfiniBand QDR (40 Gbit/s) Linux CentOS шение времени T(1) решения задачи на конфигурации с узлом-мастером и единственным узлом-рабочим ко времени T(L) решения той же задачи на конфигурации с узлом-мастером и L узлами-рабочими:

«»- S',

Эффективность распараллеливания fl (L) вычислялась по формуле

^(L)-

T (1)

L • T(L) ’

Вычисления проводились для размерностей 16, 18 и 20. Число ограничений соответственно составило 33, 37 и 41. В качестве начальной точки всегда выбиралась вершина допустимого многогранника со следующими координатами:

Х 1 -0, ... x _n / 2 -0, X n/2+1 - 200,   ... x _n - 200.               (42)

Эксперименты продемонстрировали хорошую масштабируемость алгоритма AlFaMove на задачах «гиперкуб с отсеченной вершиной», начиная с размерности n - 18. В этом случае алгоритм демонстрировал ускорение, близкое к линейному. На меньших размерностях затраты на обмены и латентность начинают превалировать над вычислительными затратами, что приводит к резкому уменьшению границы масштабируемости алгоритм а5. Для

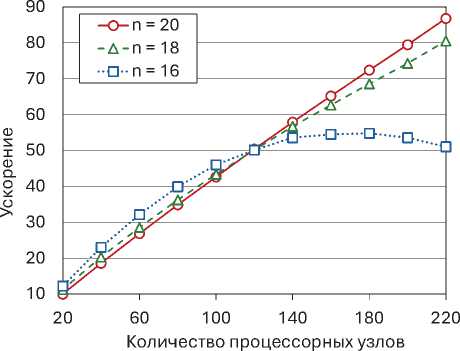
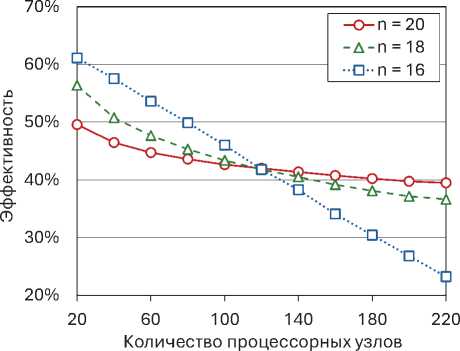
Рис. 6. Ускорение и эффективность распараллеливания алгоритма AlFaMove

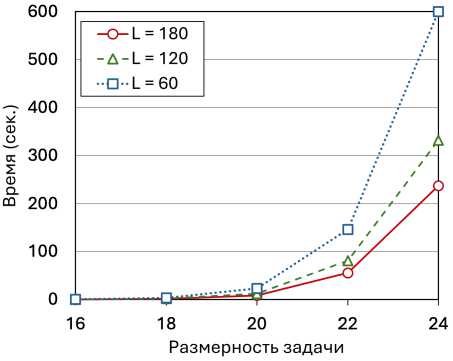
Рис. 7. Зависимость времени работы AlFaMove от размерности задачи на различных многопроцессорных конфигурациях ( L — количество рабочих узлов)

n = 16 эта граница оказалась равной 180 узлам. Эксперименты также показали, что с увеличением размерности задачи эффективность распараллеливания на малом количестве процессорных узлов (меньше 120) падает. Однако, при большем количестве процессорных узлов наблюдается обратная тенденция. Так, для размерности n = 16 эффективность распараллеливания на 20 процессорных узлах составила 61%, после чего снизилась до 23% на 220 узлах. При этом, для n = 20 эффективность распараллеливания оказалась равной 50% и 40% соответственно.

В следующей серии экспериментов исследовалась зависимость времени вычислений от размерности задачи «гиперкуб с отсеченной вершиной» на различных многопроцессорных конфигурациях с количеством рабочих узлов L = 60, L = 120 и L = 180. Результаты этих экспериментов представлены на рис. 7. Размерность варьировалась от n = 16 до n = 24 с шагом 2. Для размерности n = 24 каждый из списков \scrL _map и \scrL _reduce включал в себя 16 777 215 элементов. Это — максимальный размер, допускаемый используемым компилятором. В качестве начальной точки всегда выбиралась вершина допустимого многогранника с координатами (42) . На всех исследуемых конфигурациях эксперименты показали экспоненциальный рост времени вычислений с увеличением размерности задачи. Однако, конфигурации с б´ольшим количеством рабочих узлов демонстрировали существенно меньшее время работы алгоритма AlFaMove.

В третьей серии экспериментов мы исследовали поведение алгоритма AlFaMove на кубе Кле—Минти (Klee—Minty), представляющем собой параметризованную задачу ЛП с размерностью пространства в качестве параметра. Область допустимых решений этой задачи представляет собой гиперкуб с перекошенными углами и может быть задана следующей системой неравенств:

^\left\{ x 1                                                                                                                                                                   \leqslant 5

4x 1 + x 2                                                            \leqslant 25

8x 1 + 4x 2 + x 3                                    \leqslant 125

. . .

2n xi +  2n-1 X2  • • •  + 4xn-i  + Xn  < 5n x1 \geqslant 0,        x2 \geqslant 0,         \cdot \cdot \cdot         , xn \geqslant 0.

Градиент целевой функции задается вектором с = (2n-1

2 n - 2

...,2,1 .

Задача предполагает нахождение максимума целевой функции и имеет единственное решение в точке (0, ... , 0, 5 ⁿ ) со значением целевой функции, равным 5 ⁿ . Кле и Минти в статье [20] показали, что в случае, когда начальной вершиной является центр координат, классический симплекс-метод при решении этой задачи посещает все 2 ⁿ вершин, делая 2 ⁿ - 1 итераций. Известно, что большинство оптимизационных алгоритмов демонстрируют плохую производительность применительно к кубу Кле—Минти. Мы применили алгоритм AlFaMove для решения кубов Кле—Минти размерности от 5 до 9. Результаты экспериментов, приведенные в табл. 2, показывают, что алгоритм AlFaMove во всех случаях находил решение за 2n - 1 итераций, в то время, как симплекс-метод совершал 2 ⁿ - 1 итераций.

Таблица 2. Эксперименты с кубами Кле—Минти

Размерность	AlFaMove				Simplex
	Граница масшт-ти	Время (сек.)	Относит. погреш-ть	Кол-во итераций	Кол-во итераций
5	10	0.2	0.9 • 10 - 12	9	31
6	15	2	0.2 • 10 - 12	11	63
7	20	13	0.8 • 10 - 11	13	127
8	25	126	0.8 • 10 - 11	15	255
9	30	1445	0.2 • 10 - 10	17	511

Относительная погрешность вычислялась по формуле

\delta=

f exact ^- f approx f exact

где fexact — точное максимальное значение целевой функции, fapprox — значение, вычисленное алгоритмом AlFaMove. Подсчет итераций симплекс-метода производился с помощью онлайн калькулятора, доступного по адресу simplex-method-calculator. Эксперименты также показали, что порог масштабируемости алгоритм AlFaMove на кубах Кле—Минти рос линейно с ростом размерности. При этом одновременно наблюдался экспоненциальный рост времени вычислений.

Заключение

В статье представлен алгоритм AlFaMove, являющийся численной реализацией метода поверхностного движения для решения задач линейного программирования. Ключевой особенностью этого метода является построение оптимального пути на поверхности допустимого многогранника от начальной точки к решению задачи линейного программирования. Под оптимальным путем понимается путь по поверхности допустимой области в направлении максимального увеличения значений целевой функции. Практическая значимость предложенного метода состоит в том, что он открывает возможность применения искусственных нейронных сетей прямого распространения для решения нестационарных многомерных задач линейного программирования в режиме реального времени.

Теоретической основой алгоритма AlFaMove является операция построения псевдопроекции на линейные многообразия, которые формируют грани допустимого многогранника. Псевдопроекция реализуется на основе фейеровского процесса и является обобщением понятий ортогональной проекции на линейное многообразие и метрической проекции на выпуклое множество. В случае грани, образуемой гиперплоскостью, псевдопроекция сводится к ортогональной проекции. Доказано, что путь по гиперплоскости, построенный с помощью градиента целевой функции и ортогональной проекции, является оптимальным. Приведен алгоритм проекционного типа для построения псевдопроекции на линейные многообразия меньших размерностей, образуемые пересечением гиперплоскостей. Доказано, что в этом случае псевдопроекция совпадает с ортогональной проекцией. Представлено формализованное описание алгоритма AlFaMove, строящего оптимальный путь на поверхности допустимого многогранника. В основе алгоритма AlFaMove лежит процедура вычисления вектора движения по грани допустимого многогранника из точки текущего приближения в направлении максимального увеличения значения целевой функции. Дано формализованное описание этой процедуры.

Алгоритмы проекционного типа характеризуются низкой скоростью сходимости, зависящей от углов между гиперплоскостями, образующими линейное многообразие. Также отмечено, что при вычислении вектора движения возникает переборная задача комбинаторного типа, имеющая высокую пространственную и временную сложность. Представлена параллельная версия алгоритма AlFaMove, ориентированная на кластерные вычислительные системы. Параллельная версия реализована на языке C++ с использованием программного BSF-каркаса, основанного на модели параллельных вычислений BSF. Проведены эксперименты по исследованию масштабируемости алгоритма AlFaMove на кластерной вычислительной системе. Вычислительные эксперименты показали, что задача линейного программирования с 24 переменными и 49 ограничениями демонстрирует ускорение близкое к линейному на 320 процессорных узлах кластера. Задачи большей размерности приводили к ошибке компилятора, связанной с превышением максимального допустимого размера массивов.

В качестве направлений дальнейших исследований выделим следующие. Мы планируем разработать новый, более эффективный метод построения пути на поверхности допустимого многогранника, приводящего к решению задачи линейного программирования. Основная идея состоит в сокращении перебираемых комбинаций гиперплоскостей при определении направления движения. Это может быть достигнуто, если мы ограничимся перемещениями только по ребрам многогранника (линейным многообразиям размерности один). Проблема пространственной сложности может быть решена путем перехода к стохастическим методам выбора направления движения.

Исследование выполнено при финансовой поддержке РНФ (проект № 23-21-00356).