Численная схема CSPH-TVD: моделирование фронта ударной волны

1.    Моделирование сверхзвуковых течений

Необходимость моделирования ударных волн возникает при рассмотрении широкого круга задач в аэродинамике, теории взрыва, астрофизике [3; 6], в технических приложениях (например, связанных со сваркой, взрывом, при проведении строительных работ). Точность описания фронта ударной волны часто используют в качестве универсального теста, определяющего качество численных алгоритмов интегрирования уравнений газодинамики.

В работе [4] была предложена оригинальная численная схема cSPH-TVD (combined Smoothed Particle Hydrodynamics – Total Variation Diminishing) для моделирования динамики поверхностных вод на основе модели Сен-Венана. Наиболее существенным свойством разработанной в [4] численной схемы является устойчивый сквозной счет нерегулярных или разрывных профилей рельефа дна и нестационарных границ «вода — сухое дно».

В данной работе проведено обобщение численной схемы cSPH-TVD на случай полной системы уравнений газодинамики в одномерном приближении. Предложенный подход позволяет проводить устойчивый сквозной счет астрофизических течений, содержащих нестационарные границы «газ — вакуум» [1]. В основе алгоритма лежит последовательное применение лагранжева и эйлерова подходов для решения уравнений газодинамики (рис. 1). В данной работе сделан акцент на исследование устойчивости и точности получаемых численных решений, содержащих сильные ударные волны.

2.    Основные уравнения

Будем исходить из интегральных законов сохранения массы, импульса и энергии для сплошной среды. Запишем систему уравнений газодинамики в интегральной форме при отсутствии внешних сил:

dt W^L=0,

-d [ pudL = - [ ^dL,(2)

dt Lup)              L(t) дх d             r dSupl dt ЦLu., ax , где L(t) — объем «жидких» частиц в одномерном приближении, деформирующийся в процессе движения произвольным образом; ρ — плотность среды; u — скорость газа; е = p(|u|2/2 + в) — полная энергия газа; в — удельная внутренняя энергия; р — изотропное давление. Система уравнений (1)–(3) замыкается уравнением состояния идеального газа в = р / [ (y — 1) р ] , где Y — показатель адиабаты. Для дальнейшего описания метода представим систему уравнений (1)–(3) в дифференциальной форме:

др + д^) = 0 ∂t ∂x

д (ри)   д (pu ^      др

∂t ∂x       ∂x , де   д (ue)     д (up)

∂t ∂x       ∂x

Далее будем использовать только безразмерные величины: р = р/ро, U = u/u0, е = = е/ео, р = р/ро, где ро, uo = xo/tg, eg, pg = (y — 1)(ео — РоU2/2) — характерные значения плотности, скорости, энергии и давления; хо — длина расчетной области; t0 — характерное время рассматриваемых процессов.

3.    Численный алгоритм cSPH-TVD

Воспользуемся стандартными процедурами дискретизации сплошной среды, применяемыми в численных схемах, основанных на лагранжевом и эйлеровом подходах. Покроем расчетную область равномерной эйлеровой (неподвижной) сеткой с пространственным шагом h и поместим в центры эйлеровых ячеек лагранжевы (подвижные) «жидкие» частицы. Введем временные слои t _n с неравномерным шагом τ _n . Таким образом, после дискретизации любую величину, входящую в исходные гидродинамические уравнения, можно представить в виде A(x, t) ^ A(x i ,t n ) = А П , где i — пространственный индекс; n — индекс временного слоя. Число ячеек и частиц равно N . Рассмотрим отдельно каждый из этапов метода.

На лагранжевом этапе определяется изменение характеристик и положений «жидких» частиц под действием сил газодинамического давления (рис. 1). На данном этапе применяется модифицированный SPH-подход [8]. Для описания динамики «жидких» частиц представим систему интегральных уравнений газодинамики (1)–(3) в консервативной лагранжевой форме. Определив средние значения величин р = (р, pu, е) внутри ячейки h^ii =

1 / h Lm€)

ϕ dL, получим:

d h q i _i

..■    = F i ,

hρii hq ii =     hpuii    , heii

F i =

/

I

-

h ξ i i

∂ξ

\

-

¹ №. de 2 h^ei - u i dx

∂x _i

-

2 h e ) ,

d«u)

∂x i

где

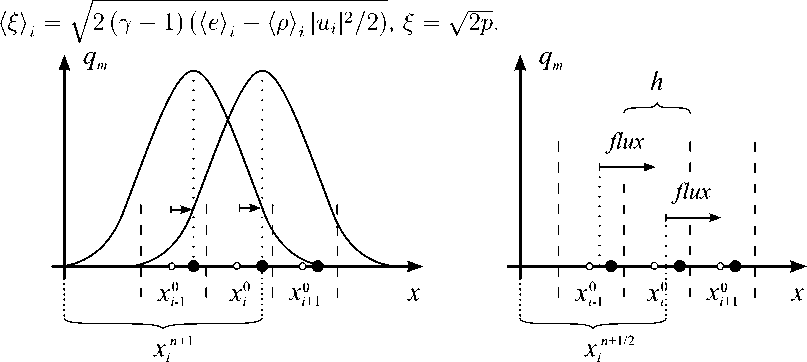
Рис. 1. На лагранжевом этапе (слева) определяется изменение характеристик «жидких» частиц, обусловленное действием на них сил газодинамического давления. На эйлеровом этапе (справа) вычисляются потоки массы, импульса и энергии, обусловленные перемещением жидкости через границы ячеек. Положение х П⁺¹ соответствует координате лагранжевой «жидкой» частицы, положение х 0 — центру эйлеровой ячейки

Для аппроксимации пространственных производных, входящих в уравнение (7), будем использовать модифицированный SPH-подход со сглаживающим ядром W [4]:

^ = X «>_t »c ₍

∂x          k ∂x i k=i-1           i

-

x k I ) ,

где W = hW . В качестве сглаживающего ядра, удовлетворяющего условию нормировки ∞

2п J sW(s)ds = 1, где s = | x i — x k | /h, может быть использован кубический сплайн 0

Монагана [8]:

W = A w

1 — 3 s ² + 3 s ³ , „ 2 4 , 4(2 — s) 3 ,

0 <  s <  1;

I ^{0 ,}

1 < s <  2; , 2 < s.

где A w = 2 / (3h) — весовой коэффициент. Для численного интегрирования по времени уравнения (7) запишем рекуррентные соотношения, используя алгоритм «предиктор— корректор». На шаге «предиктор» вычисляем значения h q i _i и x _i в момент времени t n+1/2 = t n + ^T n ^{/ 2}:

( n+1/2        n\

^P + Ш . (10)

h ρ i _i              h^ρi i

На шаге «корректор» вычисляем значения h q i i и x i в момент времени t n+1 = t n + т _п с учетом рассчитанных ранее значений этих величин на временном слое t _n+1 / ₂ :

h q Г¹ = h q ) П + т „ F i ( h q i " ^+1/2 ,x ^n+1/2) , x " ⁺¹ = x + ^ j + Ш') . (11)

² V hPi i          ^{h P}i i

Для устойчивости численной схемы на лагранжевом этапе необходимо, чтобы за время интегрирования τ _n частица не вышла за пределы ячейки.

На эйлеровом этапе вычисляются потоки массы, импульса и энергии, обусловленные перемещением жидкости через границы ячеек, в момент времени tn+1/2 = tn + тп/2 (рис. 1). На данном этапе применяется модифицированный TVD-подход, предложенный Хартеном [5], и приближенное решение задачи Римана. Разность втекающих и вытекающих в ячейки потоков позволяет определить изменения характеристик «жидких» частиц, рассчитанных на предыдущем этапе в момент времени tn+1 = tn + тп. Представим систему уравнений (4)–(6) в консервативной эйлеровой форме при отсутствии сил газодинамического давления:

∂q  ∂G

+    = 0,

∂t ∂x где G = q• и — потоки массы, импульса и энергии (см. (7)). Применив стандартную процедуру конечно-разностной аппроксимации к уравнению (12), для i-й ячейки получим соотношение:

q ? ⁺¹ =

n+1   Tn ( n+1/2 n+1/2 \ q ii       h Gi+1/2 - Gi-1/2 ,

где значения h q i ? ⁺¹ вычисляются на лагранжевом этапе по формулам (11), а значения n+1/2 n+1/2

потоков на границах ячеек G _i ± ₁ / ₂ = G q _i ± ₁ / ₂ ) находятся из приближенных решений задачи Римана с использованием метода Лакса — Фридрихса или Хартена — Лакса — ван Лира [11]. Для подавления нефизических осцилляций и обеспечения монотонности профилей сеточных величин на потоки G _i ⁿ _± ⁺ ₁ ¹ _/ ^/ ₂ ² накладывается функция-ограничитель [10]. Для устойчивости численной схемы на эйлеровом этапе необходимо, чтобы за время интегрирования τ _n возмущения не распространились на расстояние, превышающее размер ячейки.

Затем определяется изменение интегральных характеристик лагранжевых «жидких» частиц, обусловленное их потоками через границы эйлеровых ячеек. После чего «жидкие» частицы помещаются в исходное положение — в центры ячеек.

Временной шаг τ n для алгоритма cSPH-TVD с учетом требований устойчивости схемы на лагранжевом и эйлеровом этапах должен определяться из условия:

т _п = K min

h h

2" i u ni , л тах

где Xmax = тах(|и?| + an — максимальная скорость возмущений; an — адиабатическая i скорость звука; 0 < K < 1 — число Куранта.

4.    Результаты моделирования

Применим описанную численную схему к решению задачи Римана для уравнений газодинамики. Зададим начальные условия с левой границы от разрыва ρ L = 1, u L = 0, p L = 1 000 и с правой границы от разрыва ρ R = 1, u R = 0, p R = 0.01, показатель адиабаты γ = 5/3. Данный тест применяется для оценки устойчивости численной схемы при моделировании сильных ударных волн [12]. Решение состоит из сильной ударной волны, контактной волны и левой волны разрежения. Перепад давления на фронте ударной волны составляет p ∗ /p R = 46 000, что может нарушить используемые приближения идеального газа, но для оценки устойчивости численной схемы данный тест представляет значительный интерес. Результаты численного моделирования сравним с точным решением задачи Римана. Так как для уравнений газодинамики не существует точного решения, применим итерационную численную схему, позволяющую получить решение с необходимой точностью. На рисунках 2–5 представлены профили давления и плотности в момент времени t = 0.012 для N = 300, точное решение показано сплошной линией, численные решения показаны символами.

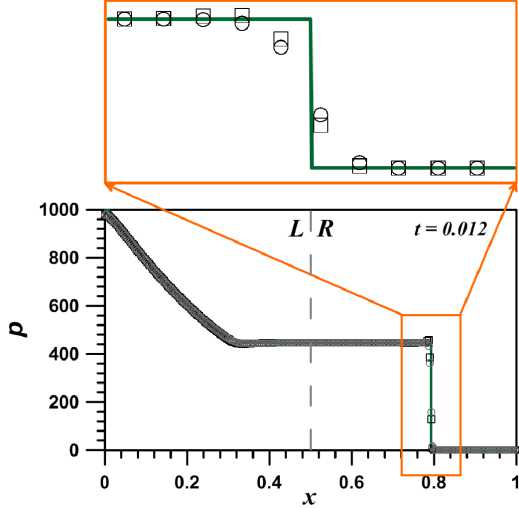
Рис. 2. Профиль давления, полученный c применением приближенных решений задачи Римана: метод Лакса — Фридрихса (кружки) и метод HLL (квадраты). Точное решение показано сплошной линией. На врезке изображена структура ударной волны

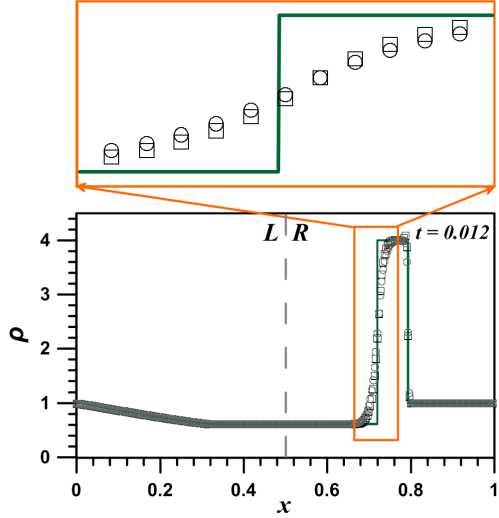
Рис. 3. Профиль плотности, полученный c применением приближенных решений задачи Римана: метод Лакса — Фридрихса (кружки) и метод HLL (квадраты). Точное решение показано сплошной линией. На врезке изображена структура контактной волны

На рисунках 2, 3 представлены профили давления и плотности, полученные с применением приближенных решений задачи Римана [2]: кружки соответствуют методу Лакса — Фридрихса , квадраты — методу Хартена — Лакса — ван Лира (HLL). Алгоритм, основанный на приближенном решении Лакса — Фридрихса , позволяет получить наиболее монотонный профиль. При использовании метода HLL возникают незначительные возмущения на фронте ударной волны.

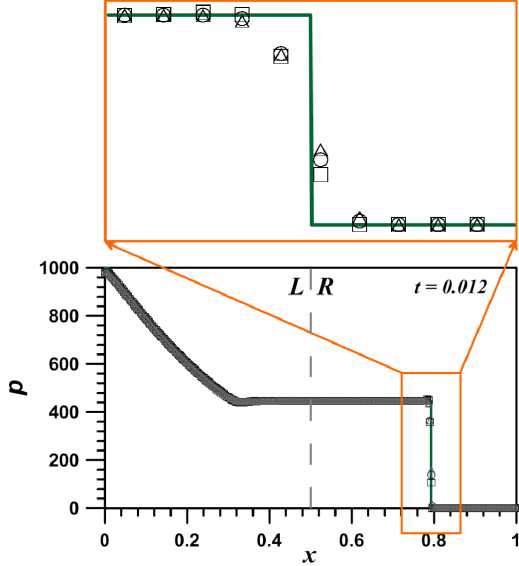
Рис. 4. Профиль давления, полученный с применением различных функций-ограничителей потоков: minmod (треугольники), ограничитель ван Альбады (кружки), ограничитель ван Лира (квадраты). Точное решение показано сплошной линией. На врезке изображена структура ударной волны

О 0.2       0.4       0.6       0.8        1

X

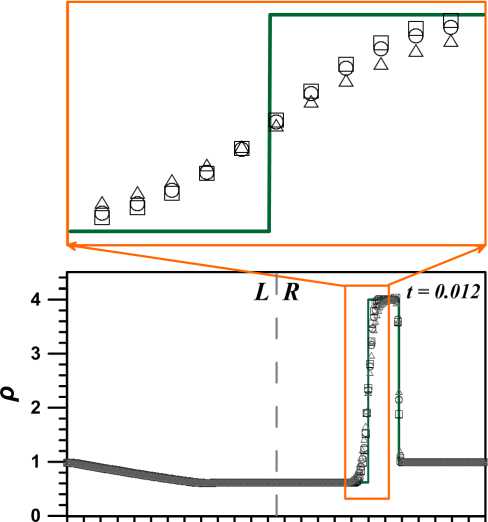
Рис. 5. Профиль плотности, полученный с применением различных функций-ограничителей потоков: minmod (треугольники), ограничитель ван Альбады (кружки), ограничитель ван Лира (квадраты). Точное решение показано сплошной линией. На врезке изображена структура контактной волны

На рисунках 4, 5 представлены профили давления и плотности, полученные с применением различных функций-ограничителей, предназначенных для подавления нефизических осцилляций [11]:

L^b)=2

(sign a + sign b)min( | a | , | b | ) ,

L (a, b)

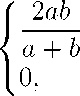
при ab > 0, при ab <  0,

L (a, b)

^{( a} 2 + C ^)b + ^{( b} 2 + C ^)a a² + b ² + 2Z

где a и b — векторы наклонов распределения консервативной величины q внутри ячейки, Z — малая константа. Все перечисленные ограничители удовлетворяют условию невозрастания вариации численного решения (TVD-принцип). Для приближенного решения задачи Римана использовался метод Лакса — Фридрихса . Функция-ограничитель minmod (15), предложенная Роу [9], позволяет получить профиль наиболее приближенный к монотонному, при этом масштабы численной размазки получаются более существенными. Функция-ограничитель (16), предложенная ван Лиром [7], приводит к появлению характерных численных всплесков на границах разрывов. Функция-ограничитель

(17), предложенная ван Альбада [2], позволяет получить профиль без выраженных всплесков с меньшей численной размазкой, чем в случае ограничителя minmod .

Заключение

Полученные решения свидетельствуют об устойчивости численной схемы cSPH-TVD при моделировании сильных ударных волн. Изучены реализации алгоритма с применением методов приближенного решения задачи Римана и различных ограничителей потоков, сохраняющих TVD-свойство разностной схемы.