Численная схема на основе комбинированного подхода SPH-TVD: проблема моделирования сдвиговых течений

Особые требования к численным алгоритмам возникают при моделировании сдвиговых неустойчивостей, которые возникают при изучении самых различных физических объектов и явлений [5; 6; 9–11]. Наиболее трудными представляются системы, допускающие развитие сверхотражения при наличии большого числа неустойчивых мод с близкими значениями инкрементов [7], а также, когда ширина переходной зоны сопоставима с длиной возмущения [3; 6].

Для численного интегрирования уравнений гидродинамики используют два основных подхода. Первый основан на самых различных сеточных методах [2], в основе которых лежит задание сетки, в узлах которой рассчитываются значения величин. Второй, лагранжевый подход, отличается тем, что все физические величины определяются динамическими частицами, на которые разбивается непрерывная среда [12]. Наиболее эффективным представляется метод Smoothed Particle Hydrodynamics (SPH). Стандартная версия SPH-алгоритма обладает недостатком, связанным с невозможностью описания неустойчивости Кельвина – Гельмгольца. Этот эффект наглядно проявляется даже при моделировании распада произвольного скачка давления в одномерном приближении, когда не удается адекватно рассчитывать контактный разрыв.

В работе [8] был предложен новый численный метод, основанный на совместном использовании SPH- и TVD-алгоритмов (cSPH-TVD). В данной работе обсуждается вопрос о возможно- сти применения cSPH-TVD для моделирования неустойчивых сдвиговых течений на примере укороченных уравнений гидродинамики в рамках модели мелкой воды.

Моделирование неустойчивости Кельвина – Гельмгольца

Будем исходить из простой двумерной модели, определяемой системой уравнений Сен-Венана:

д h д ₍   >. д л \

— + — ( hu, ) +—l hu „ )= 0, д t дх        ду^V y'

дu,     дu,     д u,    д Н

—- + ux—- + uy—- = g —, д t     дx     ду    дх д t

д u y      д u y      д u y      д h

—- + ux —-+ u —- = g—, д t       дx    y ду     ду где h(x, y, t) – толщина слоя жидкости; ux(x, y, t), uy(x, y, t) – компоненты скорости; g – ускорение свободного падения. Будем использовать численный метод интегрирования, подробно описанный в работе [8]. Процедура численного интегрирования системы уравнений (1)–(3) разбита на четыре этапа:

• 1)    В начале расчетного цикла (момент времени t_n ) «жидкие» частицы находятся в центрах эйлеровых ячеек. Используя алгоритм Smooth Particle Hydrodynamics, определяем изменения интегральных значений объемов, импульсов жидких частиц и их положения внутри ячеек.

• 2)    На втором этапе рассчитываем потоки массы и импульса через границы эйлеровых ячеек в момент времени t_{n +1/2} , основываясь на модифицированном TVD-подходе и решении задачи Римана.

• 3)    Производим расчет изменений интегральных параметров жидких частиц, связанных с потоками через границы эйлеровых ячеек.

• 4)    На заключительном этапе помещаем частицы в центры ячеек.

В численной модели в качестве единиц измерения выберем единицы системы СИ (метр, секунда) и считаем g = 9,81 м/с². Размер расчетной области составляет 400 х 400 ячеек, площадь ячейки h ² = 6,25 ( h = 2,5). Линейный размер расчетной области равен L = 1 000. В качестве начальных условий примем:

H о = 1 , u о =^

FrJgH /2, У <  0

, v о = ⁰,

Fr^gH 0 /2, У >  0

где Fr – число Фруда.

Результаты расчетов представлены на рисунках 1 и 2 для значения Fr = 1. Возмущение задавалось в виде

~   ( £ИoSin(2nn /L), I у |< h v = 1 „                            , , ,

, I У <  ^h ’

где ε = 10^–4 – относительная амплитуда начального возмущения; n = 2 – число длин волн в интервале от – L /2 до L /2.

Четко выделяются характерные стадии развития неустойчивости тангенциального разрыва скорости на мелкой воде:

• -    Формирование собственной моды (этап A ), когда происходит перестройка начального возмущения в собственную моду без нарастания амплитуды.

• -    На линейной стадии (этап B ) развития неустойчивости рост возмущений следует экспоненциальному закону. Относительная амплитуда волны нарастает до 1-2 % по закону ^ exp ( t / т ) с t = 109 с для параметров течения, изображенного на рисунке 1.

• -    Далее начинается нелинейная стадия развития неустойчивости (этап C ), когда наступает «насыщение» амплитуды возмущений . Формируются характерные вихревые структуры (см. рис. 2), аналогичные тем, что наблюдаются при развитии неустойчивости тангенциального разрыва в газе [1].

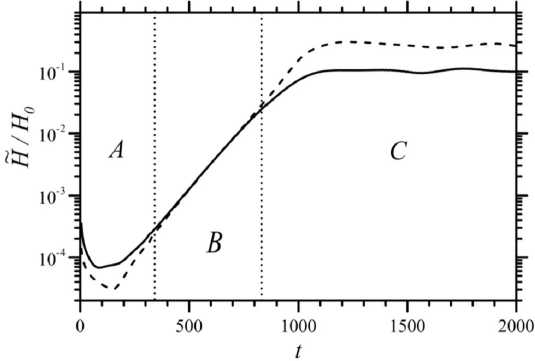
Рис. 1. Зависимость максимальной ( сплошная линия ) и минимальной ( штриховая линия ) амплитуд возмущений глубины ( H ) от времени. Латинскими буквами A , B , C обозначены стадии развития неустойчивости тангенциального разрыва скорости

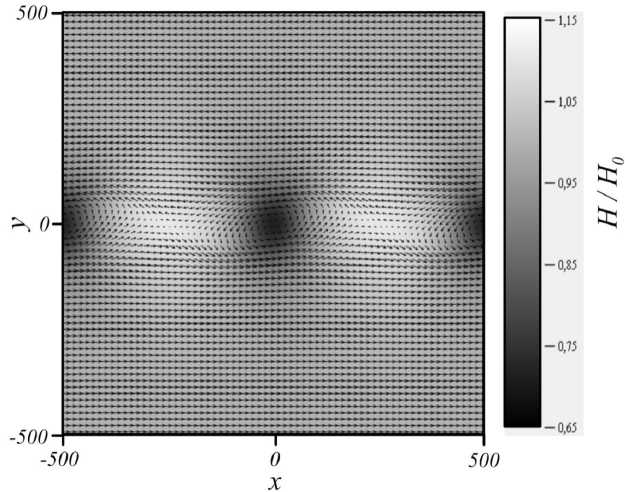
Рис. 2. Нелинейная стадия развития неустойчивости тангенциального разрыва скорости. Представлены распределение глубины Hи поле скоростей v = {u, v} в момент времени t = 1 100

Заключение

Показано, что численный алгоритм cSPH-TVD [8] способен описывать сдвиговые неустойчивости, несмотря на то что на одном из этапов схемы cSPH-TVD используется подход сглаженных частиц SPH. Таким образом, у комбинированного метода cSPH-TVD отсутствует недостаток классического SPH, не позволяющий корректно моделировать тангенциальные и контактные разрывы.

140 А.В. Писарев, С.С. Храпов, А.В. Хоперсков. Численная схема на основе комбинированного подхода