Численно-аналитический метод решения плоской задачи равнонапряженного армирования металлокомпозитных пластин при установившейся ползучести

При проектировании металлокомпозитных пластин целесообразно осуществлять их оптимизацию. Одним из прочностных критериев рационального армирования тонкостенных конструкций является требование равнонапряженности силовых элементов — волокон (проволок) — вдоль их траекторий, так как при этом несущая способность арматуры используется наиболее полно.

При длительной эксплуатации изделия в случае статического термосилового нагружения подавляющую часть времени металлокомпозитная конструкция работает в условиях установившейся ползучести [1], поэтому актуальной является проблема равнонапряженного армирования (РА) тонкостенных конструкций, работающих в условиях установившейся ползучести всех составляющих композицию материалов.

Постановка задачи РА металлокомпозитных пластин, нагруженных в своей плоскости и усиленных волокнами постоянного поперечного сечения, находящихся в условиях установившейся ползучести, и математический анализ соответствующей системы разрешающих уравнений приведены в работе [2], где показано, что получающаяся система квазилинейных уравнений смешанно-составного типа и

соответствующие ей нелинейные граничные условия не позволяют надеяться на построение широкого круга аналитических решений и требуют разработки обоснованных численных процедур решения. В то же время отмеченные в [2] особенности разрешающей системы уравнений не допускают простой перенос известных методов численного интегрирования квазилинейных систем уравнений [3] на решение рассматриваемой задачи.

Настоящая работа посвящается разработке численно-аналитического метода интегрирования плоской задачи РА металлокомпозитных пластин, работающих в условиях установившейся ползучести.

2.    Система разрешающих уравнений и граничные условия

Предполагается, что в равномерно нагретую пластину постоянной толщины внедрено два семейства армирующих проволок постоянного поперечного сечения. С практической точки зрения это условие не является обременительным, так как в композитных пластинах несущие элементы — арматура — должны воспринимать соизмеримые напряжения на площадках, различно ориентированных по двум направлениям. При решении столь сложных обратных задач как РА тонкостенных конструкций целесообразно ориентироваться на достаточно простую структурную модель армированного слоя [4, 5], позволяющую в дальнейшем эффективно проводить анализ возникающих краевых задач и удовлетворительно согласующуюся с известными экспериментальными данными [6]. В рамках этой модели замкнутая система разрешающих уравнений, содержащая в качестве неизвестных функций скорости перемещений при установившейся ползучести v 1 , v 2 и параметры РА го _к , v _к , включает [2]:

уравнения равновесия

• ^{( - 1)} i Е ° к ^го к¹к, ^d s ( v k , V k ) + A i ( v , ^ю ) = ^- Xi ( x , ^ю ) ( i = I,^2, j = ^{3 -} i , ^к = I,² ) , (1) k

условия постоянства поперечных сечений волокон

• ds (vк, юк ) + roк5 N (vк, Vк ) = 0   (к = 1,2),                                           (2)

условия равнонапряженности арматуры

• ^d s ( V к , v i ) cos V к ^{+ d} s ( V к , v 2 ) sin V к = 5 к = / к ( ° к ) = const, ° к = const ( ^к = 1, ² ) , ⁽³⁾

где

A ( V , to ) = 2 [ ag о ( H ) ( 2 v , i + v j j ) ] , i + [ ag о ( H ) ( v. j + j ) ] , j ( ^j = 3 ^- i ) ,

Xi (x, to) = Xi0 (x)a + ^X(к) (x)гок (i = 1,2), a = 1 -Q, Q = ^roк,

• ^lk 1 = cos V к ,      ¹ к 2 = sin V к ,                                                ^к

• ^d S ( v к , i ) = ( i )д cos V к ⁺ ( i ) ,₂ sin V к ,                                                           (4)

• d N (V к, i ) = d S (V к + П/2, i ) = -(i )д sin V к + ( i ),2 cos V к,

v = { V 1 , v 2 } , x = { X 1 , x 2 } , to = { ro 1 , ro ₂ } ,

• ^H = ² V ^v 21 ⁺ v 1,1 v 2,2 ⁺ v 2,2 ^{+ 0,25} ( ^v 1,2 ⁺ v 2,1 ) ²

(суммирование производится по указанному индексу от 1 до 2; нижний индекс после запятой означает частное дифференцирование по соответствующей переменной x_i ; нижние индексы « S » и « N » символизируют продольные ( S ) и поперечные ( N ) направления, в частности, 5 _s ( у k , •) — оператор дифференцирования, по направлению, задаваемому углом у _k , 5 N ( у _k , •) — оператор дифференцирования по направлению, ортогональному к направлению, задаваемому углом у _k ; знак « • » символизирует произвольную функцию, на которую действует соответствующий дифференциальный оператор).

Пусть область G , занимаемая конструкцией в плане, ограничена контуром Г , тогда на одной части этого контура — Г _p , могут быть заданы статические граничные условия [2]

Е ° к ю k cos² ( у k -р ) + D n ( v , ш , ) = P n , k

E ° k ю k sin² ( у k -P ) + D т ( v , « , ) = ² P т ,     ( x i , x 2 ) ^{c Г} p ,

k где

D n ( v , to ) = ² ag 0 ( ^H ) [ ^v i1 ( 1 + n 1 ² ) + v 2,2 ( 1 + n 22 ) ⁺ ( ^V 1,2 ⁺ v 2,1 ) n 1 n 2 D т ( v , « ) = 2 ag о ( H ) [ ² ( V 2,2 - v _u ) n i n 2 ⁺ ( v i,2 ⁺ v 2,1 ) ( ⁿ 2 - n 22 ) ] , n₁ = cos P , n ₂ = sin в ,

а на другой части — Г v , кинематические граничные условия

• V , (^Г V ) = v i (^Г V )    ( i = 1.2 ) .

Кроме того, на части Г_{ю k} контура Г , на которой волокна k -го семейства «входят» в пластину, необходимо задать краевые условия для интенсивностей армирования [2]:

ю k ( Г . k ) = ю о k    ( k = 1,2 ) .                                                            (8)

Решение краевой задачи РА (1)–(3), (5), (7), (8) также должно удовлетворять физическим ограничениям [2]:

0 <ю _k ( k = 1,2 ) ,   0 „ <  1.                                            (9)

В уравнениях и соотношениях (1)–(9) используются обозначения: Xi , vi — компоненты векторов приведенных объемных (массовых) нагрузок и скорости установившейся ползучести точек пластины по направлениям x, (I = 1,2) прямоугольной декартовой системы координат; Xi0 , Xi(k) — компоненты удельных объемных (массовых) нагрузок, действующих на связующее и арматуру k-го семейства; оk, ^k — напряжение и скорость деформации ползучести в k-м семействе арматуры, связанные известной зависимостью Ekk = fk (стk) ; g0 (H) — заданная функция, являющаяся коэффициентом пропорциональности между интенсивностью касательных напряжений T и интенсивностью скоростей деформаций H в связующем: T = g0 (H) H ; tok , уk — интенсивность и угол армирования волокнами к-го семейства (отсчитываемый от направления xr); to, — предельно допустимая удельная суммарная плотность армирования (на практике to, ~ 0,7); pn, pт — нормальные и касательные контурные напряжения соответственно; vi0 — заданные компоненты скорости перемещения точек контура Гv; в — угол, задающий направление внешней нормали к контуру Г; to0k — заданные на контуре rtok краевые значения функций tok .

В случае степенного закона E = B ст m , связывающего скорость деформации ползучести E и напряжение ст в материале каждой компоненты композиции, имеют место зависимости [1]:

g 0 ( H ) = b , H • • ^{- 1}, b 0 = B o' , B 0 = .3 B 0 ,

Цо = Vm0, fk (CTk ) = Bkстm (k = 1,2) ,

где B ₀ , m ₀ , B_k , m_k — известные характеристики установившейся ползучести материалов связующего и арматуры k -го семейства.

В работе [2] показано, что система разрешающих уравнений (1)–(3) представляет собой систему квазилинейных уравнений смешанно-составного типа [7], причем траектории армирования, определяемые углами у _k , являются ее действительными характеристиками. Структура уравнений (1)–(3) и граничных условий (5) (с учетом соотношений (4), (6)) показывает, что задачи определения параметров РА у _k , to _k и поля скоростей установившейся ползучести v ₁ , v ₂ связаны друг с другом и решать их необходимо совместно. Последнее обстоятельство существенно усложняет разработку методов решения нелинейной краевой задачи РА (1)–(3), (5), (7), (8).

З а м е ч а н и е. По известным из решения краевой задачи (1)–(8) скоростям перемещений v_i с помощью формул (1.2)–(1.4) из работы [2] можно вычислить напряженное состояние во всех компонентах и в композиции пластины в целом в условиях установившейся ползучести. Если, помимо этого, известно и начальное напряженное состояние в конструкции ст у (оно определяется, например, методами, изложенными в книге [4], в предположении, что структура армирования ( у _k , to _k ) уже найдена из решения задачи (1)–(8)), то решение задачи о неустановившейся ползучести на первой ее стадии можно получить приближенно, используя методику, предложенную в работе [1]. Для этого текущие осредненные напряжения в пластине представляются в виде:

стj=(r-т(t))сту + т(t)сту (i, j = 1,2) ,

где сту — напряжения в условиях установившейся ползучести (см. формулы (1.2)-(1.4) в статье [2]); т(t) — монотонная функция времени t, возрастающая от значения т = 0 в начальный момент времени t = 0 до т = 1 при t ^ да. Функция т(t) определяется, исходя из экстремальных принципов теории ползучести (см. § 34 работы [1]). В случае изотропных пластин реализация такого подхода не вызывает особых трудностей (так как при этом почти дословно повторяются все рассуждения § 34 [1]), а в случае сложно армированных пластин (который имеет место в рамках рассматриваемой проблемы РА) требуется проведение дополнительного, более тщательного, исследования, выходящего за рамки настоящей работы. Знание функции т(t) позволит оценить момент времени t = t,, при превышении которого (т(t,) « 1) ползучесть во всех компонентах композиции может считаться установившейся. Так как теория ползучести сложно армированных металлокомпозитных конструкций на сегодняшний день находится в зачаточном состоянии [5], то предложенный выше подход является, по-видимому, наиболее удобным с практической точки зрения для оценки условий возникновения установившейся ползучести в металлокомпозитных изделиях.

3.    Метод решения

В настоящее время теория систем квазилинейных уравнений смешанно-составного типа разработана недостаточно полно [7] и не дает возможности в общем случае аналитически исследовать свойства решений замкнутой системы уравнений, математически описывающей проблему РА, поэтому целесообразно воспользоваться какими-либо упрощениями этой системы и соответствующих ей граничных условий.

Важная особенность системы разрешающих уравнений задачи РА (1)–(3) заключается в том, что при выборе определенных материалов, составляющих композицию, слагаемые A_t ( v , го ) в выражении (1) и D n ( v , го , ) , D _т ( v , го , ) в выражениях (5) малы по сравнению с первыми слагаемыми, стоящими в левых частях этих равенств. Действительно, первые слагаемые в (1) и (5) пропорциональны напряжениям в арматуре о k , а значения A i ( v , го ) , D n ( v , го , ) , D _т( v , го , ) , согласно выражениям (4), (6), определяются напряжениями в связующем [2], которые могут быть пренебрежимо малыми по сравнению с о k . Так в случае изготовления металлокомпозитной пластины путем внедрения в медное связующее (Cu) армирующей стальной проволоки (У8А) характеристики материалов компонент композиции (см. выражения (10)) при температуре 0« 200 ° C имеют значения [8,9] (размерность характеристик B i — 1/ [ ( МПа ) m i ч ] , i = 0,1):

Cu: m ₀ = 2,16, B ₀ = 5,63 ■ 10 ^{- 9}, У8А: m 1 = 24,98, B 1 = 1,054 ■ 10 ^{- 84}.

Оценить уровень напряженного состояния в связующем и арматуре позволяет условие для предельно допустимой скорости деформации ползучести 5 _max , которая регламентирована для целого ряда несущих элементов (диски турбин и др.) [10]:

15 k l <%_ = 10 ^{- 9}- 10 - 71 ч      ( к = 0,1,2 ) -

При этом напряжения о k = b k 5 ^pk ( b k = B k ⁴k , p _k = 1/ m_k , к = 0,1,2) в материалах компонент композиции с учетом (10)–(12) соотносятся следующим образом:

I о0/о k| < 4,5 ■ 10-4...3,1 ■ 10-3    (к = 1,2), то есть напряжения в связующем а0 пренебрежимо малы по сравнению с напряжениями в арматуре ak .

З а м е ч а н и е. Подобные оценки малости а ₀ по сравнению с a k ( k = 1, 2) можно получить и в случаях использования в качестве арматуры вольфрамовых проволок [11], а в качестве связующего — алюминиевых сплавов [12] и др. Кроме того, при соответствующем обезразмеривании соотношений (1) и (5) в них может быть выделен малый параметр (например, £ = В 1 /В ₀ , см. характеристики материалов (11)), стоящий сомножителем при A i ( v , го ) , D n ( v , го , ) , D _т( v , го , ) . Однако этот вопрос здесь не рассматривается по причине ограниченного объема статьи.

В силу показанной малости слагаемых A i ( v , го ) , D n ( v , го , ) , D _т( v , го , ) в соотношениях (1), (5) здесь для решения сформулированной задачи РА используется следующий метод простой итерации. Пусть ^), » ks ) , ^{v (} s ) — s "^е приближения неизвестных функций ( i = 1, 2, к = 1, 2 ), тогда ( s + 1)-е приближения получаются путем интегрирования преобразованных уравнений (1)-(3):

(-1) Zaк»r)lj)dS (vkr), Vkr)) = -Xi (x, го(r)) - A (v(s), го(s))    (j = 3 - i, i = 1, 2), k                                                                                  (13)

ds (vkr), <)) + <)dN (vkr), vkr)) = 0   (k = 1, 2), ds (<), v(r))cos vkr) +dS (<), v2r))sin vkr) = ^k = fk (ak) = const, (k = 1,2), (xv x2 )e G при граничных и краевых условиях

Z ^a k » kr ) ^cos 2 ( v kr ) -P ) = P n ^- D n ( v ⁽ s ) , ^го ( s ) ) , k

Z ^a k » kr ) sin² ( v kr ) ^- P ) = ² P т ^- D т ( v ⁽ s ) , ^го ( s ) ) , ( ^X 1 , x 2 ) ^ ^r p , k

v ( r ) ( Г v ) = v ( r v ) , i = 1,2;

» kr ) ( Г » k ) = » 0 k       ( k = 1,2; r = s + 1 ) .

Для начала итерационного процесса нулевое приближение выбирается в виде:

у№ = 0     ( i = 1,2 ) .

Здесь v ⁽ s ) , го ⁽ s ) — векторные функции, подобные v , го (см. выражения (4)).

Для каждого r > 1 система (13), (14) распадается на две подсистемы: первая из них — (13), состоит из четырех квазилинейных уравнений и замкнута относительно приближений параметров РА ^kr), mkr), а вторая — (14), включает два уравнения и при ^kr), известных из (13), замкнута относительно приближений скоростей vkr) (k = 1, 2). Аналогичным образом распадаются граничные и краевые условия (15)-(17): условия (15), (17) состоят из четырех равенств и замкнуты относительно контурных значений функций ykr), tok), а кинематические условия (16) определяют на Гv контурные значения двух функций vkr) (k = 1, 2).

Таким образом, итерационный процесс (13)–(18) позволяет расщепить связанную задачу определения параметров РА и поля скоростей установившейся ползучести на отдельные подзадачи, которые затем интегрируются последовательно на каждой итерации.

Следует более подробно проанализировать уравнения итерационного процесса (13)–(18).

Правые части в двух первых уравнениях (13) могут трактоваться как возмущенные объемные (массовые) нагрузки, при этом система (13) формально совпадает с подробно исследованной в работе [2] системой (3.4), (3.5) и обладает следующими основными свойствами. Согласно работе [2], эта система квазилинейных уравнений с частными производными первого порядка имеет две двукратные действительные характеристики, определяемые углами ^ kr ) ( k = 1, 2 ), но не подпадает ни под один тип существующей на сегодняшний день классификации систем уравнений с частными производными [13]. Система (13) обладает свойствами, присущими как гиперболическим (ее нельзя считать гиперболической, так как она не приводится к характеристической форме [2, 14]), так и параболическим (ее нельзя считать параболической, так как в общем случае в силу неравенства гу ^r ) * у ⁽ ₂ ^r ) характеристики разных семейств различны) системам уравнений. Однако при отсутствии объемных нагрузок ( Х₄ = 0 , i = 1,2) на первой итерации ( r = 1) вследствие выбора начального приближения в виде (18) система (13) распадается на две замкнутые (для каждого k ) подсистемы параболического типа (см. формулу (3.14) в работе [2]). С другой стороны, характеристики системы (13) являются линиями слабых разрывов [2, 14], поэтому, например, решение задачи Коши для неё может быть получено (об этом свидетельствуют многочисленные расчеты, проведенные автором) лишь в области определенности решения, что характерно для решений задачи Коши в случае систем гиперболических уравнений [14].

Так как углы у _k задают траектории РА, а ^ kr ) — r -е приближения к у _k , то и характеристики системы (13) могут трактоваться как r -е приближения к траекториям армирования. Если итерационный процесс сходится, то характеристики системы (13) совпадают в пределе с траекториями РА, которые, в свою очередь, являются характеристиками системы разрешающих уравнений (1)–(3) [2].

Для квазилинейных систем уравнений с действительными характеристиками наиболее естественно и просто ставится задача Коши, поэтому для системы (13) также рассматривается постановка задачи Коши. Поскольку эта система удовлетворяет условиям теоремы Коши–Ковалевской [13], то при аналитических входных данных решение задачи Коши для нее существует и единственно. Для более широких классов входных данных теоремы существования решения системы (13) автору не известны.

Чтобы показать, что статические граничные условия (15) совместно с краевыми условиями (17) задают краевые условия для функций y kr ) , считается, что арматура обоих семейств «входит» в пластину на той части контура, где заданы статические граничные условия: Г _p = Г _{ш k} ( k = 1,2 ) . Тогда система трансцендентных уравнений (15), в силу выполнения краевых условий (17) замкнутая относительно y kr ) ( Г _p ) ( k = 1,2), приводится путем тригонометрических преобразований к виду:

cos ( 2 ф 2 — v ) = ( b 2

+ C —^1 ®01 + ^2®02 )/(2^2^02 ^ + C ) , tg2Ф1 = (b — ^2™02 sin 2^2 )/(C — °2®02 cos 2Ф2 ) ,

V ir ) ( Г p ) = ф _k +P ( к = 1,2),   cos v = c/bb ² + c ²,   sin v = b/bb ² + c ²,

^b = ² P T ^— D t ( v ^{( 5} ) , o ' ⁵ ) ) ,    ^C = ² P n ^— ЭД1 ^— ° 2 ^Ю 02 ,

^P n = P n ^{— D} n ( ^{V 5} ) , ^ ⁵ ) ) ,    r = ^{5 +} 1.

Из граничных условий известно, что функция в, имеющаяся в выражениях (19), задает направление внешней нормали к контуру Г, поэтому для вхождения волокон в область G именно на части контура Гp необходимо решение системы (19) разыскивать на открытом интервале фк е (п/2, 3п/2) . На этом интервале, в зависимости от значений и и правой части, первое уравнение (19) может иметь до двух различных корней, второе же уравнение, при известном ф2, имеет только один корень. Следовательно, система (19) может иметь до двух различных наборов решений относительно vkr) (Гp).

Таким образом, статические граничные условия и краевые условия для интенсивностей армирования задают два набора альтернативных краевых условий системы (13), поэтому в классе аналитических входных данных соответствующая задача Коши (при использовании по отдельности каждого набора краевых условий) может быть поставлена корректно на контуре Г p = Г_{т к} ( к = 1, 2 ) .

При отсутствии распределенных объемных нагрузок ( X_t = 0 , г = 1, 2) задача Коши (13), (17), (19) на первой итерации ( r = 1) интегрируется аналитически (см. формулы (3.14)–(3.24) в работе [2]). При этом из уравнений (13) с учетом выражения (18) и

V ⁽ ₂ r ) ) * 0 в общем случае следует:

неравенства sin

^д 5 ( v kr ) , V kr ) ) = ⁰      ( ^к = 1, ² ) ,

то есть характеристики системы (13) (а также и траектории РА в первом приближении) являются прямыми линиями, определяемыми контурными значениями углов у® ( Г p ) , известными из выражений (19).

Если после интегрирования задачи Коши (13), (17), (19) ее область определенности покрывает всю область G , занимаемую конструкцией в плане, то в каждой точке ( x 1 , x ₂ ) е G известны функции v kr ) , to kr ) . При этом подсистема (14) является линейной гиперболической системой уравнений с частными производными первого порядка относительно приближений скоростей ползучести v_i ^{( r )}, причем характеристики этой системы определяются углами v kr ) и совпадают с характеристиками системы (13). В качестве краевых условий для подсистемы (14) выступают кинематические граничные условия (16), заданные на части контура Г v , где по предположению волокна «выходят» из пластины.

Так как область определенности решения задачи Коши (13), (17), (19) покрывает всю область G и характеристики подсистем (13), (14) совпадают, то после интегрирования задачи Коши (14), (16) в каждой точке ( x 1 , x ₂ ) е G становятся известными функции v ( r ) ( i = 1, 2 ) .

При отсутствии распределенных объемных нагрузок ( X i = 0) на первой итерации ( r = 1) может быть построено аналитическое решение задачи Коши (14), (16). Действительно, выше отмечалось, что при X i = 0 ( i = 1, 2) характеристики системы (13), а значит, и системы (14), на первой итерации прямолинейны, то есть выполняются равенства (20). Поэтому система (14) может быть записана в форме инвариантов Римана [14] с нулевыми правыми частями, после чего легко строится решение задачи Коши (14), (16):

v P) cos v k '’ + v 21) Sin v k '’ - ( x cos v k '’ + x 2 sin v k '’ ) ^ k = v ⁰ ( ? ) cos v^ ( ? ) +

+v0 (?) sin v^ (?) - (П1 (?)cos v® (?) + П2 (?)sin v^ (?))^k (k = 1, 2),

где £ _k = f_k ( o _k ) = const, о _k = const; v^ ( ? ) — значения функций y^ на контуре Г _v , известные из решения задачи Коши (13), (17), (19); n _k ( ?) — функции, задающие точки контура Г _v : x_k = n _k ( ? ) ( k = 1, 2 ) ; ? — естественный параметр вдоль контура (так как характеристики системы (14) при X i = 0 на первой итерации прямолинейны, то в уравнениях (21) имеют место равенства v^ ( x 1 , x ₂ ) = v^ ( ? ) )•

Таким образом, на каждой итерации решение задачи РА сводится к последовательному интегрированию задачи Коши (13), (17), (19) и задачи Коши (14), (16), краевые условия которых задаются на разных частях контура пластины.

Для проверки сходимости итерационного процесса r -е приближения неизвестных функций подставляются в систему разрешающих уравнений и соответствующие ей граничные и краевые условия (см. раздел 2), затем контролируются нормы возникающих при этом невязок. Следует отметить, что невязки появляются лишь в уравнениях равновесия (1) и статических граничных условиях (5) и имеют вид:

5 ( ^r ) = A i ( v ^{( r} ) , co ^r ) , 0 ^{( r} ) ) - A i ( v ^{( 5} ) , w ^{( 5} ) , 0 ^{( 5} ) ) , ( x 1 , x ₂ ) e G ( i = 1,2 ) ,

5 П ^Г ) = D n ( v ⁽ r ) , w r ) , 0 ⁽ r ) ) - D n ( v ^{( 5} ) , w ⁵ ) , 0 ^{( 5} ) ) , (22)

5 T r ) = D _T ( v ⁽ r ) , w ' r ) , 0 ⁽ r ) ) - D _T ( v ^{( 5} ) , w ' ⁵ ) , 0 ^{( 5} ) ) , ( X 1 , x 2 ) ef p , r = 5 + 1.

Эти равенства показывают, что в итерационном процессе определение невязок не требует дополнительных вычислительных затрат, так как все выражения, входящие в (22), вычисляются в силу необходимости при построении решения на ( r + 1 )-й итерации. Автор считает, что на настоящий момент времени контроль норм невязок (22) является наиболее удобным практическим критерием проверки сходимости процесса (13)–(18).

Так как равенства (17), (19) допускают наличие на контуре Гp до двух альтернативных наборов краевых условий (выбор того или иного набора этих условий определяется или волей проектировщика, или какими-либо дополнительными соображениями) для системы (13), удовлетворяющей условиям теоремы Коши– Ковалевской [13], а также в силу единственности решения задачи Коши (14), (16) [14], возможно построение при помощи итерационного метода (13)–(18) до двух различных решений исходной задачи РА, если, конечно, они существуют. Эти решения управляются варьированием контурных функций ш0k в краевых условиях (17) (так как выбор того или иного решения всецело зависит от проектировщика, то в процессе решения задачи РА при использовании разработанного итерационного метода не может произойти «несанкционированный» переход от одного решения к другому, например, за счет погрешности численных схем и т.п.). Такое многообразие альтернативных проектов РА выгодно с практической точки зрения, так как оно позволяет выбрать проекты, обладающие теми или иными эксплуатационными свойствами, а также наиболее удобные с точки зрения технологической реализации. Кроме того, за счет варьирования функций ю0к в краевых условиях (17) и уровня напряжений в арматуре ок можно добиться выполнения физических ограничений (9), если при некоторых значениях «0к, оk ( к = 1, 2 ) они нарушаются.

Так как системы уравнений (13), (14) имеют только действительные характеристики, то задача Коши для них интегрируется численно с помощью некоторой адаптации метода характеристик [14]. Однако применительно к итерационному процессу (13)–(18) этот метод обладает существенным недостатком. Важная особенность итерационного процесса заключается в том, что для определения приближений v_i ^{( r )} требуется интегрирование системы гиперболических уравнений первого порядка (14), а для продолжения итерационного процесса эти приближения необходимо дважды продифференцировать, о чем свидетельствует структура операторов A ( v , ^ю ) (см. выражения (4), (13)). Следовательно, порядок уравнений, определяющих величины v_i ^{( r )}, меньше порядка их производных, требующихся для построения следующего приближения решения задачи РА.

З а м е ч а н и е. Следует заметить, что в классических задачах механики деформируемого твердого тела ситуация, как правило, противоположна — порядок уравнений, описывающих неизвестные функции, больше порядка их производных, требующихся затем для каких-либо целей. Эта особенность итерационного процесса (13)–(18) требует при его численной реализации высокой точности интегрирования систем (13), (14). Метод же характеристик обычно имеет точность второго порядка [14], поэтому дальнейшее численное определение производных от функций v_i ^{( r )} может привести либо к полной потере точности, либо к быстрому накоплению ошибок с увеличением количества итераций, что затруднит проверку сходимости итерационного процесса (см. формулы (22)).

В силу указанных обстоятельств при численной реализации итерационного процесса (13)–(18) является целесообразным использование высокоточных устойчивых методов, основанных, например, на обобщении идей методов Рунге–Кутты [15]. По причине ограниченного объема статьи эти вопросы здесь не обсуждаются; необходимо лишь отметить, что при проведении расчетов используются обобщенные методы Рунге–Кутты четвертого порядка, вполне обеспечивающие требуемую точность решения, а тестирование результатов численного интегрирования проводится путем сравнения с точными аналитическими решениями (см. формулы (20), (21) и (3.14)–(3.19) [2]), при этом точность численного расчета имеет порядок 10 - 8 ... 10 - 6 .

4.    Обсуждение результатов расчетов

В качестве примера рассматривается расчет РА-структур при установившейся ползучести металлокомпозитной двусвязной пластины, ограниченной контурами, уравнения которых заданы в полярной системе координат ( r , ф ) (размерность r — метры):

г p = г . , = Г „ 2 : r ( ф ) = 0,4 + 0,04cos ( 3 ф ) ,

Г v : r ₂ ( ф ) = 1 + 0,08cos ( 4 ф ) (0 <ф< 2 п ).

Внешний контур Г v пластины жестко закреплен ( v 10 ( ф ) = v 0 ( ф ) = 0), а на внутреннем контуре Г p заданы равномерно распределенные контурные нагрузки p n или p _т . Распределенные объемные нагрузки отсутствуют ( Х₄ = 0, i = 1,2). Пластина изготовлена из меди и армирована двумя семействами стальной проволоки У8А (механические характеристики установившейся ползучести составляющих композицию материалов определяются соотношениями (10), (11)).

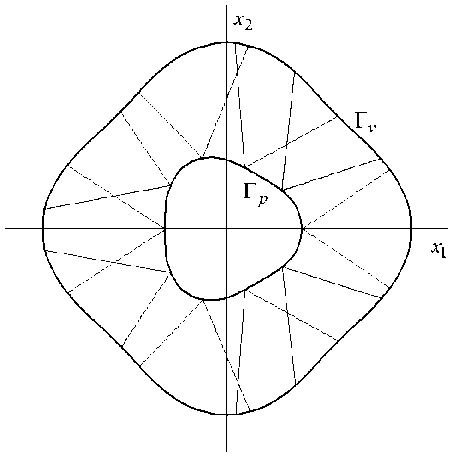
На рисунке 1 изображены РА-структуры, полученные в случае нагружения внутреннего контура давлением p n = - 500 МПа ( p _т = 0) при задании уровня напряжений в арматуре о 1 = о ₂ =- 1 ГПа. Рисунок 1, а соответствует случаю, когда плотности армирования на внутреннем контуре имеют значения (см. выражения (8), (17))

“.(Г p ) = “2 (Г p ) = “„ (ф) = «02 (ф) = 0,35, Г p = Г„, =Г„2, (23)

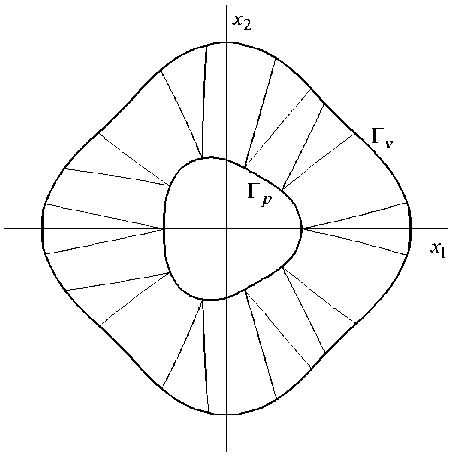
а структура, изображенная на рисунке 1, б , соответствует значениям

“1 (Гp) = “2 (Гp) = - (ф) = “02 (ф) = 0,26, Гp = Г. = Г.2.

Сравнение проектов, приведенных на рисунке 1, а и б , позволяет проследить за качественным изменением РА-структур при варьировании функций “ ₀ k в краевых условиях (8), (17). Эти проекты отличаются не только качественно, но и количественно. Так во втором проекте (Рис. 1, б ) общий расход арматуры на 18,4% меньше, чем в первом (Рис. 1, а ). Кроме того, во втором проекте максимальное значение интенсивности напряжений в связующем и максимальная по модулю скорость ползучести точек внутреннего контура соответственно на 11,6% и 10,5% меньше, чем в первом случае. Следовательно, структура, изображенная на рисунке 1, б , лучше структуры на рисунке 1, а как по расходу арматуры, так и с точки зрения податливости и уровня напряженного состояния в связующем (приведенный пример показывает, что не всегда увеличение объемного содержания арматуры в композитной конструкции приводит к улучшению ее свойств). Структуры армирования, соответствующие вторым возможным решениям рассматриваемой задачи РА, совпадают с уже изображенными на рисунке 1 с той лишь разницей, что в них траектории разных семейств меняются местами (с технологической точки зрения это одни и те же проекты).

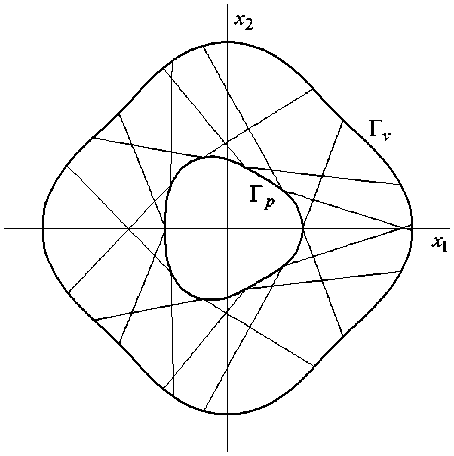
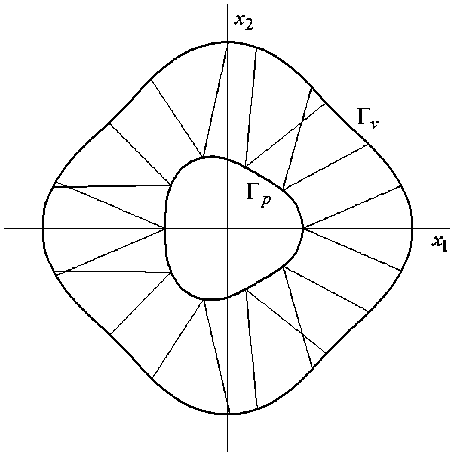
На рисунке 2 изображены две альтернативные РА-структуры, полученные в случае нагружения внутреннего контура касательной нагрузкой p _т =- 250 МПа ( p_n = 0), при задании уровня напряжений в арматуре о 1 = -о ₂ = 1 ГПа и плотностей армирования на внутреннем контуре в виде (23). При этом существуют оба решения задачи РА, и, как видно из рисунка 2, структуры армирования в них существенно различаются. Наряду со структурой различие наблюдается и в напряженном состоянии, возникающем в связующем. Так в проекте, изображенном на рисунке 2, б , максимум интенсивности напряжений в связующем на 55,1% меньше той же величины в проекте, представленном на рисунке 2, а . Помимо этого, в указанных проектах различаются и поля скоростей установившейся ползучести и общий расход арматуры, который в случае, изображенном на рисунке 2, б , на 90,3% больше, чем в РА-структуре, приведенной на рисунке 2, а ; максимальная же по модулю скорость ползучести в проекте 2, б на 84,4% больше, чем в проекте 2, а . Следовательно, целесообразнее использовать РА-структуру, изображенную на рисунке 2, а .

а                                        б

Рис. 1. Структуры равнонапряженного армирования двусвязной пластины, нагруженной на внутреннем контуре давлением

а б

Рис. 2. Два альтернативных проекта равнонапряженного армирования двусвязной пластины, нагруженной на внутреннем контуре касательными нагрузками

Необходимо подчеркнуть, что возможность построения двух альтернативных РА-проектов определяется тем, что задачи РА относятся к разряду обратных задач механики композитов (а точнее, к специфическим коэффициентным задачам), которые, как известно, могут иметь неединственное решение.

У всех приведенных на рисунках структур траектории армирования визуально практически не отличаются от прямых линий. Это вызвано пренебрежимо малым (в силу выражений (11) и |с _к | = 1 ГПа) возмущением правых частей в уравнениях (13), а при X k = 0 ( к = 1,2), как показано ранее (см. формулу (20)), РА-траектории в первом приближении прямолинейны.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 07-08-00152–а).