Численно-экспериментальное исследование влияния технологических несовершенств геометрии силовых стержней на напряженное состояние и оптические характеристики световода типа “Панда”

В настоящее время оптическое волокно считается самой совершенной физической средой для передачи информации, в том числе на значительные расстояния [1-3]. Для изготовления высокоточных датчиков таких как волоконно-оптический гироскоп используется специальный тип волокна, так называемое анизотропное одномодовое волокно [4, 5], например, волокно типа “Панда”. Такое волокно сохраняет состояние поляризации вводимого в него излучения. Эффект достигается за счёт создания в светопроводящей жиле анизотропии распределения полей остаточных напряжений. Это достигается путем введения в заготовку волокна специальных силовых стержней из кварцевого стекла, легированного небольшими добавками примесей, значительно увеличивающих коэффициент линейного температурного расширения

и уменьшающих температуру стеклования [6, 7]. В процессе изготовления волокна после охлаждении от 2000 ° С до температуры окружающей среды в светопроводящей жиле волокна формируется необходимый уровень разности главных механических остаточных напряжений, который в рамках действия фотоупругих эффектов способствует изменению двулучепреломления.

При проектировании конструкции волокна и выбора параметров технологического процесса его изготовления предполагается, что волокно, его заготовка и конструктивные элементы волокна и заготовки имеют идеальные геометрические формы. У волокна типа “Панда” сечения светопроводящей жилы и силовых стержней должны иметь круглую форму, центры светопроводящей жилы и волокна совпадать, а центры силовых элементов находится на одинаковом расстоянии и на одной прямой, проходящей через центр волокна [8-10]. Однако технологический процесс изготовления волокна связан со сложным поведением материала в широком температурном диапазоне, при котором неоднородно легированный материал из вязкотекучего состояния переходит в стеклообразное. В таких условиях, когда остаточное напряженное состояние определяется совокупностью факторов, связанных со свойствами материалов и условиями технологического процесса изготовления, имеющиеся не- совершенства геометрии могут влиять на механические и оптические характеристики волокна. В данной работе исследуется влияние отклонений некоторых геометрических параметров силовых стержней в составе готового волокна от их проектных значений.

ИЗМЕРЕНИЕГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ПОПЕРЕЧНОГО СЕЧЕНИЯ ВОЛОКНА

Геометрические параметры поперечного сечения каждого оптического волокна типа “Панда” фиксировались с помощью измерительной системы PK-2400, всего исследовано 1400 образцов. На рис. 1 представлена схема части кругового сечения волокна с указанием характерных замеряемых геометрических параметров.

Предполагается, что волокно с границей Г, стержни и светопроводящая жила имеют идеальное круговое сечение, а разбросы возможны в величинах диаметров стержней, жилы и в располо- жении их центров по отношению к проектным позициям. Точки 0,5 1,52, C - центры волокна, первого, второго силовых стержней и светопроводящей жилы соответственно; D – диаметр волокна; Di, D2, De – диаметры первого и второго силовых стержней, а также светопроводящей жилы соответственно; L1, L2, Lc - расстояния от центра волокна до центров силовых стержней и жилы; ф1, ф2, фс - углы между отрезками, соединяющими центры силовых стержней, светопроводящей жилы с центром волокна и основной осью (здесь и далее под основной осью понимаем прямую, параллельную отрезку, соединяющему центры силовых стержней, проходящую через центр волокна).

СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

На основе измеренных данных получены статистические зависимости, характеризующие реальное распределение геометрических пара- метров волокна “Панда” и его конструктивных элементов. Полученные значения представлены на графиках в условных безразмерных единицах вычисленных по формуле: Y' = Y/Yep , где Y -анализируемое значение, Yср – среднее арифметическое значений соответствующей геометрической характеристики. При анализе параметров геометрических характеристик силовых стержней порядок стержней (первый или второй стержень) не определяется, поэтому Di – объединённый набор величин D1, D2, Lt - объединённый набор величин L1,L2, а фi - объединённый набор величин ф1,ф2.

В математическом пакете STATISTICA подобраны законы распределения геометрических параметров, рис. 2-7. Из результатов подбора распределения для определенной выборки присваивается тот закон распределения из исследованных, который при найденных значениях его параметров дает минимальные значения статистики Колмогорова-Смирнова и статистики хи- квадрат.

Распределения диаметров волокна, силовых стержней и светопроводящей жилы стремятся к нормальному закону. При этом диаметры волокна D варьируется в небольших диапазонах (<1%), (рис.2), а диаметры силовых стержней D_i (рис.3) и диаметры светопроводящей жилы D_c (рис.4.) варьируются в пределах 10%.

Расстояние от центров силовых стержней до центров волокна L_i изменяется в пределах 10% по нормальному закону распределения (рис. 5).

Расстояние от центра светопроводящей жилы до центра волокна L_c подчиняется логнормальному закону (рис. 6).

На основе обработки экспериментально замеренных значений двулучепреломления световода B , установлено, что данная характеристика коррелирует с такими величинами как диаметры силовых стержней D_i и расстояния от центров стержней до центра волокна L_i в соответствии с формулой вычисления нормированного коэффициента корреляции:

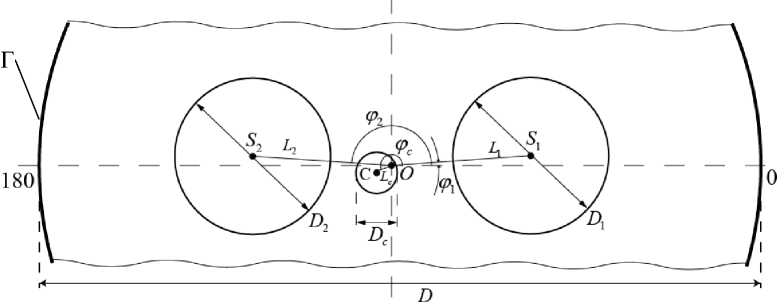
Рис. 1. Схема области поперечного сечения оптического волокна типа “Панда”, содержащей конструктивные элементы

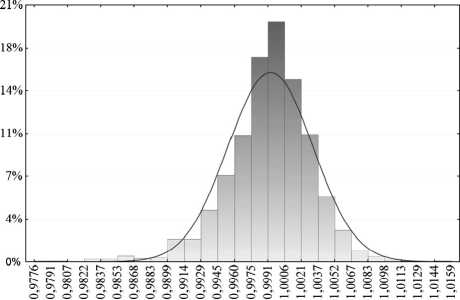
Рис. 2. Гистограмма распределения диаметра волокна D '

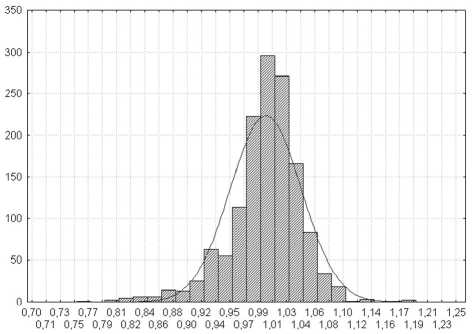
Рис. 3. Гистограмма распределения диаметров силовых стержней D i '

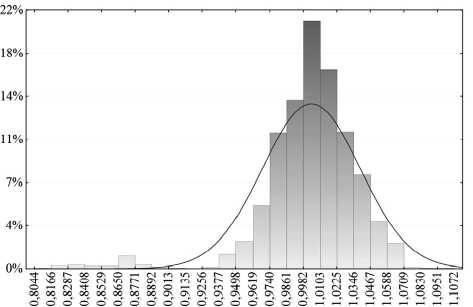
Рис. 4. Гистограмма распределения диаметра светопроводящей жилы D c '

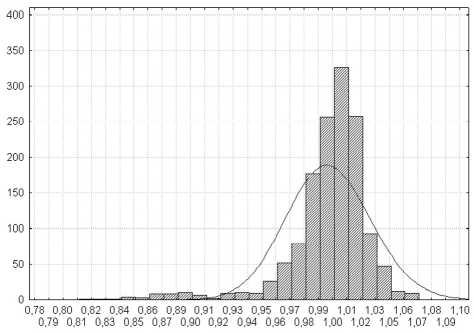
Рис. 5. Гистограмма распределения расстояний от центров силовых стержней до центров волокна L i '

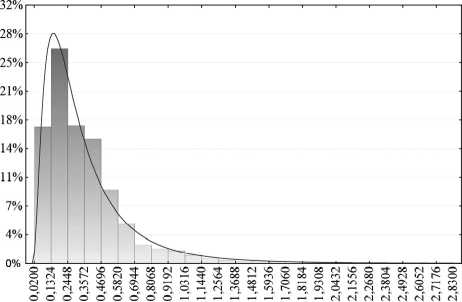
Рис. 6. Гистограмма распределения расстояний от центра светопроводящей жилы до центра волокна L_c

r = M (Rn - M (Rn))M (Rm - M (Rm )) rnm

,

σσ nm

где R n , R m – распределение величин, M – математическое ожидание, o n , o _m - средние квадратичные отклонения для R_n и R_m соответственно.

Двулучепреломление B прямо пропорционально диаметрам силовых стержней ( rBD = 0,56) и обратно пропорционально расстоянию от центров силовых стержней до центра волокна ( rBL = -0,22). По результатам статистического и корреляционного анализа геометрических параметров выделены диапазоны изменения значений величин влияющих на величину двулучепреломления.

ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ

И ДВУЛУЧЕПРЕЛОМЛЕНИЯ

Рассмотрим задачу о нахождении остаточных напряжений, возникающих в результате охлаждения волокна до температуры окружающей среды после вытяжки из заготовки под действием высокой температуры (~ 2100°C ). Процесс связан с переходом материала из вязкоупругого состояния в стеклообразное. В статье [8] показано, что при решении задачи теплопроводности об охлаждении волокна в процессе вытяжки температура на поверхности и в центре волокна отличаются несущественно. Поэтому решение квази-статической краевой задачи (считаем, что процесс зависит от времени, но при этом скорости настолько малы, что силами инерции можно пре- небречь) об изменении полей напряжений ведём с учётом предположения об однородности температуры в поперечном сечении волокна и зависимости от времени, установленной в [8]. Тогда задача о нахождении напряжённо-деформированного состояния волокна соответствует случаю обобщенной плоской деформации и включает уравнения равновесия:

da ( x , y , t ) ₊ T ( ^x , У , t ) = ₀

ex           8y’

T ^{( x} , У , t ) ₊ ^{da (} x , У , t )

d x          d y

= 0,

x , У e S .

геометрические соотношения:

d u ( x , y , t )                    o u ⁽ x , y , t )

Ex (x, У, t) =     -      , Ey ( x, У, t) = —4, ox

.       . du_x ( x , y , t ) S u ⁽ x , y , t )

Yxy(x, У, t) = x '         + dy

x, y G S .

граничные условия:

^ x ⁽ x , y , t ) n x ^{+ T} xy ⁽ x , y , t ) n y = ⁰

^ xy ⁽ x , y , t ) n x ^{+ a (} X , y , t ) n y = ⁰

x , y еГ , физические соотношения:

4_z

CT x ^{( x} , y , t ) = ⁽ B ⁺ 3 G ) ( ^E x ^{( x} , y , t ) ^- S ex ^{( x} , y , t ) ^-

• -    St ( x , y , t ) ) + ( B - 3 G ) ( S y ( x , y , t ) - S ey ( x , y , t ) - St ( x , y , t ) )

2_z

CT y ⁽ x , y , t ) = ⁽ B ^- 3 G ) ( ^S x ⁽ x , y , t ) ^{- S} ex ⁽ x , y , t ) ^-

• ^{-    S} T ⁽ x , y , t ) ) ^{+ (} B ⁺ 3 G ) ( ^S y ⁽ x , y , t ) ^{- S} ey ⁽ x , y , t ) ^-S T ⁽ x , y , t ) ) ,

S             1Bx^(x,y,t) = -(^x - a) t            n

S1

-f (x,y,t) = -(ay -a), x,y e S, t n где t — время, n - внешняя нормаль к Г ,

T

S T ( x , y , t ) = J a ( T ) dT - температурная деформа- T )

ция, SBx (x, y, t), Sey (x, y, t) - компоненты тензора вязких деформаций S в .a = akk / 3 - среднее напряжение, EL - единичный тензор второго ранга. Девиатор тензора вязкой деформации eв(x, у, t) = Sв(x, y, t)- 3 9в(x, y, t)E? , в силу того, что в расплавленном состоянии материал предполагается несжимаемой жидкостью (9b = 0). равен тензору вязких деформаций eB = S;B; 9B = SBk - объемная деформация. В -модуль объемного сжатия; G – модуль сдвига

Вследствие неоднородного легирования силовых стержней коэффициент линейного температурного расширения а и вязкость П являются функциями концентраций легирующих элементов и координат.

U ⁽ ц ^{( x} , у ))

а = а ( ц ( x , y )) . n = П 0⁽ Ц ^{( x} , У )) e R ⁽ x ’ ^у ’ t ) . где U(_p, ( xx , y )) - энергия активации. R - универсальная газовая постоянная. ц ( x , у ) - концентрация легирующих элементов. Известно [6], что влияние небольших степеней легирования кварцевого стекла на упругие характеристики незначительно.

В конечно-элементном пакете ANSYS проводится численный эксперимент по нахождению остаточных напряжений в процессе изготовления кварцевого оптического волокна типа “Панда”, позволяющий задавать реальную форму геометрии волокна и его конструктивных элементов.

В результате вычислительных экспериментов выявлено, что при отклонении формы сечения волокна от проектной величины количественно напряжения изменяются незначительно. Так, например, на рис.7. приведены распределения интенсивностей напряжений при разных отклонениях формы геометрии и разница между максимальными значениями составляет не больше 3%. Меняется качественное распределение напряжений по сечению, в том числе и в области светопроводящей жилы, что влечёт за собой возможность изменения величины двулучепреломления В, которое в данном случае вычисляется по формуле:

» 2 п

B = C(^)J J (ax (r, ^) - ay (r, ^))E(r, ф, V)2 rdrdP Х 0 0

Х

J 2[|E (Г ,ф, V ) 2 ММф)

V 0 0                      J где Г, ф - соответствующие оси цилиндрической системы координат. О x и О’ у - нормальные напряжения в поперечном сечении волокна. С (X ) -фотоупругая постоянная для данной длины волны. |E (r, ф, V ) - распределение интенсивности основной моды по поперечному сечению све-

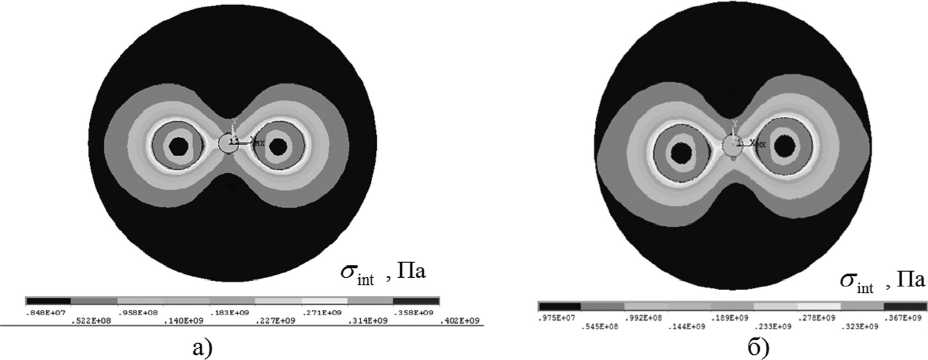
Рис. 7. Интенсивность напряжений σ _int в волокне: а – проектная форма; б – форма с отклонениями

B⋅10-4

B ⋅10-4

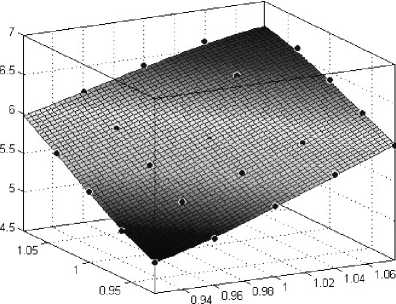
а)

б)

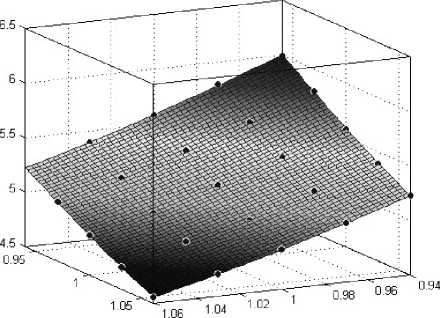
Рис. 8. Зависимость модового двулучепреломления световода B от значений а – диаметров силовых стержней D ₁' и D ₂';

б – расстояний от центров силовых стержней до центра волокна L ₁ и L ₂

товода. В данном исследовании принималось равномерное распределение E ( r , ф, V ) = E ₀ .

Выполнены численные исследования напряженного состояния оптического волокна Panda и определены величины модового двулучепреломления при установленных наиболее вероятных разбросах диаметров силовых стержней D ₁, D ₂ и расстояний от центров стержней до центров волокна L ₁ и L ₂ (рис.8).

Методом наименьших квадратов получены удобные в инженерных целях аппроксимирующие выражения поверхностей полными кубическими полиномами.

B ( D ', D 2 ') = b oo + b io D ' + b oi D 2 ' + b 20 D '² + b„D ' D 2 + ' + b ₀₂ D ₂ '² + b 30 D 1 '3 + b ₂₁ D 1 '² D ₂ ' + b ₁₂ D 1 ' D ₂ '² + b 03 D ₂ '3 b ₀₀ = 0,03249 ; b ₁₀ = - 3022 ; b ₀₁ = - 3022 ; b ₂₀ = 1,178 E + 08 ; b _X1 = 1,405 E + 08 ; b ₀₂ = 1,178 E + 08 ; b ₃₀ = - 1,639 E + 12 ; b ₂₁ = - 2,211 E + 12 ; b ₁₂ = - 2,211 E + 12 ; b ₀₃ = - 1,639 E + 12

B ⁽ L 1 , L 2 ) = ^b 00 ^{+ b} 10 L 1 ^{+ b} 01 L 2 ^{+ b} 20 L 1   ^{+ b} 11 L 1 L 2 ⁺'

+ b 02 L 2 '² + b 30 L 1 '³ + b 21 L 1 '² L 2 ' + b 12 L 1 ' L 2 '² + b 03 L 2 '³

b ₀₀ = 0,03924 ; b ₁₀ = 607,7 ; b ₀₁ = 607,7 ; b ₂₀ = 5,263 E + 07 ; b 11 = 7,931 E + 06 ; b ₀₂ = - 5,263 E + 07 ; b ₃₀ = 1,28 E + 12 ;

b ₂₁ = - 7,839 E + 10 ; b ₁₂ = - 7,839 E + 10 ; b ₀₃ = - 1,28 E + 12

Установленный численно нелинейный характер зависимости отражает установленную ранее экспериментально корреляционную зависимость, состоящую в том, что увеличение диаметра силовых стержней при фиксированном положении их центра приводит к увеличению величины двулучепреломления, а увеличение расстояний от центров силовых стержней до центра волокна L ₁ и L ₂ приводит к уменьшению величины двулучепреломления. При этом разброс величины двулучепреломления при разных реализациях геометрии достигает 30%.

ЗАКЛЮЧЕНИЕ

Таким образом, путем статистической обработки результатов экспериментальных измерений отклонений некоторых геометрических параметров силовых стержней в составе готового волокна от их проектных значений, а также численного исследования влияний этих отклонений на остаточные напряжения в анизотропных оптических волокнах типа “Панда”, установлено существенное изменение двулучепреломления (разброс до 30%) - важной оптической характеристики волокна.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, гранта РФФИ проект № 13-08-96036 р_ура-л_а и 14-08-31530 мол_а.