Численное и экспериментальное моделирование конвективного теплообмена при течении жидкого металла в кольцевой трубе

Трубчатые контуры систем охлаждения, широко используемые в энергетическом оборудовании, часто включают в себя изогнутые участки труб. Наиболее эффективными и компактными теплообменниками являются змеевики. В такой трубе центробежные силы приводят к образованию в текущей жидкости двух вторичных вихрей с осями, параллельными оси трубы. Вихри дополнительно перемешивают жидкость и тем самым интенсифицируют теплоотдачу [1] .

Моделирование процессов гидродинамики и теплообмена осложняется геометрией змеевиков, все поверхности которых криволинейны. Аппроксимирующие расчетные сетки строят обычно в декартовой системе координат, они, как правило, существенно неструктурированные и состоящие из непрямоугольных элементов. Авторами настоящей работы в модельных расчетах потоков в изогнутых трубах предлагается перейти в криволинейную систему координат и в соответствии с ней взять за основу цилиндрические координаты (r,φ,z) [2, 3] , изогнутые по кольцу, с базисным вектором e ^,w , зависящим от (г,ф). В постановку задач для змеевиков добавляется «винтовой» поворот системы координат относительно оси трубы с базисным вектором e ^, _q , зависящим от z. На практике используются змеевики с большим радиусом витков R и малым шагом между ними, так что «винтовым» поворотом можно пренебречь и отыскивать решение в кольцевой области. Но возникает сложность при записи в кольцевой системе координат дифференциальных уравнений, а именно уравнений Навье–Стокса и энергии (удельной энтальпии). Решение этой задачи представлено авторами в работах [4, 5] . За основу взята система уравнений в цилиндрической системе координат (ЦСК) [2, 6] с введением некоторых добавочных слагаемых. Подробный вывод уравнений дается в [5] .

Задачи гидродинамики и теплообмена в изогнутых трубах известны давно и исследовались как экспериментально [6] , так и теоретически [7] . Однако вывод разрешающих уравнений в криволинейных координатах не получил должного распространения. Как правило, производится преобразование систем координат, например, цилиндрической в тороидальную, а эксперименты выполняются в основном в диэлектрических средах (в воздухе, воде, органических жидкостях). Специфика же жидкометаллических (ЖМ) теплоносителей определяется их свойствами (в частности, низким числом Прандтля) и особенностями теплоотдачи. Распределения локальных значений коэффициентов теплоотдачи неравномерны как по длине трубы, так и по периметру сечения и могут значительно отличаться от своих средних величин. Близкая задача — МГД течение жидкого натрия в тороидальном канале, решалась аналитически и исследовалась экспериментально применительно к проблеме МГД динамо [8, 9] . При этом в аналитическом подходе к решению для учета кривизны канала используется метод возмущений с разложением в ряд функций поля течения [8] . Однако эта задача слишком специфическая: тороидальный канал с жидким металлом вращается.

Статья опубликована в открытом доступе по лицензии CC BY 4.0

В настоящей работе предлагается более ясная и точная методика, базирующаяся на общих уравнениях (в обобщенной системе координат) [10, 11] , а экспериментальные данные получены в потоке жидкого металла на основе локальных зондовых измерений. Поскольку авторами накоплен большой опыт работы на уникальных ртутных стендах [12, 13] , существующих и построенных вновь в МЭИ и ОИВТ РАН, объединенных в единый комплекс исследований процессов гидродинамики и теплообмена в трубах и каналах систем охлаждения ядерных и термоядерных реакторов и установок, а также в исследовании МГД динамо и теплообмена при течении ртути, то возникала идея провести натурные эксперименты в изогнутой трубе и на практике проверить работоспособность предложенной расчетной методики. Вместе с тем эти испытания интересны сами по себе, так как ЖМ являются приемлемыми теплоносителями, но еще недостаточно изученными с позиций гидродинамики и теплообмена.

Трудности в обретении экспериментальной информации о ЖМ потоках связаны с высокой температурой плавления почти для всех металлов, кроме ртути. Поэтому имеющиеся в литературе данные измерений получены преимущественно на ртути. Их, используя методы подобия, можно переносить на другие теплоносители, например, на свинец и его сплавы. Свинцовый теплоноситель считается наиболее перспективным теплоносителем в ядерных реакторах нового поколения [14, 15] , однако в среде ЖМ измерение локальной скорости затруднены. Непрозрачность, высокая плотность, электропроводность, существенная неизотермичность среды делают большинство методов измерения скорости, широко распространенных в диэлектрических средах, не применимыми в потоке ЖМ, тогда как в ртути (жидкой при комнатной температуре) широко практикуются зондовые методики. В последних используются микротермопарные датчики, позволяющие находить среднюю локальную скорость корреляционным методом [16] . Этот метод требует оснащения высокоточным скоростным измерительно-вычислительным оборудованием и современным программным обеспечением.

В настоящей работе приводятся результаты серии экспериментов по измерению профилей продольной компоненты скорости V _z . Благодаря конструкции датчика, состоящего из двух термопар, сняты подробные данные о потоке и построены поля осредненной скорости и температуры, а также интенсивности температурных пульсаций в сечении обогреваемой трубы, изогнутой по дуге.

• 2.    Постановка задачи

Решается задача неизотермического течения ртути в трубе, имеющей внутренний диаметр d= 19 мм, толщину стенки 3 мм и длину L = 100d. В горизонтальной плоскости труба изогнута в виде кольца, радиус кривизны которого (по оси вращения трубы) составляет R = 0.5 м, а длина его половины меньше длины трубы (Рис. 1) . Снаружи на трубу действует тепловой поток q w , постоянный как по периметру сечения, таки по длине L q = 80d. Участку обогрева предшествует участок гидродинамической стабилизации протяженностью 20d. Вектор ускорения свободного падения g перпендикулярен плоскости кольца.

Труба встроена в контур стенда РК-3, находящегося в ОИВТ РАН (г. Москва) (Рис. 2) . Стенд обеспечивает стабилизированный поток ртутного теплоносителя в диапазоне чисел Re = 5000 ^ 100000. На трубе смонтирован нагреватель косвенного обогрева в виде нихромовой ленты (сечением 8 x 0.2 мм ² ), плотно намотанной на трубу. Нагреватель обеспечивает тепловой поток q w до 35 кВт/м ² . С торца рабочего участка навстречу потоку вводится зонд рычажного типа [16] с корреляционным микротермопарным датчиком на конце. Зонд изготовлен из трубок и капилляров, телескопически набранных по его длине так, чтобы в поток вносились минимальные возмущения. Двухкоординатный механизм с приводом на шаговых двигателях позволяет перемещать датчик в любую точку в интересующем сечении потока. Две медь-константановые термопары датчика с толщиной спаев 0.1 мм расположены на расстоянии l 12 =2.1 мм друг от друга. Скорость определяется по среднему времени ∆τ,

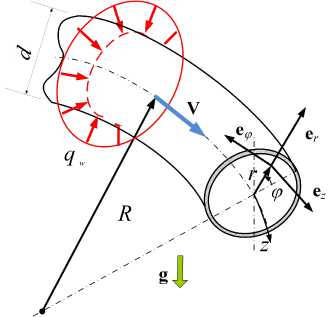
Рис. 1. Схема течения

Рис. 2. Стенд РК-3 с кольцевой трубой

за которое температурное возмущение преодолевает путь между термопарами: V z = 1 12 /Ат . Для этого снимаются осциллограммы с двух термопар с помощью скоростных мультиметров NI PXI-4072 и строится корреляционная функция двух сигналов согласно формуле:

t 0

R xy (т )

lim t 0 →∞

j T 1 (t)T ₂ (t+т )dt.

Период реализации составляет t ₀ = 60 с, а частота опроса — 10 кГц. Время Ат определяется по сдвигу максимума корреляционной функции [16] . Первичная обработка сигналов осуществляется по программе, написанной в среде LabView.

Численное моделирование течения в криволинейной системе координат имеет преимущество перед моделированием в декартовой системе за счет простоты построения сетки — она по-прежнему строится подобно ЦСК, то есть для прямой трубы. Сетка остается структурированной, универсальной для разных радиусов кривизны R трубы, ее можно сгущать вблизи стенки. Координатные поверхности совпадают с границами раздела фаз, что упрощает задание граничных условий.

3. Система уравнений для расчета в кольцевой системе координат

Стационарное течение и теплообмен жидкого металла можно описать системой дифференциальных уравнений, включающей уравнение неразрывности, уравнения движения и энергии в векторном виде:

V = 0,

p( V • V ) V = - V p + V^ V +p f ,

pC p ( V • V )T = VAV T.

Здесь приняты обозначения: ρ — плотность; p — давление; µ — динамический коэффициент вязкости; λ — теплопроводность; C p — теплоемкость среды; f — вектор массовых сил (сил плавучести в данной задаче). В уравнении (3) не учитывается вязкая диссипация. Уравнения в тензорной форме и обобщенной системе координат содержит статья [5] c подробной расшифровкой и выводом всех слагаемых.

В кольцевой системе, как и в цилиндрической, базис ортогональный и отличается переменной длиной базисного вектора e z : | e z | = 1/(1 + (r/R)cosф). Для сокращения записи формул введен параметр A: A = 1 + (r/R) совф. Окончательные уравнения в кольцевой системе координат [5] отличаются по форме от уравнений в ЦСК наличием добавочных слагаемых, в которые входит радиус кривизны R (параметр A ). Так, в уравнении неразрывности (1) слева добавляется слагаемое:

AR

V r СО8ф - V ^Ф sinф + r    СО8ф I .

∂z

В левой (конвективной) части трех уравнений для проекций импульса (2) появляются члены:

i = 1:

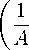
Л z dVr ^Со        2

V dz AR ⁽ V ) ’

i = 3:

A ^-

i = 2:

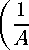
1) V '     + ^ (V z ) ² ,

∂z AR

1 / V^Z“T“ +th(V r совф - V^Фsinф). ∂z AR

В (5) – (7) первые слагаемые связаны с изменением модуля базисного вектора e z , вторые представляют собой добавочные компоненты инерционных сил, возникающих в кольцевой системе координат, а именно центробежная и кориолисова силы. Эти силы компенсируются градиентом давления, добавочный член которого в правой части уравнения для проекции импульса (2) имеет вид:

i =3:

A

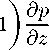
Уравнение сохранения энергии (3) в левой (конвективной) части получает только одно слагаемое:

A

1) v ■ F

∂z

Дополнения (5) – (9) вносят наиболее существенный вклад в уравнения.

Ниже приводятся добавочные члены из правых частей уравнений движения (2) для компонент силы вязкости цд^{к т} (V m ) ,_k ; коэффициент т внесен под знак производной для последующего перехода к безразмерным уравнениям — уравнениям Рейнольдса:

i = 1:

∂

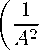
∂z

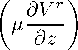
еовф RA ²

( d(^V z ) ∂z

∂V z    µ ∂V r d Г rA^ С'

V ^ф   1 dV r\

V - Г1ф /^{1П ф}

- R 2 A 2 ⁽ V r ^со8 Ф - V ^{Ф з1п} ф ) ,

i = 2:

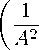
Л d / dV^ф\ s1_W/d(^Vz) J dZrlTГ RA2\ dz

dV ^z\ т /dV ^ф      VV^r 1dV^ф\ . A

+^Z~Г RA   'V ⁺ Г1ф/^1WJ⁺

⁺ 1АГИ ^{( v} r ^Cos G ^{V ф s1} nф) ^, R ² A ²

i = 3:

∂

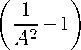
∂z

∂V ^z

µ

∂z

⁺ RA ²

∂ ∂

I v ( t ( V со1ф — V ^Ф 8Шф))+тт- (V со1ф — V ^Ф 11пф) ) + ∂z                      ∂z

т /dV ^z      1 dVz .

⁺ RA[~dr-' ~г1ф s'

µ

R ² A ²

V z .

В уравнении сохранения энергии (3) справа появляются новые слагаемые:

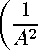
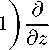
∂T λ ∂T

⁺ ,-■

1 dT .

“У sm ф r ∂φ

При использовании двухпараметрической модели турбулентности, например (к — е) [17] , в кольцевой системе

координат уравнения ЦСК также нужно дополнить новыми слагаемыми. Поскольку уравнения сохранения для

скалярных величин k и ε по типу похожи на уравнения сохранения энергии (3) , то и добавочные члены можно

записать в виде, аналогичном (9) и (13) . Таким образом, в левой (конвективной) части уравнений для f = {к,е}

добавится только по одному слагаемому:

1) v z df.

∂z

В правых же частях уравнений новые члены содержат слагаемых значительно больше:

±6^f + ^C^f о . —

A ²     ∂z ∂z RA ∂r

1 df-   } sm Ф .

r ∂φ

В уравнениях (k - ε) модели в слагаемых, обуславливаемых «генерацией» турбулентности [17] , тоже появляются дополнительные члены, связанные с кривизной, но в данной работе они в расчет не принимаются.

Большое число добавочных слагаемых в диффузионных уравнениях не должно смущать. Многие из них в практических задачах (при A, близком к 1) очень малы и ими можно пренебречь. Например, слагаемые, в которые входит производная по длине трубы d/dz, заметно отличны от нуля только на начальном (гидродинамическом/термическом) участке. В турбулентных потоках начальные участки (длиной 5–10 калибров) малы по сравнению с участками стабилизации (50–100 калибров и более). Конечно же в кольцевой системе координат, как и в ЦСК, в дополнительных слагаемых присутствуют члены с множителем 1/r. Поэтому в ячейках расчетной сетки, примыкающих к центру кольцевой области, надо принимать такой алгоритм осреднения по их объему, чтобы исключить деление на нуль.

4. Численный расчет

Уравнения (1) – (3) для вычислений приводились к безразмерному виду:

– уравнение движения

( V -V ) V = —V p * +      (1+ et ) V V )+ Grieg*;

– уравнение энергии

1 / Рг \

^{( v} - ^{v ) e} =4 ¹⁺ рг / t ^e

Здесь p ^∗ — динамическое давление, отнесенное к масштабу ρV 0² ; ε t — коэффициент турбулентной вязкости; Re = V ₀ d/v — число Рейнольдса; Gr q = (g(3q_wd ⁴ /v 2 — число Грасгофа; Pr — число Прандтля; Pr t = e _t /e _q — турбулентное число Прандтля; О = (T — T ₀ )/(q _w d/A ) — безразмерная разность температуры; Pe = RePr — число Пекле. В этих выражениях g * = g /g есть безразмерный вектор силы тяжести, где g — ускорение свободного падения; ν — кинематический коэффициент вязкости; λ — теплопроводность; β — коэффициент термического

расширения; q _w — плотность теплового потока на стенке внутренней трубы; ε _q — коэффициент турбулентного переноса тепла; T — температура жидкости; T 0 — температура на входе в трубу. Масштаб для координат r и z принимался равным внутреннему диаметру трубы d= 2r 0 . Компоненты вектора скорости V относились к средней по сечению канала скорости V 0 .

На входе в трубу профиль скорости считался единичным: | V | = 1, а безразмерная температура нулевой: Θ = 0. На выходе из канала обеспечивалось условие постоянства расхода, а температура определялась из условия теплового баланса. Тепловой поток на внутренней стороне стенки в безразмерном виде задавался выражением: q w * = 1/Pe(d0/dR) w = — 1/Pe. Участку обогрева длиной 80d предшествовал участок гидродинамической стабилизации 20d. Турбулентное число Прандтля принималось равным Pr t = 1.

Расчетная сетка внутри трубы имела, соответственно, размеры N r х N _ф х N z = 50 х 50 х 450 и вблизи стенок сгущалась. На толщину стенки из нержавеющей стали приходилось еще 5 ячеек.

Система уравнений (16) , (17) в совокупности с уравнением неразрывности (1) решалась методом контрольного объема в открытом коде ANES20XE [18] , предназначенном для численного моделирования процессов гидродинамики и тепломассообмена. Для коэффициента турбулентной вязкости ε t использовалась модель (k — е) с пристеночными функциями [17] . Учитываемые дополнительные слагаемые вводились в расчет системы дифференциальных уравнений в виде функций источниковых членов.

В расчетах учитывалось также влияние сил плавучести, возникающих при свободной конвекции, определяемых числами Грасгофа: Gr q = (0.34 v 0.7) • 10 8 , что соответствовало двум значениям q w , кВт/м ² : 15 и 30.

Варьирование размеров сетки в сторону уменьшения или увеличения в 1.5 раза приводило к изменениям расчетных величин скорости не более, чем на 0.5%.

• 5.    Результаты численного и натурного экспериментов

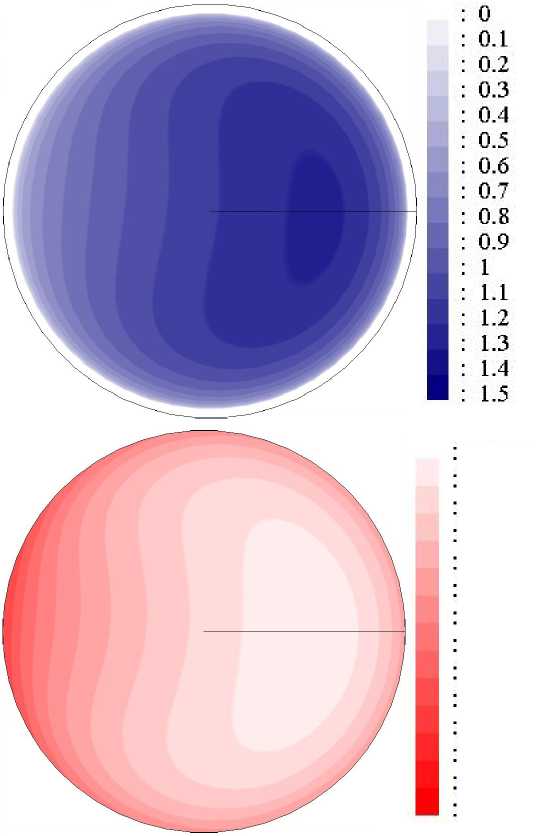
  Рассмотрим режим течения с числом Рейнольдса Re = 35000 обогревом с q w = 15 кВт/м ² (Gr q = 0.35 • 10 8 ). Исследуемое сечение трубы удалено от входа в зону обогрева на расстояние z = 76 d . На рисунке 3 представлены поля продольной компоненты скорости V ^z (Рис. 3а , б ), безразмерной разности температуры Θ (Рис. 3в , г ), векторное поле вторичных течений ( V ^r , V ^φ ) (Рис. 3д ) и поле безразмерной интенсивности пульсаций температуры σ ^∗ = σ/ ( qd/λ ) (Рис. 3е ), σ ² — дисперсия. Поток находится в поле центробежной силы, действующей в горизонтальной плоскости, и прижимающей поток к периферии, то есть к стенке. Это приводит в поперечном сечении к появлению вторичных течений в виде двух симметричных вихрей с осями, параллельными оси трубы (см. Рис. 3д ). При этом исчезает осевая симметрия полей осредненных скорости и температуры, о чем свидетельствуют профили на рисунках 4 и 5, построенные по горизонтальной ( X ) и вертикальной ( Y ) осям, а распределение температуры стенки (Рис. 6) становится неоднородным по периметру сечения c минимумом и максимумом вблизи угла φ , равного 0 и 180.

( a )

Рис. 3. Поля безразмерной продольной компоненты скорости V ^z ( а , б ), безразмерной разности температуры Θ ( в , г ), векторное поле вторичных течений ( V ^r , V ^φ ) ( д ), поле безразмерной интенсивности пульсаций σ ^∗ ( е ) в сечении z/d= 76 при Re = 35000 и q w = 15 кВт/м ² ( Gr q = 0.35 · 10 ⁸ ); расчетные ( а , в , д ) и экспериментальные ( б , г , е ) данные

( в )

: -0.04

: -0.02

: 0

: 0.02

: 0.04

: 0.06

: 0.08

: 0.1

: 0.12

: 0.14

: 0.16

: 0.18

: 0.2

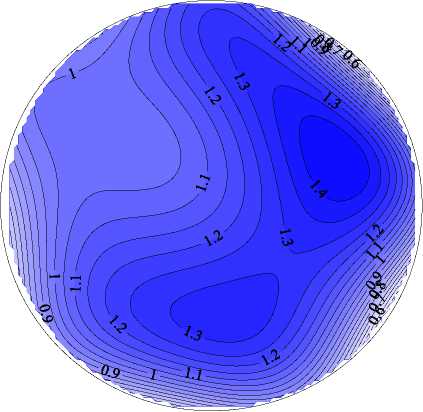
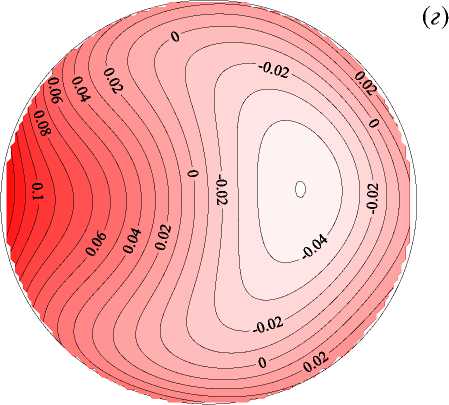
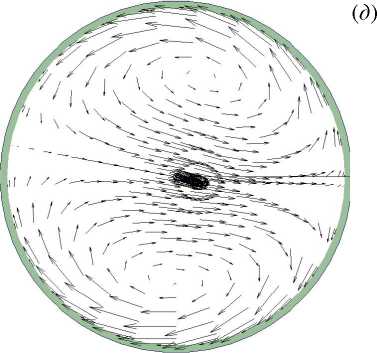
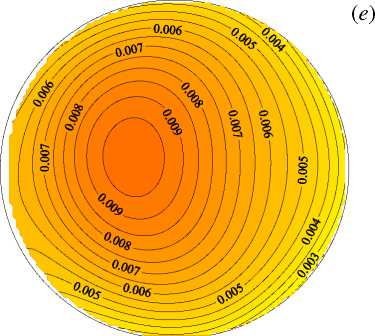
Рис. 3. Продолжение

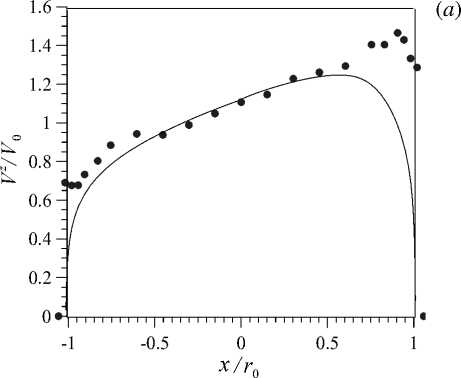
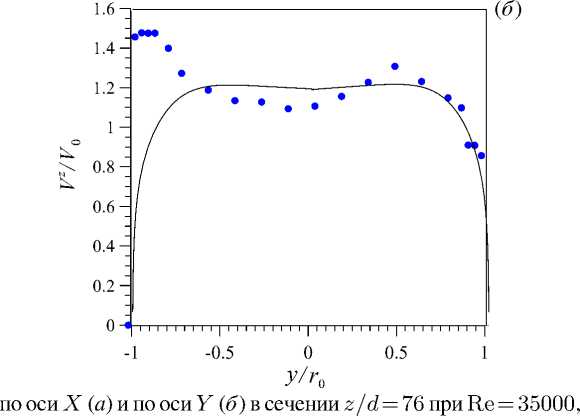
Рис. 4. Профили безразмерной продольной скорости V ^z q w = 15 кВт/м ² ; линии – расчет, точки – эксперимент

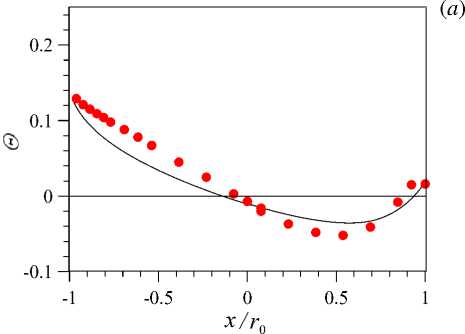
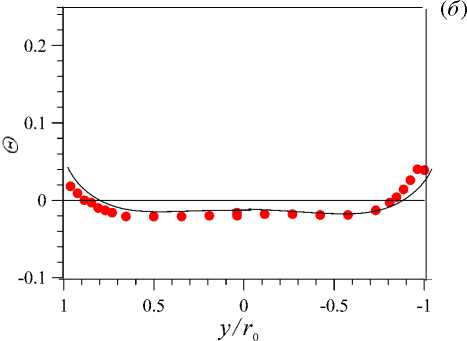
Рис. 5. Профили безразмерной температуры Θ по оси X ( а ) и по оси Y ( б ) в сечении z/d = 76 при Re = 35000 , q w = 15 кВт/м ² ; линии – расчет, точки – эксперимент

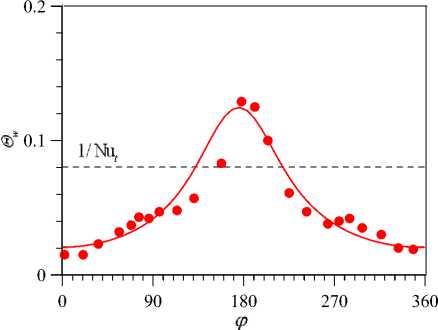
Рис. 6. Распределение безразмерной температуры стенки Θ w по периметру в сечении z/d = 76 при Re = 35000 , q w = 15 кВт/м ² ; линии – расчет, точки – эксперимент; горизонтальная штриховая линия – теоретическое значение безразмерной температуры стенки

На рисунках, кроме данных, полученных путем моделирования, для сравнения представлены результаты опытов. Рассчитанные профили скорости удовлетворительно согласуются с измеренными, если учитывать относительную погрешность измерений, которая оценивалась в пределе 7%.

Следует отметить, что метод измерения плохо показывает себя около стенки вследствие принципиальных трудностей: вблизи стенки, в отличие от ядра потока, не выполняется гипотеза «замороженной» турбулентности, на чем, собственно, и основан корреляционный метод измерения [16] . Совпадение оказывается лучшим у данных по температуре: расчетные и опытные профили и поля хорошо согласуются между собой как количественно, так и качественно.

Данные по локальной теплоотдаче на рисунке 6 обладают наибольшей практической значимостью, а совпадение максимума и минимума подтверждает адекватность расчетной модели. Горизонтальной линией показано теоретическое значение безразмерной температуры стенки Θ w = 1/Nu t при развитом турбулентном течении в прямой трубе, применимой для ЖМ теплоносителей. Турбулентное число Нуссельта рассчитывается по формуле Лайона: Nu t = 7 + 0.025Pe ^0.8 [19] . Как видно, в изогнутой трубе локальные характеристики теплоотдачи далеки как от средних значений по периметру сечения, так и от теоретических для прямых труб.

В представленном выше режиме течения влияние гравитации, то есть сил плавучести, на поток незначительно. Рассмотрим далее такой режим, при котором проявление этих сил велико. Оценить, насколько сильны эффекты плавучести по сравнению с инерционными силами в потоке, помогает число Ричардсона Ri= Gr/Re ² . С ростом плотности теплового потока на стенке (Gr), либо со снижением числа Рейнольдса число Ричардсона увеличивается. Так, Re = 35000 соответствует Ri = 0.06. Ниже приводятся данные, полученные в режиме с меньшим числом Рейнольдса (Re = 20000) и большей плотностью теплового потока (q w =30 кВт/м ² ), которым отвечает Ri = 0.18.

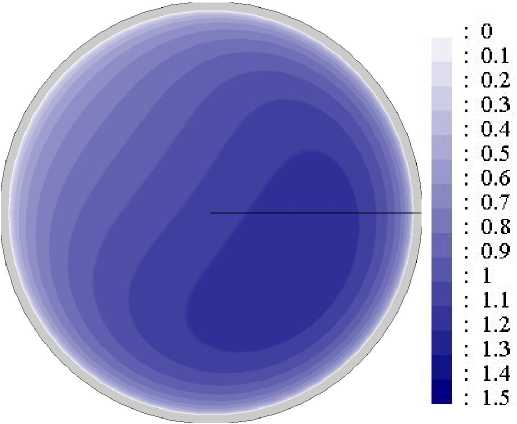
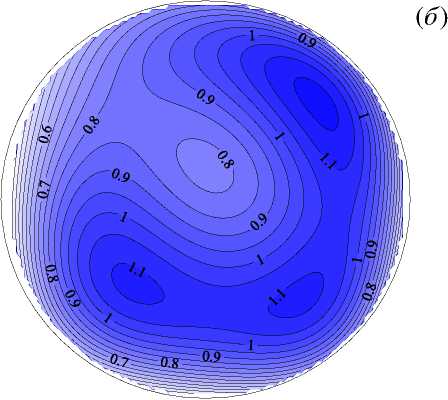
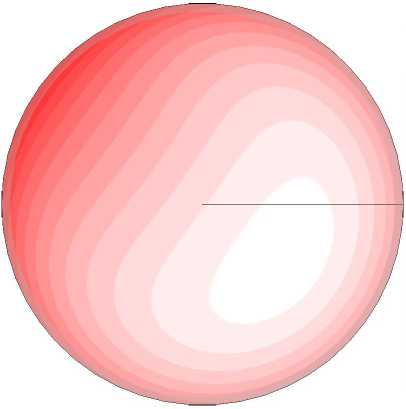
На рисунках 7 –10 показаны поля и профили безразмерных продольной скорости и температуры, структура вторичных течений и интенсивности пульсаций температуры в присутствии сил плавучести. Как известно [20, 21] , под влиянием сил плавучести при течении в горизонтальной обогреваемой трубе в потоке тоже появляются два симметричных вихря с осями, параллельными оси трубы. В поперечном сечении трубы конфигурация вторичных течений, вызванных центробежными и термогравитационными силами, аналогична, с той лишь разницей, что плоскости их поперечной симметрии в этих случаях перпендикулярны друг другу. Картины вторичных течений и воздействие последних на поля скорости, температуры и характеристики теплоотдачи авторами статьи получены также в экспериментах на горизонтальных прямых трубах [20, 21] . Результаты для Re, равных 20000 и 35000, в общем аналогичны, за одним исключением: в кольцевой трубе конкуренция сил различной природы — инерционных и термогравитационных — приводит к повороту картины вторичных течений относительно вертикальной или горизонтальной оси (Рис. 7д ). Соответственно положение максимумов и минимумов скорости и температуры также смещаются по углу в поперечном сечении трубы.

( a )

: -0.06 ( в )

: -0.04

: -0.02

: О

: 0.02

: 0.04

: 0.06

: 0.08

: 0.1

: 0.12

: 0.14

: 0.16

: 0.18

: 0.2

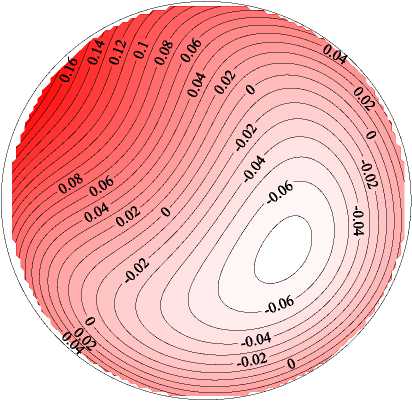
Рис. 7. Поля безразмерной продольной компоненты скорости V ^z ( а , б ), безразмерной разности температур Θ ( в , г ), векторное поле вторичных течений ( д ) и поля безразмерной интенсивности пульсаций температуры σ ∗ ( е ) в сечении z/d= 76 при Re= 20000 и q w =30 кВт/м ² ( Gr q = 0.7 · 10 ⁸ ); расчетные данные ( а , в , д ), опытные – ( б , г , е )

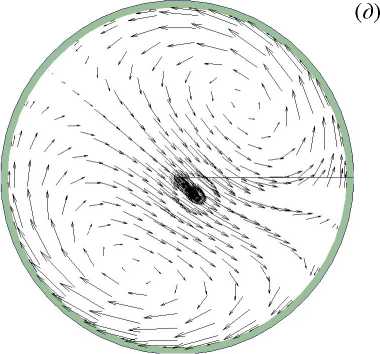
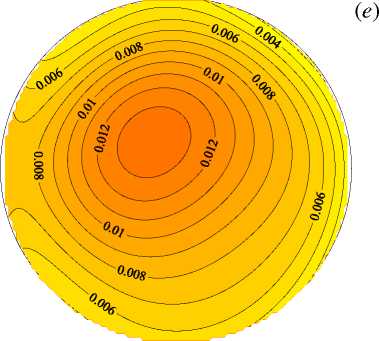
Рис. 7. Продолжение

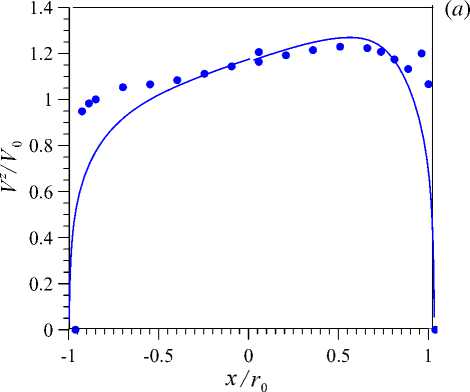
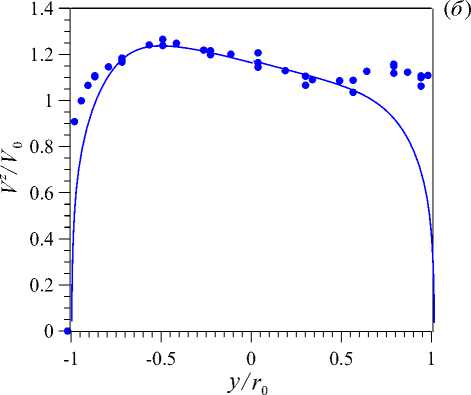
Рис. 8. Профили безразмерной продольной скорости V ^z по оси X ( а ) и по оси Y ( б ) в сечении z/d= 76 при Re= 20000 и q w = 30 кВт/м ² ; линии – расчет, точки – эксперимент

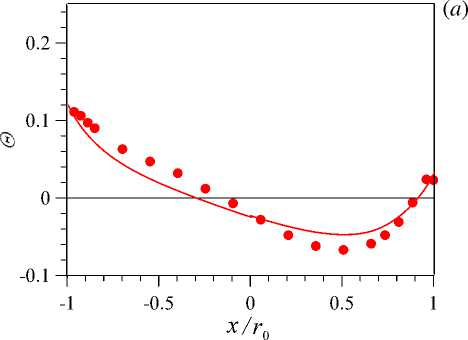
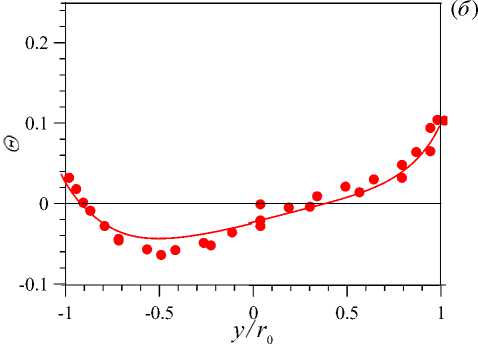
Рис. 9. Профили безразмерной температуры Θ по оси X ( а ) и по оси Y ( б ) в сечении z/d = 76 при Re = 20000 и q w =30 кВт/м ² ; линии – расчет, точки – эксперимент

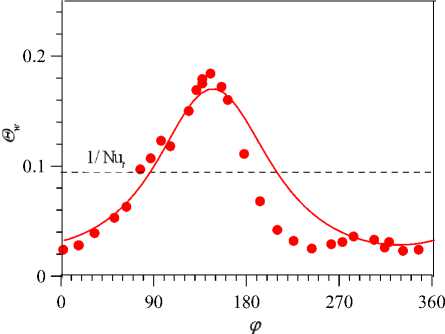
Рис. 10. Распределение безразмерной температуры стенки Θ w по периметру в сечении z/d = 76 при Re = 20000 , q w = 30 кВт/м ² : линии – расчет, точки – эксперимент; горизонтальная штриховая линия – теоретическое значение безразмерной температуры стенки

На рисунке 8б совпадение профилей скорости удовлетворительное, за исключением точек вблизи стенки, что может быть связано с методическими трудностями проведения эксперимента и, возможно, с недостатками методики расчета. Во-первых, модель турбулентности, которая является полуэмпирической, а не универсальной. Во-вторых, в расчеты заложено граничное условие нулевой скорости на стенке. Имеют место сомнения в справедливости гипотезы прилипания ртути при течении в трубе, которые вызваны тем фактом, что снижение скорости потока вблизи и непосредственно при касании датчиком стенки не наблюдается. Тем не менее, совпадение температурных данных хорошее, что связано с особенностями ЖМ теплоносителей: теплообменные характеристики мало чувствительны к гидродинамическим, то есть изменение профиля скорости почти не сказывается на профилях температуры, характерными для теплоносителей с малыми числами Прандтля [19] .

0.25

0.2

0.1

0.05

-0.05

I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I 0        500      1000      1500      2000

Pe

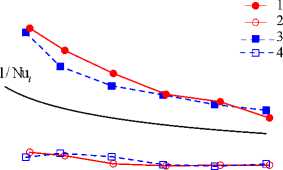
Аналогичные данные получены при числах Рейнольдса 11000, 50000, 65000, 80000. Результаты сравнения с экспериментом удовлетворительные. На рисунке 11 показаны максимальные и минимальные значения безразмерной разности температуры стенки Θ w , вдали от входа в зону обогрева, в зависимости от числа Пекле Pe. На рисунке представлены экспериментальные и расчетные данные для соответствующих режимов и график 1/Nu t , справедливый для стабилизированного турбулентного теплообмена при течении ЖМ в прямых трубах [18] . Как видно из рисунка 6, локальные значения температуры на стенке значительно отличаются и от средних, и от теоретических. Совпадение опытных и расчетных данных хорошее (в пределах погрешности эксперимента).

Рис. 11. Зависимость безразмерной максимальной (линии 1 , 3 ) и минимальной ( 2 , 4 ) температуры на стенке трубы Θ w в сечении z/d = 76 при q w = 30 кВт/м ² : – эксперимент ( 1 , 2 ) расчет ( 3 , 4 )

Итак, изгиб трубы приводит к появлению горячего пятна — области, в которой температура стенки значительно выше осредненной по периметру сечения, а также превосходит значения, рассчитанные для прямой трубы. Наблюдаемая неоднородность в распределении температуры стенки есть следствие как закрутки потока, так и влияния свободной (термогравитационной) конвекции, свойственной теплообмену в трубах. Этот факт требуется учитывать и в теплогидравлических, и в прочностных расчетах. Возникающие в изогнутых трубах дополнительные напряжения могут привести к деформации, к усталостному разрушению термонагруженных стенок труб в реальных теплообменных устройствах.

• 6.    Заключение

Анализ полученных результатов позволяет сделать выводы.

Впервые проведены численные и экспериментальные исследования гидродинамики и теплообмена при неизотермическом течении жидкого металла (ртути) в горизонтальном участке кольцевой трубы с внутренним диаметром 19 мм, длиной около 100 калибров, имеющей изгиб радиуса 0.5 м. Расчеты и эксперименты проведены в диапазоне чисел Рейнольдса Re=11000 ^ 80000 и обогрева с q w = 10 ^ 30 кВт/м ² (Gr q = (0.2 ^ 0.7) • 10 8 ).

Задача решалась численно в дифференциальной постановке, включающей уравнения сохранения массы, импульса и энергии, записанные в кольцевой системе координат для условий, соответствующих эксперименту. При выводе уравнений за основу взята система уравнений в цилиндрической системе координат, в которую для учета перехода к кольцевым координатам введены добавочные слагаемые в виде источниковых членов, построенных авторами ранее (см. статью [5] ).

Для реализации использован наиболее общий метод, позволяющий получить точное решение задачи на основе уравнений, представленных в тензорном виде в обобщенной криволинейной системе координат. В отличие от других методов, также прибегающих к преобразованиям координат, например, декартовой системы в криволинейную, и теряющих при этом некоторые слагаемые, данный метод таких недостатков не имеет. При этом геометрия расчетной области при переходе к изогнутой трубе не меняется — это прямая труба. В численном решении для описания турбулентности применялась модель (к — е) с пристеночными функциями.

В экспериментах использовался зонд с микротермопарным датчиком на конце. Зонд одновременно измерял профиль и поле средней продольной скорости корреляционным методом и осредненную температуру в поперечном сечении трубы, удаленном от входа и находящемся в области стабилизированного теплообмена.

Сравнение расчетных и экспериментальны данных показало удовлетворительное совпадение по профилям скорости и хорошее — по распределению температуры в потоке. Обнаружено влияние двух факторов на течение и теплообмен ЖМ при кольцевом изгибе трубы — инерционных центробежных и термогравитационных сил: в их присутствии нарушается осевая симметрия потока и наблюдается сильная неоднородность в распределении температуры стенки по периметру сечения трубы.

Результаты сравнения расчета и эксперимента подтверждают работоспособность метода расчета в кольцевой системе координат. Преимущество предложенной методики заключается в простоте описания геометрии расчетной области, поскольку появляется возможность использовать структурированную расчетную сетку. Упрощается задание граничных условий (границы расчетной области проходят по координатным поверхностям), изменение геометрии задается только одним параметром (радиусом изгиба), удобным становится вывод результатов для анализа и последующей обработки. Все это существенно экономит вычислительные ресурсы, сокращает время расчета и способствует получению более надежных расчетных данных.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации в сфере научной деятельности на 2023–2025 гг., исполнители Лучинкин Н.А., Разуванов Н.Г. (Государственное задание № 075-00269-25-00) и Полянская О.Н. (Государственное задание № FSWF-2023-0017, Соглашение № 075-03-2023-383 от 18 января 2023 г.).