Численное интегрирование

В статье предложена модификация численных методов интегрирования систем обыкновенных дифференциальных уравнений, учитывающих физическую природу этих уравнений, т. е. наличие интегралов, а именно: численные методы интегрирования систем обыкновенных дифференциальных уравнений, обладающих кососимметрической матрицей коэффициентов при линейных членах.

Модифицированные методы являются более точными, чем исходные методы Рунге — Кутты, Адамса — Штермера и др., и более предпочтительными в задачах интегрирования на больших промежутках. Точность модифицированных методов обусловлена тем, что они сохраняют интеграл однородной системы - свойство ортогональности фундаментальной матрицы.

Рассмотрим линейную систему

X = A(t)X,                (1)

где X = ( х ^ ..., х_п ) , А ( t ) — кососимметрическая ( и х и ) — матрица. Условия теоремы существования и единственности мы будем считать выполненными. Решение задачи Коши X = Х_о при t = 0 дается формулой

X(t) = 2(t)X0,              (2)

где Е ( 1 ) — фундаментальная матрица, удовлетворяющая соотношениям

Е = A ( t )E, Е ( о ) = Е .

Известно [4], что Е ( t ) является унитарной матрицей, т. е. выполняется соотношение

2 ( 1 ) 2 * ( 1 ) = Е .               (3)

Предполагаемая модификация численных методов заключается в таком их изменении, что соотношение (3) будет выполнено для всей последовательности приближенных значений 2к фундаментальной матрицы в узлах tk = kh, причем это изменение произ водится в пределах локальной точности метода, что, очевидно, не ухудшает его.

Пусть А — заданная невырожденная ( п х п ) матрица. Требуется найти симметрическую положительно определенную матрицу F и ортогональную матрицу U такие, что выполняется соотношение

А = FU . (4)

Введем в рассмотрение множество Мп квадратных матриц порядка п и множество Dn невырожденных матриц того же поряд ка. Множество Мп является линейным нормированным пространством с нормой, определяемой соотношением [6]

||С|| = max И, " " ХеЕ_п ||А||

где С е М_п , X е Е_п .

На множестве М_п можно задать динамическую систему, определяемую матричной системой дифференциальных уравнений

X = F(X,t), (6)

где X , F е М ; для F выполнены условия, обеспечивающие существование, единственность и продолжимость на интервале ( t o , да ) решений; точка обозначает дифференцирование по параметру t .

Поставим следующую задачу: построить такую дифференциальную систему вида (10), что решение задачи Коши с начальным усло-

вием X = Х о при t = t o = 0 сходится к значению матрицы U полярного разложения (8). Таким образом, мы сведем первоначальную задачу к численному интегрированию построенной системы дифференциальных уравнений [3].

Рассмотрим матричное дифференциальное уравнение

X = ¹ ( - X + X *^{- 1} ) .            (7)

Обозначим X ( t, Х о ) решениесистемы (7), удовлетворяющее начальному условию X = Х о при t = 0.

Теорема 1. Если матрица начальных условий Х о невырожденная, то решение X ( t , Х _о ) системы (7) также будет невырожденной матрицей при t >  0, причем решение X ( t , Х о ) неограниченно продолжимо при t >  0.

Доказательство. Сначала покажем, что при t >  0 выполняется условие

X ( t , Х о ) е D „ . (8)

Предположим противное, а именно: пусть существует момент времени tp в который выполнено соотношение det(X(t1,Хо)) * о. Тогда справедливо равенство det (х (tbХо)X* (tbХо))* 0. (9)

Введем в рассмотрение матричную функцию V = XX * , заданную в М_п . Эта функция удовлетворяет на решениях системы (7) следующему уравнению:

V = - V + Е . (Ю) Интегрируя, получаем

V = ( V o - Е ) exp ( - t ) + Е. (И)

В силу того что матрица V) = Х о Х о является симметрической и положительно определенной, из формулы (1о) следует, что при t >  0 определитель матрицы V не обращается в нуль, что находится в противоречии с формулой (8), которое и доказывает справедливость условия (8) [1].

Необходимым и достаточным условием продолжимости решений системы (7) являет- t ся расходимость интегралов J-v^dvjj.

о

Из (9) имеем

t

J V yj ^{d l} yj = ^—1н ( V yj ^— ф у j о ,

о где буу — символ Кронеккера [2].

Расходимость интеграла следует из формулы (1о), так как из нее вытекает v ^y ^ б уу , и выражение в правой части последнего соотношения не ограничено. Теорема доказана.

Теорема 2. Решение X ( t, Х о ) системы (7) с начальным условием Х о = А сходится при t ^ да к значению матрицы U полярного разложения (4), причем справедлива оценка

||X ( t, А ) - U|| < | АА * - Е| exp ( - t ) . (12)

Доказательство. Поскольку решение X ( t, А ) представимо единственным образом в виде

X ( t, А ) = F ( t ) U ( t ) , (13)

где F ( t ) , U ( t ) — матрицы полярного разложения. Отметим, что F ( о ) = F, U ( о ) = U. Подставляя выражение (12) в уравнение (7), можно получить следующее соотношение:

F (t) F (t) + F (t) U (tX (t) F (t) = = F(t)U (t)U* (t) F(t) + F (t) F(t).

Из (1о) следует, что матрица F (t) представляет собой ряд по целым отрицательным степеням экспоненциальной функции параметра t с коэффициентами, являющимися постоянными симметрическими матрицами:

F ( t ) = Е + 2 (f² - Е ) e ^{- t} -

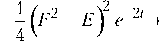
Следовательно, имеет место тождество

F ( t ) F ( t ) = F ( t ) F ( t ) .         (15)

Рассматривая совместно выражения (13), (14) и условие ортогональности

U ( t ) U* ( t ) + U ( t ) U * ( t ) = 0, получаем, что имеет место соотношение

U ( t ) = 0 или U ( t ) = const = U .

Поскольку ||f ( t ) - f|| ^ 0, в силу (10) справедливо следующее утверждение:

||X ( t, Л ) - U| ^ 0 при t ^ те.

Оценку (11) получаем следующим образом. По свойству нормы (5) можно выписать цепочку равенств и неравенств

II X ( t, л ) - Ц = ||( ^F ( ^t ) - E)U ( ^t )|| <

^ ilF (t) - Ell=|(f2 m -E )(F (t)+E1 <

< |f² ( t ) - e| = |f² - e| exp(- t ) =

= ||лл* - e|| exp ( - t ) .

При оценке нормы ||f² ( t ) - f|| мы использовали выражение (10). Теорема доказана.

На основании доказанных теорем можно утверждать, что значение матрицы U можно получить, численно проинтегрировав систему (7) с начальным условием X 0 = Л при t = 0. Точность нахождения матрицы U будет зависеть как от длины интервала интегрирования, так и от точности самого метода интегрирования [5].