Численное исследование бифуркаций при спиральном течении жидкости со свободными границами

Предлагаемая работа посвящена исследованию плоских стационарных течений вязкой несжимаемой жидкости со спиральными линиями тока. Впервые этот класс решений был открыт Г. Гамелем [1], аналогичные решения несколько более общего вида описаны Озееном [2] и Розенблаттом [3]. В современном изложении эти работы проанализированы в [4]. Исследование решений уравнений Навье–Стокса со спиральными линиями тока позднее было продолжено в работах В.В. Пухначева [5–7]. В частности, им замечено, что данные решения можно получить с использованием групповых свойств уравнений Навье–Стокса и рассматривать как течения со свободными границами.

2.    Постановка задачи

Основными искомыми функциями при описании течения вязкой несжимаемой жидкости являются вектор скорости V и давление P . Исследование групповых свойств уравнений Навье–Стокса [5] показало, что они допускают стационарное инвариантное решение вида:

V r = -u (Ю,   V _e=- v©,    P = p— p (&                      (1)

• rrr ²

где V r , V ₉ — проекции вектора скорости на оси полярной системы координат, связанной с соответствующей декартовой системой соотношениями: r = ^x 2 + x 2 , 9 = arctg ( x ₂ / x , ) . Здесь v — кинематическая вязкость, р — плотность жидкости. Переменная ^ зависит от полярных координат и имеет вид:

^ = 9 + Щп ( г/r ,) ,

где r₀ >  0 — постоянная с размерностью длины, ц — некоторый параметр задачи, значение которого будет определено ниже.

Подставляя выражения (1) в систему Навье–Стокса, записанную в полярных координатах, и исключая v( ^ ) и p ( Е ), получаем уравнение для искомой функции и ( Е ):

(ц +1) и — 4ц и + 4 и + и — 0.

Заметим, что Е — const соответствует логарифмическая спираль, лежащая в плоскости полярных координат. Потребуем, чтобы логарифмическая спираль Е — Y (здесь у — const, 0 < у < 2п) была свободной границей, тогда из кинематического условия на свободной границе будем иметь ци + v — 0.

Следовательно, вторая искомая функция v( ^ ) определяется из соотношения:

v — —ц и .

Динамическое условие на свободной границе принимает вид:

( ц ² + 1) и ‘ — 2 ц и — 0 .

Если полагать, что логарифмическая спираль Е — 0 является твердой стенкой, то из условия и (0) — 0 , с учетом (2), следует, что на границе Е — 0 выполняется условие прилипания. Введем обозначения

Y-ц ln ( r/r )

Q — J   rV_rd 9 ,

-ц ^ln ( r/r G )

Y ^ц ln ( r/r j )

Л — J    rV ₉ d 9 .

-ц ^ln ( rr )

Здесь Q есть расход жидкости через начало координат, а Л — циркуляция скорости по дуге окружности r — const, заключенной между границами. В силу соотношений (1) и (2) введенные величины соотносятся как Л/ Q — —ц , что придает простой физический смысл параметру ц . Вторым определяющим параметром естественно считать число Рейнольдса Re — Q /у. Из определения Q и V r следует:

Y

J и ( Е ) d Е — Re. Таким образом, нахождение вектора скорости V вязкой несжимаемой жидкости в случае 0

стационарного течения со спиральными линиями тока существенно упрощается, и вместо решения системы уравнений Навье–Стокса требуется найти решение обыкновенного дифференциального уравнения второго порядка в области, имеющей свободную границу.

Хотелось бы изучить влияние параметров Re и ц . С этой целью рассмотрим следующие задачи.

Задача А. Требуется определить скорость течения жидкости в области, ограниченной твердой стенкой и свободной границей в виде логарифмических спиралей; расход через начало координат задан.

Имеем одномерную задачу с неизвестной границей, в которой, варьируя Re и ц , необходимо найти функцию и ( Е ) и число y ^е (0, 2 п ), удовлетворяющие соотношениям:

( ц² + 1) и " — 4 ц и ' + 4 и + и ² — 0 при 0 ;

( ц ² + 1) и '- 2 ц и — 0 при е —y ;

• < и — 0 при е — 0;

  
  

Y

J и ( Е ) d Е — Re.

_ 0

После определения и ( Е ) вторая искомая функция v( E ) отыскивается из равенства (2).

Задача В. Необходимо определить скорость течения жидкости в области, ограниченной двумя свободными границами в виде логарифмических спиралей, с известным расходом через начало координат.

Задавая параметры Re и ц , приходим к следующей одномерной задаче с неизвестной границей, в которой требуется найти функцию и © и число у е (0, 2 п ) такие, чтобы выполнялись соотношения:

( ц ² + 1) и" - 4 ц и ' + 4 и + и ² = 0 при 0 <^<у ;

( ц ² + 1) и '- 2 ц и = 0,     ^ = 0,    ^ = у ;

1} f и © d ^ = Re.

_ 0

После определения и © вторая компонента вектора скорости у© отыскивается из равенства (2).

Согласно цели работы посмотрим далее, в какой зависимости находится существование и количество решений рассматриваемых задач от значений параметров Re и ц .

3.    Алгоритм численного исследования

При численном решении проще решать краевую задачу, а не задачу со свободной границей. В обсуждаемом случае можно легко перейти к краевой задаче. Для этого будем считать параметрами ц и у , а Re — искомым числом. Задавая у е (0, 2 п ), из первого уравнения и двух граничных условий системы (3) (или, в зависимости от решаемой задачи, (4)) определяем искомую функцию и ©, а затем из интегрального соотношения находим Re . Таким образом, необходимо изучить разрешимость следующих задач:

Задача А1: найти функцию и © (при этом у известно), являющуюся решением краевой задачи:

( ц² + 1) и "- 4 ц и ' + 4 и + и ² = 0,   при 0 <^<у ;

( ц ² + 1) и '- 2 ц и = 0   при ^ = у ;

и = 0 при ^ = 0.

Задача В1: найти функцию и © (при этом у известно), удовлетворяющую краевой задаче:

[ ( ц ² + 1) и" - 4 ц и ' + 4 и + и ² = 0 при 0 <^<у ;

[ ( ц ² + 1) и '- 2 ц и = 0 при £ = 0, £ = у .

Исследуем существование и количество решений задач A1, В1 в области параметров ц и у ( у е (0, 2 п )).

Рассмотрим случай ц = 0. При этом поставленные задачи переходят в уже изученные [7]: в задачу течения жидкости между твердой стенкой и прямолинейной свободной границей; в задачу течения между двумя прямолинейными свободными границами. В работе [7] показано, что в зависимости от значения параметра у может существовать от одного до семи различных ненулевых решений. Поскольку решение задачи В1 при ц = 0 выражается через полные эллиптические интегралы первого и второго рода [7], то при разработке алгоритма численного исследования тестовой служила именно эта задача.

Расчеты проводились в пакете “Wolfram Mathematica 9.0”, установленном в Информационновычислительном центре НГУ (г. Новосибирск). Для решения краевых задач применялся метод «стрельбы».

Проблема численного исследования заключается в нахождении нескольких решений, удовлетворяющих одним и тем же краевым условиям. Для разделения этих решений, помимо двух данных условий на границах, необходима дополнительная информация о приближенном значении искомой функции на одной из границ. При тестировании алгоритма с ц = 0 в качестве такой дополнительной информации использовалось значение на границе £ = 0 аналитически найденных точных решений. При этом относительная погрешность вычислений составила порядка 1%.

Для нахождения решений в области ц ^ 0 осуществлялся сдвиг по параметру ц от линии ц = 0 с шагом ц = 0,01. При этом в качестве дополнительной информации бралось значение искомой функции либо на границе с = у (для задачи А1), либо на границе ^ = 0 (для задачи В1) при значении параметра ц , взятом с предыдущего шага.

4.    Линии бифуркации и решения линеаризованной задачи

Для аналитического исследования удобно переписать задачи А1, В1 в эквивалентной форме. Для этого сделаем замену

-             ( 2цМ

-У x ,    u = exp        у ,

(ц ² + 1 )

обозначим 2 цуДц ² + 1 ) = a . Тем самым получаем искомая функция y ( x ):

краевую задачу А2, которой удовлетворяет новая

dx^{2 +}

1 ° _ у = 0

( и 2 + 1 ) 2	- у +	μ 2
при	x =	1;
при	x =	0.

— e ^axy ² = 0;

+ 1

Напомним, что при этом у считается

известным параметром ( у е (0, 2п) ), а Re, в силу последнего

Re

из уравнений (3), находится из условия | е^аху ( x ) dx = —

.

Будем искать для задачи А2 решения вида к задаче Штурма–Лиувилля:

Y

у = е у , где е ^ 0 . Линеаризация системы (5) приводит

I у = 0,     0 <  x <  1;

^{у /+}[ц^+ 1

у = 0 при x = 0;

у ' = 0 при x = 1.

Согласно принципу линеаризации в задачах нахождения точек бифуркации [8] каждое значение ^{ц 2} + 1 Гл.)

уn = —-—I — + пn I, где n = 0,1, 2,... есть точка бифуркации задачи A2. Поскольку параметр у изменяется только в диапазоне у е (0, 2п), количество точек бифуркации конечно, а именно n = 0,1, 2, 3 .

ц² + 1 Гп .    )       „ , „ „

Следовательно, на плоскости параметров ц, у существует четыре линии уn = —-—I — + пn I, n = 0,1, 2, 3 , на которых возникают решения задачи A2: yn = еsin^у + пn| x + 0(е2), где е^ 0. Соответствующие решения задачи A1 имеют вид:

u n = е exp

Таким образом, на каждой линии бифуркации от нулевого решения ответвляются два (одно при е >  0, другое при е <  0) решения вида (6).

Проводя аналогичные выкладки для задачи B1, получаем, что в этом случае в плоскости параметров ц, у существуют три линии бифуркации у,

( ц ² + 1 ) п n

( n = 0,1, 2,3),

на которых возникают решения задачи В1 вида:

u_n = е exp

5.    Результаты численного исследования течения, заключенного между твердой стенкой и свободной границей

Аналитические исследования этой задачи, проведенные при ц = 0 в работе

[7], показали наличие

„ - ,                                          1 f п )

двусторонней бифуркации в точках уп = —I—+ пп I, п = 0,1, 2, 3 . То есть соответствующее стоку в начале координат ( Re — отрицательно), а соответствующее источнику — решение с положительными Re .

В результате численных экспериментов подтвердилось существование

при

при

Y > Y _п есть решение,

Yп

двусторонней

решение,

бифуркации

при у = л/ 4 . В этом случае при у е ( п/4, 2п ) существует решение для отрицательных чисел Рейнольдса, а при y ^е ( 0, п/4) — решение с положительными числами Рейнольдса. В окрестностях остальных точек бифуркации ( y = 3п/4, 5п/4, 7п/4) выявилась несколько иная ситуация, а именно: решение, ответвляющееся от нулевого и соответствующее положительным Re , действительно присутствует, но только при малых отклонениях от точек бифуркации. Интервал наличия такого решения следующий: Ay = y п -Y< 0,02.

Исследуем поведение решения в докритической области. Будем менять y с шагом 1/1000 и используем дополнительную информацию с предыдущего шага. Оказывается, каждому значению параметра у соответствует два решения, причем оба имеют положительное число Re и различаются только амплитудой. С уменьшением y амплитуды постепенно сближаются, и при y = Y n - Ay решения сливаются в одно. Если посмотреть на эти решения с точки зрения изменения амплитуды, то можно увидеть следующую картину: от линии бифуркации в докритическую область ответвляется решение с малой амплитудой. До какого-то значения амплитуды оно существует в докритической области, а затем пересекает линию бифуркации и при дальнейшем росте амплитуды находится в закритической области, то есть при y ^е ( y _п , 2 п ) , и является вторым решением, порожденным пройденной линией бифуркации. Первым решением при этом считаем то, которое сразу от линии бифуркации ответвляется в закритическую область. Таким образом, в докритической области в малой окрестности точки бифуркации каждому значению параметра y е [ Y n - Ay , Y _п ] отвечают два решения, соответствующие случаю источника в начале координат. Два решения, имеющие Re <  0 , существуют всюду в закритической области.

Обратимся теперь к изучению свойств решения задачи А1 при ц ^ 0. Напомним, что для осуществления численного решения необходимо знать вспомогательное значение искомой функции на границе ^ = Y ■ Аналитически показано, что при п = 1 на линии Y 1 = ( ц ² + 1 ) п/4 возникают решения вида (6). Это позволяет задать для функции и ( £ ) вспомогательное значение u ( y ) ■

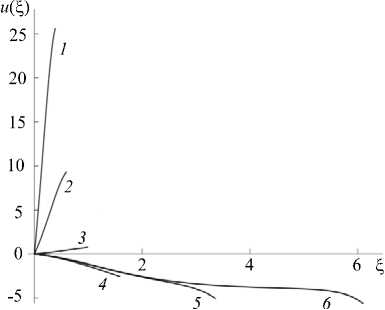
Рис. 1. Эволюция решений при ц = 0,6 , существующих на первой линии бифуркации при различных y : 0,3 (кривая 1 ); 0,5 ( 2 ); 1,0 ( 3 ); 1,6 ( 4 ); 3,4 ( 5 ); 6,1 ( 6 ); критическое значение Y j » 1,06

При численном исследовании обнаружено, что решение, соответствующее Re >  0, существует всюду в докритической области, то есть при у е ( 0, Y 1 ) ; решение, соответствующее Re <  0 , существует всюду в закритической области, то есть при у е ( Y 1 , 2 п ) . Таким образом, линия Y i = ( ц ² + 1 ) п /4 является линией двусторонней бифуркации. На рисунке 1 показана эволюция этого решения при ц = 0,6 и различных значениях параметра у • При заданном ц первая линия бифуркации достигается при у 1 , с точностью до сотых равном 1,06.

На остальных линиях бифуркации при | ц| < 0,2 наблюдается картина, аналогичная той, которая возникает в окрестностях точек бифуркации Y = 3 п/ 4, 5 п/ 4, 7 п/ 4 для случая ц = 0. А именно, от нулевого решения ответвляются два: одно, соответствующее Re <  0 , существует всюду в закритической области, другое ( Re >  0 ) имеет место в малой окрестности линии бифуркации в докритической области, а затем переходит в закритическую область. Причем величина интервала Ay существования решения с положительным числом Рейнольдса зависит

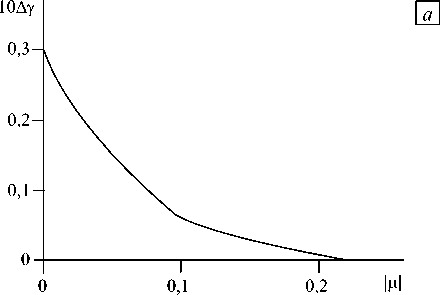
Рис. 2. Зависимость величины интервала существования докритических решений от параметра | ц| для задач А ( а ) и В ( б )

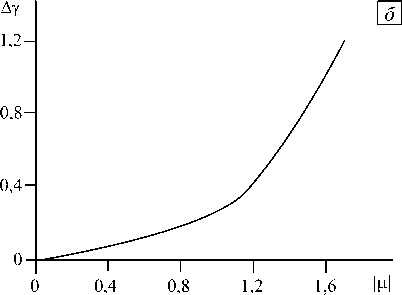
от параметра — ц. Максимального значения интервал Ay достигает при ц = 0. С ростом | ц| величина Ay уменьшается и при | ц| > 0,2 стремится к нулю. Зависимость Ay от | ц| представлена на рисунке 2, а.

При | ц| > 0,2 оба решения, ответвившиеся от линии бифуркации, существуют только в закритической области и соответствуют отрицательным значениям Re .

Таким образом, вся область изменения

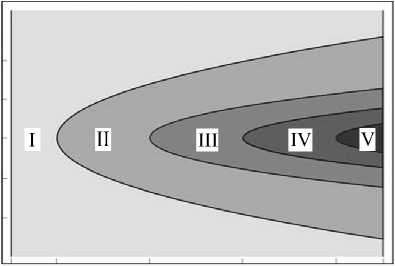
0    л/4 Зл/4 5л/4      7л/4 2л у

Рис. 3. Количество решений задачи течения жидкости между твердой стенкой и свободной поверхностью: I – одно решение с положительным значением Re ; II – одно решение с отрицательным значением Re ; III – три решения; IV – пять решений; V – семь решений

параметров y е ( 0, 2 п ) , -» < ц < +» разбивается

линиями

Y n

ц ² + 1

п

+ п n

( n = 0,1, 2,3)

на пять подобластей (Рис. 3). В I-й подобласти

существует одно ненулевое решение, соответствующее Re >  0. Его эволюция при ц = 0,6 показана на рисунке 1 (кривые 1 - 3 , находящиеся выше оси абсцисс).

Во II-й подобласти, за исключением малой окрестности правой границы, существует решение, соответствующее Re <  0; его эволюцию при ц = 0,6 можно проследить на рисунке 1

(по кривым 4 – 6 , находящимся ниже оси абсцисс).

В III-й подобласти (за исключением малой окрестности правой границы) к последнему решению добавляются два новых, ответвившихся от нулевого решения при переходе второй линии бифуркации y ₂ = 3 ( ц ² + 1 ) п /4 . Вблизи этой линии

они стремятся к решению линеаризованной задачи u =б exp ( 2 ц^/ ( ц ² + 1 ) ) sin ( 3 п^/ ( 2 y ) ) , а с уменьшением | ц| совпадают с точными решениями, найденными при ц = 0 . Аналогичная ситуация повторяется после пересечения каждой линии бифуркации, то есть в IV-й подобласти имеем пять, а в V-й — семь решений.

Решения, существующие во II–V-й подобластях, за исключением малых окрестностей линий бифуркации, соответствуют случаю стока в начале координат, то есть отрицательным значениям параметра Re . Численный анализ этих решений показывает, что наименьшее значение числа Рейнольдса достигается на решении, ответвившемся от первой линии бифуркации, и с точностью до целых равно - 19. Таким образом, для всех закритических решений со стоком в начале координат число Рейнольдса меняется в пределах - 19 <  Re <  0 .

6.    Результаты численного исследования течения жидкости между двумя свободными поверхностями

Численный эксперимент выявил, что все решения задачи В1, найденные в работе [7] при ц = 0 присутствуют и при увеличении | ц|, но величина интервала | ц|, при котором эти решения существуют, различна для разных решений. Так, например, при y = п + 0,2 на интервале | ц| е [ 0; 0,2 ] обнаружено пять ненулевых решений.

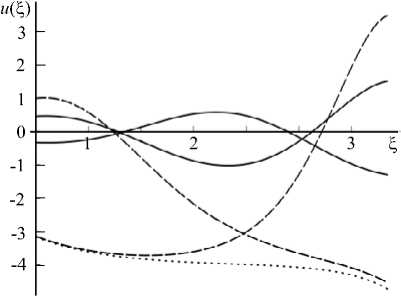
Рис. 4. Пять решений, существующих при ц = 0,2, у = л + 0,2

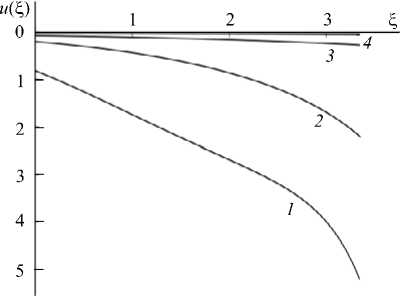
Рис. 5. Эволюция решения с ростом |ц| при y = л + 0,2 и различных ц : 1 (кривая 1 ); 2 ( 2 ); 5 ( 3 ); 10 ( 4 )

Положение решений при ц = 0,2 представлено на рисунке 4: точками изображено решение, полученное из постоянного и = - 4, штриховыми линиями — пара решений, следующих из монотонно возрастающего и монотонно убывающего при ц = 0 решения, сплошной линией — решения на основе немонотонных при ц = 0 функций. При | ц| е [ 0,3; 1 ] из описанных остаются первые три решения, а при | ц| >  1 — только одно решение, которое с ростом | ц| постепенно стремится к тождественно нулевому (Рис. 5).

Сравнение результатов аналитических исследований и численных экспериментов позволяет сделать вывод о том, что все численно найденные решения существуют только до момента достижения соответствующей линии бифуркации (7). Так решения, получающиеся из монотонных при ц = 0 функций, существуют до момента достижения первой линии бифуркации у 1 = ( ц ² + 1 ) п/2 . Решения, которые при ц = 0 имеют два интервала монотонности, существуют до второй линии бифуркации у ₂ = ( ц ² + 1 ) п . Аналогично для третьего типа решений, имеющих три интервала монотонности.

Таким образом, можно предположить, что решения, которые существуют при ц = 0 , в области ц ^ 0 постепенно трансформируются и при приближении к соответствующей линии бифуркации стремятся к решениям линеаризованной задачи, возникающим на данной линии.

Для проверки этой гипотезы сравним решение, полученное при у = л + 0,2, ц = 1 из монотонно убывающей при ц = 0 функции, с решением линеаризованной задачи (8), которое при n = 1 примет вид:

Г 2 ц^ ) Гл^)   Гл^)

и = б exp I —2    I cos I— I cos I— I .

(ц ² + 1 J    ( У J ( у J

Оказывается, расчетные данные для этих решений совпадают с точностью до 2%. Заметим, что значение ц = 1 близко к первой линии бифуркации, которая достигается при

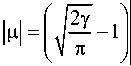
« 1,06.

у=л+ 0,2

Такое же сравнение для решения, полученного из монотонно возрастающей функции, свидетельствует об их существенном различии (см. Рис. 6, а ).

Более подробное исследование в окрестности критического значения (~ | ц| = 1,06) показало, что решение (9) с положительным стремящемся к нулю б существует только в закритической области, то есть при | р| <  1,06, в то время как решение, соответствующее малым отрицательным значениям б , ответвляется в докритическую область. На рисунке 6, б показаны решение (9) с отрицательным б и решение, полученное из монотонно возрастающей при ц = 0 функции при докритическом значении параметра ц = 1,1. Видно, что они близки друг к другу.

Однако в докритической области решение существует на очень малом интервале Ау , величина которого не превосходит 1,2 и зависит от значения ц . Ответвляясь в докритическую область, решение,

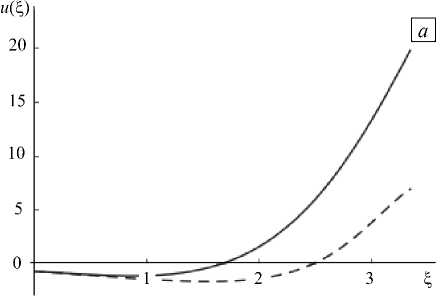
Рис. 6. Закритическое ( а ) и докритическое ( б ) приближение численного решения к решению линеаризованной задачи; сплошная линия – решение линеаризованной задачи, пунктирная линия — численное решение

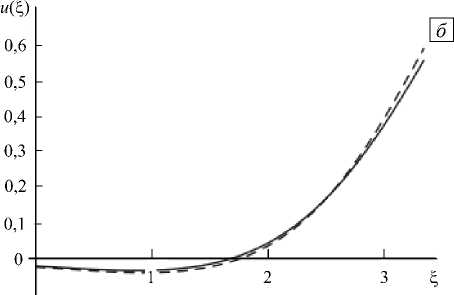
с ростом амплитуды, отходит на максимально возможное расстояние от критического значения параметра у n , а затем вновь возвращается к у n , но уже с большим значением и (0) и существенно изменившись. Этим и объясняется отличие решений на рисунке 6, а . В дальнейшем это решение продолжает существовать в закритической области. Схематическая зависимость значения искомой функции на границе £ = 0 от параметра у при фиксированном значении ц представлена на рисунке 7.

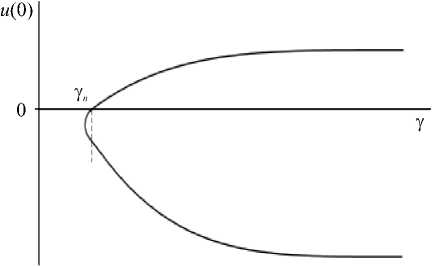
Рис. 7. Схематическая зависимость значения искомой функции на границе ^ = 0 от параметра у при фиксированном значении ц

л/2

л Зл/2 2л

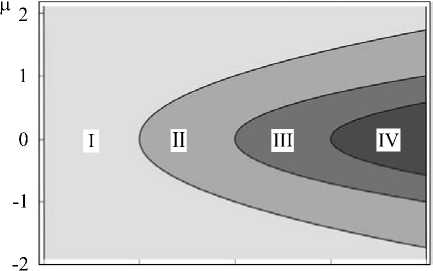
Рис. 8. Количество решений задачи течения жидкости между двумя свободными поверхностями: I – одно решение; II – три решения; III – пять решений; IV – семь решений

Таким образом, и в закритической, и в докритической областях при | ц| >  0,01 имеют место два решения; при | ц| <  0,01 нет решения с положительным числом Рейнольдса. С увеличением | ц| такие решения возникают, причем интервал их существования Ау увеличивается с ростом | ц| . На рисунке 2, б показана зависимость Ау от | ц| для первой линии бифуркации.

Еще раз подчеркнем, что все решения существуют в докритической области при условии источника в начале координат, то есть в случае Re >  0. Для решений в закритической области Re <  0, что означает наличие стока в начале координат.

Абсолютно аналогичная картина наблюдается в окрестности второй и третьей линий бифуркации. В итоге, без учета особенностей в малых окрестностях линий бифуркации, вся область изменения параметров у е ( 0, 2 л ) , -го < ц < +го разбивается линиями бифуркации на четыре подобласти (Рис. 8). В I-й из них существует одно ненулевое решение, полученное из решения и = - 4 при ц = 0 и сходящееся к нулевому решению с ростом | ц| (Рис. 5). Во II-й подобласти к описанному решению добавляются два новых, которые ответвляются от нулевого решения при переходе первой линии бифуркации; вблизи этой линии они стремятся к решению линеаризованной задачи (9), а с уменьшением | ц| совпадают с точными решениями, найденными при ц = 0. Ситуация повторяется после пересечения каждой линии бифуркации, то есть в III-й подобласти имеем пять, а в IV-й — семь решений.

В работе [7] проведена теоретическая оценка числа Рейнольдса, при котором существует решение задачи В, а именно I ReI ≤ Re ^∗ ≈ 54,84 . При численных исследованиях обнаружено, что наименьшее значение параметра Re достигается на решении, возникающем из постоянного при µ= 0 решения u = - 4 , и с точностью до десятых равно: Re = –19, 6 . Все докритические решения, имеющиеся в этой задаче, малы, и соответствующие им значения чисел Рейнольдса не превосходят 0,6. Таким образом, численно найденные решения задачи В существуют при - 19, 6 ≤ Re ≤ 0,6.

Работа выполнена при финансовой поддержке РФФИ (проект № 13-01-00526-а).