Численное исследование эволюции медленного течения неоднородной жидкости на больших временах

В настоящее время для описания эволюции сложных течений вязкой жидкости, имеющих существенно отличающиеся пространственные и временные масштабы, широко практикуются так называемые комплексные (совместные) модели (“coupling models” в англоязычной литературе), соединяющие в себе упрощенные уравнения в погранслойном приближении и более общие уравнения вязкой жидкости [1]. Для численного решения систем эволюционных уравнений, составляющих модель, применяются традиционные методы (например, метод Рунге-Кутты), в которых используются разномасштабные по времени сетки, и, при возможности, осуществляется расщепление по физическим процессам [2].

Характерной особенностью рассматриваемых течений является наличие различных режимов эволюции: резкие изменения скоростей на относительно малом интервале, в так называемом «временнóм пограничном слое», и медленная стадия, когда за длительный промежуток времени происходят незначительные изменения. В этом случае система уравнений, моделирующая процесс, оказывается жесткой, и при ее численном решении обычными методами возникают существенные ограничения, а именно, шаг интегрирования по времени должен оставаться малым на всем протяжении счета. Попытки уменьшить время вычисления на медленной фазе путем увеличения шага интегрирования приводят к резкому возрастанию погрешности и вообще к потере устойчивости вычислительного процесса. Таким образом, возникает необходимость создания численных методов, которые обеспечивали бы правильное поведение решения в «пограничном слое», а также возможно точнее воспроизводили бы его на участке интегрирования за пределами этого слоя. В настоящее время специальные численные методы решения жестких систем разработаны только для обыкновенных дифференциальных уравнений [3]. Однако применение таких методов для моделирования рассматриваемых сложных течений сопряжено со значительным ростом вычислительных затрат [4].

При использовании общих методов численного решения нестационарных систем уравнений гидродинамики [5] малый шаг дискретизации по времени еще не гарантирует хорошую вычислительную точность. Как показано в работе [6], при постановке естественных условий непрерывности поля скоростей и напряжений на границе сопряжения разнородных уравнений на больших временах поле скоростей определяется с большой погрешностью.

Однако при численном моделировании в некоторых практических приложениях (например, в тектонике и геофизике) поведение решения во «временнóм пограничном слое» не играет существенной роли, а гораздо более важным является изучение особенностей течения на медленной фазе. Поэтому важное значение приобретает разработка численных алгоритмов, которые позволяли бы достаточно точно моделировать решение на больших временах и производить расчет с большим шагом по времени для сокращения чрезмерных вычислительных затрат.

В настоящей работе построена комплексная численная модель, в которой для описания течения в толстом однородном слое применяются уравнения Стокса, а в тонком многослойном пласте — уравнения Рейнольдса. Методом асимптотических разложений получено уравнение, связывающее смещения границ слоев многослойного пласта со скоростями на его нижней границе. С помощью этого уравнения, как дополнительного условия, построена система квазилинейных параболических уравнений, представляющая эволюцию течения на больших временах. Найдено аналитическое решение, и исследуется характер течения в приповерхностной области на малых и больших временах. Проводится сравнение численного и аналитического решений. Показан пример возможного приложения модельных результатов в тектонике и геофизике.

2.    Система уравнений

Пусть расчетная область представляет собой относительно толстый слой однородной вязкой несжимаемой жидкости, на поверхности которого расположен тонкий пласт, состоящий из N вязких слоев. Обозначим через Z_k , где к = 0, N , границы многослойного пласта. Задаются скорости движения жидкости на нижней границе расчетной области.

Для описания движения вязкой несжимаемой жидкости в поле силы тяжести применяем следующие уравнения:

u ltt + u 1 u 1,1 + u 2 u 1,2 = - p ,1 + ^U i ( u 1,11 + u 1,22 ) , u 2, t + u l u 2,1 + u 2 u 2,2 = - p ,2 + ^U i ( u 2,11 ⁺ u 2,22 ) -^P i g ,

где p i и u i — плотности и вязкости слоев (постоянные внутри слоев); u_k — компоненты скорости; p — давление; g — ускорение силы тяжести; нижний индекс « , t » обозначает частную производную функции по времени, а « , k » — частную производную функции по координате x_k . Поле скоростей также должно удовлетворять уравнению неразрывности:

u 1,1 ⁺ u 2,2   ^0.

Приведем уравнения к безразмерному виду:

Х1 = Lx’,   x2 = Lx2,   ц,.=Цо H2,   Pi=Po P‘,   U1 = uо u‘,   u2 = u0 u2,   P = P0 P', где L , u0 , p0 , p0 =p0gL и 10 = L/u0 — это, соответственно, масштабы длины, вязкости, плотности, давления, скорости и времени (в дальнейшем, для удобства, штрихи опускаются).

Вязкие течения в земной коре и мантии являются медленными с пренебрежимо малым числом Рейнольдса [1, 7], поэтому в уравнениях (1) инерционными и конвективными членами пренебрегаем.

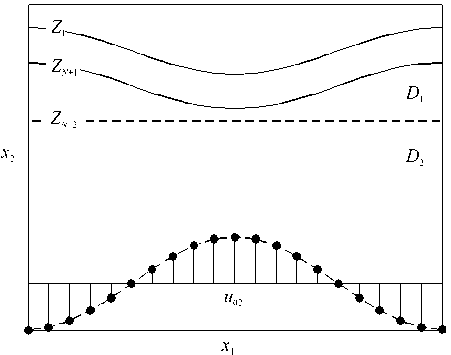
Рис. 1. Общая схема расчетной области: сплошные линии – границы вязкого пласта, штриховая линия – фиктивная граница; отрезки с маркерами изображают эпюру скорости движения нижней границы

Так как горизонтальный размер многослойного пласта существенно больше вертикального и горизонтальные скорости течения в нем значительно больше вертикальных, для описания движения жидкости можно применить упрощенные уравнения вязкой жидкости в длинноволновом приближении (уравнения Рейнольдса) [4]. Однако течение жидкости имеет субгоризонтальный характер не только в самом пласте, но и в окрестности верхней границы подстилающего его вязкого слоя. Поэтому поставим ниже границы Z_N + 1 (на расстоянии порядка толщины пласта) фиктивную горизонтальную границу Z_{N + 2},

в длинноволновом приближении получим из (1)

которая разделит расчетную область на верхнюю — D ₁ , и нижнюю — D ₂ , подобласти (см. общую схему на Рис. 1).

Упрощенные уравнения вязкой жидкости при следующих предположениях: характерный

горизонтальный масштаб возмущений много больше вертикального; негидростатические напряжения существенно меньше гидростатического давления; плотность не убывает с глубиной:

p ,1 f   ^Ц , ^u 1,22 ,

Р ,2 = ^-Р /  ⁽ i = 1, ^{N +} 1, f = P o g^K^ u 0 )),

В (3) поле скоростей удовлетворяет уравнению неразрывности (2) и следующим граничным условиям:

p = 0,     Ц 1 u 12 = 0,     z = Z 1 ,

[ u ]-= 0,    [ p ]-= 0,    [Ц1 Ui2 ]-= 0, z = Z,    (i = 1, N + 2).

Кроме этого на подвижных границах раздела пласта заданы кинематические условия отсутствия перетока массы u2 (x1,Z,,t)-Z^u2 (x1,Z,,t)-Z. t = 0    (, = 1,N +1)(5)

и начальное положение границ слоев пласта

Z,( x1,0) = Zi0    (i = 1, N +1).(6)

Используя уравнение неразрывности (2), преобразуем условие (5) следующим образом:

Z,, t =- S (X1, Z,),1 -(U1 (X1, ZN+2)(Z,-Zn+2 ))д + u 2 ( X1, Zn+2 )    (i = 1Л+1).(7)

x ₂

где     S ( x 1 , x ₂ ) = J ( u 1 ( x 1 , z ) - u 1 ( x 1 , Z_{N + 2} ) ) dz    ( , = 1, N + 1).

Z N + 2

На боковых границах области D ₁ также поставим условия отсутствия перетока массы:

Z^ = 0.(8)

Решая уравнения (3) с учетом условий (4), определим значения u ₁ , u ₂ и p на границах слоев. После подстановки их в (7) и некоторых преобразований получим уравнения относительно границ слоев Z :

/ (             N+1                           AA

( , = 1, N + 1),      (9)

Z,t = I I 41 Z 1,1 + E Ak (pk — Рk-1 )Zk,1 I - u1 (x1, ZN+2 ) (Z, — ZN+2 ) I  + u2 ( x1, ZN+2

l\            k =2                         У                                    )1

где A, = A j = f N ^ h ^ h^—    h^k     ( i <  j , i , j = 1, N + 1), h , = Z , - Z _M   ( i = 1, N + 1), 5 j — символ

т=т m~j — ц k1+6^+dj

Кронекера.

Таким образом, эволюция поверхности и границ раздела слоев описывается системой нелинейных уравнений параболического типа (9) с граничными условиями (6), (8).

Для моделирования течения в подобласти D ₂ воспользуемся уравнениями (1) без инерционных и конвективных членов (уравнениями Стокса):

- p ,1 f + ^ц N + 1 ⁽ u y1 + ^u 1,22 ) = 0,

• - p ,2 ^{f + Ц} N + 1 ⁽ u 2,11 ⁺ u 2,22 ) -^P N + 1 ^f = ^0.

Поле скоростей из (10) также удовлетворяет уравнению неразрывности (2).

На боковых границах расчетной области зададим условия гладкой неподвижной стенки

• ^u 1 = 0,      ^ц N + 1 ^{( u} 1,2 ⁺ u 2,1 ) = ⁰ ,

а на нижней границе — скорости

U 1 = u ₀₁,     U 2 = u ₀₂.

Исходя из (4), условия сопряжения па границе z = Z_{N + 2} приобретают следующий вид: ц N + 1 ( U 1,2 + U 2,1 )1     =- f Y I* Z ,1 + Y ( p k -P k - 1 ) Z k ,1| Z - Z , + 1 ) ,

¹ Z N + ²            - = 1 <             k = 2                         )

N

• - p + 2ц N+1 U 2,2    =- f Yp(Z- - Z,+1 У

• ' ZN+2            ,=1
3.    Аналитическое исследование

Для аналитического исследования выберем модель с однослойным пластом, характеризуемую следующими масштабами и значениями безразмерных параметров:

• - L = 400 км; p ₀ = 3000 кг/м^3; g = 9,81 м/с²; ц ₀ = 10 ²² Па^с; u ₀ = 0,01 м/год ® 3,17 - 10 ^{- 10} м/с [7] (тогда 1 ₀ = 4 ■ 10 ⁷ лет « 1,26 ■ 10 ¹⁵ с, f « 494,989);

• -    положения границ в начальный момент времени Z 1 = 1, Z ₂ = 0,9;

• -    плотности слоев р 1 = 1, р ₂ = 1,1;

• -    вязкости слоев ц 1 = 1, ц ₂ = 1;

• -    скорости на нижней границе и ₀₁ = 0 , u ₀₂ = - 0,002cos x 1 .

С помощью преобразования Фурье по x ₁ и преобразования Лапласа по t получим аналитическое решение при малых возмущениях границ слоев [8].

U 1 = ^w 0 ( ( A1exp ( -^ i t ) + S ₁₂exp ( -X ₂ 1 ) ) + B₁₃ ) sin x 1 , U 2 = ^w 0 ( ( B ₂₁exp ( -^ 1 1 ) + B ₂₂exp ( -^ ₂ 1 ) ) + B ₂₃ ) cos x 1 ,

где коэффициенты X , >  0 и B j вычисляются через толщины слоев, вязкости и плотности, причем Х 1 » Х ₂. Отклонения границ слоев от начального положения найдем по формулам:

^ Zi = ^к I Е B j (1 - exP ( -Xy t ) + B 3) I cos X ( i = 1,2). -       0 , j _1 x                      j,      - 3₇ )         ¹

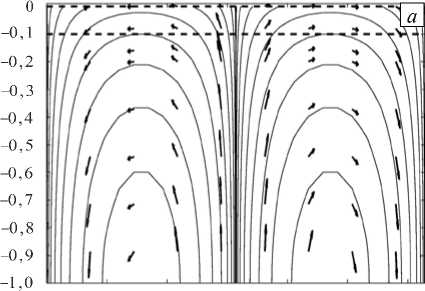
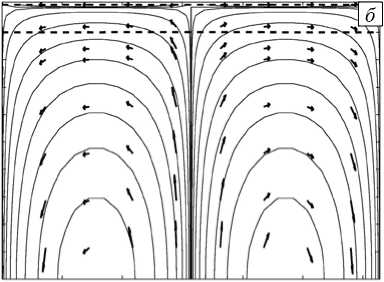
Как видно из результатов, представленных на рисунке 2, на начальной стадии (при t = 0,01) границы Z 1 и Z ₂ смещаются в одном направлении, а на больших временах (при t = 4 ) они движутся противоположно друг другу. На рисунке 3 показаны соответствующие этим смещениям поля скоростей. Для их наглядного представления используется функция тока, которая определяется из (7) . Сопоставление рисунков 3 а и 3 б показывает, что существенное изменение поля скоростей происходит только в небольшой окрестности верхней границы Z ₁ , а в нижней части расчетной области течение почти стационарное.

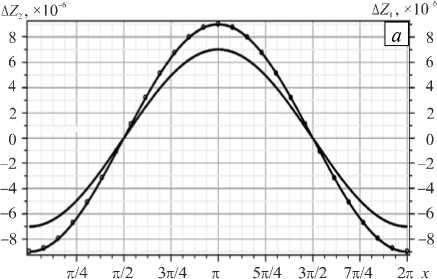
Рис. 2. Смещение границ слоев на малых и больших временах t : 0,01

( а ) и 4 ( б ); сплошные линии – граница Z ₁ , линии

с маркерами – граница Z ₂

0       1       2        3       4       5        6

A',

о

-0.1

-0,2

-0,3

-0,4

-0,5

-0,6

-0,7

-0,8

-0,9

-1,0

0       1       2        3       4       5        6

Рис. 3. Изолинии функции тока (сплошные линии) на малых и больших временах t : 0,01 ( а ) и 4 ( б ); стрелками показаны направления вектора скорости, штриховыми линиями – границы слоев

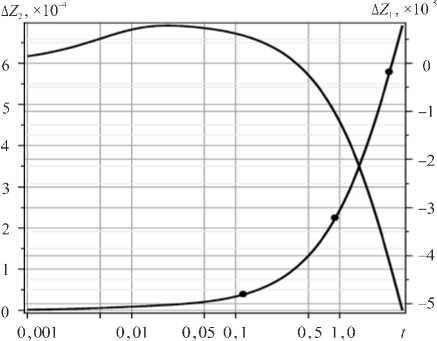
Рис. 4. Смещения границ в точке х 1 = п относительно начального положения на малых и больших временах: сплошная линия – смещение границы Z ₁ , сплошная линия с маркерами – смещение границы Z ₂

На рисунке 4 показана эволюция смещений границ относительно начального положения в точке х 1 = п , где их величины максимальны. Для того чтобы наглядно изобразить на одном графике эволюцию движения границ полностью, по оси времени использовался логарифмический масштаб (то есть деления на оси t соответствуют значениям lg t ). По результатам видно, что характерной особенностью эволюции течения является наличие двух различных режимов: подъем обеих границ Z ₁ и Z ₂ за относительно короткий начальный промежуток (за так называемый «временнóй пограничный слой»), переходящий в медленную стадию, на которой происходят нисходящее движение верхней границы Z ₁ и восходящее движение границы Z ₂ .

4.    Численная модель

Численное решение находилось следующим образом. Исходя из положения поверхности и границ слоев в начальный момент времени, методом конечных элементов вычислялось поле скоростей в нижней подобласти D ₂ с помощью уравнений (2), (10) и граничных условий (11)-(13). Использовалась вариационная формулировка уравнений (2), (10). Для этого (10) скалярно умножались на соленоидальное поле v_i и преобразовывались по формуле Ocтроградского–Гаусса с учетом граничных условий (12). Получалось следующее вариационное уравнение:

J (u, v) = C (Ui, Vi) - F( Vi) - F,( Vi) = 0,(16)

где

C ( U , V i ) = jj ^ ( Uy + U j,i )(Vi, j + V j , i ) dx    ( i = 1, 2),

D

F(^ = —jjPgV2 dx’

D

N +1              kN

F2(Vi) = - j ЕЬ Z.,j+Z(P 1 -P1 -1)Z,j l(Zk -Zk+1)V1 dГ- j Ipk (Zk -Zk+1)V2 dE 7 k=1 x            1=2                     /

Z N + 2                                                                            Z N + 2

Для численного решения (16), (17) применялся модифицированный метод конечных элементов в сочетании с методом проекции градиента (подробное описание метода решения приводится в работе [6]). Затем по известным значениям скоростей на границе сопряжения Z N _{+ 2} определялось поле скоростей в верхней подобласти D 1 . После этого устанавливались положения границ слоев на следующем временном слое путем решения системы разностных уравнений, приведенной ниже.

Обозначим x l ( 1 = 1, L ) и t™ ( m = 1, M ) — равномерные расчетные сетки для координаты х 1 и времени t . Тогда неявная схема для уравнений (9) с граничными условиями (8) примет следующий вид [5]:

г 1 , m + 1         1 , m

'i     - Z i

A t

1 Л A^ , m + 1 । A + 1, m + 1

A x 1 (       2

' I + 1, m + 1    y 1 , m + 1

' 1        - Z 1

A x 1

1 I - 1, m + 1        1 , m + 1 r,l , m + 1     ^1 - 1, m + 1

i 1     ⁺ A n    ^Z 1     - ^Z 1

A x 1

N + 1

+I(P k

k = 2

P k-1)

1 1 , m + 1 ik

1 + 1, m + 1 + A ik

' 1 + 1, m + 1     y 1 , m + 1

' k - Z k

A x 1

2             A x 1

1 + 1, m u 1

( Z + 1, m + 1

' 1 + 1, m + 1 ' N + 2

) ^{- u1,1}

( Z * ⁴- ^{m + 1}

у 1 - 1, m + 1 \ ^

Z N + ² )

+ U 2,

( i = 1, N + 1,   1 = 2, L - 1),

где Zi '^{, m} , и^ ^m и u^ ^{, m} — значения сеточных функций, аппроксимирующих, соответственно, Zi , u 1 и u ₂ в узлах ( x^l_vt ^m ) ; A ikm = A_ik |_z=_{z 1m} ; A x 1 и A t — шаги расчетных сеток по x 1 и t . Значения сеточных функций в фиктивных узлах x ^ ( 1 = 0, L + 1) дополнялись следующим образом:

Z0,m       2,m    . 0,m . 2,m     . 0,m . 2,m i = Zi  ,  U1   =- U1  , U 2 = U 2 ,

Z iL ^{+ 1}, ^m = z iL - *> ^m ,   U L ^{+ 1}, ^m =- U L " *’ ^m ,   u L ^{+ 1}, ^m = u ₂ L " *’ ^m   ( m = ik M ).

Так как система уравнений (18) нелинейна относительно Z * , ^{m + 1} , для нахождения ее решения использовался метод итераций. В качестве начальных приближений для коэффициентов A ik^{m + 1} принимались их значения на предыдущем шаге по времени — A ik^m , которые подставлялись в (18), и из решения полученной линеаризованной системы определялось новое приближение для Z’i , ^{m + 1} . По этим

аналитическое решение, штриховая линия — численное решение

Далее повторялась вся процедура.

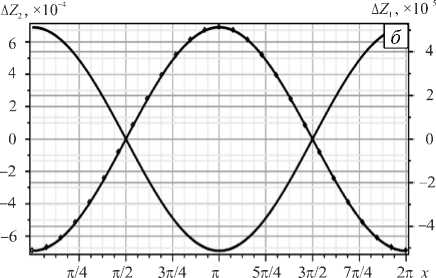
Проведено сравнение результатов численного решения при малых отклонениях границ слоев от начального положения с аналитическими (14), (15). На рисунке 5 представлены смещения границ слоев относительно их начального положения в точке х 1 = п , где погрешность решения максимальная. Численная схема построена на равномерной по координатам расчетной сетке с шагами А х 1 = 2п/ 14 и А х ₂ = 0,1 . Шаг по времени А t задавался равным 0,005. Дальнейшее увеличение А t приводило к значительным искажениям данных численного расчета. Таким образом, на реализацию эволюционной задачи до момента времени t = 4 потребовалось 800 итераций. Относительные погрешности решения на границах слоев составили: n ( Z 1 ) ~ 16,2% и n ( Z ₂ ) ~ 13%.

На рисунке 6 а показаны изолинии функции тока, полученной из численного расчета в момент времени t = 4. Относительная погрешность для функции тока примерно равна п ( S ) ® 3,4%. Однако, если численные значения смещения границ Z_i заменялись на их значения из точного аналитического решения, то погрешность резко возрастала: n ( S ) ~ 123 % (см. Рис. 6 б) . Таким образом, численное решение оказалось очень чувствительным к незначительным возмущениям границ слоев, а также к величине шага по времени, уменьшение которой приводило к значительному увеличению времени счета.

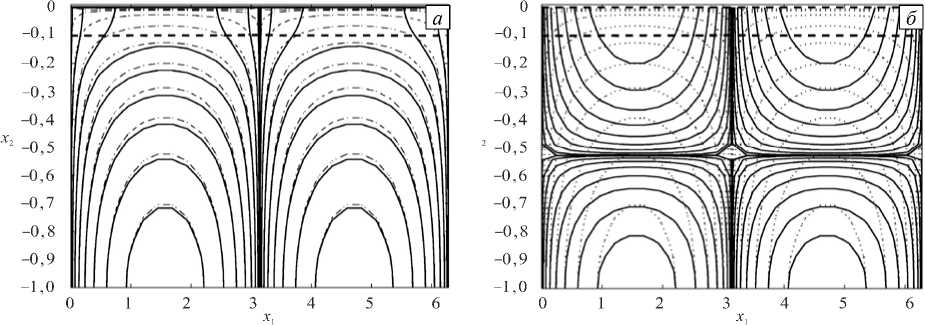
Рис. 6. Изолинии функции тока при t = 4, построенные для различных вариантов выбора Z , .: ( а ) - Z,. взяты из численного решения; ( б ) - Z_i взяты из точного решения; штриховыми линиями обозначены границы слоев, сплошными линиями – изолинии функции тока, полученные из численного решения уравнений (18); тонкими штрихпунктирными линиями для сравнения показаны линии тока точного решения

При численном решении подобных жестких эволюционных задач основная проблема заключается в том, чтобы обеспечить качественно правильное поведение численного решения как на участке «временнóго пограничного слоя», так и возможно точнее воспроизвести решение на основном участке интегрирования, вне этого слоя [4]. В некоторых приложениях, например, в тектонике и геофизике, поведение решения во «временнóм пограничном слое» практически непредсказуемо, так как нет информации ни о моменте начала процесса, ни о начальных условиях. В связи с этим, более важное для исследователя значение имеет поведение течения в промежутке времени, отвечающем медленной фазе, слабо зависящей от начальных условий. Поэтому возникает необходимость разработки численного метода, который позволил бы достаточно точно моделировать решение на больших временах. При этом желательно вести счет с большим шагом по времени, поскольку малый шаг при моделировании медленно меняющегося процесса приводит к неоправданному увеличению вычислительных затрат. Однако при использовании методов, не учитывающих указанные особенности процесса, несмотря на медленное изменение численного решения, шаг интегрирования должен оставаться малым. Попытки уменьшить время вычисления за счет ув еличения шага интегрирования приводят к резкому возрастанию погрешности и к значительным искажениям численного решения.

5.    Асимптотическое условие на границе сопряжения

Так как плотность в коре и мантии Земли изменяется в пределах 3000–3300 кг/м³, величину s = max ( р k -р k - 1 ) можно считать малым параметром. Представим решение системы (9) в виде сумм:

Z 1 = Z 1 ( Х 1 , t ) + ^ 1 ( Х 1 , т ) , Z 2 = z 2 ( Х 1 , t ) + ^ 2 ( Х 1 , т ) ,

где с и с2 являются пограничными функциями, компенсирующими невязки начальных условий и быстро убывающими к нулю на бесконечности, т — tjб — «быстрое» время [9]. Очевидно, что начальные условия для zt и сi из (19) должны удовлетворять следующим соотношениям: Zi (x1,0) — zi (л:1,0) + сi (л',,0) .

Предположим, что скорости на границе сопряжения подобластей являются малыми величинами:

U 1 ( Хр Z n + 2 ) — Б U 1 ,

u 2 ⁽ x 1 , ^Z n + 2 )   ^{Б U} 2 .

Для того чтобы выделить из решения функции с i , разобьем систему, полученную в результате подстановки (19) в (9), следующим образом [10]:

Г                 N+1

^Б zi , т ^— I A i 1 |_z = z ^z 1,1 ^{+ Б} 5 AiAz, = z ^Y k z k ,1 I ^{— Б U} 1 ⁽ zi ^{- Z} 3 ) ,1 + ^{Б U} 2 ,

V                    k=2       ' */1

I            N+1           AI           N+1

• с i, t — I Ai1 zi — zi Z 1,1 +Б^ Aik|z,= zi Y kZ k ,1 I -I Ai1 iz,=zi z1,1 +Б^ A-iAz,— zi Y kzk ,1 I - БU1 ( Zi — zi)

V                     k=2                    7,1 V                    k=2

где Y k = ( P k - P k - 1 )/^Б .

Представим приближенное решение в виде асимптотических разложений:

z i = z i0 +Б z i 1 + ..., C i =C ,0 +БС 1 + ....

Подробный асимптотический анализ уравнений приводится в [11].

Подставив (21) в (20) и приравняв коэффициенты при одинаковых степенях б , получим следующие уравнения в первом приближении: - уравнение относительно z _n:

Г                n+1

0 -I Ai1 Iz,— zi0 z11,1 + 5 Aiklzi- zi0 Y kzk 0,1 I -U1 (-ZN+2 ),1 + U2.(22)

V                    k=2

- система уравнений относительно z ₀ :

zi0,T=| Ai1 lz, = z,/11,1 +5+1 Aik\z, = z„ Ykzk0,1 I -(U1 (zi0 -Zn+2))1 + U2.(23)

V                       k=2                        7,1,

Таким образом, в первом приближении, на больших временах, смещения границ слоев связаны со скоростями на границе Z_{N +2} обыкновенным дифференциальным уравнением (22) и не зависят от начального рельефа поверхности и границ раздела слоев.

Система уравнений (23) описывает эволюцию границ пласта на больших временах. Для ее решения использовалась численная схема, аналогичная (18):

l , m + 1       l , m        i (  а 1 , m + 1  .    а 1 + 1, m + 1     l + 1, m + 1        l , m + 1        a I - 1, m + 1  .    a I , m + 1     l , m + 1       l - 1, m + 1

• ^z i 0    ^{- z} i 0  _  ¹ I ^A i 10    ^{+ A} i 10      ^z 11      ^{- z} 11       ^A i 10     ^{+ A} i 10    ^z 11    ^{- z} 11

  --------—-------

• At       Ax 1 V 2            Ax1              2            Ax1

—

N + 1 + 5 y k k — 2

U l ^{+ 1, m} ( z i

. l + 1, m + 1

' i 0

a l , m + 1 ,     aI + 1, m + 1

A ik 0   + ^A ik 0

_ l + 1, m + 1     „I , m + 1

z k 0 _______ z k 0

A x ₁

< l - 1, m + 1 ,    aI , m + 1    l , m + 1    l - 1, m + 1

¹ik 0     + ^A k 0   z k 0    - z k 0

2            A x 1

—

Z l + 1, m + 1 \ т t I - 1, m /  l - 1, m + 1

N + 2 ) ^{- U} 1  ^,   ( z i 0

—

ry l - 1, m + 1 \

^Zn + ²   )

+ и 2^{, m}

( i — 2, N + 1, l — 2, L - 1),

где z i ⁰, ^m — z i ², ^m , U 1⁰, ^m — - U ², ^m , U 0 ^m — U ₂², ^m ; z iL ^{+ 1}, ^m — z iL ^{- 1}, ^m , U L ^{+ 1}, ^m — - U L ^{- 1}, ^m , U L ^{+ 1}, ^m — U L ^{- 1}, ^m ( m — 1, M ); z i^l 0 ^m , U l ^{, m} и U 2^{, m} — значения сеточных функций, аппроксимирующих, соответственно, z i ₀ , U 1 и U ₂ в узлах ⁽ x^ t ^m ); A lkm ^— A ik Lz 'm .

• ^{1    z}i - z i 0

Проведено сравнение численного решения с применением асимптотического условия (22) для малых отклонений границ слоев от начального положения с предыдущим вариантом. Рисунок 7 позволяет проследить эволюцию смещений границ слоев из численного решения (23) в точке x 1 — п относительно их

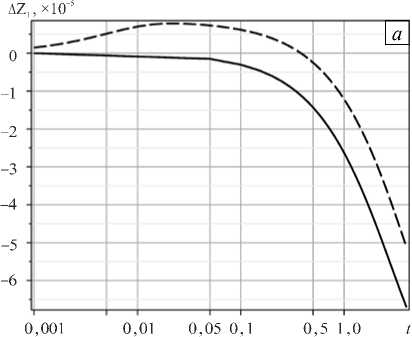
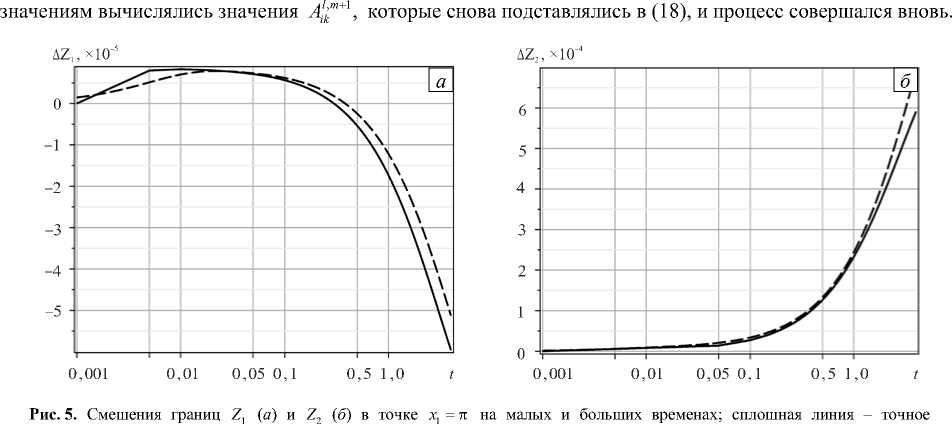
Рис. 7. Смешения границ Z 1 ( а ) и Z 2 ( б ) в точке х 1 = п на малых и больших временах: сплошная линия - точное аналитическое решение, штриховая линия – численное решение с применением асимптотического условия (22); П ( Z 1 ) « 0,3073 , n ( Z ₂ ) ” 0,1462

начального положения и сопоставить с аналитическим решением. При шаге по времени A t = 0,2 на решение эволюционной задачи до момента t = 4 потребовалось 20 итераций по времени. Погрешность численного решения для границ слоев получилась равной n ( Z 1 ) ~ 30,7 % и n ( Z ₂ ) ~ 14,6 %.

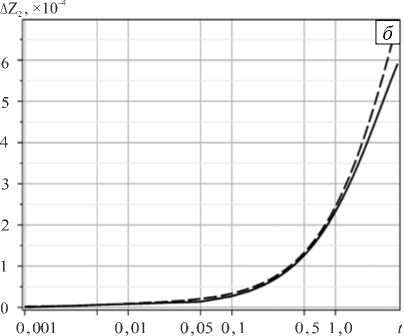
На рисунке 8 приведены изолинии функции тока, соответствующие моменту времени t = 4. Погрешность численного решения для функции тока получилась равной n ( S ) ~ 3,6%, а при задании смещения границ из аналитического решения — n ( S ) ~ 4,29%. При сопоставлении результатов на рисунках 6 а и 8 а видно, что они идентичны. Хотя погрешность смещения границы Z ₁ и была почти вдвое большей по сравнению с предыдущим вариантом, у функции тока она сохранила тот же порядок величины. Сравнение же рисунков 6 б и 8 б показывает значительную разницу: в отличие от предыдущего варианта, погрешность функции тока практически не изменилась при замене смещений границ на их значения из аналитического решения. Таким образом, с помощью асимптотического условия (22) без существенных ограничений на шаг по времени получено численное решение эволюционной задачи (23), устойчивое к возмущениям границ слоев и имеющее хорошую точность.

Проведено численное исследование течения в расчетной области с двухслойным пластом на развитой стадии при больших отклонениях границ слоев от начального положения. Результаты представлены на рисунке 9. Так как скорость течения в нижней подобласти в процессе эволюции почти не меняется, изолинии функции тока показаны только для верхней части D 1 . При t = 5 изменения происходят лишь в окрестности верхней границы Z 1 , а затем при t = 10 поля скоростей разделяются на две зоны, в которых направления вертикальных смещений прямо противоположны. Верхняя зона охватывает почти весь

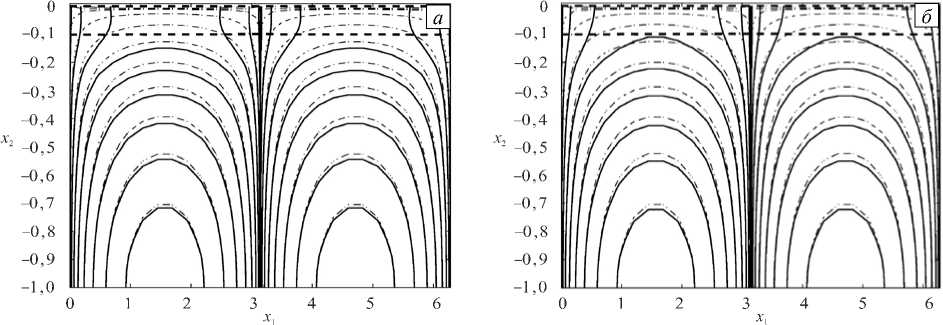
Рис. 8. Изолинии функции тока при t = 4 , построенные с применением асимптотического условия (22) для различных вариантов выбора Z_i : ( а ) - Z_i взяты из численного решения; ( б ) - Z_i взяты из точного решения; штриховыми линиями обозначены границы слоев, сплошными линиями – изолинии функции тока, полученные из численного решения уравнений (24); штрихпунктирные линии – линии тока точного решения

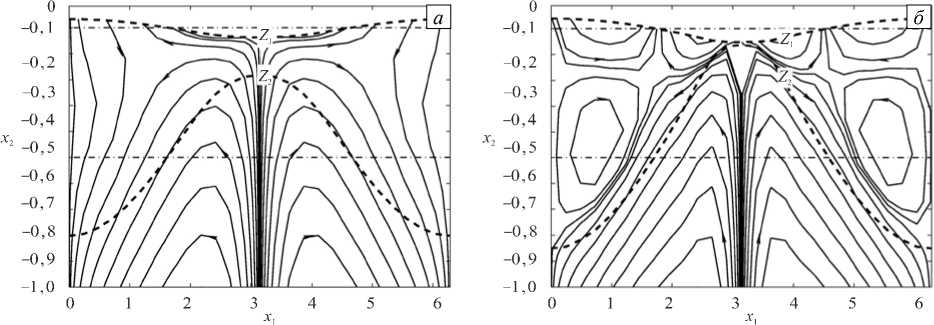
Рис. 9. Профили больших отклонений границ слоев от начального положения и изолинии функция тока в верхней части расчетной области, вычисленные с применением асимптотического условия в различные моменты времени t : 5 ( а ); 10 ( б ); сплошные линии со стрелками – линии тока течения, штриховые линии – границы слоев, штрихпунктирные линии – начальные положения границ слоев

верхний слой, заключенный между границами Z1 и Z2 . Здесь наблюдается довольно сложная картина с образованием замкнутых ячеек по обе стороны от места поднятия границы Z2 .

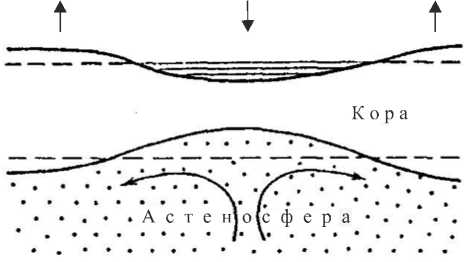
Рис. 10. Эрозия нижней части земной коры конвективными течениями в мантии (рисунок взят из [12])

– наличие малого параметра в уравнениях (9) приводило

решения достигалась только при очень

малых шагах

Таким образом, применение асимптотического уравнения (22) в качестве дополнительного ограничения на искомое решение позволило существенно сократить вычислительные затраты, и достигалось это следующим путем:

– поле скоростей на больших временах вычислялось с хорошей точностью за одну итерацию. При использовании обычного способа сопряжения разнородных уравнений по скоростям и напряжениям поле скоростей имело очень большую погрешность (см. Рис. 6). В этом случае потребовались бы дополнительные уточняющие итерации для получения приемлемой точности, что значительно увеличивало бы время счета;

к тому, что приемлемая точность численного по времени. Преобразование эволюционных

уравнений с помощью асимптотического

уравнения (22) позволило вычленить из решения быстро

убывающую компоненту («временнóй пограничный слой») и достигнуть хорошей точности численного решения на медленной стадии даже при задании большого шага дискретизации по времени.

Как показано на рисунках 6, 8, для реализации одного и того же решения при обычном методе использовался шаг по времени 0,005, и потребовалось совершить 800 шагов, а асимптотическое условие (22) позволило увеличить шаг по времени до 0,2 и получить решение за 20 шагов.

Представленные результаты моделирования могут быть использованы в геофизических приложениях для изучения процесса формирования крупномасштабных тектонических прогибов, которые, по мнению многих ведущих исследователей [12], образовались в результате так называемой подкорковой эрозии, то есть перемещения конвективных течений в астеносфере — в верхнем слое мантии земной коры, из-под прогиба в окружающие области. Общая тектоническая схема этого процесса приведена на рисунке 10.

6. Заключение

На основе уравнений Рейнольдса и Стокса разработана комплексная численная модель, описывающая эволюцию медленного вязкого течения в расчетной области, включающей в себя относительно толстый слой вязкой жидкости и многослойный вязкий пласт на его поверхности.