Численное исследование конвекции расплавленного магния в аппарате восстановления титана

В жидких металлах, обладающих хорошей теплопроводностью, молекулярный перенос тепла, как правило, настолько эффективен, что конвективным теплопереносом при расчете технологических устройств можно пренебречь. Турбулентная конвекция в жидкостях с малым числом Прандтля Pr = v/% (здесь v — кинематическая вязкость , х — температуропроводность) имеет ряд особенностей и активно изучается фундаментальной наукой, хотя экспериментальные исследования связаны с большими сложностями и очень редки (см., например, обзор [1]). Встречаются, однако, ситуации, в которых конвективные течения в металле могут существенно влиять на работу оборудования, и для учета их роли в технологических процессах необходимы либо экспериментальные, либо численные данные. Так, задачи проектирования жидкометаллических систем охлаждения реакторов стимулировали в последнее время развитие вычислительных кодов для расчета турбулентных конвективных течений жидких металлов [2, 3], а также проведение экспериментов по турбулентной конвекции в жидком натрии в протяженных цилиндрах с различной ориентацией относительно силы тяжести [4–7].

Процесс металлотермического восстановления титана является другим примером технологического процесса, в котором термогравитационная конвекция играет важную роль [8, 9]. Реторта для

восстановления титана представляет собой цилиндрический сосуд диаметром до 2 м и высотой до 4 м, в котором находится жидкий магний при температуре 850 ° С. На поверхность магния подается тетрахлорид титана (ТХТ). Химическая реакция протекает преимущественно на поверхности. В результате образуются губчатый титан и двухлористый магний, опускающиеся на дно реторты:

2Mg + TiCl4 = Ti + 2MgCl2 + Q.

Процесс восстановления титана занимает более двух суток и в значительной степени остается «черным ящиком», так как возможности каких-либо измерений во время процесса крайне ограничены (измеряется только температура наружной поверхности реторты в нескольких точках). При этом за счет управления подачей тетрахлорида титана, сливом хлористого магния, охлаждением и нагревом печи необходимо обеспечить устойчивую реакцию. В настоящее время до 5% производственных циклов выбраковываются вследствие нештатных ситуаций, связанных с нарушением процесса осаждения хлористого магния, выходом на поверхность магния титановой губки, локальным перегревом реторты. Основные надежды на контроль за ходом реакции технологи производства титановой губки в течение десятилетий связывали с измерением уровня магния в реакторе, для чего предлагались различные косвенные методы (например [10]). Однако попытки их использования в реальном производстве показали, что они работают только на начальных стадиях реакции, не решая проблему обеспечения устойчивой реакции до завершения цикла. Из обобщения результатов этих работ следует, что контроль реакции не возможен без детального понимания не только химии, но и гидродинамики процесса в реакторе.

Поскольку реакция сопровождается выделением большого количества тепла ( Q = 1707 кДж на 1 кг тетрахлорида титана [11, 12]), радиальный температурный градиент может достигать сотен градусов на метр. Реторта помещается в печь, которая совместно с системой обдува создает тепловой режим реакции. Градиенты температуры вызывают в массиве магния конвективные течения, влияние которых на процесс восстановления титана остается предметом обсуждения специалистов. Именно изменение характера конвективного течения является одной из возможных причин возникновения так называемого «неделения», при котором побочный продукт реакции (соль магния, плотность которой близка к плотности магния) перестает осаждаться на дно реактора и процесс оказывается испорченным.

Прямые измерения характеристик процесса сопряжены со значительными трудностями из-за высокой рабочей температуры, больших массы и размеров установки. Это обуславливает интерес к численному моделированию течений в реакторе. Зная их структуру на различных стадиях процесса, можно формировать поток металла таким образом, чтобы обеспечивалось более устойчивое протекание реакции. Первые попытки определить интенсивность конвективных течений в реакторе на основе численного моделирования конвекции магния в цилиндрическом сосуде были предприняты почти 40 лет назад [13, 14]. Расчеты выполнялись для сильно заниженных значений числа Грасгофа — 105 вместо 1012 , что заставляет с осторожностью относиться к сделанным оценкам скорости в реальном реакторе. Недавно были получены результаты численного моделирования конвекции магния в цилиндре для реалистичных значений управляющих параметров [15], однако расчеты проводились для стационарного осесимметричного случая.

Цель данной работы — создание гидродинамической модели процесса в трехмерной постановке задачи с адекватным учетом особенностей турбулентного течения и исследование с ее помощью особенностей конвекции в реакторе при различных режимах подогрева и охлаждения.

2.    Постановка задачи и математическая модель

В работе рассматривается конвективное течение в реакторе только одной фазы — жидкого магния. При этом не учитывается вклад второй жидкой фазы — хлористого магния, и пористой среды — титановой губки, которые оседают на дно реактора. Трехмерная математическая модель основывается на уравнениях термогравитационной конвекции для однофазной среды в приближении Буссинеска. Используется LES (Large Eddy Simulation) подход для учета турбулентности, а именно модель Смагоринского [16]. В рамках этого подхода крупные масштабы турбулентного течения рассчитываются явно, а вклад более мелких вихрей учитывается неявным образом путем подсеточного замыкания, согласно которому мелкомасштабная турбулентность параметризуется через характеристики крупномасштабного течения с привлечением эмпирических коэффициентов.

Уравнения для крупномасштабного течения получаются посредством применения процедуры фильтрации уравнений тепловой конвекции. Характерный масштаб А для фильтра обуславливается размером расчетной сетки, то есть А = ( h_xh y h_z )^Z , где h_x, h y , h_z — размер шага сетки по каждой из осей декартовой системы координат. Вихри с размером большим чем А , считаются «крупными», а вихри с размером меньшим А — «мелкими», вклад от которых и нужно моделировать.

Система уравнений, описывающих крупномасштабное течение, имеет вид:

+ v -V v d t

- ¹ V P + v eff A v + g P T e _z , P

V- v = 0,

ST

- + v-VT = xfAT .

Здесь: t — время; v — вектор скорости движения жидкости; P — давление (отклонение от гидростатического давления P0); T — температура (отклонение от среднего значения Т0); р — среднее значение плотности; g — ускорение свободного падения; в — температурный коэффициент объемного расширения; ez — единичный вектор, направленный вдоль оси z . При этом вместо коэффициентов кинематической вязкости v и температуропроводности х в уравнениях присутствуют эффективная вязкость veff и эффективная температуропроводность хeff соответственно. Эффективная вязкость определяется выражением veff = v + vt, где vt = CS A2 |S| — турбулентная вязкость (Cs — постоянная Смагоринского, |S| — норма тензора скорости деформации S = (Vv + (Vv )T)J'S). Эффективная температуропроводность находится по формуле хef = vt/Prt + v/Pr, где Prt — турбулентное число Прандтля. В расчетах принимаются следующие значения: Cs = 0,14 ; Prt = 0,9 .

Реторта для восстановления титана имеет радиус 0,75 м и заполняется жидким магнием до уровня 2,5 м. Верхняя часть боковой поверхности обдувается холодным воздухом, высота зоны охлаждения составляет 0,7 м. Схема расчетной области и система координат показаны на рисунке 1 а . Расчетная область представляет собой цилиндр радиусом R , высотой H , охлаждаемой верхней частью боковой поверхности высотой h .

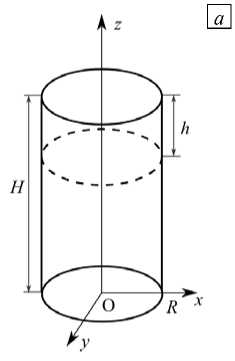
Рис. 1. Схема расчетной области: общий расчетной сетки (в)

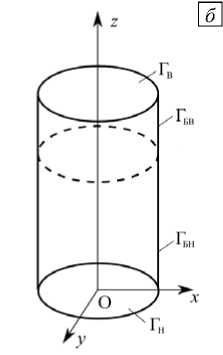
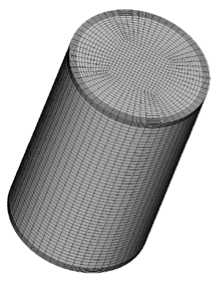
в вид (а), вертикальное сечение xz с обозначениями границ (б); структура

На рисунке 1 б обозначено: Г В — верхняя поверхность площадью S _В; Г _БВ — часть охлаждаемой боковой поверхности, площадью S _БВ ; Г _НВ — нижняя часть боковой поверхности площадью S _НВ, Г _Н — основание площадью S _Н . Все границы области считаются твердыми, для скорости задаются условия прилипания на всех границах ( v = 0).

Вид условия для скорости на свободной верхней границе Г В заслуживает отдельного обсуждения. В жидких металлах на свободной поверхности возникают пленки [17], поэтому в расчетах, как правило, полагают, что здесь имеет место прилипание. Однако в случае химической реакции выполнение этого условия далеко не очевидно. Чтобы прояснить вопрос о влиянии вида граничных условий для скорости на структуру течения, был проведен ряд расчетов с проскальзыванием на верхней границе. Оказалось, что при этом интенсивность течения вблизи свободной поверхности несколько выше по сравнению с течением при прилипании, но структура течения принципиально не меняется. По этой причине в данной работе вычисления проводились с использованием для скорости условия прилипания на верхней границе.

В расчетах рассматриваются три различных вида тепловых граничных условий (ТГУ) — три конфигурации подогрева. Первой конфигурации — ТГУ-1 (Рис. 2 а ), соответствует ситуация, при которой на поверхности металла протекает реакция с тепловой мощностью Q_P , в верхней части массив металла через боковую поверхность охлаждается воздухом, нагреватели в печи выключены. В этом случае

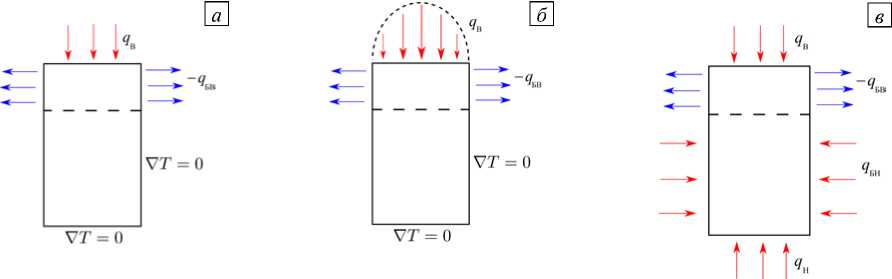
Рис. 2. Схемы распределения тепловых потоков на границах расчетной области для различных конфигураций подогрева: ТГУ-1, равномерный нагрев от реакции ( а ); ТГУ-2, неравномерный нагрев от реакции по параболическому закону ( б ); ТГУ3, нагрев от реакции и от нагревателей в печи ( в )

на верхней границе цилиндра Г В задается постоянный поток тепла q В , с боковой поверхности Г _БВ отводится постоянный поток тепла - q БВ , нижняя часть боковой поверхности Г _БН и основание Г Н считаются теплоизолированными. Итак, ТГУ-1 имеют вид:

дT  _  _Qp     дT        _  Qp д T д n

= 0.

^Г БН , ^Г Н

a       q Вс, л         q бв     с дn гв        0В       дn Г             о бв

Вторая конфигурация — ТГУ-2 (Рис. 2 б ), аналогична первой, за исключением того, что тепловой поток на верхней границе Г В распределен не равномерно, а по параболическому закону с максимумом в центре и минимумом на периферии. ТГУ-2 берутся для того, чтобы исследовать вопрос о влиянии неравномерного распределения потока тепла на поверхности расплавленного металла Г _В на структуру конвективного движения в реторте. Подобная температурная неоднородность может возникать в реакторе во время реального процесса восстановления титана вследствие неравномерности распыления тетрахлорида титана на поверхность магния. Следовательно, ТГУ-2 имеют вид:

д T          2 Q„ Г    ( x ² + у ²) )

= q в =т Р 11 —^2— I , д n _г          o _R I R )

Г В               В X                  /

д T           Qp я         q бв     с , дn ГБВ             0БВ

д T д n

= 0.

^Г БН , ^Г Н

Третья конфигурация — ТГУ-3 (Рис. 2 в ), сочетает в себе нагрев сверху на границе Г _Вс постоянным потоком тепла q _В от химической реакции с тепловой мощностью Q P , нагрев снизу на границе Г Н с потоком тепла q _Н от нижнего нагревателя мощностью Q _Н , и нагрев нижней части боковой поверхности Г _БН с потоком тепла q _БН от боковых нагревателей с общей мощностью Q _БН. Все это тепло отводится от реторты путем охлаждения границы Г _БВ. Таким образом, ТГУ-3 имеют вид:

д T      _ Q p  д T   _         ( Q p + Q БН + Q Н )

р q Be,,         q бв дn Гв        0 в   дn Г

д T        Q™       д TQ

БНН q БН    с ,                   q Нс дn г          0гн         дn г 0н

1 БН                БН                    1 Н

Первая и третья конфигурации соответствуют двум крайним ситуациям: первая — выделению тепла только в результате реакции при отключенных нагревателях в печи; третья — подаче тепла от всех одновременно работающих нагревателей в печи. Для качественных оценок структуры течения рассмотренные конфигурации наиболее показательны, хотя следует отметить, что в реальном процессе восстановления титана возможны и другие режимы нагрева, в частности, одновременно могут включаться только отдельные секции нагревателя печи. Во всех расчетах контролировалось соблюдение интегрального теплового баланса в реакторе.

Управляющими параметрами в данной задаче являются число Грасгофа Gr и число Прандтля Pr . Число Грасгофа, подобно работе [13], находится через поток тепла на верхней границе: Gr = g в q _В R ⁴/(v ² k ) , где характерный перепад температуры есть q _В Rk , k — коэффициент теплопроводности жидкости. Такой способ определения числа Грасгофа оправдан для ТГУ-1 и 2, представленных на рисунках 2 а , б , но он не учитывает вклад от нагревателей печи в конфигурации, отвечающей ТГУ-3 (Рис. 2 в ). Далее при обсуждении результатов будут использоваться и размерные, и безразмерные величины.

Дискретизация уравнений проводится по методу конечных объемов. Для решения полученной системы уравнений применяется алгоритм PISO (Pressure Implicit with Splitting of Operators) [18], основанный на процедуре коррекции давления. Расчетная сетка содержит совмещенные узлы (collocated grid), то есть значения всех переменных вычисляются в одних и тех же узлах [19]. Дискретизация слагаемых с производными по времени осуществляется с помощью неявной схемы Эйлера. Конвективные слагаемые рассчитываются по схеме с уменьшением полной вариации TVD (Total Variation Diminishing) и ограничителем потока, предложенным Швеби [20]. Данная схема обладает свойствами транспортивности и ограниченности, имеет второй порядок точности аппроксимации [21]. Дискретные аналоги диффузионных слагаемых строятся на основе расчетной схемы с центральными разностями. В совокупности неявная консервативная расчетная схема представляет исходную систему дифференциальных уравнений с первым порядком точности по времени и со вторым порядком точности по координате. Для решения системы линейных алгебраических уравнений применяется метод бисопряженных градиентов BiCG (Biconjugate Gradient Method) [22]. Во всех основных расчетах сетка имеет блочную регулярную структуру с общим числом узлов 5 млн и является неравномерной (Рис. 1 в ) с минимальным шагом вблизи границы (3 мм) и большим пространственным шагом во внутренней части реторты (до 10 мм). Измельчение сетки в окрестности границы необходимо для того, чтобы корректно разрешать температурный и скоростной пограничные слои. Число Куранта в расчетах не превышает 0,5. Для реализации описанной численной схемы применяется свободно распространяемый пакет программ с открытым исходным кодом OpenFOAM Extend 3.1.

Расчеты проводились на вычислительном кластере «Тритон» ИМСС УрО РАН (г. Пермь) и на суперкомпьютере «Уран» ИММ УрО РАН (г. Екатеринбург). Ускорение работы параллельного алгоритма относительно времени счета на одном процессоре составило: на 8-ми процессорах — в 5,5 раз; на 32-х процессорах — в 14,2 раза; на 128-ми — в 43,8 раза; на 160-ти процессорах — в 62,6 раз. Для расчета 1 секунды времени физического процесса при Gr = 2,2 - 10 ¹² требовалось 240 секунд машинного времени на 160-ти процессорах. Для адекватной оценки средних полей и статистических характеристик пульсаций необходим интервал осреднения с длительностью не менее 2000 секунд.

3.    Результаты расчетов

При вычислениях основными задаваемыми параметрами были конфигурации подогрева (Рис. 2) и значения подводимых и отводимых потоков тепла, с которыми связано число Грасгофа. Расчеты выполнялись для широкого диапазона чисел Грасгофа от Gr = 2,2 - 10 7 (при малом подогреве) и до Gr = 2,2 - 10 ¹² (при реальном процессе в реакторе). Такие режимы нагрева выбрались для того, чтобы проследить, как качественно меняется структура течения при изменении интенсивности нагрева, и определить границы применимости для данной задачи осесимметричных стационарных математических моделей. Конвективные параметры среды соответствовали жидкому магнию при температуре 850 ° С и составляли: число Прандтля Pr = 0,008; кинематическая вязкость v = 4,87 - 10 7 м²/с; коэффициент температурного расширения в = 1,7 - 10 ^{- 4} K^-1 [23].

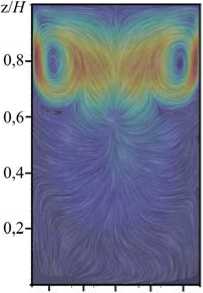
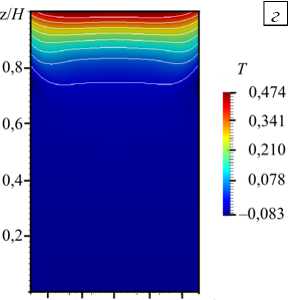
На рисунке 3 приведены результаты расчетов при наименьшем из рассмотренных значений числа Грасгофа — Gr = 2,2 - 10 ⁷ , для заданных конфигураций нагрева. При равномерном нагреве сверху (ТГУ-1) в реторте устанавливается стационарное осесимметричное течение с кольцевым вихрем в верхней части (Рис. 3 а , здесь и далее в качестве характерной единицы для скорости выбрана величина v/ R ). Следует отметить, что вихрь примыкает к верхней границе области не вплотную, а несколько отстоит от нее. Из рисунка 3 г , на котором изображено поле температуры для данного случая, можно видеть, что значительный горизонтальный градиент температуры возникает в пограничном слое, в то время как в центральной части цилиндра изотермы близки к горизонталям. Такая структура поля температуры качественно совпадает с результатами работы [13] для подогрева сверху.

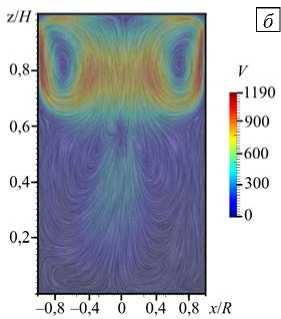
При неравномерном нагреве (ТГУ-2) вихрь в верхней трети массива металла примыкает к верхней границе и становится более интенсивным (Рис. 3 б ). Это различие объясняется тем, что неравномерный нагрев создает дополнительный горизонтальный температурный градиент вблизи верхней границы (Рис. 3 д ).

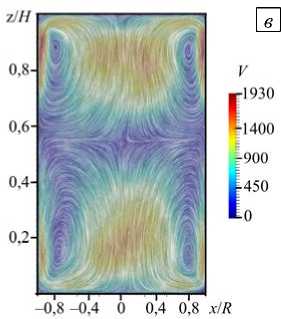
Ситуация существенно меняется, если в дополнение к нагреву сверху добавляется нагрев в нижней части и на боковой поверхности реторты (ТГУ-3). Движение перестает быть стационарным, поэтому на рисунках 3 в , е представлены осредненные по времени поля скорости и температуры. Течение приобретает двухвихревую структуру (Рис. 3 в ), верхний и нижний вихри имеют близкие размеры, максимальные скорости двукратно возрастают по сравнению со скоростями в случае без дополнительных нагревателей.

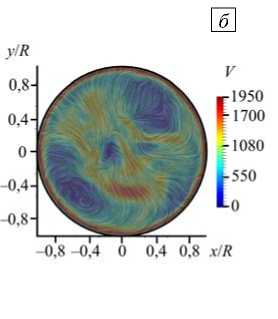
Проследим за изменением структуры течения при постепенном увеличении числа Грасгофа, рассматривая только нагрев сверху (ТГУ-1). С ростом числа Грасгофа течение становится нестационарным и теряет осевую симметрию. На рисунках 4 а , б показаны примеры мгновенных полей скорости

-0,8 -0.4 0 0,4 0,8 x/R

-0.8 -0.4 0 0.4 0.8 x/R

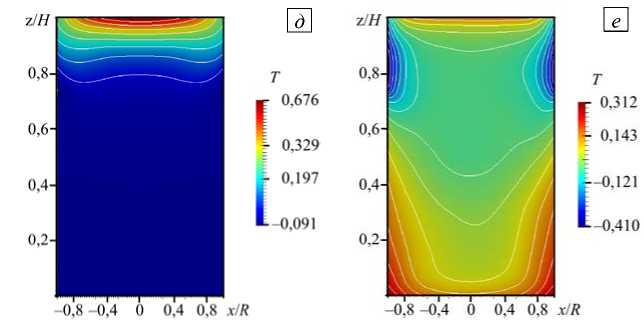
Рис. 3. Поля скорости ( а - в ) и температуры ( г - е ) в сечении xz при Gr = 2,2 - 10 7 , отвечающие различным конфигурациям нагрева: ТГУ-1 ( а , г ); ТГУ-2 ( б , д ); ТГУ-3 ( в , е )

для Gr = 2,2 - 10 8 . Интенсивность вихря в верхней части цилиндра выросла, сам вихрь несколько сдвинулся вниз, а температурный погранслой стал тоньше (Рис. 4 в ). Следует отметить, что нахождение точной границы потери стационарности и осевой симметрии не входило в основные цели работы, поскольку эта граница находится в области со значениями управляющих параметров заведомо более низкими, чем в реальном аппарате восстановления титана.

Увеличение числа Грасгофа сопровождается дальнейшим ростом скорости течения и размера вихря. На рисунке 5 приведены результаты расчетов для Gr = 1,1 - 10 ¹⁰ . Движение приобрело выраженный погранслойный характер. Конвективное течение в объеме верхней трети цилиндра, за исключением тонкого пограничного слоя, практически исчезло (Рис. 5 а , б ). Это объясняется тем, что здесь установился близкий к равномерному вертикальный градиент температуры без неоднородности в горизонтальном направлении (Рис. 5 в ). Существенный горизонтальный градиент температуры возник только вблизи границы раздела между охлаждаемой и теплоизолированной частями боковой поверхности (Рис. 5 г ). При этом течение в нижней части реторты осталось достаточно интенсивным и нестационарным.

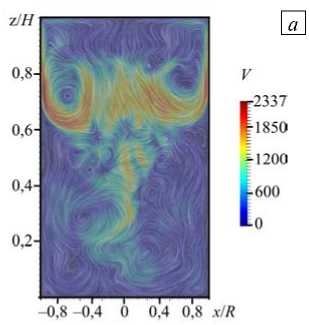
Рис. 4. Результаты для конфигурации

0.8 -0.4 О 0.4 0.8 x/R

нагрева ТГУ-1 при Gr = 2,2 - 10 8 : мгновенные поля скорости в сечении xz ( а )

и в сечении xy на высоте z = 0,8 H ( б ); поле температуры в сечении xz ( в )

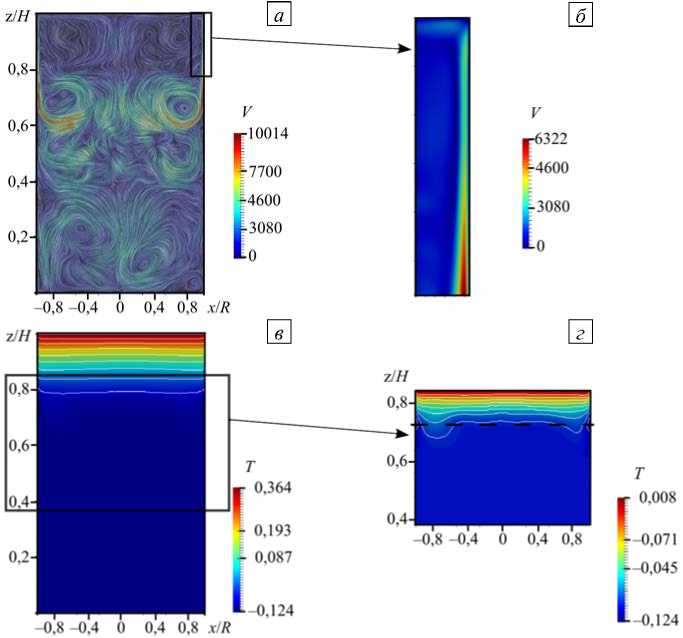
Рис. 5. Результаты для конфигурации нагрева ТГУ-1 при Gr = 1,1-1010 в сечении xz : мгновенное поле скорости (а) и его увеличенный фрагмент (б); поле температуры (в), и его увеличенный фрагмент (г)

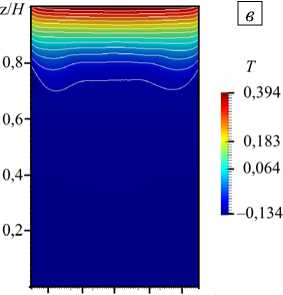
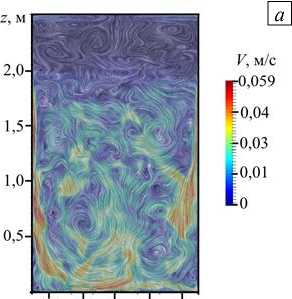
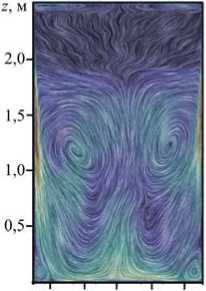
Реальному процессу восстановления титана в реакторе соответствует число Грасгофа Gr ® 2,2 ■ 10 ¹² . На рисунках 6 а , б приведены поля скорости для такого режима течения при неоднородном нагреве сверху (ТГУ-2). Структура течения качественно не меняется по сравнению со случаем Gr = 1, Г10 ¹⁰ , течение в верхней трети расчетной области по-прежнему подавляется, но интенсивность движения в нижней части возрастает, турбулентное течение занимает весь объем ниже зоны охлаждения. В размерных единицах для реторты радиусом R = 0,75 м при заполнении ее металлом на высоту H = 2,5 м и высотой охлаждаемой части боковой поверхности h = 0,7 м скорости течения в погранслое достигают 6 см/с, а значение скорости

0,6 -0,3 О 0,3 0,6 х, м

-0,6 -0.3 О 0,3 0,6 х, м

Рис. 6. Результаты для конфигурации нагрева ТГУ-2 при Gr = 2,2 ■Ю¹²: мгновенное ( а ) и осредненное по времени ( б ) поля скорости в сечении xz ; поле температуры вблизи верхней границы расчетной области в сечении xy ( в ); поле температуры в сечении xz в верхней части массива магния ( г )

в

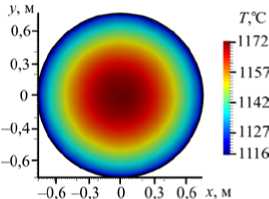
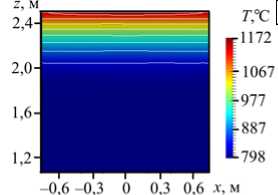
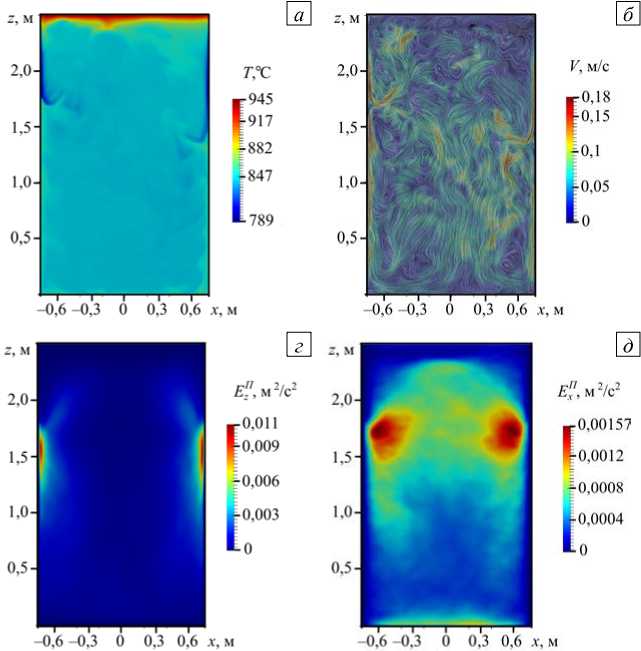
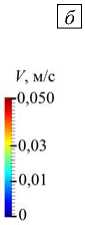
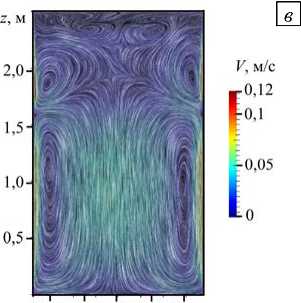
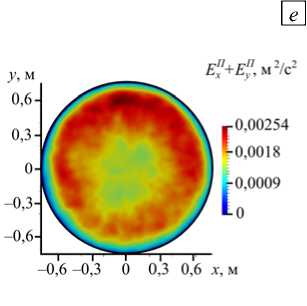
Рис. 7. Результаты для конфигурации нагрева ТГУ-3 при Gr = 2,2 ■ 10¹²: мгновенное поле температуры ( а ), мгновенное поле скорости ( б ), осредненное по времени поле скорости ( в ), вертикальная компонента энергии пульсаций скорости E_z ^П ( г ), и горизонтальная компонента пульсаций скорости Е П ( д ) в сечении xz ; поле пульсаций скорости ( Е ^ + E " ) в горизонтальной плоскости xy при z = 0,72 H ( е )

-0,6-0,3 О 0,3 0,6 х, м

в центральной части реторты составляет ® 4 см/c. На рисунке 6 б , представляющем среднее по времени поле скорости для данного режима, хорошо различим круговой вихрь в нижней части реторты. Скорости достигают максимальных значений в погранслое у боковой стенки на высоте 0,7–1,7 м.

Важно, что неравномерность распределения потока тепла на верхней границе расчетной области в данном режиме не оказывает принципиального влияния на структуру течения: изотермы в ее верхней части уже на удалении 5 см от поверхности становятся практически горизонтальными (Рис. 6 в , г ).

Стоит отметить, что в области наибольших градиентов температуры (в верхней трети массива металла) естественно ожидать возникновения наиболее интенсивных вихрей. Однако при реальных параметрах процесса этого не наблюдается. Показано, что градиент температуры, вызванный реакцией на поверхности, действительно поддерживает кольцевой вихрь в верхней части цилиндра при малых числах Грасгофа, но подавляет его при числах Грасгофа, отвечающих реальному процессу восстановления титана.

Включение дополнительного нагрева нижней части реторты существенно меняет характер течения. На рисунке 7 приведены результаты расчета с конфигурацией нагрева ТГУ-3 при реальных параметрах процесса в реакторе, когда нагреватели в печи работают на полную мощность, равную 423 кВт, из которых подогрев снизу составляет QН = 94 кВт, подогрев на боковой поверхности в нижней ее части — QБН = 329 кВт; тепловая мощность реакции на поверхности равняется Qp = 205 кВт. При таком тепловом режиме равномерный вертикальный градиент температуры в верхней части цилиндра не устанавливается. Поле температуры (Рис. 7а) отражает нестационарный характер движения, обусловленного подъемным пристеночным течением от нагреваемой нижней части реактора и опускным течением, возникающим в охлаждаемой части реторты. Граница между этими потоками не стационарна и смещается вверх-вниз. На картинах мгновенных полей скорости (Рис. 7б) можно видеть, что турбулентное течение занимает весь объем расплавленного металла. На среднем по времени поле скорости (Рис. 7в) хорошо различима двухвихревая структура конвективного течения — один кольцевой вихрь в верхней части расчетной области и один в нижней части. Граница раздела между вихрями находится на высоте 0,72 H, то есть на границе между охлаждаемой и нагреваемой частями боковой поверхности цилиндра. Можно видеть, что центр вихрей сдвинут к боковой границе, максимальной интенсивности (12 см/c) вихри достигают вблизи границ. В центральной части верхней трети цилиндра интенсивность течения мала, а в остальном объеме наблюдается подъемное течение со средней скоростью ® 7 см/c. При этом максимальная мгновенная скорость Vmax вблизи границы достигает 20 см/c.

Интерес представляет и распределение пульсаций скорости на фоне среднего течения. На рисунке 7 г демонстрируется поле пульсаций E_z ^П вертикальной компоненты скорости V_z в вертикальном сечении yz расчетной области. Из рисунка следует, что наибольшие пульсации имеют место в узкой кольцевой области толщиной ® 5 см вблизи границы между охлаждаемой и нагреваемой частями боковой поверхности. На рисунке 7 д представлено поле пульсаций E_x ^П горизонтальной компоненты скорости V_x в вертикальном сечении yz . Горизонтальные пульсации скорости также имеют максимумы вблизи границы раздела, но области со значительной величиной пульсаций распределены по большему объему. Следует отметить, что пульсации вертикальной компоненты скорости интенсивнее горизонтальных пульсаций скорости (максимальные значения отличаются в семь раз). На рисунке 7 е приведено поле пульсаций скорости ( Е П + Е П ) в плоскости xy на высоте z = 0,72 H . В горизонтальном сечении пульсации распределены по радиусу относительно однородно их максимальные значения находятся внутри кольца 25 см <  r <  65 см.

На рисунке 8 представлены примеры зависимости температуры от времени в отдельных точках расчетной области. Наиболее интенсивные пульсации температуры возникают вблизи боковой стенки около границы раздела охлаждаемой и нагреваемой частей боковой поверхности. В точке, расположенной на расстоянии 1 см от боковой поверхности и на высоте 2,3 м максимальные значения амплитуды пульсаций температуры достигают 50 ° С (Рис. 8 а ). При этом интенсивность пульсаций зависит от времени: периоды с большой и малой амплитудой чередуются (Рис.8 а , линия 2 ). Обнаружено, что в центральной части цилиндра значения амплитуды существенно меньше, чем около боковой поверхности. В точках на оси реторты наибольшая величина амплитуды пульсаций температуры наблюдается вблизи верхней границы (Рис. 8 б , линия 1 ), и чем дальше от верхней границы находится точка, тем меньше в ней амплитуда пульсаций.

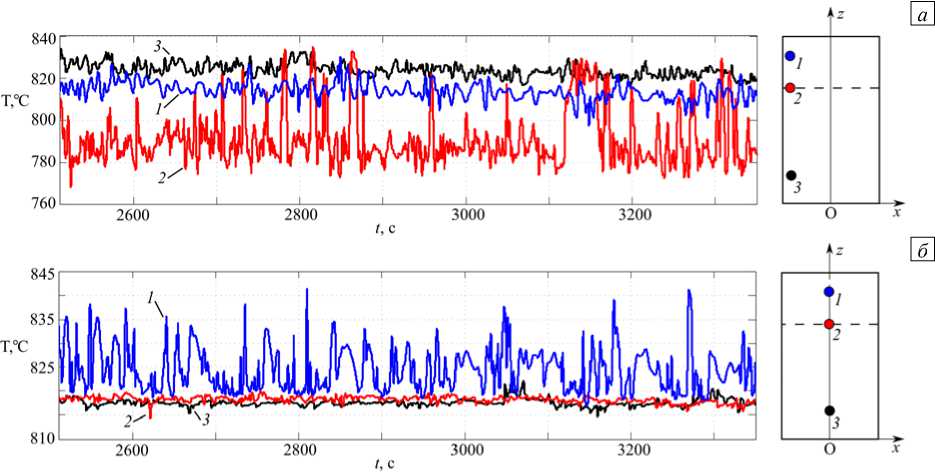
Рис. 8. Результаты для конфигурации нагрева ТГУ-3 при Gr = 2,2 ■ 10¹²: зависимости температуры от времени в отдельных точках расчетной области, находящихся на расстоянии 1 см от боковой стенки ( а ) и на оси ( б ) (см. схемы справа); линии 1 соответствуют точкам на высоте z = 2,3 м, линии 2 - точкам на высоте z = 1,8 м, линии 3 - точкам на высоте z = 0,3 м

На рисунке 9 а представлены спектральные плотности энергии пульсаций вертикальной компоненты скорости V_z в различных точках расчетной области. Видно, что ее пульсации вблизи боковой поверхности обладают большей интенсивностью по сравнению с пульсациями в центре во всем диапазоне частот. На рисунке 9 б приведены спектральные плотности энергии пульсаций температуры. На высоте 1,8 м пульсации температуры вблизи боковой границы и в центре отличаются на два порядка (линии 1 и 2 ), а на высоте 2,3 м спектры пульсаций вблизи границы и в центре практически совпадают (линии 3 и 4 ). На обеих частях рисунка 9 прямой линией показан наклон « - 5/3», соответствующий колмогоровскому закону. Наклон показан для справки, так как интерпретации в терминах однородной и изотропной турбулентности, особенно вблизи границ расчетной области, требуют большой осторожности, несмотря на то, что такой наклон наблюдается в интервале частот, превышающем декаду.

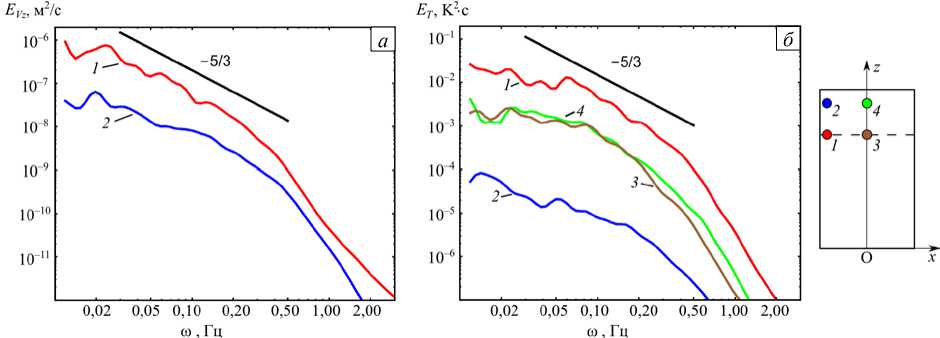
Рис. 9. Результаты для конфигурации нагрева ТГУ-3 при Gr = 2,2 - 10¹²: спектральные плотности энергии пульсаций вертикальной компоненты скорости V_z ( а ) и температуры ( б ) в отдельных точках расчетной области (см. схему справа): линиям 1 и 2 отвечают точки, находящейся в 1 см от боковой стенки на высотах z = 1,8 м и z = 2,3 м, линиям 3 и 4 -точки, находящейся на оси на высотах z = 1,8 м и z = 2,3 м

Приведенные характеристики турбулентных пульсаций показывают, что среднее течение формируется на фоне развитой турбулентности, и мгновенные поля скорости и температуры значительно отличаются от средних. В этих условиях использование полной трехмерной модели становится принципиальным. Хотя средние поля и получаются осесимметричными, трехмерность задачи необходима для адекватного учета турбулентности, так как LES модели разработаны именно для трехмерного случая. Вычисления в стационарной осесимметричной постановке [15] также показывали, что при включенных нагревателях наиболее интенсивное конвективное движение вызывается перепадом температуры вблизи границы раздела охлаждаемой и нагреваемой частей боковой поверхности цилиндра, а общая структура осредненного течения имеет двухвихревой вид. Однако форма и размеры вихрей при расчетах в полной постановке отличаются существенно, демонстрируя, что при больших значениях Gr течение носит ярко выраженный погранслойный характер, и центры вихрей сдвигаются к боковой границе реторты.

4.    Заключение

Выполнено численное исследование структуры конвективного течения расплавленного магния в реакторе восстановления титана для широкого диапазона чисел Грасгофа (от Gr = 2,2 - 10 7 до 2,2 - 10¹²). Задача решена в трехмерной нестационарной постановке, что позволило вычислить мгновенные и средние характеристики процесса, проанализировать поля пульсаций скорости и температуры.

Обнаружено, что режимы со стационарным и осесимметричным течением в реакторе возможны только при существенно заниженных значениях управляющих параметров. При параметрах, отвечающих реальному процессу, в реторте возникают нестационарные турбулентные режимы течения.

Градиент температуры, вызванный химической реакцией на поверхности, поддерживает кольцевой вихрь в верхней части массива металла при малых числах Грасгофа, но подавляет его при числах Грасгофа, соответствующих процессу восстановления в реакторе.

Проведены расчеты для двух конфигураций нагрева в реакторе: с нагревателями печи, работающими на полную мощность и отключенными. Показано, что в этих двух случаях структуры конвективного течения принципиально различаются. Следовательно, с помощью изменения режимов нагрева реторты можно влиять на течение с целью создания наиболее благоприятных условий для протекания реакции.