Численное исследование минимумов термодинамического потенциала сегнетоэлектрика титаната бария

В последние годы развитие теории и приложений сегнетоэлектрических материалов идёт быстрыми темпами. В теории сегнетоэлектричества обозначалось существенное расширение возможностей применения классической теории Ландау для описания свойств низко-и наноразмерных объектов, кристаллов с неоднородным распределением поляризации, связанным с доменной структурой и поверхностной релаксацией, неоднородным распределением примесей и дефектов. Увеличился поток работ, связанных с расчётами из первых принципов, позволяющих вплотную подойти к выяснению природы сегнетоэлектрических явлений. С другой стороны, в связи с появлением и развитием новых методов сильно расширялись возможности экспериментального исследования физических свойств, доменной и кристаллической структуры объёмных и нано-структурированных сегнетоэлектриков, муль-тиферроиков. Несомненно, прорывным направлением стало получение, исследование и применение сегнетоэлектриков в виде тонких плёнок, сверхрешёток и композитов [1] .

При этом постоянно возрастает роль новых теоретических подходов в исследовании свойств и структуры сегнетоэлектрических материалов.

Материалы и методы исследования

В работе [2] был предложен топологический метод исследования закономерностей при фазовых переходах в сегнетоэлектрических кристаллах и нелинейных явлениях, основанный на представлениях о клеточных комплексах системы особых точек термодинамического потенциала. Построена полная совокупность клеточных комплексов для титаната бария. Для BaTiO 3 было использовано разложение потенциала Ландау–Девоншира до шестого порядка, предложенное в работе [3] . Исследованы фазовые переходы, индуцированные внешним электрическим полем. Однако, быстрое развитие экспериментальной базы и активные теоретические исследования в этом направлении привели к существенному уточнению параметров потенциала. В работе [4] предложены исправленные разложения потенциала Ландау–Девон-шира до шестого порядка и альтернативные разложения до восьмого порядка:

\  7   2 j i j 4 \/ ijkl     mrnnor ^mmjij-o-orki ) i j k l 6  ijklmn ijklmnV /

G  Ui(P + P2 + P3 ) + F + Um(Pi + P2 + P3 ) + UU2(Pi (P2 + P3 ) + P2 (P + P3 ) + P3 (P + P2 )) + U^P P2 P

F4 = 1 («12 - 4C12Q12Q11 - 4cuQ12Q11 - 2C12Qf1 - 6C12Q - 2C11Q12216c44Q424 ) (P^P^^ + P3 P^ + P3 P^+

2(3)

1         2   22444

⁺ 4 ^{( a} 11   ^oc 12 Q 12 ^Q 11    chQ ^Q11   ^^c 12 Q 12   ^^c 11 Q 12/V1 ^{+ v}2 ^{+ 1} 3 )

где P ( P 1 , P 2 , P 3 ) – вектор спонтанной поляризации, c_ijkl , Q_ijkl – компоненты тензора упругих модулей и электрострикционных коэффициентов соответственно, применены стандартные упрощения записи суммирования по Ландау.

При отсутствии напряжений формула (3) существенно упростится:

F 4 = 2 ^a 12 ( P 1 ^P 2 ⁺ P 1 ^P 3 ^{+ P} 2 ^P 3 ) ⁺ 4 ^a 11 ( P 1 ^{+ P} 2 ^{+ P} 3 ) ⁽⁴⁾

Для случая потенциала восьмого порядка к свободной энергии (2) прибавится слагаемое:

8 8 8    622 622 622    444444

^F 8 = « 1111 ^{( P} 1 ⁺ P 2 ⁺ P 3 ) ⁺ « 1112 ( ^P 1 ⁽ P2 ⁺ P 3 ) ⁺ P 2 ^{( P} 1 ^{+ P} 3 ) ^{+ P} 3 ^{( P} 2 ^{+ P} 1 ) ) ⁺ « 1122 ^{( P} 1 ^P 2 ^{+ P} 1 ^P 3 ^{+ P} 3 ^P 2 )

222  2   2   2

^{T U} 1123 P 1 P 2 P 3 ( P 1 ⁺ P 2 ⁺ P 3 )

В таблице 1 приведены два набора коэффициентов для (1) и (2). Упругие и элек-трострикционные коэффициенты приведены отдельно в таблице 2. В таблицах, взятых из [1, 2, 4] выбраны усреднённые значения.

Известно [5], что при понижении температуры в кристаллах титаната бария происходит ряд последовательных сегнетоэлектрических фазовых переходов: при 393 °K они переходят из кубической (параэлектрической) фазы с пространственной группой Pm3m в тетрагональную полярную (сегнетоэлектрическую) с пространственной группой P4mm, затем при 278 °K следует переход в орторомбическую полярную с пространственной группой Amm2 и, наконец, при 183 °K – в ромбоэдрическую полярную с пространственной группой R3m. Все три перехода – первого рода, и при изменении температуры диэлектрическая проницаемость меняется скачками.

Таблица 1

Коэффициенты разложения термодинамического потенциала Ландау–Девоншира для BaTiO 3 (в единицах СИ, Т в К)

Table 1

The expansion coefficients of thermodynamics potential the Landau–Devonshire for BaTiO 3 (in SI, T, K)

Коэффициенты Coefficients	Шестой порядок Sixth order	Восьмой порядок Eighth order
« 1 (10 5 Кл-2м2Н)	3.34 (Т – 381)	4.124 (Т – 388)
« 11 (10 6 Кл-4м6Н)	4.69 (Т – 393) – 202	– 209.7
« 12(10 8 Кл-4м6Н)	3.23	7.974
« 111 (10 7 Кл-6м10Н)	– 5.52 (Т – 120) + 276	129.4
« 112 (109 Кл-6м10Н)	4.47	– 1.950
« 123 (10 9 Кл-6м10Н)	4.919	– 2.5009
« 1111 (1010Кл-8м14Н)	0.0	3.863
« 1112 (1010 Кл-8м14Н)	0.0	2.529
« 1122 (1010 Кл-8м14Н)	0.0	1.637
« 1123 (1010 Кл-8м14Н)	0.0	1.367

Таблица 2

Упругие электрострикционные коэффициенты для BaTiO 3

Table 2

Electrostriction elastic coefficients for BaTiO 3

Коэффициенты Coefficients	Значение Value
c 11 (1011Нм-2)	1.78
c 12(1011Нм-2)	0.964
c 44 (1011Нм-2)	1.22
Q 11 (Кл-2м4)	0.10
Q 12 (Кл-2м4)	–0.04
Q 22 (Кл-2м4)	0.045

Для потенциала 6 порядка ранее [2] температуры этих переходов получались с удовлетворительной точностью (в пределах 2 градусов).

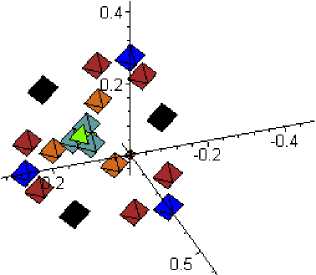
На первом этапе нашего исследования рассмотрен потенциал восьмого порядка для свободного образца. На следующем рисунке приведён пример пространственного расположения экстремумов потенциала в пространстве вектора поляризации. Для указанной на рисунке температуры перечислены все положения равновесия в первом октанте. Справа указаны значения потенциала (G∙10 ⁸ Дж) в порядке возрастания.

При данной температуре кристалл находится в орторомбической фазе с пространственной группой Amm2. Соответственно, минимумы потенциала расположены в координатных плоскостях, направление на них составляет угол 45 ° с осями координат.

Т= 260

^-.3600е-1 ^-.33726-1 ^-.3351 е-1 ^ 3299е-1 ^ 3

^ 32896-1

♦ 0.

Рисунок 1. Положение экстремумов термодинамического потенциала. Справа указаны значения потенциала, умноженные на 10-8

Figure 1. Positions of extrema of thermodynamic potential. On the right side the potential data multiplied on 10-8

Введём следующие обозначения для направлений на точки минимумов: 000 = O, 100= A, 110 = B, 111=C, xxy=D, xy0=E, xyz =F. Последние типы положения экстремумов

(a)

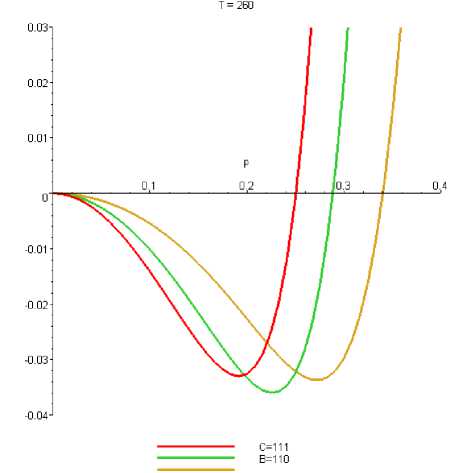
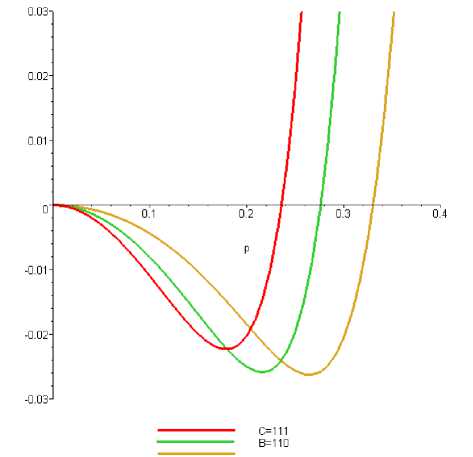
Рисунок 2. Рельефы термодинамического потенциала вдоль симметричных направлений при различных температурах

Figure 2. Thermodynamic potential reliefs along the symmetry directions at different temperatures presented

отвечают пониженной симметрии, в том смысле, что, например, точка D две ненулевых координаты, равных друг другу и третью, отличную от них.

Т = 285

(b)

Показанная на рисунке 1 структура минимумов отвечает «слову» "BAEDCFO", где последовательность букв отвечает возрастанию энергии экстремума. Отметим, что экстремум может быть любого типа. На рисунке 2 показаны кривые потенциала для направлений А, В, С. Хорошо видно, что при повышении температуры от 260 до 285°К минимум рельефа переходит от направления В (орторомбическая фаза) к направлению А (тетрагональная фаза). Результаты вычислений приведены в таблице 3.

Таблица 3

Сравнение структуры потенциального рельефа для различных аппроксимаций термодинамического потенциала

Table 3

Potential relief comparison for the different approximations of thermodynamic potential

Температура, К Temperature, К	8 порядок разложения 8 order polynomial	6 порядок разложения 6 order polynomial
250	BCFAEDO	BCFAEDDBDBO
260	BAEDCFO	BDCAEDDDBBO
270	BAECO	BAECBBO
280	BAECO	BAECBBO
280	BAECO	BAECBBO
281	BAECO	BAECBBO
282	ABECO	BAECBBO
283	ABECO	ABECBBO
290	ABECO	ABECBBO
300	ABECO	ABEBBCO
310	ABCO	ABCO
320	ABCO	ABCO
330	ABCO	ABCO
340	ABCO	ABCO
350	ABCO	ABCO

Из таблицы 3 видно, что фазовый переход происходит между 281 и 282 ° К для потенциала 8 порядка, и это немного лучше согласуется с экспериментальными данными. Следует учесть, что расчёты в таблице 3 не учитывали деформации, возникающие при переполяриза-ции сегнетоэлектрика. Заметим, что точность определения перехода из-за явления сегнетоэлектрического гистерезиса составляет несколько градусов. Из таблицы следует, что потенциал восьмого порядка резко снижает число возможных метастабильных состояний в области использования сегнетоэлектрических кристаллов титаната бария. Для нижних состояний потенциалы демонстрируют вполне ожидаемое