Численное исследование поведения лежащей капли на нагретой плоскости

Исследования динамического поведения лежащей капли в настоящее время вызывают большой интерес. Это связано с важной ролью, которую этот объект играет в технологических процессах, например, при распылении чернил в струйных принтерах, капельном охлаждении поверхностей, росте биологических кристаллов, в тепло-массообменных аппаратах. Математическое описание капли осуществить сложно уже потому, что межфазная поверхность жидкость–газ может свободно двигаться, что подразумевает перестройку вычислительной области на каждом временном шаге. Задача еще более усложняется, если учесть возможность испарения с поверхности жидкости и температурную неоднородность, связанную с поглощением теплоты парообразования на границе жидкость–газ.

В работах по визуализации испаряющейся лежащей капли докладывают о существовании внутренних течений в капле [1], наличии гидротермических волн [2]. В [3] обнаружено уплощение капли в сравнении с равновесной формой при уменьшении объема жидкости из-за испарения. Эксперименты подтверждают факт, что лежащая капля находится в неравновесном состоянии даже в атмосфере своего насыщенного пара, так как из-за кривизны поверхности давление насыщенного пара на ней немного превышает таковое в объеме.

Поверхность испаряющейся капли может перемещаться не только за счет фазового перехода, но также из-за присутствия внутренних течений. Обычно в вычислительных работах неравновес-ностью формы испаряющейся капли пренебрегают. Профиль капли считается равновесным и сферическим (линзоподобным), либо рассчитывается на каждом временном шаге с помощью уравнения Лапласа. Как показывает сравнение результатов численных расчетов с экспериментальными данными, на скорость испарения эти допущения влияют мало, причем как для режима испарения с постоянным радиусом пятна смачивания, так и с постоянным контактным углом [4– 6]. Но существует еще метрологический аспект задачи об испарении лежащей капли. Он связан с тем, что движение неравновесной из-за испарения границы раздела может повлиять на точность измерения поверхностного натяжения методом лежащей капли.

Глобальная цель проводимых авторами исследований – анализ отклонения формы испаряющейся капли от равновесной. Авторы проводят работы поэтапно. В [7] было проведено исследование свободных колебаний лежащей капли, выведенной из положения механического равновесия, и рассчитаны параметры колебаний для капель различных жидкостей. Цель настоящей работы состоит в выяснении влияния температурной неоднородности (нагретая подложка) на движение границы раздела жидкость–газ.

Схема численного эксперимента приведена на рис. 1. Капля жидкости объемом V = 3 n R ³,

R – радиус равновеликой сферической капли, находится на твердой подложке и окружена некон-денсирующимся газом. Границы вычислительной области являются удаленными, т.е. Rk,Hk » R . Приняты следующие приближения: температура подложки постоянна; отсутствует испарение; предполагается осевая симметрия формы капли, распределения давления и течений в капле и газе; граница считается бесконечно тонкой и безинерционной; жидкость является несжимаемой средой; газопаровая смесь описывается приближением идеального газа; коэффициенты переноса являются постоянными в обеих средах; краевой угол является постоянным.

В работе приняты следующие обозначения: ρ l – плотность жидкости, ρ g – плотность газа на удаленных границах, ν_l , ν _g – коэффициенты кинематической вязкости, n l , n g — коэффициенты динамической вязкости, к , K g - коэффициенты теплопроводности, c , c g - удельные теплоемкости, M } , M g - молярные массы, в - коэффициент объемного расширения жидкости, О д , o gs , a s - коэффициенты поверхностного натяжения на границах жидкость–газ, газ–подложка и жидкость–подложка соответственно. Значения коэффициентов переноса считаются постоянными. Здесь и далее индексами l , g и s отмечаются величины, относящиеся к жидкости, газу и материалу подложки.

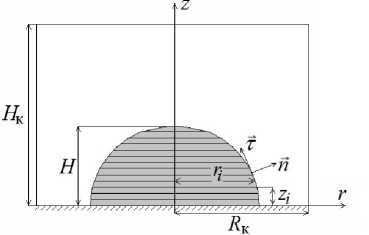
Рис. 1. Схема эксперимента. Капля находится на плоской поверхности в окружении газа

Математическая модель представляет собой систему дифференциальных уравнений сохранения и сопутствующих граничных условий. Система уравнений, описывающих течения в жидкости, содержит уравнения Навье–Стокса, неразрывности и конвективной теплопроводности

IV+(V-V) V3 = - - V P+ v V 2V3 - g3i (T - Ts),(1)

d t

V - V = 0,

—+ v (Vt ) = ^ v2 t .

d t

В (1)-(3) использованы следующие обозначения: V = { v , u } - вектор скорости, P - давление сверх гидростатического, T – температура, g – ускорение свободного падения. В (1) гравитационные температурные эффекты описаны в приближении Буссинеска.

Система уравнений для газовой среды запишется как

— +( V -V ) V = -- V p + ^ g V 2 V ³ - g,                       (4)

d t              p p

I P + V ( p V ) = 0,                                   (5)

d t

—+v ( Vt )=^^ 'V ² t , d t     ^{v 7} pg c g

P =

p RT

M

Здесь буквами p и ρ обозначены давление и плотность газовой среды.

В модели приняты следующие граничные условия:

на оси

r = 0:

d u  d T  d P  d p   d p _A

— = — = — = —=  = 0, v = 0

d r   d r   d r   d r   d r

на твердой границе z = 0:

v = u = 0,

' T s , r <  3 R ,

_ T s - ( T s - T g )/( R k

- 3 R ) - ( r - 3 R ), 3 R <  r <  R _k ,

Физика

на удаленных границах в газовой среде z = Hk or r = R k: v = u = 0, T = Tg, p = Pg, p = Pg .                 (10)

Здесь T g , p g , p g - есть невозмущенные значения температуры, давления и плотности газа на удаленных границах, T s – температура подложки, а условие (9) для температуры выбрано для того, чтобы избежать скачка температуры при z = 0, r = R k .

На границе жидкость–газ выполнены следующие условия [8]:

• 1)    скорости непрерывны

V / = V g , U / = U g ;                                           (^П)

• 2)    нормальные напряжения испытывают скачок, определяемый формулой Лапласа

n T n|/ - P l ( V ■ n - V s g ) ² - ^ n T n g - p ( v g ■ n - V s g ) ² j = a g K ,              (12)

где T ij – тензор напряжений, V S_lg – скорость перемещения границы раздела фаз;

• 3)    скачок касательных напряжений равен касательной составляющей градиента поверхност-

• ного натяжения

?^ T ?b ^- p / V ^ i -T ( V r ?i ^- V s g ) - (?? T ^T| _g - pV_g -T ( y_g ■ n ^- V s g ) ) = - O T ( V T ) _t .

В (13) температурная зависимость поверхностного натяжения описывается формулой a = a - nT (T - To), aT =

d a dT

;

• 4)    температура непрерывна

  T g = T ;

  5) поток тепла в отсутствие испарения непрерывен

  
  
  
  

  _-

  
  

  ■ ki d n + ^p / c /^T/- ( V ^i • n

  
  

  _-

  
  
  
  

  _v \     , d T

  V _S ) - - k g g'      ^g d n

  
  

  k

  
  

  j

  ^{+ p} c g^Tg "( ^vg - n ^{- V}S /g )

  g                       7

  
  

  = 0.

  
  
  
  

Уравнения (12), (13), (15) записаны в системе отсчета, связанной с границей раздела фаз.

Численный метод решения

Для решения системы (1)–(15) использовалась разностная схема, построенная на основе неравномерной пространственной сетки. Уравнения (1), (3) для жидкой фазы записывались в форме законов сохранения, дискретизировались и линеаризовывались. Система полученных алгебраических разностных уравнений решалась методом исключения Гаусса. Система уравнений (4)–(6), описывающая газовую среду, решалась методом прогонки.

В численном решении задачи можно выделить несколько этапов:

• •    минимизацией выражения для механической энергии [9] определяется форма равновесной капли, т.е. набор радиусов { r i } и высота H (рис. 1). Определяются равновесные значения кривизны поверхности капли K 0 ( z i ) . В отсутствие испарения капля имеет постоянный объем, поэтому вычисление { K 0 ( z i ) } проводится только один раз;

• •    определяются давление и скорости в капле путем решения системы уравнений (1, 2, 12, 13). Форма капли, а также скорости и плотность в газе считаются неизменными на этой стадии и берутся из предыдущего временного шага. Система разностных уравнений решается методом исключения Гаусса;

• •    определяется новая форма капли по формулам:

r* ⁺ ^t = r t + v| ■ д t , i = 2, m,         z i ⁺^ t = z t + u I ■ Д t , i = 2, m + 1.

S lg                                                        S lg

Радиус пятна смачивания определяется из условия, что краевой угол не зависит от того, происходит натекание или отток жидкости на подложке, и равен равновесному углу, определяемому уравнением Юнга;

• •    распределение скоростей в газе определяется последовательным решением уравнений (4) с граничными условиями (11);

• •    распределение плотности в газе определяется с помощью решения уравнения (5). Вблизи поверхности жидкости значения плотности газовой среды интерполируются;

• •    распределение температуры в жидкости определяется посредством решения уравнения (3) с граничным условием (15);

• •    вычисляется распределение температуры в газе с помощью решения уравнения (6) с граничными условиями (14);

• •    сетка перестраивается в соответствии с изменениями в форме капли.

Таким образом, использованный численный метод является одним из методов расщепления по физическим процессам [10]. Программный продукт, реализующий указанную схему, был написан на языке Fortran90 и распараллелен с использованием библиотеки MPI. Расчеты проводились на суперкомпьютере «СКИФ-Аврора ЮУрГУ».

Вычисления проводились для следующего набора параметров: R = 0,5 мм, жидкость – вода с als -ags = 0 Н• м-1,        alg = 7,3•Ю-2 Н• м-1,        pl = 1000 кг/м-3,        vl = 1,0-10"6 м2/с, kl = 0,55 Вт/(м• K), el = 1,27 •Ю-3 К-1, Cl = 4200 Дж/(кг• К), aT = 1,7 •Ю-4 Н/(м• K), Rk = Hк = 5 см. Газ — воздух, температура и давление на удаленном расстоянии от подложки Tg = 293 K, pg=103 Pa, коэффициенты переноса в газе определяются по формулам, полученным из распределения Максвелла. Температура подложки Ts = 308 K. В момент t = 0 температура жидкости и газа одинакова и равна Tg , температура подложки – Ts , скорости равны нулю.

Обсуждение результатов

Разность температур между подложкой и газовой средой приводит к неоднородному распределению температур на поверхности капли. Связанный с температурой градиент поверхностного натяжения является движущей силой конвекции Марангони. Это явление существенно для небольших капель, так как в малых объемах гравитационные эффекты пренебрежимо малы. Обычно в численных расчетах конвективный поток тепла от поверхности жидкости описывается посредством числа Био (Biot). Однако в [11] было показано, что это приближение может существенно повлиять на результат из-за неточностей определения самого числа Био. В настоящей работе тепловой поток от поверхности описывается уравнениями (3), (6), что дает возможность получить более точное описание процесса теплообмена. Кроме того, в численных исследованиях динамики капли предполагают, что конвекция Марангони не изменяет форму капли, т.е. профиль капли остается равновесным, какие бы течения в жидкости не возникали [4–6]. Вопрос о возможных перемещениях межфазной границы, насколько нам известно, никем не поднимался, хотя это кажется важным, например, для измерений поверхностного натяжения методом большой лежащей капли.

Как показали расчеты, гравитационная конвекция в жидкости в рассмотренных условиях не развивается. Это связано с малой разностью температур между подложкой и вершиной капли – в указанных выше условиях она составляет ~0,2 К. Однако этой разницы температур достаточно для развития конвекции Марангони.

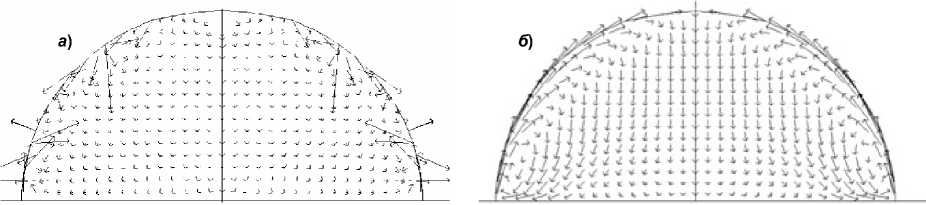
Рис. 2. Конвекция Марангони в осевом сечении капли: а ) начальная стадия; б ) установивший вихрь

В поведении жидкости и газа можно выделить две стадии.

• 1)    В жидкости вблизи поверхности образуется несколько малых вихрей. Формирование первого такого вихря начинается вблизи подложки и затем охватывает всю приповерхностную область (рис. 2, а ). Скорости в жидкости при этом меняются быстро как по величине, так и по направлению. В это время в газе формируется течение, направленное вниз, в горячую область с малой плотностью, из-за чего плотность в нижней части повышается и появляется обратное тече-

• Физика

ние. Возникают быстро затухающие течения воздуха, в которых скорости направлены то вверх, то вниз всюду, кроме области, где они огибают каплю.

• 2)    Течения в газе затухают, причем установившееся давление имеет распределение Больцмана вдоль оси z . Вихри в капле сливаются в один большой вихрь, жидкость в котором движется вдоль поверхности капли вверх и вниз вдоль оси в объеме (рис. 2, б ). В отсутствие испарения такой вихрь существует все время, пока поддерживается постоянной разность температур между подложкой и газовой средой. Такое же поведение жидкости в капле наблюдалось в [6].

Как выяснилось из расчетов, интенсивное движение внутри капли может нарушить ее равно- весную форму. На рис. 3 показана временная зависимость отклонения высоты капли от равновесной. Как видно из рисунка, эта зависимость представляет собой затухающие колебания, причем сравнение с результатами [7] указывает на возбуждение основной моды колебаний лежащей капли. Таким образом, поверхность лежащей капли при нарушении термодинамического равновесия совершает затухающие механические колебания. Амплитуда колебаний зависит от разности температур подложка–газ и может составлять несколько микронов. Колебания быстро затухают, и уже по истечении 0,1 с после начала процесса форму каплю можно считать равновесной.

ЛН(мкм)

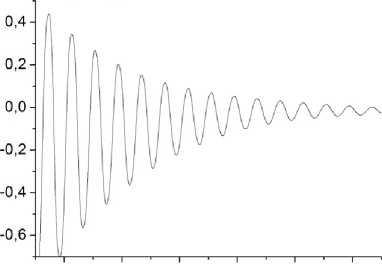
0,01   0,02   0,03   0,04   0,05   0,06 ^с)

Рис. 3. Временная зависимость отклонения высоты капли от ее значения в равновесии

Заключение

Таким образом, в работе проведено численное исследование динамики поведения лежащей капли и проанализирована эволюция формы капли при нарушении термодинамического равновесия в системе подложка–капля–газ. Неравновесное состояние таково, что температура подложки поддерживается большей температуры газа в удалении от капли. Внутри капли, лежащей на нагретой подложке, возникает вихрь конвекции Марангони, скорости в котором направлены вверх в узкой области вдоль поверхности и вниз во всем остальном объеме.

Численные расчеты показали, что на начальной стадии процесса возникают свободные колебания поверхности капли, частота которых совпадает с частотой основной моды. После затухания колебаний профиль капли остается равновесным, определяемым уравнением Лапласа. Длительность переходного интервала зависит от вязкости жидкости и для капли воды массой 0,525 мг составляет 0,1 с. Интервал установления равновесного профиля этой капли, таким образом, мал, и не может повлиять на точность измерения поверхностного натяжения методом лежащей капли.