Численное исследование процесса разрушения ледяного покрова с учетом сжимаемости и неоднородности

Механическое поведение ледяного покрова под действием различных нагрузок представляет значительный прикладной интерес при проектировании нефтегазодобывающих платформ, при проведении мероприятий по предупреждению ледяных заторов на реках, в целях продления навигации в водоемах. Натурные эксперименты с ледяным покровом требуют больших материальных затрат, в связи с чем важную роль приобретает численное моделирование с применением современных вычислительных средств. За последнее десятилетие построением математических моделей, адекватно описывающих механическое поведение ледяного покрова, занимался ряд исследователей [1–5], в числе которых и авторы настоящей статьи.

Так, в работе [1] предложена феноменологическая модель механического поведения льда при больших скоростях деформаций. Модель позволяет учитывать такие явления как образование трещин, различие предела прочности при растяжении и сжатии, возможность возникновения в раздробленном льду гидростатического давления и ряд других. Сравнение вычисленных и экспериментальных данных показало качественное и количественное совпадение результатов для многих условий.

Модель разрушения льда при большой площади силового контакта построена в работе [2] на основе анализа натурных показателей. Модель способна качественно объяснить характер разрушения при взаимодействии ледовых образований с морскими платформами. Более подробный обзор исследований в области механики ледяного покрова представлен в [3, 4].

Работы [5–7] посвящены математическому моделированию процесса разрушения ледяного покрова с помощью разработанных для этих целей устройств [8, 9]. В основе устройств лежит локализация процесса горения газовоздушной смеси в замкнутом объеме. Для построения математической модели ледяного покрова в работах использовались следующие основные допущения: лед считался линейноупругим несжимаемым изотропным однородным телом, а деформации в нем — малыми. Следует отметить, что допущения о линейной упругости и изотропности льда традиционны и применяются при решении задач, где исследуется такой материал, а обоснованность допущений подтверждается экспериментами. Утверждение, что лед есть однородная и несжимаемая среда, является не столь однозначным и может вызвать закономерные вопросы. Во-первых, любая среда, в той или иной степени, является сжимаемой; в частности, для ледяного покрова коэффициент Пуассона по разным данным составляет примерно 0,35, в то время как для гипотетического несжимаемого материала он равен 0,5. Во-вторых, ледяной покров, существующий в естественных условиях, характеризуется значительным перепадом температур на нижней и верхней поверхностях, способным, вообще говоря, привести к заметной пространственной неоднородности физико-механических свойств льда. В данной работе

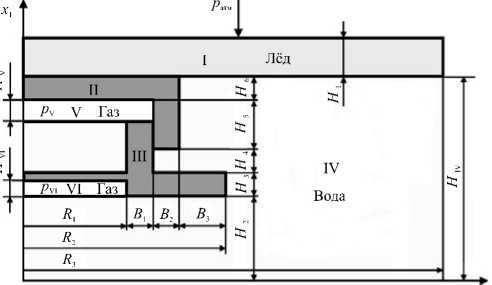
Рис. 1. Расчетная схема

исследуется влияние сжимаемости и неоднородности ледяного покрова на результаты численного моделирования его разрушения с помощью новых способов создания нагружающего воздействия [8, 9].

• 2.    Постановка задачи

• 2.1.    Области I–III

Расчетная схема для задачи разрушения льда с помощью устройства, описанного в [8], приведена на рисунке 1. Здесь: I — ледяной покров, II, III — цилиндры, IV — вода, V, VI — газовоздушные подушки. Данная расчетная схема аналогична схеме из работы [7]. Рассмотрим подробно основные допущения, использующиеся для построения математической модели.

Среды в этих областях положим линейно упругими сжимаемыми изотропными. При этом будем учитывать неоднородность по толщине физико-механических свойств ледяного покрова (область I), а материалы металлических цилиндров (области II, III) для простоты примем однородными. Деформации, возникающие в областях I ^ III, будем считать малыми. Таким образом, напряженно-деформированное состояние в этих областях математически описывают:

– уравнения движения

I д V.         д V. ।

^с у ,j ⁺ F i = I i , I ,- =р J    -^{+ V} k   -1 ( i , j , ^k = 1,2,3);

(дт     д x_k )

– закон Гука для изотропного материала

»₈ - а5.=2 G, ( x 1 ) ( 8 ij - s5 ij /3 ) ( i = 1, 2, 3);

– уравнение неразрывности

• 3    Kd2 -& = 0. d т д x i

Здесь: t — идентификатор области, t = I, II, III; c _iy , Б _у — компоненты тензоров напряжений и деформаций соответственно; F_i ^t — проекции удельной объемной силы на координатные оси x_i ( i = 1, 2, 3); p _t — плотность материала; v i — проекции скоростей перемещений на координатные оси x i ; т — время; ст — гидростатическое напряжение; G_t ( х 1 ) — модуль сдвига в области t как функция вертикальной координаты х 1 ; б — первый инвариант тензора деформаций, б = б ii ; 8 _у — символы Кронекера; в уравнениях (1)–(3) производится суммирование по повторяющимся индексам; K — коэффициент объемного сжатия, который выражается через модуль сдвига G и коэффициент Пуассона v следующим образом: K = ( 1 - 2 v)/ ( 2 G ( 1 + v ) ) .

В случае малых деформаций справедливы соотношения:

d б „

-у = ^у ^ ^Бу = J^ ij ^{d т} , d т                  "Г

где [ ^ _у ] — тензор скоростей деформаций, ^ _у = ( v i , _у + v j , i ) /2 . При дискретном по времени (с шагом Ат m ) процессе деформации, когда т = ^ Ат m , формула (4) имеет вид: m

(s.) =Y(L.) At = (s ) ,+(£. ) At ,

ij m       j^m mm ij m -1      ij m m ,

m где Атm — продолжительность m-го временного шага; (^ij)m и (eij.)m — компоненты тензоров скоростей деформаций и деформаций на m-м временном шаге; (eij)m-1 — компоненты тензора деформаций на (m -1 )-м временном шаге

Рассмотрим подробно связь модуля сдвига G t с координатой x_i в областях t = I - III. Поскольку материалы цилиндров, согласно модели, однородны, то модули при t = II, III представляют собой константы: G t ( x 1 ) = G_t . Ледяной покров ( t = I ) , как сказано выше, считается неоднородным. Прежде чем говорить о конкретном модуле сдвига льда, необходимо отметить то обстоятельство, что физикомеханические свойства естественного ледяного покрова имеют существенную как пространственную (не только по толщине), так и временную неоднородность. Заметно отличаются между собой по характеристикам лед речной и морской, однолетний и многолетний, арктический и антарктический, лед в период нарастания и таяния и так далее. Разумеется, учесть все многообразие видов ледяного покрова невозможно, однако рассматривать отдельно морской и пресноводный лед, безусловно, необходимо: именно между ними имеются наибольшие различия. Морской лед — это среда, в которую, кроме непосредственно льда, входят твердые соли (при достаточно низких температурах), солевой раствор, пузырьки воздуха и другие неорганические и органические примеси. Пресноводный лед более однороден по своему составу, и большую часть примесей в нем составляют пузырьки воздуха. Морской лед податливый и вязкий, а пресноводный — жесткий и хрупкий.

Для морского льда будем учитывать неоднородность модуля Юнга только по толщине; коэффициент Пуассона и плотность примем постоянными. Модуль Юнга традиционно [12] считается зависящим только от объема солевого раствора V b : Е = Е ( V b ) . Объем солевого раствора V b , в свою очередь, определяется соленостью льда и температурой: V b = V b ( S , T ) , а соленость и температура льда являются функциями вертикальной координаты x _i: S = S ( x 1 ) , T = T ( х 1 ) . Учитывая все вышесказанное, а также известное соотношение теории упругости G = Е /( 2 + 2 v ) , получаем:

G i ( x i ) = E i ( V b ( S ( x i ) , T ( x i ) ))/ ( 2 + 2 v i ) .

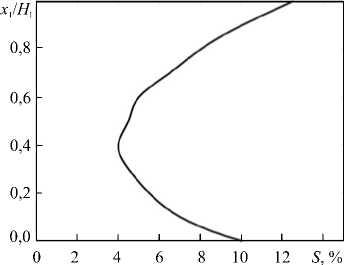
Рис. 2. Профиль солености морского ледяного покрова

Функцию связи температуры льда T и вертикальной координаты x ₁ для простоты возьмем линейной, изменяющейся от температуры плавления льда T_melt на нижней поверхности ледяного покрова до температуры окружающей среды T _min на верхней. Профиль солености ледяного покрова не постоянен и непрерывно меняется под действием различных процессов, происходящих во льду. В данной работе используется «С-образный» профиль солености, характерный для однолетнего льда морей Арктики и Антарктики в период нарастания [10]. Профиль изображен на рисунке 2.

Соотношение для вычисления объема солевого раствора Vb (S, T) (в промилле) как функции солености S (в промилле) и температуры T (в ºС) получено на основе экспериментальных данных в работе [11] и имеет вид:

V b = S ( 49,i85/1 T + 0,532 ) .

Данная формула справедлива для интервала температур от –22,9 до –0,5°C.

Модуль Юнга морского льда зависит от относительного объема солевого раствора V_b следующим образом [12]:

Ei = Ef (i — Vb) , где Ef — модуль Юнга пресноводного льда (в ГПа).

С учетом (7), (8) выражение для модуля сдвига льда (6) принимает следующий вид:

(

G 1 ( X 1 ) = E f 1 - X ( X ) П9Н, V VI T ^{( x} , )

T)4

+ 0,532

))

^2 + 2 v ) .

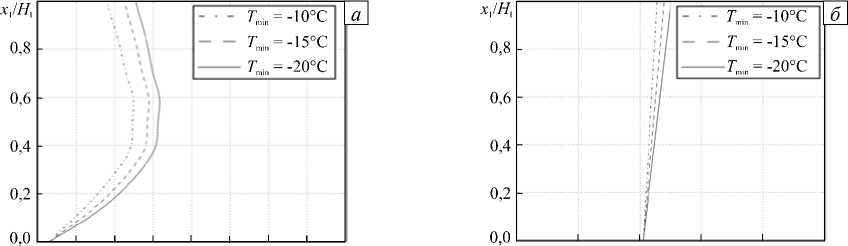
На рисунке 3, а приведено распределение модуля сдвига по толщине морского ледяного покрова для трех значений температуры T mn =- 10; - 15; -20°С, полученное с помощью формулы (9) с учетом профиля солености (Рис. 2) при E_f = 9 ГПа. Для пресноводного льда будем учитывать зависимость модуля Юнга только от температуры T : E = E ( T ) . Профиль температуры имеет, как и ранее, вид линейной функции, изменяющейся от T_melt на нижней поверхности до температуры окружающей среды T _min на верхней границе. В итоге модуль Юнга имеет вид [13]: E ( T ) = E ₀ + e(T melt - T ). Тогда модуль сдвига можно определить по формуле:

• G , ( х , ) = ( E о + e ( T_meh - T ) )/( 2 + 2 v ) , (10)

где E ₀ = 9 ГПа — модуль Юнга при температуре плавления, e = 4,5 - 10 ³ ГПа/К. Полученные профили показаны на рисунке 3, б .

Также для сравнения результатов использовалась однородная модель морского льда:

G ( х ) = E 0 /( 2 + 2 v ) .

0,0 0,5 1,0 1,5 2,0 2,5 3,0 G, ГПа                       3,0     3,2      3,4     3,6   3,8 G, ГПа

Рис. 3. Профиль модуля сдвига морского ( а ) и пресноводного ( б ) ледяного покрова

• 2.2.    Область IV

2.3.    Области V и VI (газовоздушная смесь)

• 2.4.    Единая система уравнений для областей I–IV

Заполняющая эту область вода моделируется как ньютоновская вязкая несжимаемая жидкость. Система дифференциальных уравнений для воды, по сравнению с предыдущими работами [5–7], не претерпевает каких-либо изменений:

F-Ip + ЦV2 v = I*,   It = p 11 Vi+ Vk ^l   (i, k = 1, 2, 3), t = IV;(12)

dXi                           V v^ 0,(13)

где p — давление; ц — коэффициент динамической вязкости; V ² — оператор Лапласа.

Процесс горения в областях V, VI моделируется по аналогии с работами [5–7]. Давления p_V и p_VI продуктов сгорания возрастают от начального значения (давления, создаваемого при нагнетании газовоздушной смеси) p ₀ , до некоторого конечного p ₁ . Процесс горения полагается адиабатическим; для продуктов горения выполняется закон pV = const. Для задания величины р 1 используются экспериментальные данные [14].

Системы уравнений (1)–(3) и (12)–(13) можно привести к единому виду:

,    1 - it 71 _ I ⁸v. ,      ⁵ v.

G ,- + Fj = I , I — P      + Vj- ---

*j ^, j             ‘         ' t (dr k d xk

,

t — I - IV;

^G j ^-G $ у ^{— 2 X} C t ,

|X t — G t ( X ) , C — ^ j -sS _y /3, ^X _t ^— ц , C j ^— ^ у ,

I ,         1 - 2 v _t

3 K t ( X ) f-f — 0, f t ⁽ x ^)— 2 G t ( x i )( 1 +v t ) d т  d x

-          [ K t ( X i ) — 0 ,

t — I - III;

t — IV;

t — I - III;

t — IV.

• 2.5.    Начальные и граничные условия

В начальный момент времени во всей расчетной области скорости перемещений и скорости деформаций равнялись нулю:

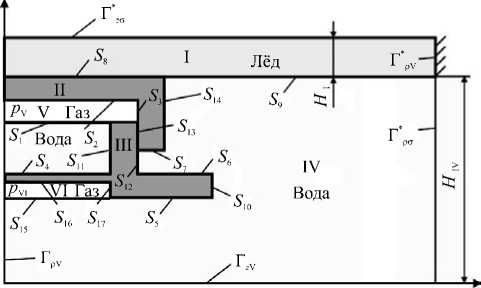
P

Рис. 4. Граничные условия задачи

v - — 0, ^ — 0 ( - , j — 1,2,3 ) .   (17)

Задача решалась в цилиндрической системе координат с учетом осевой симметрии

Ф , z^Z ф      , -pn      ,       z ф       РФ , и имела граничные условия (Рис. 4):

– на оси симметрии

Vp|r — 0,   "pzlr — 0,( p Vp

Gzz|r- — -Patm ;

Z G

– условия на поверхностях контакта разнородных сред:

Gpz|s — 0 (- — 3,10-14,17),(21)

gzp ( — 0 (- —1,2,4 - 9,15,16);(22)

– давление продуктов горения газовоздушной смеси в областях V и VI:

Gzz Is, — -PV (i — 1,2), Gpp 1^ — -PVI,

Gzz\sv — -PV(i — 15, 16), Gpp |S7 — -PVI;

– условие непротекания на дне водоема:

Vz |r — 0;(25)

zv

– условия на внешней границе расчетной области:

Vp |r.v — 0,       Gpz |^ — -VGX viP /I V„ I ,

Gpp|r. — -P1 - Y1HI -Y2h    (0 < h < HIV),(27)

• ¹    pg

• 3.    Численная схема и алгоритм решения

где vsli — скорость скольжения области I относительно некоторой основы, v , = v   - v* (здесь: v* — s“p                                                                                                                                                s-p       z |rzv      z                    z скорость основы, и если она неподвижна, как в рассматриваемом случае, то v* = 0; | vu | — нормирующая скорость); стs — условный предел текучести льда; v — коэффициент трения (принимался v = 1000).

Наряду с моделью (14)-(16) для сравнения результатов расчетов далее будет использоваться модель из работ [5-7], основанная на предположении о несжимаемости и однородности упругих сред в областях I, II.

Для решения начально-краевой задачи (14)-(27) применим незначительным образом модифицированную численную схему, опубликованную в работе [7], и обсудим привнесенные отличия.

Запишем уравнение неразрывности (16) в конечных разностях для ортогонального цилиндрического элемента с учетом осевой симметрии с помощью полностью неявной схемы в соответствии с работой [7]. Для наглядности вместо длин дуг S j будем использовать размеры элемента A z , Ар :

3 K t ( z )

И m -И m -1 + v (А2) ^At m       z ^A z

^(Act) p 1 ^A v z ^{A v} р      ^v р

-------

Ap I A z Ap p 1 + p ₂

где ( ст ) m — гидростатическое давление на временном шаге m ; v z , v _p — средние по элементу скорости в направлении z и р, зафиксированные на к -й итерации; ( Act ) z , ( Act )_p — изменение гидростатического давления вдоль соответствующей координаты на текущем временном шаге m ; At _m — продолжительность временного шага m ; A v z = v z - v z , A v _p = v / - v p , v_z = v 1 + v z ; v _p = v 1 + v / ; v z , v p — скорости на i -й грани элемента в направлении z и р; A z , Ap — размеры ортогонального элемента в цилиндрической системе координат, p 1 , p ₂ — радиусы кривизны внутренней и внешней граней элемента.

Приведем уравнение (28) к рекуррентному виду:

2     1    A z / 2     1 \        A z     / 1      ₂

vz = ^v z -тЧ ^v p - ^v p ) ^-— -^{( v} P ^{+ v} p ) ^{+ 3} K t ⁽ z ) ^{Ap           p}1 ^{+ p}2

^A z ( ^(СТ) m ^-(CT) m - 1 ) = /. X --------------------⁺ v z ^(Act)

At

m

z

—v ( Act ) . Ap ^{p V} ’^p

Соотношение (29) позволяет вычислить скорости v_z , при этом расчет производится в направлении возрастания координаты z . Конечно-разностная форма уравнений движения (14) останется неизменной [7]. Для раскрытия нелинейности применяется та же итерационная процедура, что и в работе [7]. При этом нелинейные члены присутствуют не только в уравнениях движения (14), но и в уравнении неразрывности (16), что обусловлено наличием в нем полной производной d ст/ d т .

Общее число независимых переменных образует множество следующего вида:

X {[СТ zzl Го ] , [ vpl Г,ст] , [ vz Г ст] , [ vp] , [CTppl Г* v ] , [ v pl Г*ст] , И=I,II,III } , где Г , Г* ., Г\ „, Г* . — поверхности, ограничивающие рассматриваемую расчетную область; plp=0       p lp=p        z lz=0       z \z=z

Гpv, Гp*v, ГpCT, Гp*CT, Гzv, Гzv, Гzст, Г*ст — поверхности, где заданы скорости перемещений v и нормальные напряжения. По сравнению с работой [7] множество стало шире за счет добавления группы неизвестных [ст]     , обусловленных сжимаемостью упругих сред. Этой группе соответствуют новые уравнения, имеющие место для каждого элемента расчетной сетки в областях I-III:

Faf =(ctzz)f +(CTpp)f + (ctw)f -3(ct)f = 0 (f = 1,..., f,), где f, — количество элементов в областях t = I, II, III.

Для решения задачи используется алгоритм, разработанный в [7].

• 4.    Результаты численных расчетов

  Физико-механические параметры льда, материалов цилиндров и воды были взяты из работ [8, 15, 16] и равнялись: удельный вес у , = 9200 Н/м³, Y ₂ = y ₃ = 78000 Н/м³; модуль сдвига G ₂ = G ₃ = 8 ■ 10 ⁴ МПа; динамическая вязкость ц = 1,789 мПа^с.

Начальные геометрические параметры имели следующие значения (см. Рис.1): H I = 1 м; H ₂ = 10 м; H ₃ = 0,1 м; H ₄ = 0,4 м; H ₅ = 0,5 м; H ₆ = 0,1 м; H V = 0,05 м; H V, = 0,04 м; R 1 = 2,5 м; B 1 = 0,1 м; B ₂ = 0,1 м; B ₃ = 0,3 м; R ₃ = 20м. Конечное давление р 1 в замкнутом объеме составляло р 1 ® 0,7 МПа [14].

Исследуемый процесс разбивался на равные по длительности шаги по времени. Для анализа сходимости применяемого вычислительного алгоритма и определения оптимального разбиения области проведена серия тестовых расчетов на сетках, состоящих из 5668, 7316, 10540, 13195 и 14214 элементов. Под оптимальной понимается сетка, дальнейшее измельчение которой не приоводит к существенному изменению результатов. Расчеты дали одинаковую качественную картину напряженно-деформированного состояния в системе «лед-разрушающее устройство» на всех сетках; количественная разница в результатах с использованием сеток из 10540, 13195 и 14214 элементов составила 1 ^ 2%. В итоге за основную была выбрана сетка из 13195 элементов, из которых 2900 приходилось на ледяной покров. Именно при этой сетке были получены все нижеприведенные результаты.

Необходимо отметить, что дополнительные нелинейные члены в уравнении (16) не оказали принципиального влияния на сходимость итерационной процедуры раскрытия нелинейности, и 5 ^ 8 итераций оказались достаточными для получения максимальной относительной разницы e = 0,001 между полями скоростей на соседних итерациях.

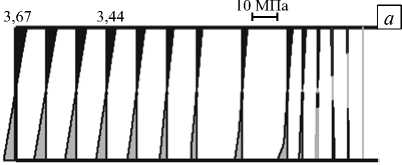
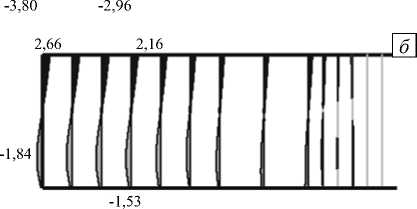
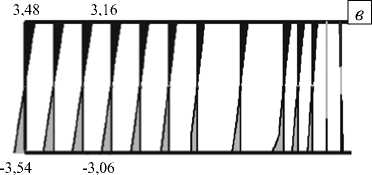
Рис. 5. Эпюры напряжений О рр в момент времени т = 0,04 с в пресноводном ( а ), морском ( б ) и однородном морском ( в ) ледяном покрове

На рисунке 5 приведены результаты решения начальной краевой задачи (14)-(27) в виде эпюр напряжений о_рр в момент т = 0,04 с (то есть в конце процесса разрушения) при зависимостях модуля сдвига от вертикальной координаты (9), (10) и (11). Из рисунка видно, что во всех трех случаях наблюдается схожая картина: под действием верхнего цилиндра в зоне радиусом R <  R 1 ледяной покров изгибается, в результате чего его нижние слои сжимаются, а верхние растягиваются. Вне области действия верхнего цилиндра напряжения во льду меняют знак и быстро убывают по абсолютной величине (практически падают до нуля). Напряженно-деформированнные состояния пресноводного и однородного ледяного покровов (Рис. 5, а , в ) отличаются незначительно: и в том и в другом случае напряжения в области R <  R 1 распределены по толще льда линейно (с минимумом на нижней поверхности и максимумом на верхней), а различия есть только в числовых значениях (примерно 5%). Для морского ледяного покрова (Рис. 5, б ) характерна иная картина. Во-первых, напряжения в толще льда распределены нелинейно (максимум на верхней поверхности, минимум на расстоянии ® 0,25 H I от нижней поверхности), что можно объяснить существенной неоднородностью свойств морского ледяного покрова (Рис. 3). И, во-вторых, между значениями напряжений в морском и однородном льду имеет место существенная разница, достигающая 50 %.

На рисунке 6 показаны эпюры напряжений о_рр при т = 0,04 с для морского (Рис. 6, а , б ) и пресноводного (Рис. 6, в , г ) льда соответственно, при этом буквами ( а ) и ( в ) обозначены результаты,

Рис. 6. Эпюры напряжений σ_ρρ при τ= 0,04 с

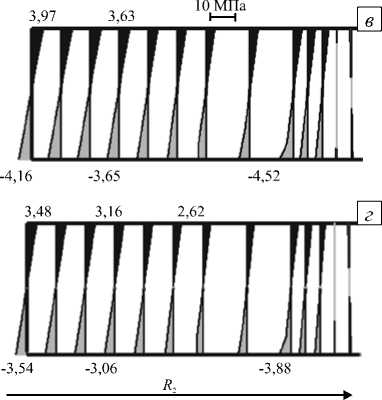
полученные для модели из работ [5–7], в которой упругие среды приняты несжимаемыми, а буквами (б) и (г) — для модели (14)–(16) с учетом сжимаемости упругих сред. Видно, что качественная картина напряжений как в морском, так и пресноводном льду при учете сжимаемости сохраняется. При этом числовые значения напряжений по абсолютной величине меньше, чем в несжимаемом ледяном покрове, примерно на 10–15%. Все вышесказанное справедливо не только для последнего момента времени τ=0,04 с, но и для всего процесса в целом. Разумеется, значения напряжений на разных временных шагах отличаются между собой.

4 м

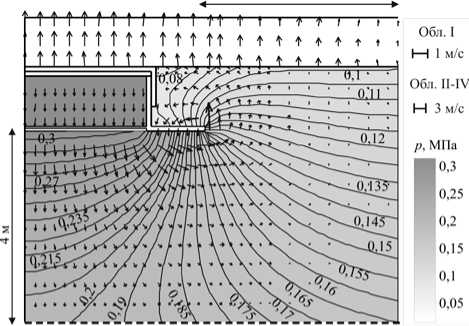
Рис. 7. Векторное поле скоростей и изолинии давления в окрестности устройства в момент времени τ= 0,04 с

Следует отметить, что учет сжимаемости и неоднородности упругих сред практически не сказывается на остальных компонентах системы. Так, характерная картина течения воды в окрестности устройства в ходе процесса не зависит от используемой модели ледяного покрова и приведена на рисунке 7 для момента времени τ= 0,04 с. При рассмотрении конструкции сбоку можно увидеть область (в пространстве между ледяным покровом и нижним цилиндром), в которой в результате разнонаправленного движения цилиндров образуется область пониженного давления. В свою очередь под нижним цилиндром возникает область повышенного давления. Максимальная скорость движения воды имеет место рядом с боковой поверхностью нижнего цилиндра S ₁₀. В той части расчетной области, которая

не изображена на рисунке 7, скорости движения на порядок меньше, а распределение давления близко

к гидростатическому.

Во всех полученных результатах можно выделить ряд закономерностей. Во-первых, касательные напряжения, возникающие во льду и устройстве, на порядок меньше нормальных, из чего можно сделать вывод, что главные напряжения близки к нормальным. Во-вторых, напряжения σ_ρρ и σ_ϕϕ отличаются незначительно. В-третьих, изменение температуры верхней поверхности ледяного покрова практически не влияет на уровень значений вычисляемых величин.

• 5.    Заключение

Суммируя все вышесказанное можно сказать следующее:

• 1)    Учет неоднородности имеет существенное значение только для морского льда; пресноводный ледяной покров можно принимать однородным по толщине.

• 2)    Модель (14)–(16), учитывающая сжимаемость упругих сред, безусловно более полно описывает исследуемый процесс. Характерная картина напряженно-деформированного состояния упругих компонент ( t = I - III) расчетной области при учете сжимаемости не меняется. Разницу в вычисленных значениях

(20–25% в элементах устройства, 10–15% в ледяном покрове) можно считать несущественной. Это объясняется следующими причинами. Во-первых, при анализе напряжений в устройстве основной интерес представляет распределение напряжений и их максимальное (минимальное) значение. Необходимо удостовериться, что напряжения в конструкции не превышают предела прочности на растяжение (сжатие) с некоторым коэффициентом запаса прочности. Существенно, что конкретные значения напряжений играют при этом второстепенную роль. Во-вторых, экспериментальные исследования механических характеристик естественного льда дают очень большой разброс результатов, который достигает десятков процентов, в сравнении с чем учет сжимаемости вносит относительную небольшой вклад (в 10–15%), и поэтому при моделировании процесса разрушения рассмотрение льда как несжимаемой среды можно считать достаточно адекватным приближением.

Это заключение можно отнести к более широкому классу задач определения напряженно-деформированного состояния ледяного покрова, в которых лед считается упругой средой, длительность нагружения не превышает нескольких секунд, а скорость деформации во льду соответствует скорости исследуемого процесса (10 -5 ^ 10 2 с^-1).

Следует отметить, что ранее сжимаемость льда исследовалась в работе [17], в которой сделан вывод о допустимости подхода ко льду как к несжимаемой среде во многих случаях. Но это относится лишь к пресноводному льду при очень низких температурах. Вывод, полученный в настоящей работе, распространяется и на пресноводный, и на морской лед в широком диапазоне температур.

• 3)    Учет сжимаемости упругих сред и неоднородности льда (модель (14)–(16)) не оказывает влияния на течение воды ( t = IV).

Работа выполнена при финансовой поддержке РФФИ (проект № 11-01-98500-р_восток_а).