Численное исследование процессов в моделях Хоффа

Пусть Q C R" - ограниченная область с границей УП класса С°°. Уравнение Хоффа (А + Д)щ = аци + а^и³ + ... + а₈и?⁸"~^г                       (1)

в случае п = 1 моделирует динамику выпучивания двутавровой балки [1], где параметр A G R+ характеризуют нагрузку на балку, т. е. сжимающую силу, которая принимается нами как величина постоянная, а параметры a, G R (oj • aj > 0 Vi, j) характеризуют свойства материала балки. Под прямой задачей понимается начально-краевая задача

(А + Д)(п(ж,0) — mq(t)) = 0, ж £ Q, и(жД) = О, (ж,£) € 5Q х R,           (2)

где искомая функция и = u^x,t\ х £ Q, t £ R, имеет физический смысл отклонения балки от вертикали, т.е. от положения равновесия.

Под обратной задачей понимается задача нахождения не только решения уравнения (1), но и параметров а, для того, чтобы узнать различия между имеющимся материалом балки и предполагаемым. Для решения обратной задачи вводятся дополнительные условия т'-'^агио^) + а2По(ж) + ... + otsU^^^x^dx = щ, » = 1,2,              (3)

характеризующие моменты изменения скорости динамики выпучивания балки. Нашей целью является качественное и численное исследование разрешимости прямой и обратной задач (1) - (3) при различных значениях параметров. Качественное исследование задачи

• (1 ) - (2) облегчается тем обстоятельством, что она в подходящим образом подобранных банаховых пространствах 11 и S редуцируется к задаче Шоуолтера-Сидорова

Z(u(0) - tzq) = 0,                                      (4)

для полулинейного уравнения Соболевского типа

Lu = Mu + N(u).                            (5)

Статья кроме вводной части и списка литературы состоит из двух параграфов. Первый параграф содержит сведения о качественном исследовании, а второй параграф посвящен численному исследованию прямой и обратной задач (1) - (3). Все доказательства первого параграфа проведены с использованием подходов, изложенных в [2] - [4].

1.    Прямая и обратная задачи

Для редукции задачи (1) - (2) к задаче Шоуолтера - Сидорова для абстрактного полули-0 1

нейного уравнения Соболевского типа зададим пространства И =Шз, 5 — W₂ и операторы

Г                                   °1

(Lu, г) = (Xuv — VuVv)c/a;, Vu,v EW2,

Q

^Ми,^ = ai J uvdx, (A(u),v) = J(ot^u³ + ■•■-V a_su^2s-1^vdx Уи^еЬ^И).

Пространство S сопряжено к Н относительно скалярного произведения (•,■) из L2. Операторы L,M Е £(11; 5ф причем оператор L фредгольмов. Спектр оператора L вещественен, дискретен, конечнократен и сгущается только к точке —ос.

Обозначим через {А^} занумерованные по невозрастанию множество собственных значений однородной задачи Дирихле для оператора Лапласа, а через {(/дф-ортонормированное в смысле L2 множество соответствующих собственных функций.

Напомним, что оператор М называется (L, 0)-ограниченным, если

За > 0 Уд G С (\ц\ Xi'Hip-G PLW = {ц Е С : (цЬ - М^ £ ЦМ и при этом бесконечность является устранимой особой точкой L резольвенты оператора М.

Лемма 1. При, всех а у Е R\{0}, А Е R оператор М (L, (^-ограничен.

Лемма 2. Оператор N Е С°° (Н; S) ■

Вектор-функцию и Е С¹((— г, г); 11), удовлетворяющую уравнению (5) при некотором т Е R+, назовем решением этого уравнения, а если решение вдобавок удовлетворяет условию (4), то будем называть его решением задачи (4), (5).

Если kerL = {0}, то уравнение (5) тривиально редуцируется к эквивалентному ему уравнению й = F^                          (6)

где оператор F = LT^M + N) Е С°°(11) по построению. Существование единственного локального решения и Е С^г((—т, т);П) задачи (4), (5) при любом uq G 11 — результат классической теоремы Коши. Другое дело, если kerb / {0}. В этом случае полезным оказывается следующее понятие.

Определение 1. Множество ф С Н навивается фазовым пространством уравнения (5), если

• (г)    любое решение и = u(t) уравнения (5) лежит в ф как траектория, т.е. u(t) € ф t € (т,т);

• (и)    при любом м₀ € Ф существует единственное решение уравнения (5), удовлетворяющего условию Коши

н(0) = ио-                                         (7)

Поскольку решение задачи (6), (7) в случае kerZ = {0} является решением задачи (5), (7) (и наоборот), то фазовым пространством уравнения (5) в данном случае служит все пространство £1. Рассмотрим случай, когда 0 Е Построим множество

9Л = <  и Е £1 : («1 + «г^² + ■•■ + а₈и^28-х^шркйж = 0, k = 1,..., т

Теорема 1. Пусти cq Е W\{0} - одного знака, п < 2 при s Е N или п < 3 при s = 3 или п < 4 при з = 2 и

• (г)    ker L = {0}. Тогда фазовым пространством уравнения (1) служит все пространство £1.

• (ii ) ker L ^ {0}. Тогда фазовым пространством уравнения (1) служит простое многообразие 9Л.

Теорема 2. При любых oq Е 1$\{0} - одного знака, п < 2 при s € N или п < 3 при s = 3 или п < 4 при з = 2 и ио Е £1 задача (1) - (3) имеет единственное решение.

Перейдем к исследованию обратной задачи. Система (3) имеет решение в том и только том случае, когда определитель системы

5 =	J uo^dx п №)ds Q	фxuo(x)dx п Jxu^x^dx Q	J x^uo^dx    . n J x2UQ(x)dx     . Q	..    J x2s 2uo^dx ..    J х2®-2иу(х^х n	^0.
		J xuQS~1(x)dx	J х2иу8-1(х^х .	. J x2s-2Uq8-1 (x'idx
	Q	Q	n

Коэффициенты cq определены формулами oq = 5i • 5 ¹, где

5i- J uo^dx n Ju^dx J xuo^dx n Jxuy(x)dx Q J x2uo(x)dx     . J x2Uy(x)dx     . •■ Pl    ■ ■ • М2 - ..     J x2s-2uo^x^dx Q ..     J x2s-2Uo(x)dx n j ui^H^w J xUgS~1(x)dx J x2Uq8-1 (,x)dx . • Ps • . J x2s-2Uo8-1 ^dx n n Q причем cq Е R\{0), когда ^ ^ 0. В случае тривиального ядра оператора L при производной по времени справедлива следующая лемма.

Лемма 3. Пусти 0 ^ cr(Z), п < 2 при s Е N, или п < 3 при s = 3, или п < 4 при s = 2 и д^ ^ 0 при г = 1,..., s. Тогда для любого uq Е &, pi Е И. и некоторого Т = Т(ио^ существует единственное решение и Е С^г((—Т,ТуМу cq € К\{0} задачи (1) - (3).

В случае нетривиального ядра оператора L при производной по времени для нахождения условий существования и единственности решения задачи (1) - (3) вводится множество Т) - множество допустимых значений pt, при которых решениями задачи будут коэффициенты «г одного знака. Искомое множество 3) имеет вид

D = {щ,щ € R : 61¹ §j > 0 УгД = 1, ...,s} .

Теорема 3. Пусть О G а^Ъ\ п < 2 при s€N, или п < 3 при s = 3, или п < 4 при s = 2 и 6i / 0 при г = 1,..., s. Тогда при любых р,;, ЕТ) и uq €11 существует единственное решение uECHWW «г € R\{0}, «г ■ «j - одного знака, обратной задачи (1) - (3).

2.    Численные эксперименты

На основе теоретических результатов для подтверждения простоты фазового пространства и разрешимости обратной задачи для уравнения Хоффа в системе компьютерной математики Maple 12.0. разработана программа, которая позволяет:

• 1.    По заданным коэффициентам а^А на основе метода Галеркина находить численное решение задачи Шоуолтера - Сидорова для уравнения Хоффа.

• 2.    По заданным коэффициентам д,,А на основе метода Галеркина находить численное решение обратной задачи для уравнения Хоффа.

• 3.    Получить графическое изображение этого приближенного решения, которое показывает простоту фазового пространства.

Для реализации вычислительных алгоритмов программы использовались встроенные функции и стандартные операторы языка программирования Maple 12.0. Для получения графического изображения подключен пакет plots.

В полосе (0, тг) х R рассмотрим уравнение Хоффа

Xut + Utx$ = ари + ayu? + ... + (XsU28(8)

начально-краевую адо) - wo) = о(9)

м(0Д) = п(тг, t) = 0, t € R(10)

и обратную 7Г

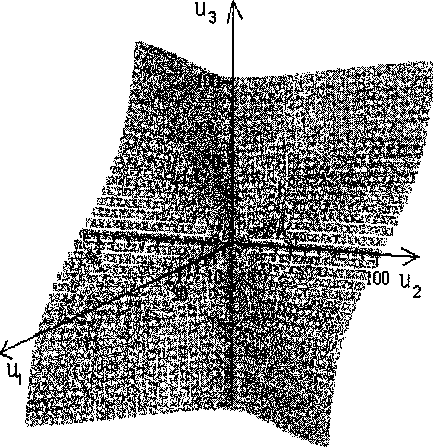
I xl-4avu,oU'} + cy

о задачи для него. Решение задачи (8) - (10) будем искать в виде галеркинской суммы т цта(^,т) = y^ufc(t)

fc=i где Урк) ~ ортонормированное в смысле L^(Отг) множество собственных функций, соответствующих собственным значениям Хк однородной задачи Дирихле для оператора ^ на (О,тг). Легко подсчитать, что <рк = Тк^ = ^/I'Sin^T), а А^ = —к2.

Пример 1. Требуется найти численное решение задачи (8) - (10) при заданных коэффициентах од = —1, «2 = —4, А = 1, т = 3 и з = 2.

Так как m = 3, то в силу (12) u(t,x) = i/2/7r(ui(t) sin ж + «2 (i) sin 2ж + us^t) зшЗт). В случае А = 1 условие теоремы 1 (и) выполняется, ввиду того, что 0 Е о-(ЬУ Умножив скалярно (8) на функции tpk, к = 1,2,3, получим систему дифференциальных уравнений

{12^1 (t^u^t) + 12uitou²to + 6^2 (<)пз(£) + 7rui(t) — би^^из^ + 6и³(£) = О,

—тгигМ + 3^u2to — 12п1(^)п2(<)из(0 — 12и2(£)иг(£) — би^) — 12u2(i)u2(t) = 0,   (13)

—6и|(£) — тгг^з(t) + 2u^(t) + 8тшз(£) — 6и1(£)и²(£) — 12u2(i)u3(t) ~ 12и²(£)из(£).

Результаты численного решения системы (13) частично приведены в таблице 1.

Таблица 1

Численное решение системы (13) с начальными условиями гц(0) = -0,00320384, и2(0) = 0,1, п3(0) = 0,2

t	^ito	«2 to	ИЗ (^
0	-0,320384е"2	ОД	0,2
0,1	-0,349083с-2	0,103985	0,202812
0,2	-0,380405е-2	0,108149	0,205677
0,3	-0,414593с-2	0,112503	0,208598
0,4	-0,451917с-2	0,117057	0,211576
0,5	-0,492667е-2	0,12182	0,214615
1	-0,760155е-2	0,149268	0,230805
2	-0,182643с-1	0,22978	0,269855
3	-0,443648с-1	0,375509	0,325156
4	-0,112723	0,725146	0,430126
4,8	-0,463326	3,874975	1,029568
4,84	-0,82426	9,744243	1,722825
4,847	-1,53129	27,978100	3,115508
4,8479	-3,044384	93,086718	6,125122

Пример 2. Требуется найти численное решение задачи (8) - (11) при А = 4, т = 3, s = 2, щ = 0,2, д₂ = 0,1, uoto) = — 1,5 ■ sins + 0,1 • sin 2s + 0,2 • sin3s.

Проверим выполнение условия теоремы 3: Si = —1,154361481, 5₂ = —0,6453391538, 5 = 0,1380486969, J / 0, 51 • 5г>0. Отсюда, «1 = —8,361987523, а₂ = —4,674721083. Результаты численного решения задачи (8) - (11) частично приведены в таблице 2.

Таблица 2

Численное решение обратной задачи (8) - (11) с начальными условиями ию = —1,5, м2о = 0,1, изо = 0,2

t	«ito	^(t)	из to
0	-1,5	0	0,2
ОД	-0,983011	0	0,304302
0,2	-0,679848	0	0,3940431
0,3	-0,478625	0	0,487207
0,4	-0,337134	0	0,593218
0,5	-0,234634	0	0,720378
1	-0,118496с-1	0	2,662645
1,12	-0,898515с-4	0	12,727984
1,126835	-4,688929с-13	0	3908,063397

Пример 3. Построить фазовое пространство уравнения (8) при заданных значениях т = 3 и s = 3, а\ = —0,052, «2 = — 1,97, аз = —3,73, А = 1 и А = 9.

фИ3

-о,go:

НИА-

-U.G04

-0.UC2

Фазовое пространство уравнения (8) при А = 1 и А = 9, если u(t,x) = T4i (t) -х/2/тг sin ж + и% (£) ^/2/тг sin 2т + из(^)д/2/я sin Зх

В заключение автор считает своим приятным долгом выразить свою искреннюю благодарность профессору Г.А. Свиридюку за постановку задачи и интерес к работе.