Численное исследование продольной компоненты электрического поля в электромагнитной волне

Волновое уравнение для электрического E ={Ex, Ey, Ez} и магнитного H = {Hx, Hy, Hz} полей в электромагнитной волне (ЭМВ) выводится из системы уравнений Максвелла на основании параксиального приближения д2Hz/дx2 » |kx дHz/дx|, здесь kx = 2^2 — составляющая волнового вектора k = {kx, 0, 0}, волна распространяется вдоль оси x. Следствием применения параксиаль- ного приближения является утверждение, что векторы напряженности электрического и магнитного полей лежат в плоскости фронта волны, то есть электромагнитные волны поперечны. Однако, как показано в [1], данное приближение верно только для пучков с «крупной», в сравнении с 2, пространственной неоднородностью интенсивности. Для демонстрации этого утверждения запишем уравнения Максвелла для системы, в которой волна, среда и все оптические элементы однородны и бесконечны вдоль оси z. В этом случае все производные по z равны 0 и для волны, распространяющейся вдоль оси x, система имеет вид:

^ E y =- X М.,                         (1)

д t     ЕЕ0 дx дHz _   1 (д Ey дEx

^^^^^^^^^^^^^^^^^^^^^^^^^^в               ^^^^^^^в ^^^^^^^^^^^^^^^^^^^^^^^^^в         ^^^^^^^^^^^^^^^^^^^^^^^^в  ^^^^^^^в  ^^^^^^^^^^^^^^^^^^^^^^^в д t     ЦЦ0 ( дx   ду

Свиридова И.В., Дрязгов М.А., Коренченко А.Е., Бибикова Э.А.

Численное исследование продольной компоненты электрического поля в электромагнитной волне

∂ E_{x =} 1 ∂ H_z ∂ t εε ₀ ∂ y

Из (3) следует, что продольная компонента E_x равна нулю лишь для бесконечной плоской волны с однородным профилем интенсивности. Если распределение интенсивности в поперечном сечении пучка не является однородным, т. е. ∂ H_z ∂ y ≠ 0 , то такая ЭМВ содержит продольную компоненту, причем тем большую, чем больше ∂ H_z ∂ y . Таким образом, чем сильнее поперечная неоднородность электромагнитного поля, тем больше продольная компонента, и, значит, рассмотрение субволновых масштабов в оптике выходит за рамки параксиального приближения.

Как показано в работе [2], продольная компонента может влиять на остроту фокусировки пучка, которая имеет значение во многих областях: фотолитография, оптические диски памяти, конфокальная микроскопия, оптическая манипуляция, высокоразрешающая метрология, ускорение электронов. Диаметр фокального пятна при острой фокусировке света зависит от вида поляризации и от фокусирующего оптического элемента. Для гауссова пучка световое пятно получается уширенным из-за вклада продольной компоненты [3]. Однако в случае пучка с Бесселевым распределением преобладание продольной компоненты в фокальной плоскости способствует сужению пучка и вытягиванию фокуса вдоль направления распространения [4].

В настоящее время все больший интерес представляет исследование объектов субволновых масштабов и дополнительных степеней свободы пространственно-неоднородных оптических полей. Свет обладает собственными степенями свободы, которые связаны с осциллирующими во времени электрическим и магнитным полями. В квантовом рассмотрении правая и левая круговые поляризации электрического и магнитного поля соответствуют двум спиновым состояниям фотонов. Спиновые и орбитальные свойства световых пучков связаны друг с другом. Эту связь принято называть спин-орбитальным взаимодействием или оптическим спиновым эффектом Холла.

Поляризация света влияет на траекторию его распространения и, наоборот, траектория оказывает влияние на поляризацию [5]. Так, при смене знака циркулярности поляризованного по кругу асимметрично сходящегося пучка происходит сдвиг «центра тяжести» продольной компоненты ЭМВ в направлении, перпендикулярном оси распространения света. Величина сдвига мала и составляет значение порядка радиуса перетяжки пучка. Этот эффект был изучен теоретически и экспериментально [6, 7], однако его численный анализ, насколько нам известно, не проводился.

Цель работы состоит в разработке программного пакета для анализа продольной компоненты электрического поля при взаимодействии ЭМВ с различными оптическими элементами и численном исследовании явления поперечного сдвига «центра тяжести» продольной компоненты при прохождении лево- или право-поляризованной ЭМВ через половину линзы.

Математическая модель

Пусть световой пучок распространяется в немагнитной среде, не содержащей зарядов и токов. Система уравнений Максвелла в этом случае записывается в виде:

∂ H x = ∂ t	- 1 μ 0	' d E , . d У	d E y) - d z J ,	(4)	∂ E x ∂ t	= 1 εε 0	' dH. . d У	?.H 1 d z J ,	(7)
∂ H	- 1	(BE	BE A	(5)	∂ E	= 1	(BH	BH A	(8)
y =		x	z -		y		x	- z
∂ t	μ 0	v d z	d x J ’		∂ t	εε 0	v dz	d x J ’
BH	- 1	f d E,	BE )	(6)	BE	= 1	f dH	BH 1	(9)
z =			x -		z			x .
∂ t	^ 0	V d x	d У J ,		∂ t	^^ 0	V d x	d У J

Для численного решения системы (4)–(9) использовался метод конечных разностей во временной области (FDTD-подход) [8]. Вычислительный объем представлял собой прямоугольный параллелепипед с размерами 40λ × 40λ × 100λ. На границах помещалась специальная поглощающая среда (далее PML), оптические параметры которой были подобраны таким образом, чтобы предотвратить отражение света обратно в объем и обеспечить полное поглощение преломленного пучка внутри PML [9]. Расчеты проводились для различных пространственных разбиений и временных шагов, и было получено независящее от параметров сетки решение. Параметры моде-

Физика

лирования: длина волны излучения λ = 0,5 мкм, толщина поглощающего слоя PML ~ λ . Алгоритм был протестирован с помощью задачи об отражении/преломлении света на границе вакуум-диэлектрик. Вычисления проводились на суперкомпьютере Торнадо (ЮУрГУ).

Проверка выполнения формул Френеля

Для проверки достоверности результатов расчетов было смоделировано падение электромагнитной волны на плоскую границу прозрачной диэлектрической среды. Коэффициенты отражения и преломления в этом случае могут быть вычислены аналитически с помощью формул Фре-

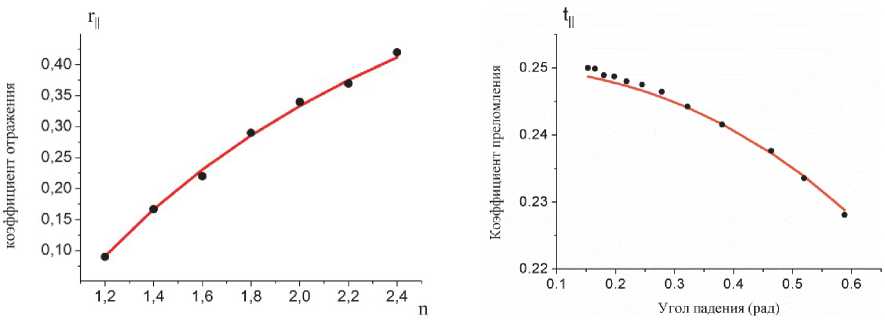
Рис. 1а. Зависимость коэффициента отражения света от показателя преломления среды при нормальном падении

• – расчет в программе FDTD-методом;

Рис. 1б. Зависимость коэффициента преломления света от угла падения; n = 1,5

–– – расчет по формулам Френеля неля. На рис. 1, а и б показаны результаты тестовых расчетов. На рис. 1, а изображена зависимость коэффициента отражения ЭМВ от показателя преломления среды при нормальном падении, на рис. 1, б показана зависимость коэффициента преломления света от угла падения при фиксированном показателе преломления (n = 1,5). Как видно из рисунков, результаты численного эксперимента хорошо согласуются с теоретическими значениями, погрешность составила менее 3 %, что говорит о высокой точности применяемого метода.

Исследование продольной составляющей электрического поля для плоско- и циркулярно-поляризованных электромагнитных волн, распространяющихся в вакууме

На рис. 2 показана интенсивность поперечной Еy (левая шкала) и продольной Ех (правая шкала) компонент электрического поля при распространении в вакууме линейно-поляризованного гауссового светового пучка. По оси абсцисс графика отложено расстояние от центра пучка вдоль оси y, выраженное в длинах волн, по оси ординат отложена интенсивность в условных единицах. Полуширина пучка по 1/е – спаду интенсивности (FWHM) на входе в вычислительный объем составляла 5λ. Как видно из рисунка, интенсивность поперечной компоненты в ~ 1000 раз превышает интенсивность продольной, это позволяет пренебрегать вкладом Ех в параксиальном приближении при описании, например, мод лазера. Интенсивность продольной компоненты излучения имеет вид двугорбой кривой, максимумы которой соответствуют наибольшим значениям

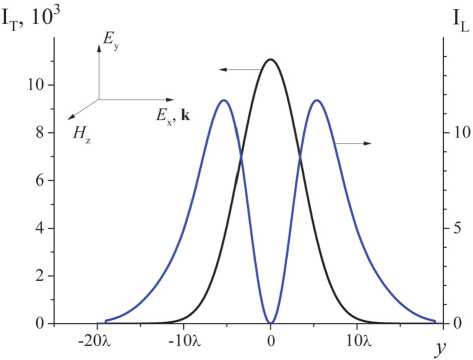
Рис. 2. Интенсивность в условных единицах поперечной (шкала слева) и продольной компоненты (шкала справа) при распространении линейно-поляризованного излучения Гауссова профиля в изотропной однородной среде

∂ H_z ∂ y .

При распространении такой же волны, но с циркулярной поляризацией, в пространстве наблюдалась динамическая картина изменения

Свиридова И.В., Дрязгов М.А., Численное исследование продольной компоненты Коренченко А.Е., Бибикова Э.А. электрического поля в электромагнитной волне продольной компоненты, показанная на рис. 3. Каждая картинка на рисунке представляет собой мгновенное распределение модуля Е х в поперечном сечении пучка. Зачерненные участки картинок соответствуют наибольшим значениям продольного поля (по модулю). Как видно из рисунка, картина продольного поля поворачивается со временем, это связано с вращением вектора магнитного поля. Распределение интенсивности продольной компоненты было рассчитано из этих данных усреднением по времени и качественно совпало с данными работы [10].

Рис. 3. Временная эволюция мгновенных распределений модуля продольной компоненты электрического поля для циркулярно-поляризованного гауссового пучка

Исследование продольной составляющей при прохождении плоско-поляризованной электромагнитной волны через линзу

Для исследования возможностей пакета в вычислительный объем была помещена плосковыпуклая линза. Материал линзы имел показатель преломления n = 2, радиус сферической поверхности составлял ~50 X , толщина линзы в самом широком месте ~5 X , рассчитанное фокусное расстояние было равно 10 мкм, что составляло 20 X . Линейно поляризованная плоская ЭМВ с гауссовым профилем интенсивности падала нормально на плоскую поверхность линзы. Радиус сгенерированного падающего пучка, определенный, как полуширина пучка по критерию 1/ е , был равен 5 X .

На рис. 4 показан график зависимости радиуса пучка от расстояния до линзы. Как видно из графика, линза формирует протяженный

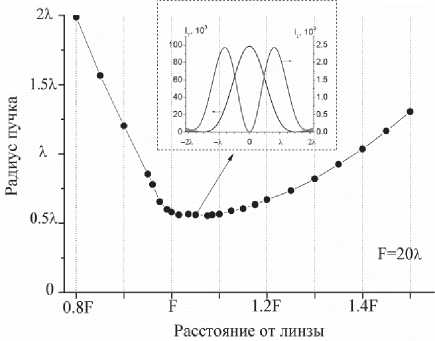
Рис. 4. Фокусировка светового пучка. Зависимость радиуса пучка от расстояния от линзы

(~ 2X) фокус c субволновым поперечным размером ~ 0,5X. Значение продольной компоненты зависит от степени неоднородности распределения интенсивности светового пучка, поэтому в фокальной плоскости линзы, в зоне, где пучок имеет наименьший радиус, продольная компонента должна возрастать. Как и ожидалось, соотношение интенсивностей продольной и поперечной компонент электрического поля в перетяжке составило ~ 40 (см. вкладку рис. 4), тогда как в падающем пучке это отношение составляло 1000 (рис. 1).

Изучение продольной компоненты электромагнитной волны на границе диэлектрик-вакуум

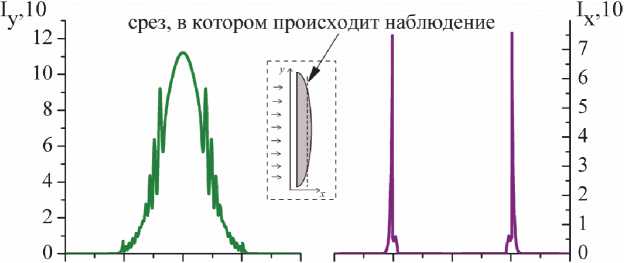
При изучении прохождения электромагнитной волны через линзу был замечен скачок продольной компоненты на границе диэлектрик-вакуум (со стороны сферической поверхности линзы). Схема эксперимента представлена на вкладке рис. 5. В плоскости, показанной на схеме, проводился расчет компонент электрического поля и усреднение квадратов их значений. Скачок возникает при переходе из материала линзы в воздух и связан с локальной поперечной неоднородностью диэлектрической проницаемости при выходе из линзы. Из рис. 5 видно, что как поперечная, так и продольная компоненты электрического поля реагируют на неоднородность среды резким локализованным скачком. Интерес представляет также интерференционная картина, возникающая внутри линзы. Колебания интенсивности в интерференционной картине показаны на

Физика

рис. 5 слева и возникают при сложении падающей и отраженной от внутренней поверхности линзы волн.

3                                                                                       2

• -ЮХ О ЮХ у -ЮХ О ЮХ у

• Рис. 5. Поперечное распределение интенсивности компонент электрического поля. Интерференционная картина внутри линзы (слева) и локальный скачок интенсивности на границе диэлектрик-вакуум (справа) Исследование сдвига «центра тяжести» продольной компоненты электромагнитной волны

В рамках создания универсального пакета для исследования взаимодействия ЭМВ с различными оптическими элементами была создана численная модель эксперимента, описанного в работе [7]. Геометрический спиновый эффект Холла – оптическое явление, демонстрирующее спин-орбитальное взаимодействие в световом пучке и заключающееся во влиянии состояния поляризации света на траекторию пучка. Для создания светового пучка в вычислительный объем помещалась половина линзы. Полученный асимметричный пучок обладал ненулевым орбитальным моментом. Спин-орбитальное взаимодействие приводило к тому, что траектории пучка для право- и лево-поляризованного света отличались друг от друга, что становилось особенно заметно в фокальной плоскости линзы. Анализ результатов численного эксперимента показал, что радиус перетяжки составил величину, примерно равную длине волны ~ λ , а в зоне фокуса было замечено смещение центра тяжести продольной компоненты пучка от первоначального направления на ~ 0,45 λ влево для левоциркулярно поляризованного пучка и на ~ 0,47 λ для правоциркулярно поляризованного пучка. На рис. 6 заметно смещение центра тяжести продольной компоненты пучка от первоначального положения, отмеченного вертикальной прямой, в плоскости, перпендикулярной распространению волны. Этот результат хорошо соотносится с экспериментальными результатами [7], что говорит о точности созданной программы и о том, что геометрический спиновый эффект Холла возможно получить численно решением уравнений классической электродинамики.

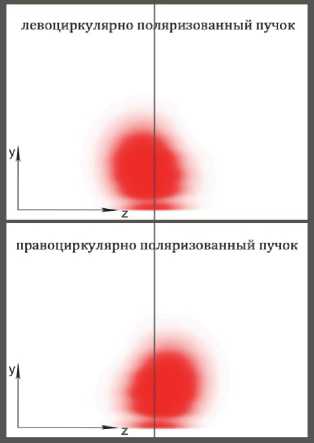
Рис. 6. Интенсивность продольной компоненты излучения в фокальной плоскости для пучков с различными спиновыми состояниями. Видно отклонение пучков от направления первоначального распространения, связанное со спиновым эффектом Холла

Заключение

Таким образом, в работе описан пакет программ для численного решения уравнений Максвелла, разработанный на основе метода FDTD. Пакет позволяет моделировать взаимодействие ЭМ излучения в оптическом диапазоне с различными оптическими элементами. Проведено тести рование пакета на основе сравнения коэффициентов отражения и преломления при падении ЭМВ на диэлектрическую среду с результатами применения формул Френеля. Получено хорошее согласие численных и аналитических данных, погрешность не превышала 3 %. С использованием разработанного пакета проведено численное исследование продольной компоненты электрического поля и получены следующие результаты:

• 1.    Анализ фокусировки светового пучка с помощью простой оптической линзы показал возрастание амплитуды продольной компоненты электрического поля в ЭМВ в ~ 25 раз в области

• 2.    Впервые численно изучен геометрический спиновый эффект Холла. Наблюдалось отклонение центра тяжести продольной компоненты асимметричного пучка от первоначального направления для пучков с право и лево-циркулярной поляризацией. Рассчитанный сдвиг пучка в фокальной плоскости половины линзы, создающей асимметричный пучок, составил ~ λ /2 при радиусе фокальной перетяжки примерно равном λ , что хорошо согласуется с литературными данными [6, 7].

Свиридова И.В., Дрязгов М.А.,                 Численное исследование продольной компоненты

Коренченко А.Е., Бибикова Э.А.                электрического поля в электромагнитной волне перетяжки. На границе диэлектрик-вакуум было замечено локальное возрастание продольной компоненты до величин, сопоставимых с поперечной компонентой. Эффекты связаны с возрастанием степени неоднородности поперечного распределения интенсивности светового пучка.

Работа выполнена в рамках темы государственного задания № 0389-2014-0030.