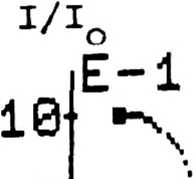Численное исследование пространственной структуры когерентных волновых полей оптического диапазона

Программы и алгоритмы решения прямой задачи теории волн, т.е. вычисление распределения волнового поля (ВП) в некоторой области пространства по заданному распределению поля и/или его производных на границе этой области можно рассматривать в качестве составного элемента систем автоматизации проектирования элементов плоской оптики (ЭПО) [1, 2].

В настоящее время в решении обратной задачи фокусировки волн в заданную область пространства с требуемым распределением интенсивности можно выделить три метода [3, 4]. Первый метод, широко используемый и наиболее развитый в математическом отношении, основан на приближении геометрической оптики [3, 5, б] . Вторая группа методов, учитывающая дифракционные эффекты, сводится к задаче минимизации соответствующих функционалов невязки, обычно решаемой итерационными алгоритмами [3, 4]. Третий метод решения задачи синтеза фокусаторов сводится к решению нелинейного [7] или линейного интегрального уравнения, связывающего распределение фазы или самого поля на фокусаторе с требуемым распределением интенсивности в фокальной плоскости.

Решение прямой дифракционной задачи является необходимым способом проверки и уточнения решений обратной некорректной задачи, особенно в тех областях применения указанных выше методов, где сложно или невозможно обосновать сходимость алгоритма, единственность решения (если это необходимо) или само существование решения в некотором классе функций. Этот факт, а также расширение областей применения и ужесточение требований к функциональным возможностям корректоров и фокусаторов когерентных волновых полей приводят к необходимости создания эффек- тивных программ детального исследования пространственной структуры формируемых этими элементами волновых полей с учетом дифракционных эффектов [1] .

В данной работе на базе известных вычислительных алгоритмов [8] созданы программы вычисления двумерного интеграла Кирхгофа для случая плоских формирующих элементов произвольной формы, проведено подробное тестирование этих программ с целью определения области их применимости, получена структура волнового поля в окрестности геометрооптической параболы, фокальной точки и осевого отрезка с равномерным распределением интенсивности. Изучено влияние изменения формы плоских оптических элементов и гауссовых неоднородностей интенсивности падающего пучка на пространственное распределение волновых полей.

1.    Математическая постановка задачи (интеграл Кирхгофа)

Опишем математическую постановку прямой задачи теории волн [9, Ю] , в paw-ках которой мы будем в дальнейшем работать. Пусть распространение монохроматической компоненты излучения в однородной изотропной среде описывается волновой функцией U (Р, t)»U (P)e^wt, удовлетворяющей временному волновому уравнению, причем комплексное волновое поле и(Р) удовлетворяет уравнению Гельмгольца

AU+k2U-0,                                  (1)

где к=2п/Л - волновое число, Р(х, у, z) - пространственная точка с координатами X, у, Z.

Пусть на плоский оптический элемент, расположенный в области (рис. 1) плоскости z=0, падает излучение в виде волны U(E, л, 0-0), которая преобразуется элементом в волну U(E, л, 0+0)=G(E, л) U(E, л, 0-0), где G(E, л) - комплексная функция пропускания плоского элемента. При этом преобразующий элемент является чисто фазовым, если |GI=1, чисто амплитудным, если ImG=0, а в общем случае можно рассматривать амплитудно-фазовые элементы с достаточно произвольной комплексной функцией G(Ez л) • Отметим, что здесь № не рассматриваем поляризационные эффекты. Тогда поле за элементом в полупространстве z^O описывается решением соответствующей краевой задачи для уравнения (1). Для первой краевой зада-

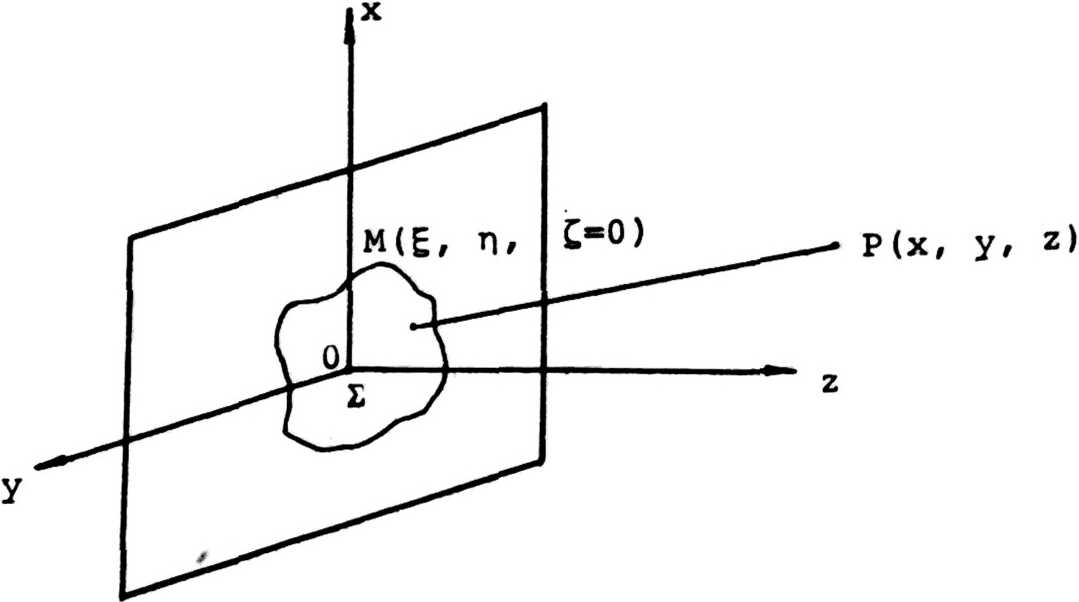
Рис. 1. Геометрия задачи чи (задано поле на границе области) решение уравнения (1) , используя метод функции Грина, можно представить в виде [9, 10] :

и(Р> = 5^7 У/ и(Е, п, 0+0) £ • 2— dEdn - ^ // Ф<Е« п)^ ‘ dEdn ♦ 2 ТЕЛ g                                                              J]

• ¹               ikr        .               _ „ikr

• + 577 JJ U(E, П, 0)| • 2-— dEdn-^T // ф(Е, n)p • S-p" dEdn, (2)

• ²ⁿⁱ S^E          Г r       zni _E         Г r

где S1 есть плоскость z»0, r3= (x~E)a + (уп) a+za, предполагается выполненным условие kr»l, ф(Е/ n)=U(Ez Пх 0+0) при М(Е, п)€Е.

Следует отметить, что в соотношениях (2) переход от интегрирования во всей плоскости S , к интегрированию по области Е требует определенной аккуратности в понимании граничных условий, особенно при постановке обратной задачи, когда по распределению поля в некоторой области находится поле на границе. Действительно, в реальном исполнении амплитудно-фазовый преобразователь имеет конечные размеры и может сопрягаться с непрозрачным экраном, или освещаться неограниченным пучком, или быть комбинацией этих случаев. Тогда в соотношениях (2) переход от области интегрирования S1 к I математически означает, что задано поле Ф (М) :ф (M)sU(M, 0+0) при М€Е и ф(М)=0 при MCS^E. Это приближенные граничные условия Кирхгофа первой краевой задачи. В случае сопряжения элемента с непрозрачным экраном это означает, что в (2) пренебрегают вкладом приграничного поля U(M6S1\E, 0+0), т.е. предполагается очень быстрое спадание поля U(M, 0+0) в области экрана. Для обратной задачи это означает, что в качестве ее решений допус каются поля U(M, 0+0) с инфинитным носителем, но с достаточно быстрым убыванием U(M, 0+0) вне фокусатора. В случае освещения элемента неограниченным пучком приближенные граничные условия Кирхгофа позволяют получить решение первой крае- вой задачи только с точностью до вклада от поля U(M€S1\E, 0+0).

Известны два широко используемых приближения интеграла Кирхгофа [9]. В приближении Френеля ikz и|р| - 1хГ

exp(in \z^Y~ ) //Ф(Е, n) exp (in ^^D-).

ехр[-12п(f E+f n)]dEdn где fx=x/(Az) f y/(Az). Область дифракции Френеля соответствует значениям волнового параметра D=Az/naa~l, где а - радиус или характерный размер апертуры, и значениям I ж—ЕI «1 ж ly-n I «1, r*z+l/2[ (х-Е)а+ (уп)а] •

Для области дифракции Фраунгофера D»l, exp[in (Е^П3)/ (Az)] «1 и поле описывается выражением ikz           а а

U(P) ⁼ 1X7" ^exP<ⁱⁿ ^l/ * ^Иф^- n)exp[-12n(f_xE+f n)]dEdn

Решения (3) и (4) обладают очевидной взаимностью, определяемой соответствием апертурных функций ф—*ф=фехр[1п (Еа+па)/ (Az).

В настоящей работе были программно реализованы на языке Фортран расчетные схеш Гаусса, Симпсона и формула трапеций для вычисления интеграла Кирхгофа. Сопоставление результатов предварительных расчетов, а также выво ды работы [11] определили наш выбор метода вычисления интеграла Кирхгофа (2) для произвольной плоской области Е (все дальнейшие результаты, если не оговорено специально, получены по методу Симпсона [8] на ЭВМ типа VAX. Следует отметить, что даже в задачах с осевой симметрией мы не использовали для вычислений соответствующих упрощений (например, суммирование по кольцам) и всюду пользовались единой расчетной схемой, пригодной для произвольной плоской области Е.

2,    Примеры вычисления интеграла Кирхгофа 2.1.    ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА КРУГЛОМ и ЭЛЛИПТИЧЕСКИХ ОТВЕРСТИЯХ

В приближении Фраунгофера дифракция плоской однородной волны

U*Ae^kZ (A=const, IM А=0) на круглом отверстии радиуса а описывается формулой (4) при ф(Е, п)=А. Интеграл легко вычисляется аналитически, и распределение интенсивности дифрагировавшей волны в плоскости наблюдения z=z0 дается известным выражением [9, 12]

2J (kaR/z)

I (R, z)=|U(R, z)|^a=I(0, z) ( y^_z---) ,                                  (5)

где 1(0, z)=(A/D)² - интенсивность на оси z, волновой параметр D»Xz/(па^а )»1, X - длина волны, R^a=x^a+y^a.

Численное интегрирование по формуле (2) при ф(Е, п)=А, а=10*²м,

Х=0.6328*10 6м,  z«5-103m, что соответствует значению волнового параметра Da10, согласуется с выражением (5) с точностью до 4-го десятичного знака уже на рас четной сетке 64 * 64 узлов, причем расчет значения поля в одной точке наблюдения занимает примерно 3,6 с.

В результате преобразования координат E’^U Er n,=U_,E в апертурной плоскости X       у z=0 (ux, u^ - вещественные постоянные) отверстие Е трансформируется в Е1 .

В приближении Фраунгофера из формулы (4) легко получить соотношение подобия для случаев дифракции плоской волны на отверстиях I и Е’ [12] . Математически это по добие для интенсивностей дифрагировавших волн записывается в виде

Кх, у, z) = (uxu )~а1' (х‘ , У1, z')

где х’®х/ц , y^y/u , т.е. при дифракции плоской волны на отверстии интенсив-х        у ность поля I1 в точке с координатами (х’, у1

X у X у ного из тестов программа вычисления интеграла интенсивности поля от дифрагировавшей плоской

z) имеет значение использовано нами в качестве од-(2) . Были вычислены распределения

волны на

эллиптических отверстиях

а с отношениями полуосей Ux/uy=l; 1.01; 1.5, причем для простоты

сравнения требовалось выполнение равенства и • U ”1, а X у

значения а, X, z сохра-

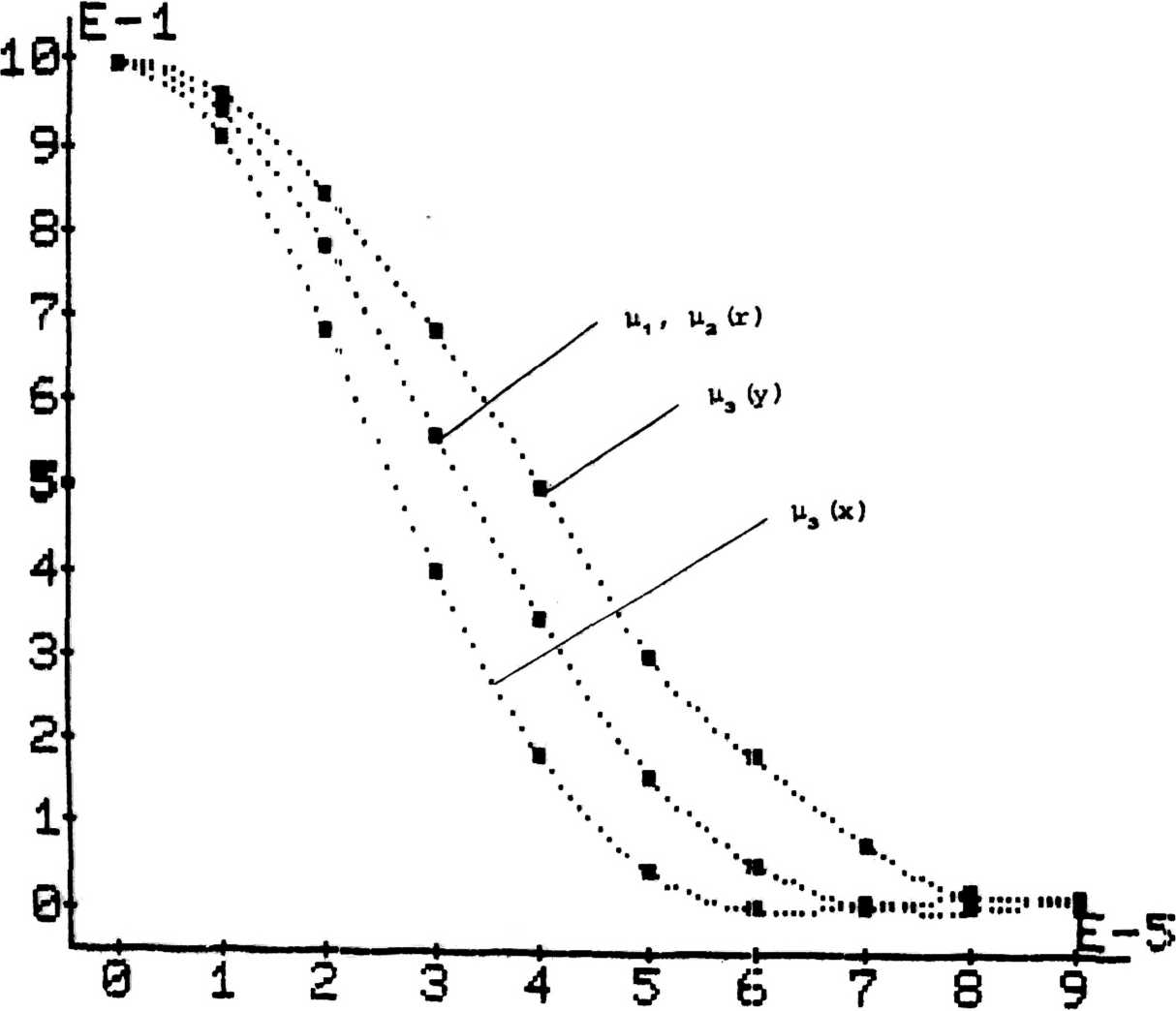
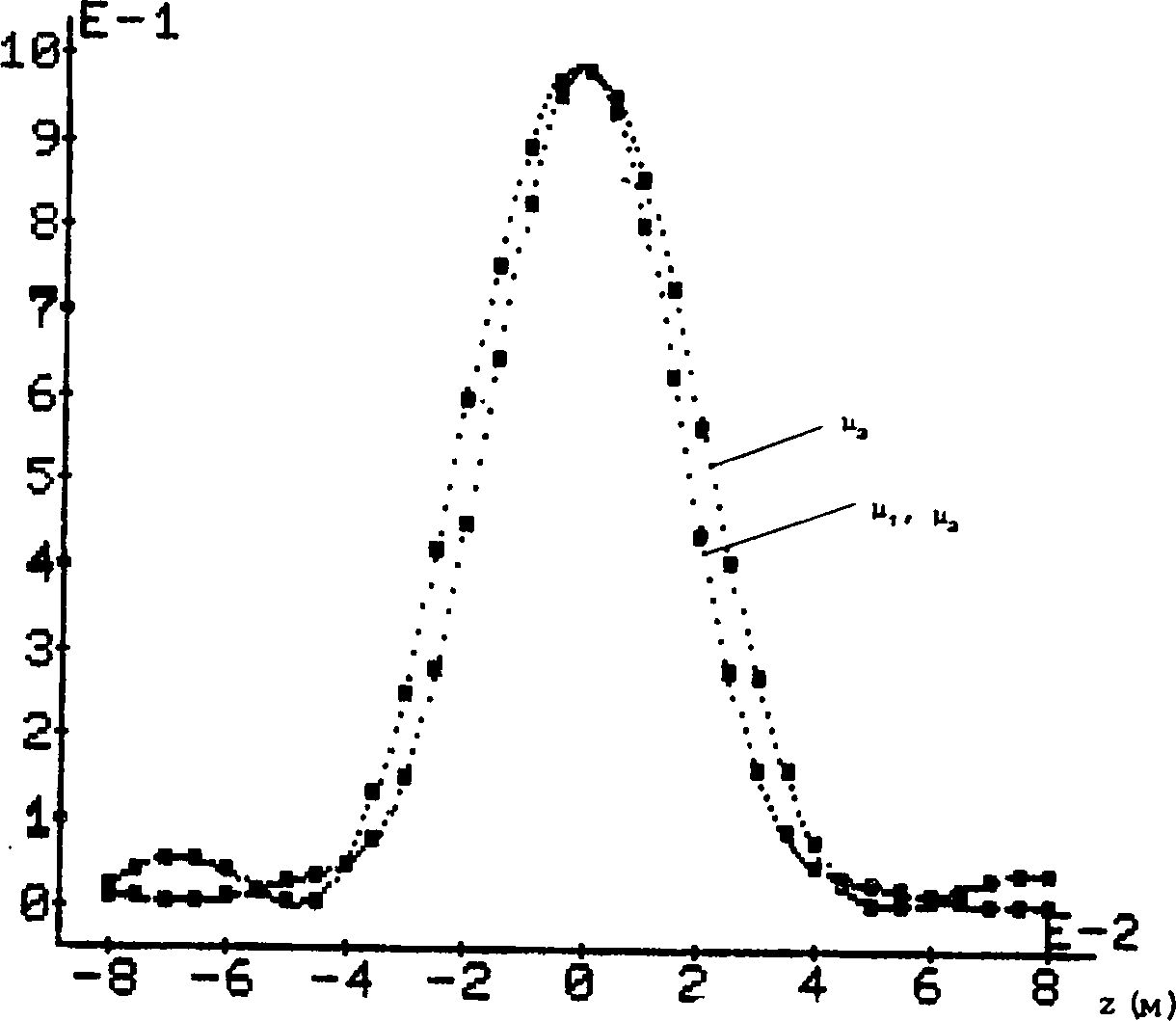
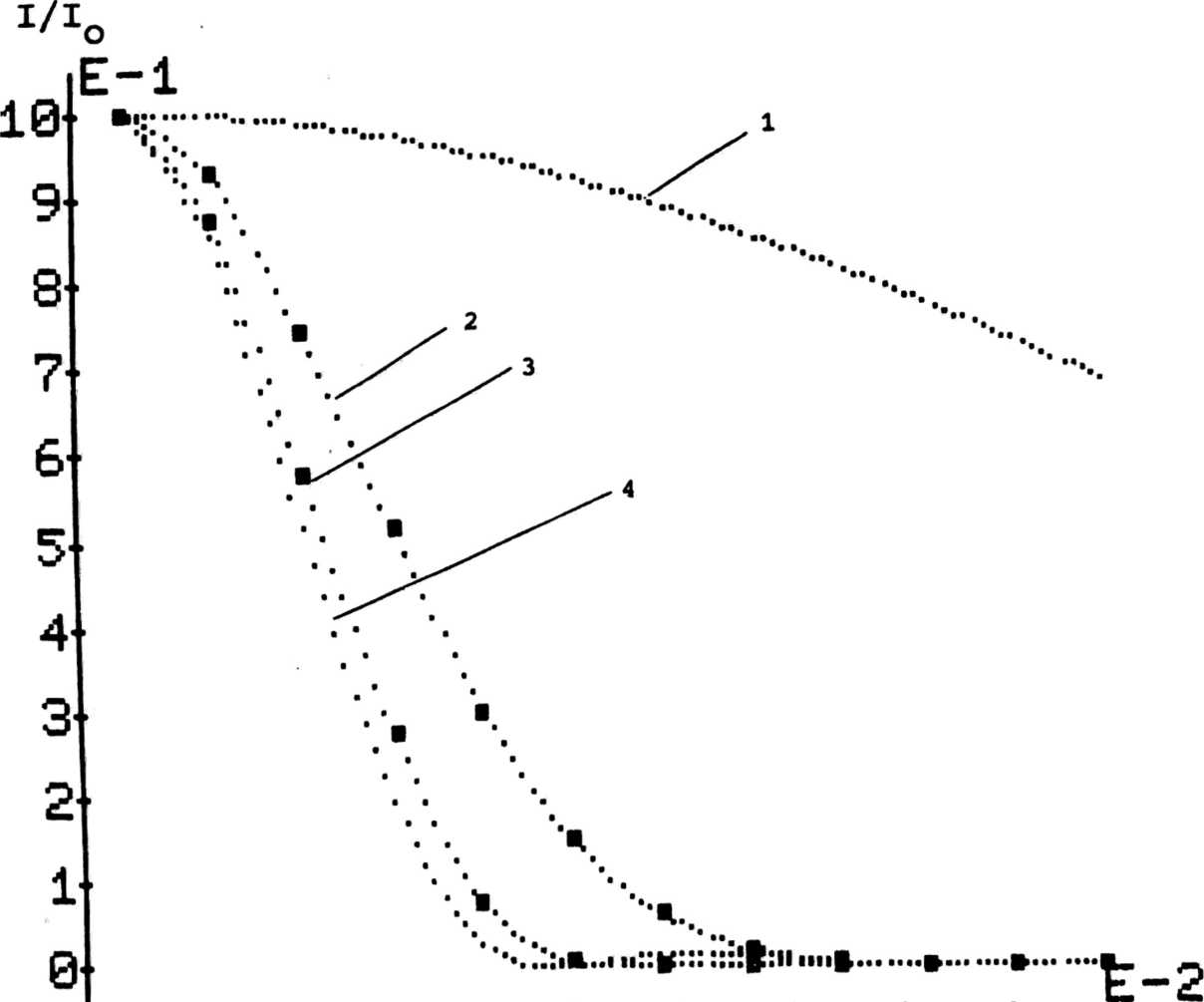
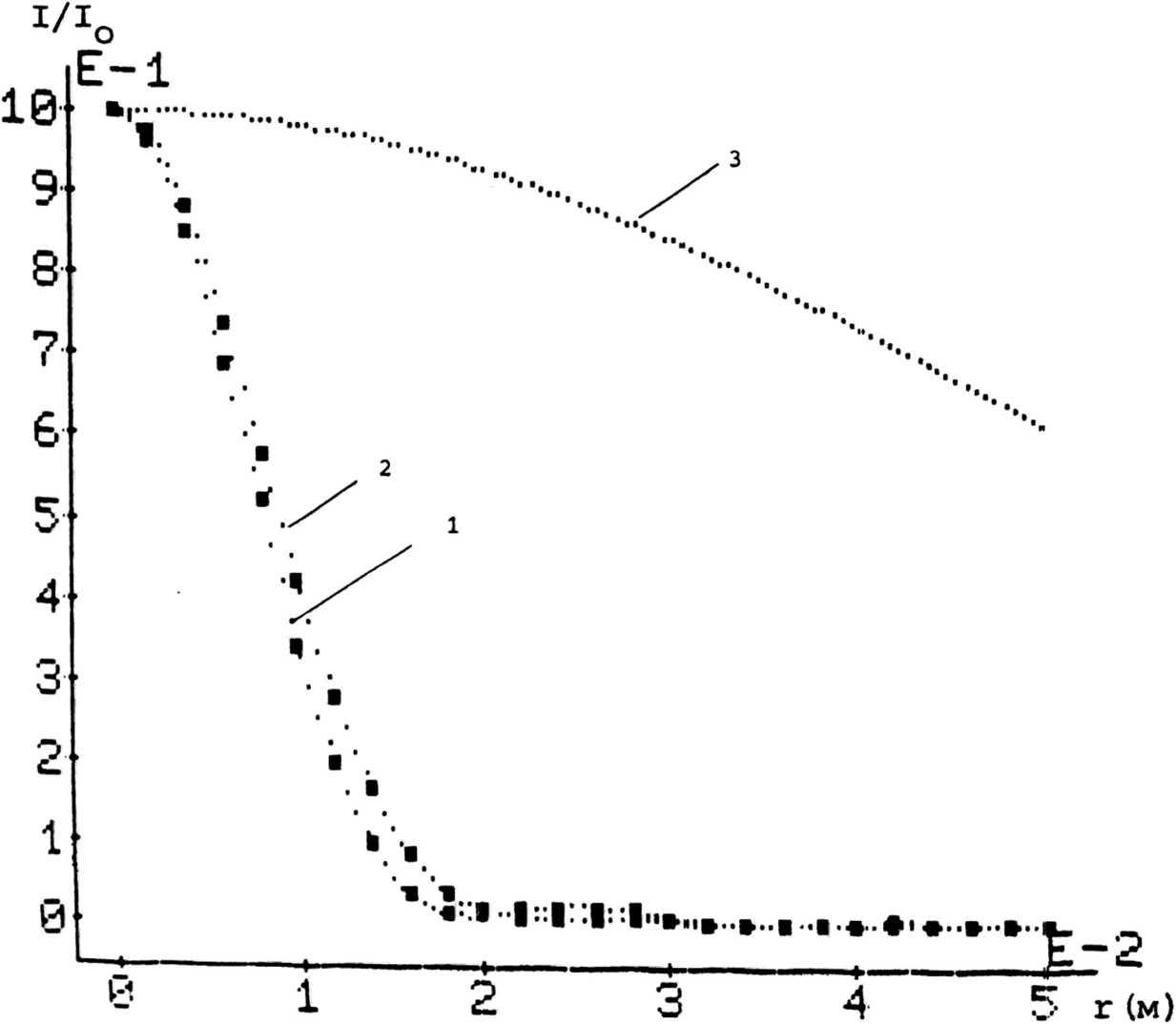
нялись такими же, как в случае дифракции на круглом отверстии расчетов в соответственных точках находятся в полном согласии

Е. Результаты с формулой (6),

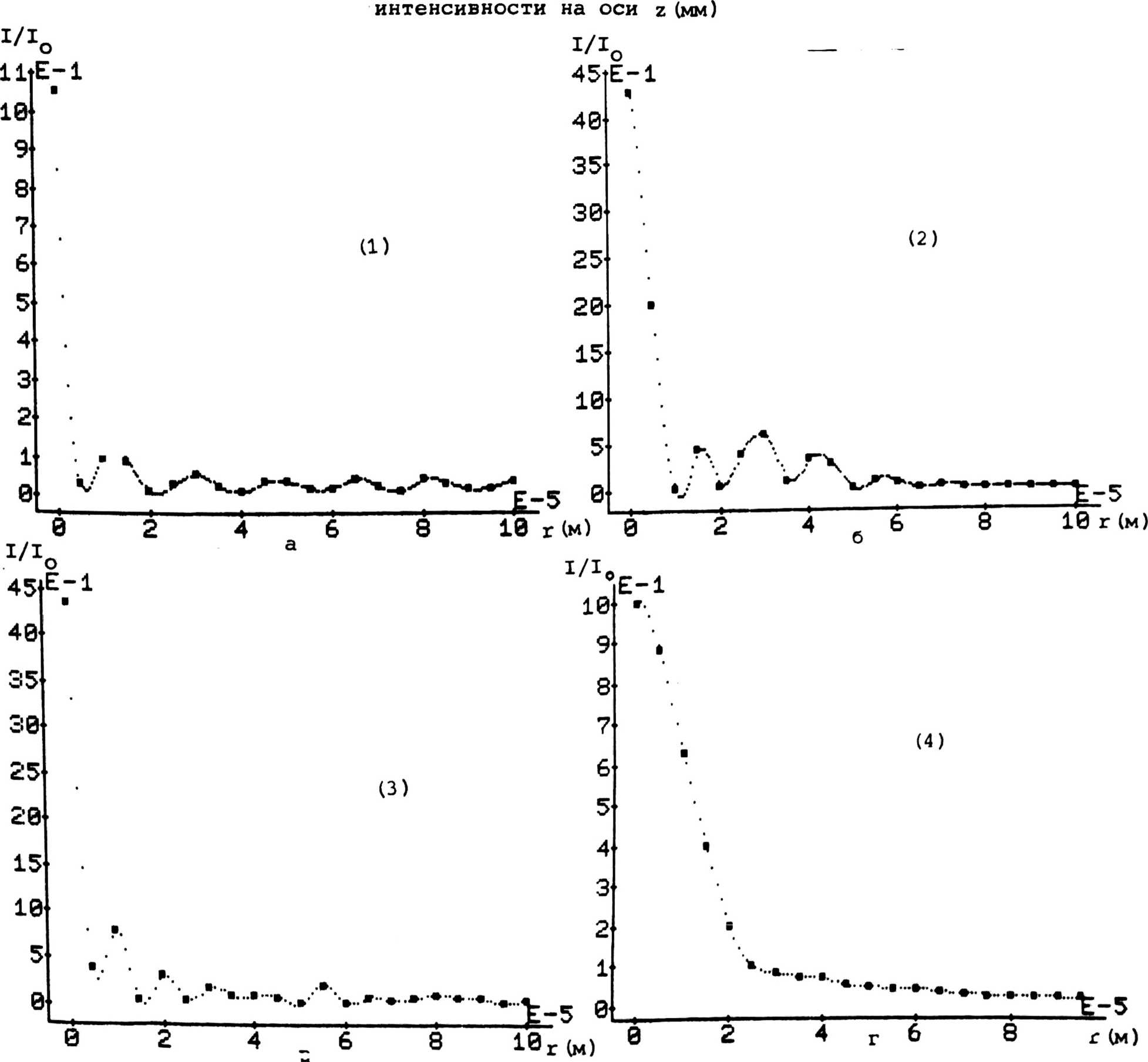
• 2.2.    СВЕТОВОЕ ПОЛЕ ВБЛИЗИ ФОКУСА

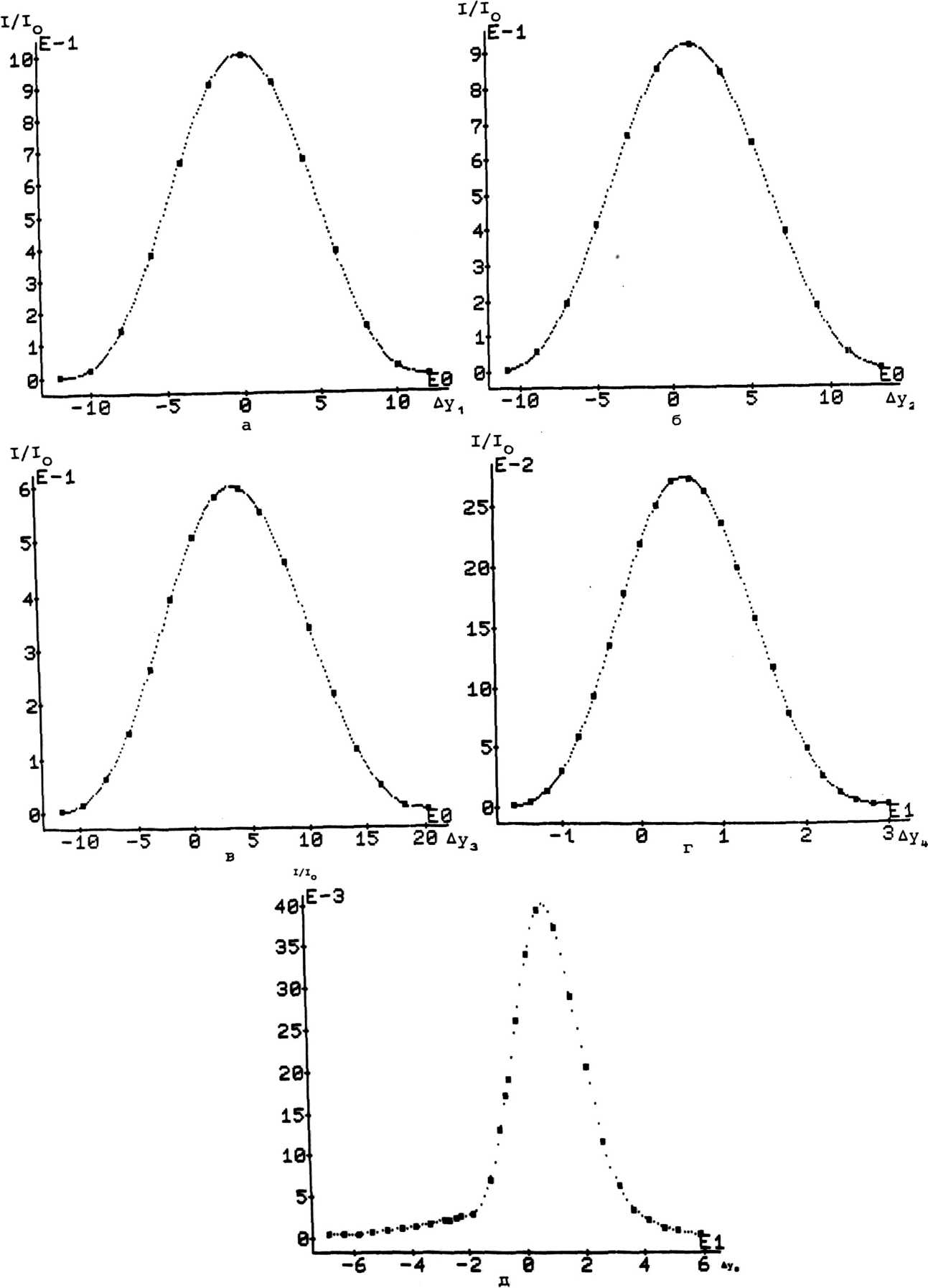
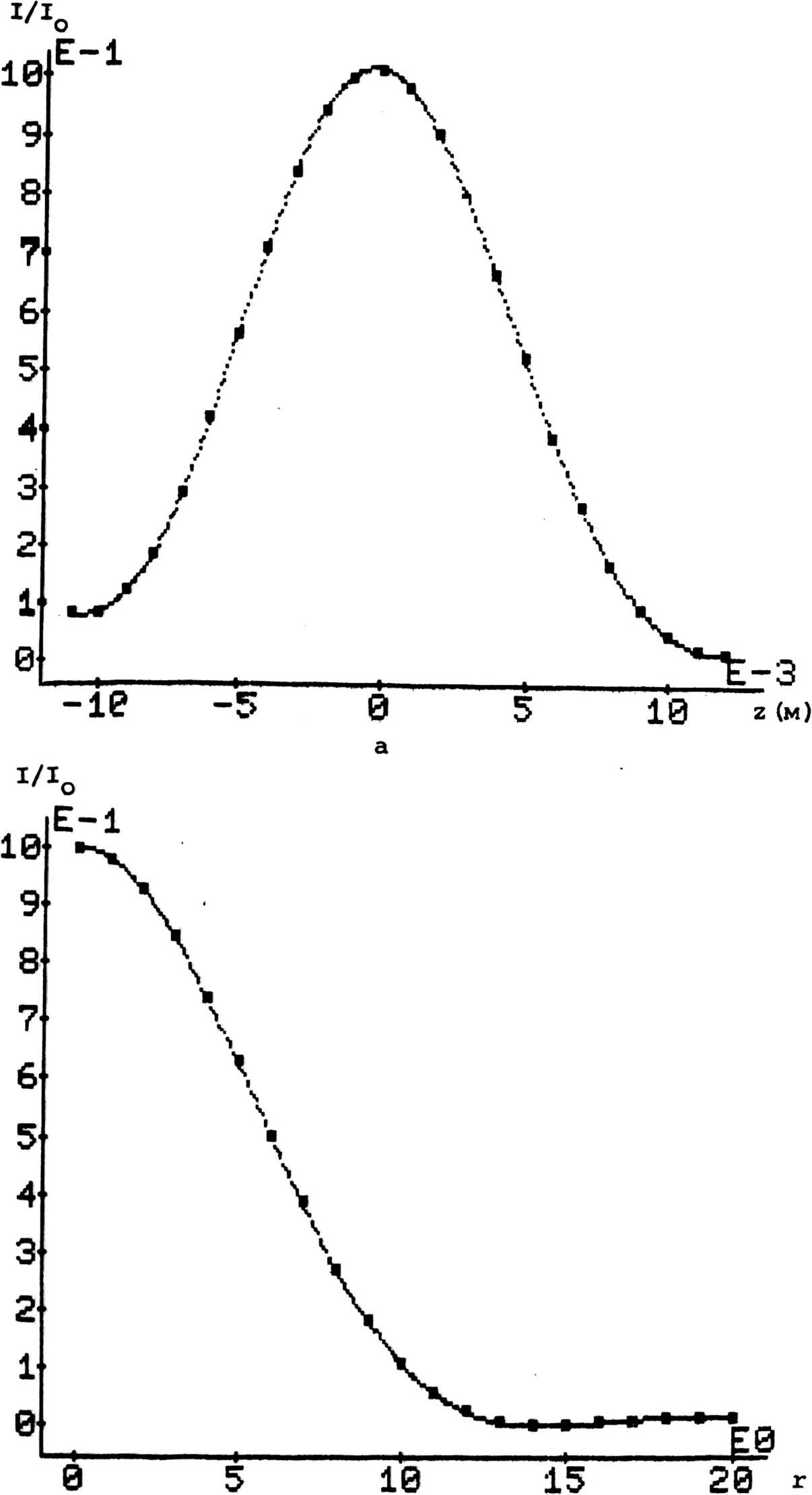
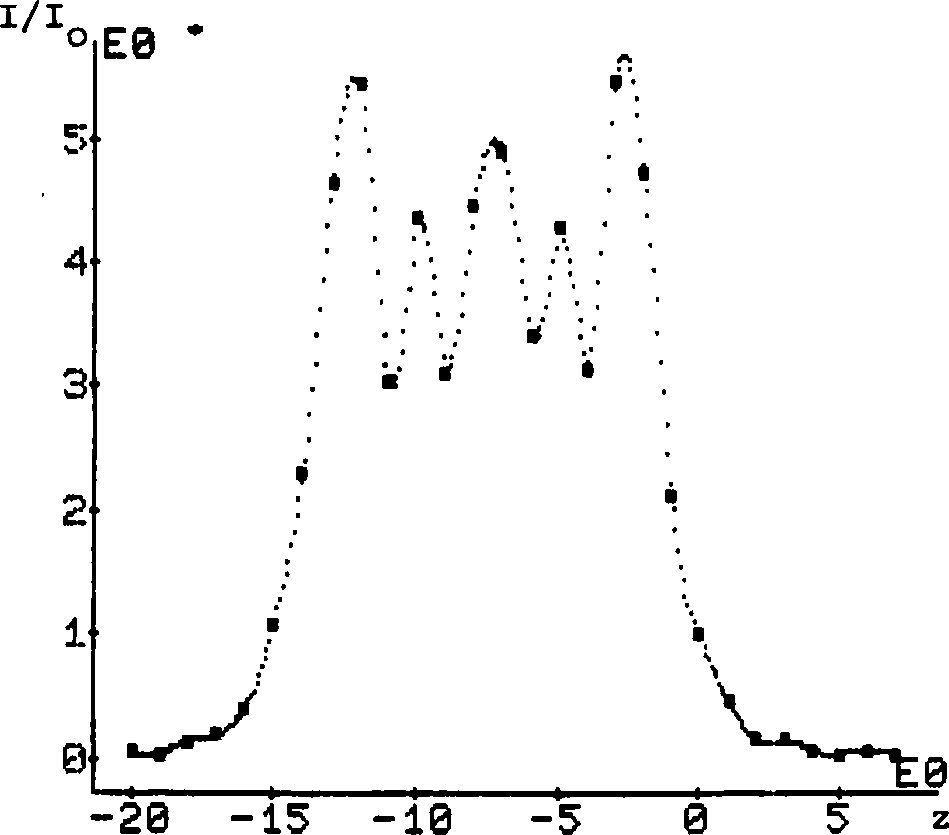
Исследуем численно дифракцию сферической сходящейся волны на круглом и эллиптических отверстиях. Сферическая волна, сходящаяся на оси z в точке Р(0, 0, zQ) , в плоскости апертуры описывается амплитудно-фазовым распределени ем

<р(Е, n)-Aexp(-ik/ га+Еа+па)/^ za+Ea+na“ (A/z0)exp[-ikz0 (l+(Ea+na)/2z£)], (7)

где z - фокусное расстояние линзы, А - вещественная постоянная и предполагает-ся, что для характерного линейного размера отверстия а справедливо соотношение a/zQ«l. При длине волны излучения Х=0.6328•10~ем и фокусном расстоянии z0*l м был проведен численный расчет интеграла Кирхгофа (2) с апертурной функцией Ф(Е, и) (7) для серии эллиптических отверстий {Е. 4 s Еа/и? ^П3/U2^*a?; l,j-l,2,3) при этом для каждого значения а^ из набора (at; а2; аэ)«(0.5; 11 1.5)-10 м отношения полуосей ц.=u ./и . принимали все значения из набора (ц., ц_ , U-) = J XJ yj

*(1; 1.01; 1.5). Для простоты сравнения результатов всегда требовалось выполне ние равенства 1^*и^=1, т.е. площади S^=4na? отверстий Б^ были независимы от U-. Некоторые результаты расчетов на сетке 128 * 128 узлов представлены на ри сунках и в таблицах к статье. Отметим, что время вычисления интеграла (2) в каждой точке наблюдения составляло *14 с.

На рис. 2 даны графики относительных распределений 1(х, у, z0> =

^jtx, У/ го)/1^(0, z=zo вдоль осей х и у

0, zQ) интенсивности светового поля в фокальной плоскости

(для круглого отверстия с 1^=1

распределение осесиммет

рично) .

В случае и1=1 (круглое отверстие) первый минимум In

При слабой эллиптичности отверстия с и2=1«01 максимальное отклонение распределений 11а(х, 0, z0) и 112(0, у, z0) от функции I1

(приведенные данные смотри также в табл. 1а, б) . Графики на рис. 2 обнаружива ют растяжение распределений интенсивности вдоль оси у и сжатие вдоль оси х в соответствии с тем, что апертурный круг сжимается по оси у и растягивается по оси х при деформации круглого отверстия в эллипсы. Этот факт, очевидно, согласуется с соотношением подобия (6), хотя последнее в данном случае строго не выполняется .

Рис. 2. Сферическая волна. Распределение интенсивности светового поля в фокальной плоскости: а =0.5*10^2м;

U1=l| Ua«1.01; Ц3*1.5

xijmin (м) yijmin	U1	Ua	U3
а1	8-10-= (127Л) 8-10“®(127Л)	7.5.10**= (118Л) 8.5.10“=(133Х)	6-10“=(95Л) 9-10“=(143Х)
а 2	3.8-10“=(60А) 3.8•10“®(60Х)	3.8 • 10**® (60Л) 3.8•10“=(60Х)	3.2•10_®(50Х) 4.8.10-=(75Х)
9з	1.9•10“®(ЗОХ) 1.9 • 10**® (ЗОЛ)	1.9•10”=(ЗОХ) 1.9•10~=(ЗОХ)	1.6.10-=(25Л) 2.4.10-=(38Л)

а

4j(xijmln' °' Zo> I±j(0, У^^т£П» zj	»1	и3	1*з
9i	8.10-“ 8-10**»	4•10-* 5.94.10-»	1.8.10-3 1.6-10-3
9 =	1.6.10-* 1.6-10-»	7.7.10-= 2.7•10”»	1.4.10—» 1.5-10“*
9з	1.68-10”» 1.68-10”»	7.9-10-= 2.8-10—»	1.4.10-» 1.5-10“»

б

Распределения относительной интенсивности 1^(0, 0, Дг)=1^(0, 0, Az)/

= 1^(0, 0, Azl/I^tO, 0, zQ) вдоль оси z вблизи фокуса zQ представлены на рис. 3, где Az=z-z0.

Обращает на себя внимание факт смещения максимальных значений

1^(0, 0, △^z₁j_max^ относительной интенсивности в сторону апертуры от фокальной плоскости z=z_Q (табл. 2). Величины и положения первых минимумов интенсивности перед фокальной плоскостью z=z_q и за ней для приведенных на рис. 3 графиков показаны в табл. За, б.

Приведенные выше данные свидетельствуют о заметной несимметрии относительно фокальной плоскости в распределении интенсивности светового поля вдоль оси z. Этот результат можно продемонстрировать аналитически в случае интеграла (4) с Ф(Е/ П) из формулы (7), хотя, например, в [12] встречается обратное утверждение.

Ввиду определенной качественной схожести результатов при указанных выше эна- чениях а^

мы не приводим графиков распределений интенсивности I3j (х, у , z) и

I3j (x, у, z) Uj (i f j = 1,

однако характерные параметры распределений для всех а^ и

2, 3) даны в табл. 1а, б, 2; За, б. В табл. 1а указаны положения xijmin и Уijmin первых минимумов в распределениях ^(х, 0, zq) и Iij ^' У' zq) интенсивности по осям х иу соответственно, значения этих миниму-

МОВ V^jmin' °' ^ и Ч?0' Xijmin

zQ) даны в табл. 16. В табл. 1а, б верх-

ние цифры в каждой клетке отвечают распределениям по оси х,

а нижние - по оси у

Дг±зтах (м)	Ui	и2	Уз
а1	-6110”** (952Х)	-8-10”** (1263Л)	-5.1-Ю”3 (8057Х)
аа	-5-10”=(8Х)	-6.10”=(95Х)	-3.10"=(47Х)
аз	-3.10”®(5Х)	-3-10”®(5Х)	-2.10-= (31/Х)

Таблица 3

Ч£п <м) 4jmin (М)	Ui	и.	и3
ai	-5.10”* 5.5.10”*	-5.10”* 5.5-10"*	-6.5.10”* 7.5-10”*
а2	-1.2'10”* 1.2-10”*	-1.3-10”2 1.3.10”*	-1.7.10”* 1.8.10”*
аз	-3.2.10”3 3.2-10”3	-3.2.10”3 3.2-10”3	-4.4.10-3 4.4-10”3

а

I. . (о, о, az)"?) . ) 13        ijmm I. . (0, 0, Az . ) ij '       ijmin	Ui	u3	u3
ai	1.5-10”3 7-10”**	1.58.IO”3 7.3-10”3	5-10-3 3.7-10”3
аз	4.4.10”3 1.8«IO”3	1.5.10”3 1.8-10”3	4.1-10-3 4.6•10”3
a3	5.6'10”= 2-10”**	5.6-10”= 2«10”**	4.3-10”3 4.3-10”3

б

В табл

I, . (О

За указаны положения ^z^j^n и ^ijmin пеРвых минимумов в распределении

О, Az) интенсивности вдоль оси z вблизи фокуса z=z

МУМО. ilj(0, 0. Д=М1п) „ ^.(0, 0, Az^

о, значения

этих мини-

даны в табл. 36, причем

в табл. За, б

верхние цифры в каждой клетке соответствуют положению за ним. в табл. 2 даны положения Az. . максимумов в

**                                           13 max

1чЯ0, 0, Az).

перед фокусом

распределениях

а нижние

Обратим внимание, что с увеличением а^ при данном

Uj происходит поджатие

фокального пятна как вдоль оси z, так и по осям х и у, при этом проявляется тенденция’ к восстановлению симметрии относительно фокальной плоскости z-z0.

VIO

Рис. 3. Сферическая волна. Распределение интенсивности светового поля на оси z:a1=O.5-lO”aM;

^=11 ца=1.01; цэ=1.5

• 2.3.    ПЛОСКАЯ НЕОДНОРОДНАЯ ВОЛНА С ГАУССОВЫМ РАСПРЕДЕЛЕНИЕМ АМПЛИТУДЫ

Встречающиеся на практике пучки излучения в результате случайных стационарных искажений поля или в силу своего происхождения (например, излучение одномодовых лазеров) часто оказываются неоднородными. Поэтому важно правильно оценивать и учитывать погрешности, вносимые различными неоднородностями поля падающей волны при фокусировке с помощью элементов, рассчитанных на случай плоских однородных волн. В данном разделе, в качестве модельной задачи, изучается влияние гауссовой амплитудной неоднородности на дифракцию плоской полны на круглом отверстии.

Для плоской волны с гауссовой амплитудной неоднородностью Ф(Е, п)=Аехр[-(Е2+и2)/Ь2] дифрагировавшее на круглом отверстии поле в приближении Френеля (3) описывается интегралом

I=/ipJ0 (vp)exp (- ~ p2)dp,                                                (8>

u(R, z) = -i2(A/D)elkzexp(i ^-) • I(u, v) , v»kaR/z»2R/Da, u=2 (a2/b2-iD 1), где a - радиус отверстия, b - вещественный параметр гауссова распределения, D»Az/na2 - волновой параметр, JQ - функция Бесселя нулевого порядка. Интегрирование по частям с использованием известных соотношений для функций Бесселя приводит к двум эквивалентным представлениям интеграла (8) в виде рядов по степеням отношений (v/u) или (u/v) с функциями Бесселя в качестве коэффициентов:

I(u, v)-v"1exp(- ^)Jo(H)nJn+i(v);                                    (9)

Ku, v)-u~1 {exp(- ^)-exp(- ^n$i(" u^^n^^ *                     ^°^

Выражения (9) и (10) полезны для аналитических оценок поля (8) в зависимости от поведения параметра неоднородности (а/Ь) и параметра D. Они являются рядами Неймана [13] и, как можно показать, имеют бесконечные радиусы сходимости - сходятся при любых значениях переменных и и v.

При заданных D и (а/Ь) из (9) или (10) легко получить значение поля (8)

на оси (R*0):

lim I(u, v)eu*1[l-exp(-u/2)].(11)

R*o

Согласно (8) интенсивность поля определяется выражением:

I(R, z)-lu(R, z) la-(A/D)a-4. |i(u, v)|a.(12)

В случае дифракции квазиоднородной волны интенсивность поля на оси получается на (11) и (12) в результате двойного предельного перехода lim limKu, v) a/b*o R-o

Iunif(0, ^-(A/D)3^^ ina(l/2D).(13)

В приближении Фраунгофера D»1 из (13) получается известное значение Wf^' =)-UVD)a.

. Из (11) легко оценить влияние неоднородности (а/b) на интенсивность поля на оси в приближении Фраунгофера:

1(0, z)lD>>1-(A/D)a(aa/ba)~a[l-exp(- аа/Ьа)]а=

J(A/D)a при а/Ь«1                                                      <14>

|(A/D)a(aa/ba)~a«(A/D)a при а/Ь»1.

Как следует из формулы (14) , для заданных параметров А и D наблюдается монотонное ослабление интенсивности поля на оси при увеличении неоднородности а/Ь, что, очевидно, связано с уменьшением интеграла энергии Лф(Е, n)l²d£dn падающего пучка.

При заметной неоднородности а/Ь»1 и некотором заданном значении параметра D, что соответствует большим значениям переменной и, и для не слишком больших значений v, разлагая в формуле (10) функции Бесселя по переменной, легко получить выражение для

Ku, v) «и*1 [1-ехр(- и/2)]ехр(- ^) .

Следовательно, как для приближения Френеля D“l, так и для случая D»1 при а/Ь»1 из (12) получаем экспоненциальное распределение интенсивности по R:

’»»»»»«<«- «'-Ф1 Й-а»р(- —^—' I .                  ИЯ

Daa (ая/Ьа)

которое при R«0 совпадает с (14).

В случае слабой неоднородности а/Ь£1 и не слишком малых D£1 из формулы (9), ограничиваясь первым членом ряда, получаем

Ku, v)-exp(-u/2)•v~1Ji(v) + 0(v"aJa(v)exp(-aa/ba)).                    (16)

Следует подчеркнуть, что остаточный член О( |u|v*"aJa (v) • exp(-aa/ba))~exp(-aa/ba)-2[(aa/ba) ^D"3]"1/3

будет достаточно малым даже при а/Ь«1, т.к« рост |и| при увеличении неоднородности а/b подавляется уменьшением ехр(-аа/Ьа) . Следовательно, функциональный вид (16) интеграла I(tt, v)*exp(-u/2)vw1Ji(v) будет справедлив не только при D»1 и а/Ь«1, но и при менее ограничительных условиях 0^1, а/b^l. Интенсивность поля в этом случае определяется выражением:

I(R, z)=(A/D)2exp(-2a2/b2)[2v*1Jn(v)]2.(17)

Приведем еще один способ получения выражений (15), (16) , (17) для приближения Фраунгофера D»l. В этом случае интеграл (8) при слабой неоднородности а/Ь«1 принимает вид:

I (u, v)=I(0, v)=/1pj (vp)dp=v^1 J (v) , о ° который соответствует формуле (17). Для случая D»1 и сильной неоднородности а/Ь»1 верхний предел интегрирования в (8) можно распространить до * и мы приходим к выражению

1= /1pJ (vp)exp(- — p2)dp^/pj (vp)exp(- — p2)dp= 0                  b2         0 °b l,a2x_1    , v2 x

« 5<—) exp(),

• ² b²        - 4(a²/b²)

• 2.4.    ВОЛНОВАЯ КАРТИНА ПОЛЯ ПРИ ГЕОМЕТРООПТИЧЕСКОЙ ФОКУСИРОВКЕ В ПАРАБОЛУ, В ТОЧКУ И ОСЕВОЙ ОТРЕЗОК

соответствующему формуле (15) .

Результаты численных расчетов интеграла Кирхгофа (2) для различных случаев дифракции плоской неоднородной волны ф(Е< п)=Аехр[-(Е^а+п²)/Ь²] на круглом отверстии радиуса а представлены на рисунках 4а, б и полностью согласуются с выводами предшествующего анализа. Действительно, как для случая 0=10 (рис. 4а), так и для 0=1 (рис. 46) кривые радиального распределения относительной интенсивности поля вплоть до неоднородностей (а/Ь)^1 хорошо описываются зависимостью I/I ~4v”²J²(v), отвечающей плоской однородной волне, причем положения ^v           1

первого минимума определяется нулем 3.832 -vm^n=2R/Da функции Бесселя J1 (v) . Рост неоднородности а/b^l падающего пучка приводит к монотонному переходу от зависимости (17) к выражению (15). Отметим, что в рассматриваемых случаях используемая программа расчета позволила устойчиво вычислять 2-3 боковых максимума (минимума) в распределении интенсивности.

Отметим, что результаты по анализу влияния гауссовой амплитудной неоднородности для частного случая D»1 дифракции плоской неоднородной волны на круглом отверстии представлены также в работе [1б], где получено разложение поля типа формулы (9), но в другой форме. Для указанного частного случая выводы работы [16] согласуются с выводами данного раздела.

Большие успехи в решении задач синтеза оптических элементов в значительной степени связаны с применением геометрической оптики [1, 3-6, 14, 15]. Однако учет эффектов дифракции делает необходимым описание работы оптических элементов волновой теорией. В данном разделе в рамках интеграла Кирхгофа (2) проводится численное исследование волновой картины полей, формируемых плоскими фазовыми элементами с апертурными функциями ф(Е/ и), полученными решением обратной задачи в приближении геометрической оптики.

По формулам работы [14] была рассчитана апертурная функция ф(Е, п) плоского оптического элемента, фокусирующего в геометрооптическом приближении плоскую волну в часть параболы y=x²/2R, xe[-d, d], расположенную в фокальной плоскости z=f, при этом значения параметров задачи были следующими: длина волны излучения А=1,06*10~⁵ м, радиус фазового элемента a=12.8«10^w3 м, фокусное расстояние f^B3-lO~¹ м, 2d=6*10"³ м, R=5»10“² м. Результаты вычисления интеграла (2) с ука-

0 3 10 15 20 25 30 35 40 45 г(м)

Рис. 4. Радиальные распределения относительной интенсивност] поля 1±(К, zl/I^O, z):a=10~2M, Л=0.6328*10"бм

• a)    0=10, {(а/Ь)₁}=(0.1_? 1, 2; 10} 1-1,2,3,4;

• б)    D=l, {(a/bip-tO.l; 1; 10}, 1=1,2,3

занной апертурной функцией <р(£, п) на расчетной сетке 512 х 512 узлов приведены на рисунках 5, 6. Все распределения интенсивностей нормированы на интенсивность I (0, 0, f)

В фокальной плоскости z=f распределения интенсивности по оси х, представленное на рис. 5, симметрично относительно х=0 .

Больший интерес представляет структура поля излучения в окрестности геомет рической параболы y=x2/2R. Численные расчеты поля в фокальной плоскости z=f представлены на рис. 6 в виде распределений относительной интенсивности вдоль оси у при значениях (х0, х1Г х2, хз, xQ)=(0; 1; 2; 2.5; 3) х Ю~3м. Максимумы этих графиков смещены от геометрических значений y^=x?/2R соответственно на значения: Дуо=0; Ду1*1.12•105 м (=Л);

Дуа = 7.54 • Ю^мС^А); Дуз~5.41•10~5m (=5А);

Ду^ = 7.96 • 10** 5м (а8А), где Ау^у-у^.

Волновая ширина параболы, определяемая расстоянием между первыми минимумами на распределениях рис. 6, изменяется от 2.54-10w4m (-24А) при xq=0 до 13.46 • Ю-^м (*127А) при х^=3 • Ю"3 м . Максимальные значения интенсивности на распределениях рис. 6 заметно падают к концам парабол и при выбранных выше значениях x^(i=0, lz 2, 3, 4) имеют значения: maxI(xQ, у)=1;

maxl(x , у)-0.921; maxi (х , y)^0.579;

maxl(x3, у)а0.274; maxi (х^, у)=0.04.

Следовательно, ближе к концам параболы происходит ослабление фокусировки излучения, выражаемое как в понижении максимальной интенсивности, так и в размытии области фокусировки. Вычисление интеграла энергии //1(х, у, f)dxdy по окрест-

9"

S'

?■■

6-5-4..

3"

Рис. 5. Фокусировка в параболу» Распределение относительной интенсивности поля на оси х(м)

Рис. 6. Фокусировка в параболу. Распределение относительной интенсивности поля вдоль оси ДУ. (Л)в плоскости z=f при значениях {хр = {0; 1; г^г.З; 3}мм ности отрезка параболы показывает, что он составляет 84% от энергии плоской волны, падающей на обсуждаемый фазовый элемент площади 4па2.

Расчеты интенсивности поля I (0, 0, Az) вдоль оси z вблизи z=f показывают, что глубина параболы (расстояние между первыми минимумами z — распределения интенсивности) составляет **3.6 • 10**2Mr а максимум интенсивности смещен на ~ -З’Ю^м («ЗОЛ) в сторону оптического элемента).

Следуя работе [14], предельным переходом R-*» и d-*0, преобразующим фокальную параболу в точку, была рассчитана фазовая функция ср (Ег п) плоского оптического элемента, фокусирующего в геометрическом приближении плоскую волну в фокальную точку. На основе этой фазовой функции, путем вычисления интеграла (2) на расчетной сетке 128 х 128 узлов была изучена структура поля в окрестности фокальной точки Р(0, 0, f) , при этом длина волны X, радиус элемента а и фокусное расстояние f оставались такими же, как в случае фокусировки в параболу.

Распределение поля по оси z на рис. 7а имеет максимум относительной интен сивности, смещенный в сторону фазового элемента на величину Д2тах=2тах"^= = -З-Ю'^м («ЗОЛ), а первые минимумы располагаются в точках Az~ = ll • 10”3 м и Az ^ «12 • 10~3m перед и за геометрооптическим фокусом, соответственно. Указанное z - распределение несимметрично как относительно фокальной плоскости z=f, так и относительно zmax< В радиальном распределении в фокальной плоскости (рис. 76) минимум интенсивности находится на окружности радиуса Rmin«14A.

В работе [15] дана функция пропускания фазового оптического элемента, фокусирующего в геометрооптическом приближении плоскую волну в осевой отрезок с равномерным распределением интенсивности. Функция описывается формулой:

ср(£, П )=с~1 ln[-2o/p2+f+cp2)2+2c2p2+l+2fc] ,                                (18)

где р2-Е2^П2; f - фокусное расстояние; с=к/а2; а - радиус фокусатора; длина отрезка и берется отрицательной, если область фокусировки располагается перед фокусом, и — положительный, в противном случае. Для значений Л—0.6328•10~6м, f=3.l0^1M, а=1.28-102м и х= -1.5-10~2мг таких же, как в [15] путем численного расчета интеграла (2) с апертурной функцией (18) нами была исследована волновая структура поля в окрестности осевого отрезка. Расчет производился на сетках 256 х 256 и 128 х 128 узлов. Последующие результаты приводятся для случая сетки 256 х 256 узлов, хотя данные для обеих сеток отличаются незначительно.

На рис. 8 дан график z - распределения относительной интенсивности 1(0, Az)=I(0, Az)/1(0, 0) по оптической оси, где 1(0, 0) интенсивность в фокальной точке и Дz=z-f. Отклонения в максимумах интенсивности относительно уровня „        о w равномерного распределения Iqp^*”1-^ 5^^' Д2)^2~3.66 доходят до 36%.

Радиальные паспоеделения относительной интенсивности I (R, Az) = =1 (R, Az)/I(0, 0) в перпендикулярных оси z плоскостях Az=(-15; -10; -5; 0) мм представлены графиками (1) , (2), (3) , (4) на рис. 9. Волновая ширина отрезка, определяемая по радиусу существенного затухания поля, имеет в соответствующих сечениях значения: R . =0.7^10~им; R . =1.9«10*4м; R «R , =1.4-10"цм.

iinin              2Ш1П              зш1п umin

Поток энергии Е ^z_k)=2n/^R°I (R, Az^)RdR, вычисленный в каждом из указанных сечений Az_k(k= 1, 2, 3, 4) в пределах от 0 до радиуса R_q=10“⁴m, имеет следующие значения, нормированные на поток энергии, падающей на фокусатор плоской волны: Е (A _Zl)=0.15, Е (A z_a)«0.41, Е (A z₃)=0.51, E(AzJ«0.2.

Полученные данные показывают, что оптический элемент с функцией пропускания (18) фокусирует плоскую волну в осевой отрезок, имеющий значительную неравно-

Рис. 7. Распределение интенсивности поля в окрестности фокальной точки: а) на оси г, 6) по радиусу И (А.)

мерность распределения поля как вдоль оси z, так и заметные отклонения вира определениях поля от сечения к сечению. И и z - распределения поля, представ ленные на рис. 8, 9, имея качественное сходство, количественно отличаются от данных работы [15], что, по-видимому, связано с использованной в [15] приближенной методикой вычисления интеграла Кирхгофа через разложения по функциям Ломмеля.

-60-

Рис. 8. Фокусировка в отрезок. Изменение относительной

Рис. 9. Фокусировка в отрезок. Радиальные распределения относительной интенсивности при (Az^}=— {15? 10; 5; 0} мм

Заключение

На базе метода Симпсона создана и подробно тестирована программа расчета двумерного интеграла Кирхгофа для широкого диапазона значений волнового параметра и произвольной формы плоских оптических элементов. В случае дифракции сферической сходящейся волны на круглом и эллиптических отверстиях - распределение поля несимметрично как относительно фокальной плоскости, так и относительно максимума в z - распределении. Эта несимметрия имеет тенденцию к уменьшению при увеличении площади апертуры. Аналитическое и численное исследование дифракции плоской неоднородной волны с гауссовой амплитудной неоднородностью на круглом отверстии показывает, что в диапазоне значений параметра неоднородности 0<а/Ь<1 влияние неоднородности незначительно. Можно ожидать, что этот вывод до определенной степени справедлив для случая эллиптических отверстий (в качестве а следует брать большую полуось) и смещенных центров отверстия и гауссова амплитудного распределения. Изучение волновой структуры поля в окрестностях геометрооптической параболы, точки и осевого отрезка наглядно показывает, что решение задач синтеза плоских оптических элементов во многих практически интересных случаях требует существенно волнового подхода или последовательного учета дифракционных эффектов при решении обратных задач оптики в приближении геометрической оптики.