Численное исследование решетчатого метаматериала в моделях со смешанным типом конечных элементов

РОССИЙСКИЙ ЖУРНАЛ БИОМЕХАНИКИ № 3, 2025RUSSIAN JOURNAL OF BIOMECHANICS

В настоящее время персонализированные эндопротезы, изготовленные аддитивным способом, активно используются в артропластике [1 –3] . Это связано с возможностью формировать неоднородную структуру эндопротеза в зависимости от эксплуатационных нагрузок и геометрических особенностей костного органа, подлежащего замене [4 –6] , что при правильном проектировании позволяет не только уменьшить вес, но и регулировать жесткостные, прочностные и структурные свойства изделия [7 –9] . В основном формирование структуры производится с помощью методов оптимизации или структурного проектирования [10; 11] . После формирования неоднородных изделий осуществляются проверочные расчеты напряженно-деформированного состояния методом конечных элементов (КЭ). Однако после производства таких изделий наблюдаются дефекты, влияющие на физико-механические свойства. К таким дефектам можно отнести: наличие макро- и мезопористости [12; 13] , остаточных напряжений [14; 15] и геометрической погрешности изделия при производстве [16; 17] и эксплуатации [18; 19] . Определение структурных и геометрических дефектов можно осуществить с помощью методов компьютерной томографии [20 –23] . Для учета указанных погрешностей при конечно-элементном анализе необходимо заранее провести дополнительные натурные испытания, чтобы определить влияние этих дефектов на физикомеханические свойства [24 –26] . Это, несомненно, представляет собой трудоемкую задачу, обладающую значительной временной и материальной сложностью. Но даже без учета данных дефектов наблюдается тренд на некорректное использование конечно-элементного анализа изделий, используемых в медицине [27 –29] .

Степень дискретизации и граничные условия конечно-элементной модели являются ключевыми компонентами численного анализа, влияющими на точность решения [30–32]. Степень дискретизации можно оценить с помощью исследования сеточной сходимости. Сеточная сходимость зависит от характера и порядка функций аппроксимации элементов, а также от характера конечно-элементной сетки. На характер сетки оказывают влияние как форма, так и размер конечных элементов. Так, у одномерных моделей с элементами, имеющими квадратичную аппроксимацию, сеточная сходимость достигается на менее густой сетке по сравнению с элементами, обладающими линейной аппроксимацией. Для моделей, использующих гексаэдральные элементы, наблюдается аналогичная тенденция в сравнении с тетраэдрическими элементами.

Тетраэдрические элементы чувствительны к форме конечного элемента, что приводит к ложным осцилляциям узловых значений, или, как это часто называют в литературе, вычислительным концентраторам напряжений. Гексаэдральные элементы менее чувствительны к форме и, как следствие, устойчивы к появлению вычислительных концентраторов. Однако при конечно-элементном анализе геометрически сложных тел дискретизация с помощью гексаэдральных элементов не всегда возможна, и чаще всего применяются тетраэдрические элементы. При этом стоит отметить, что для оценки сеточной сходимости необходимо провести множественные вычисления при разной степени дискретизации [33; 34] . Это означает, что при использовании тетраэдрических элементов для сеточной сходимости необходимо значительно густить сетку, что, в свою очередь, увеличивает время вычислений.

Применение аддитивных технологий в медицине позволило создавать изделия, сочетающие в себе решетчатые структуры, оболочки и объемные элементы [35; 36] . Однако при численном анализе таких изделий возникают определенные трудности. Это связано с совместным использованием балочных, оболочечных и твердотельных элементов. При численном моделировании таких изделий необходимо учитывать не только особенности построения конечно-элементной сетки, но и согласование степеней свободы в стыковых узлах. Например, при моделировании стыка балочного (6 степеней свободы) и твердотельного (3 степени свободы) элементов необходимо ограничить узел стыка, исключив степени свободы, связанные с поворотами. Это необходимо для того, чтобы узел стыка не был шарнирным. Другой особенностью моделирования таких конструкций является несоответствие жесткостей различных типов элементов, что приводит к возникновению ложных концентраторов напряжений.

Таким образом, при численном моделировании изделий, изготовленных аддитивным способом, необходимо найти баланс между точностью и временем вычислений. Ранее авторами была опубликована работа, посвященная экспериментальному исследованию изгибной жесткости решетчатого метаматериала [37]. Целью же данного исследования является получение конечно-элементной модели для моделирования напряженно-деформированного            состояния метаматериала,        предназначенного        для интрамедуллярного штифта.

Материалы и методы

Описание работы

В качестве исследуемого объекта была выбрана решетчатая структура третьего типа из опубликованной авторами работы [37] . Образец исследовался на четырехточечный изгиб с помощью численных и натурных экспериментов.

Численные эксперименты проводились для пяти КЭ-моделей. Каждая КЭ-модель характеризуется различными типами элементов, используемых для моделирования внешних ребер, внутренней канюли и плеч нагружения. Наборы КЭ-моделей составлялись из балочных, оболочечных и твердотельных элементов. Для каждой КЭ-модели проводилась сеточная сходимость, для этого оценивались величины эквивалентных напряжений по Мизесу в трех характерных точках изделия, а также оценивалась результирующая реакция. После проведения сеточной сходимости были реализованы численные эксперименты для всех моделей.

Для верификации численных экспериментов проводились натурные испытания для решетчатого и сплошного образцов. Всего было изготовлено пять образов решетчатого типа и пять сплошного. Изготовление осуществлялось методом лазерной стереолитографии на фотополимерном принтере без постполимеризации.

Описание геометрии решетчатого образцаи его производства

Объектом данного исследования является решетчатый образец (рис. 1). Ранее авторами были про-

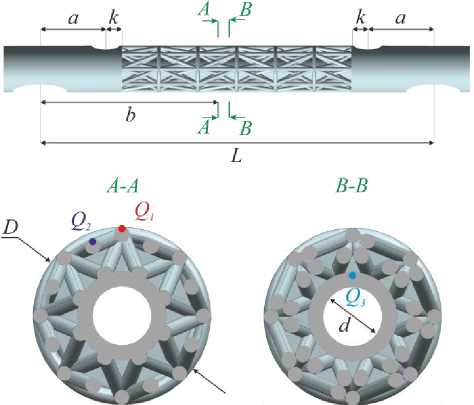
Рис. 1. CAD модель решетчатого образца ведены натурные испытания трех видов решетчатых структур [37]. Решетчатые образцы состоят из внешних ребер, внутренней канюли, предназначенной для установки интрамедуллярного штифта, и плеч нагружения. В данной работе рассматривается образец третьего типа. Геометрические параметры образца представлены в работе [37].

Исследуемые объекты изготавливались методом лазерной стереолитографии на фотополимерном принтере Anycubic Photon Mono X (Китай). Использовалась фотополимерная смола Anycubic Colored UV Resin Grey (Китай), характеристики которой приведены в табл. 1. Толщина слоя печати 10 мкм. Решетчатые образцы изготавливались в количестве пяти штук. Дополнительно были изготовлены контрольные сплошные образцы. В отличие от прошлого исследования [34] , образцы не подвергались постполимеризации ультрафиолетом.

Описание численных экспериментов

В данном исследовании используются пять КЭ-моделей для определения напряженно-деформированного состояния решетчатых образцов. При дискретизации первой модели внешние ребра, внутренняя канюля и плечи решетчатого образца были смоделированы в виде одномерных балочных элементов (модель beam-beam-beam ). В отличие от первой, вторая модель предполагает использование оболочечного элемента для внутренней канюли (модель beam-shell-beam ). У третьей модели внутренняя канюля моделировалась твердотельным элементом (модель beam-solid-beam ). Четвертая модель представляла собой балочные элементы, моделирующие решетчатую структуру, оболочечные элементы для внутренней канюли и твердотельные элементы для плеч решетчатого образца (модель beam-shell-solid ). Пятая модель состояла только из твердотельных элементов (модель solid-solid-solid ).

Для численного моделирования напряженно-деформированного состояния сплошного образца была выбрана только модель beam-beam-beam .

Таблица 1

Характеристики фотополимерной смолы Anycubic Colored UV Resin

Наименование	Величина
Модуль упругости, МПа	1400 – 1600
Прочность на растяжение, МПа	23,4
Коэффициент Пуассона	0,3

Во всех моделях механическое поведение метаматериала можно описать линейной постановкой задачи теории упругости:

V o = 0                V x , у , z e V ,	(1)
T £ = 1( V U +V U )     V x , у , z e V , 2	(2)
o = E : £                V x , у , z e V ,	(3)
где V - расчетная область, o - тензор	напряжений,

£ - тензор деформаций, e - тензор упругости второго ранга, и - вектор перемещения.

Схемы нагружения при конечно-элементном моделировании       напряженно-деформированного состояния для всех моделей представлены на рис. 2. Зеленым цветом на рис. 2, а, представлены узлы, к которым применялась жесткая связь. Соединения, которые моделировались с помощью жестких связей, обозначены красными линиями на рис. 2. Фиолетовым цветом на рис. 2 представлены узлы, которые стыковали балочные или оболочечные элементы с твердотельным элементом. Желтым цветом на рис. 2 отмечены узлы, которые стыковали балочные и оболочечные элементы.

Граничные условия (ГУ) приняты двух типов. У первого типа в узле А перемещение фиксирует шарнирная-неподвижная опора, у второго типа шарнирно-подвижная (см. рис. 2, а ).

Модель beam-beam-beam

При     конечно-элементном     моделировании использовались: одномерные трехузловые конечные элементы с квадратичной аппроксимацией. Соединение ребер и канюли моделировалось с помощью жестких связей (красный цвет на рис. 2, а).

Граничные условия численной модели решетчатого образца при шарнирно-неподвижной опоре в узле A представлены формулами (4) и (5), где и - вектор перемещения.

U(х*) = 0, x* = 0, x* = L;(4)

Uk (x*)=( 0; —1;0) мм, x*=a, x=L - a.

Граничные условия численной модели решетчатого образца при шарнирно-подвижной опоре в узле A представлены формулами (6)-(8):

U(x*) = 0, x* = 0;(6)

U kxx*)=( 0; —1;0) мм, x*=a, x*=L - a;

U(x*) = (Vx; 0; 0), x*=L.(8)

Граничные условия жестких связей представлены формулой (9):

U (in)=U (zn)=U (jn), n=rm.

Модель beam-shell-beam

При конечно-элементном анализе второй модели использовались: одномерные трехузловые конечные элементы с квадратичной аппроксимацией для ребер и плеч (см. рис. 2, б) . Оболочечным элементом моделировалась канюля. Соединения ребер с плечами и канюли с плечами осуществлялось с помощью жестких связей (красный цвет на рис. 2, б ). Соединения ребер и канюли моделировалось соединением общих узлов «стык в стык» (желтый цвет на рис. 2, б ).

Граничные условия при шарнирно-неподвижной опоре представлены формулами (4), (5) и (9). Для модели с шарнирно-подвижной опорой граничные условия представлены формулами (6)-(9).

Модель beam-solid-beam

Для третьей модели использовались: одномерные трехузловые конечные элементы с квадратичной аппроксимацией для ребер и плеч. Твердотельным гексаэдральным элементом моделировалась канюля. Схема нагружения представлена на рис. 2, в . Отдельно для всех узлов t n , стыкующих балочные с твердотельными элементами (фиолетовый цвет на рис. 2, в ), применялись граничные условия на фиксацию углов поворота:

■ у '( x\t_n ); y *( t„ ); z\t_n )) = 0

■ x '( x*(t ); y*(t ); z*(t )) = 0. (io)

nnn z'(x*(t); y*(t); z*(t)) = 0

nnn

Граничные условия для третьей модели при шарнирно-неподвижной опоре представлены формулами (4), (5), (9) и (10). Для модели с шарнирноподвижной опорой граничные условия представлены формулами (6)-(10).

Модель beam-shell-solid

Для ребер четвертой модели использовались трехузловые конечные элементы с квадратичной аппроксимацией. Канюля моделировалась оболочечным элементом. Плечи моделировались твердотельным гексаэдральным элементом. Для всех узлов t n , стыкующих балочные и оболочечные элементы с твердотельным элементом (фиолетовый цвет на рис. 2, г ), применялись граничные условия на фиксацию углов поворота, представленные формулой (10).

Граничные условия численной модели решетчатого образца при шарнирно-неподвижной опоре в узле A представлены формулами (10) и (11).

x * = 0, x * = L,

U ( x *; y *; z *) = 0, y * =-Д y ,                   (11)

z * e [ - D /2; D /2].

Граничные условия численной модели решетчатого образца при шарнирно-подвижной опоре в узле A представлены формулами (10), (12) и (13).

х * = 0,

U ( х *; y *; z *) = 0, у * =-Д у ,                    (12)

z * e [ - D /2; D /2].

х * = L ,

U ( х *; y *; z *) = ( V х ;0;0), y * =-Д y ,                (13)

z * е [ - D /2; D /2].

Модель solid-solid-solid

При конечно-элементном анализе пятой модели использовались только твердотельные тетраэдрические элементы (см. рис. 2, д). Граничные условия численной модели решетчатого образца при шарнирнонеподвижной опоре в узле A представлены формулой (11), при шарнирно-подвижной опоре в узле A представлены формулами (12), (13).

метаматериала была исследована сеточная сходимость для пяти конечно-элементных моделей при кинематической нагрузке 0,5 мм. Для этого были выбраны три узла, принадлежащие точкам Q 1 , Q 2 , Q з (см. рис. 1), в которых определялись эквивалентные напряжения по Мизесу.

Кроме того, исследовалась зависимость результирующей реакции от размера элемента конечно -элементной сетки. Выбор указанных узлов был обусловлен их расположением в зонах, удаленных от областей приложения граничных условий.

Сеточная сходимость конечно-элементной модели исследовалась при модуле упругости, полученного в ходе обработки данных натурных испытаний сплошных образцов.

Описание натурных экспериментов

Изготовленные образцы испытывались под действием четырехточечного изгиба. Испытания образцов осуществлялись до достижения фиксированного перемещения подвижной траверсы разрывной машины, установленного на уровне 3 мм. Расчет изгибной жесткости образца производился согласно классической теории балок по формуле:

Fa ² z х z х

EJ = Fa (3 L - 4a ), (14) zz 6 U ( a )

Сеточная сходимость

где E - модуль упругости, J zz

–

момент инерции

поперечного сечения, U - перемещение, L , a - линейные размеры образца, указанные на рис 1.

Для численной деформированного напряженнорешетчатого оценки состояния

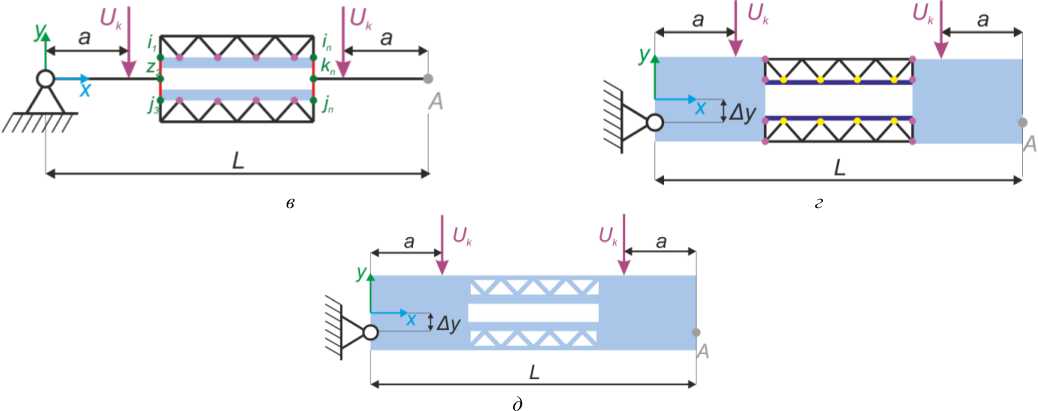
Рис. 2. Схемы нагружения для рассматриваемых конечно-элементных моделей: а - beam-beam-beam ; б - beam-shell-beam ; в - beam-solid-beam ; г - beam-shell-solid ; д - solid-solid-solid

Для метаматериала и сплошных образцов определялись усилия при перемещении подвижной траверсы на 0,5 мм. Для сплошного образца дополнительно определялся модуль упругости по формуле (14). Для этого в ходе натурных экспериментов определялось соотношение F/U путем определения линейного участка на диаграмме нагружения. Результаты распределения полученных модулей упругости и усилий при перемещении на 0,5 мм представлены в виде M (P2; P3), где M – медиана, P2, P3 – 25-й и 75-й процентили соответственно. Схема нагружения, анализ данных и процесс проведения натурных экспериментов представлен в работе [34].

Результаты

Натурные эксперименты

Характерные диаграммы нагружения для сплошного и решетчатого образцов представлены серыми кривыми на рис. 3, а и б соответственно. Линейный участок (красный цвет на рис. 3) определялся на интервале перемещения от 0 до 0,5 мм. Медианное значение модуля упругости сплошного образца составило 547 (485; 570) МПа.

Медианное усилие при кинематической нагрузке 0,5 мм, для цилиндрического образца составляло 50 (43,5; 51) Н. Для метаматериала медианное значение усилия, при перемещении подвижной траверсы испытательной машины на 0,5 мм, составляло 12 (12; 13,5) Н.

Сеточная сходимость

Сеточная сходимость и последующие численные эксперименты были выполнены на компьютере с процессором Intel Core i7 8700 (6 ядер, частота 3,2 ГГц), оперативной памятью 64 ГБ (частота 2600 МГц) и видеокартой NVIDIA GTX 1070 Ti .

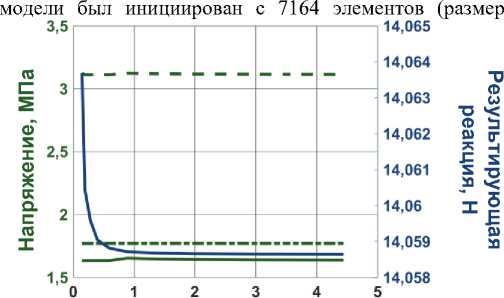
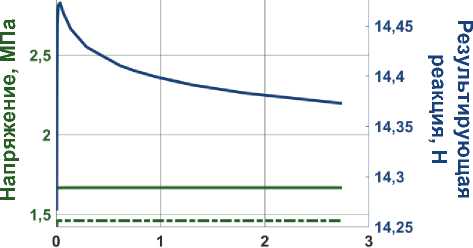
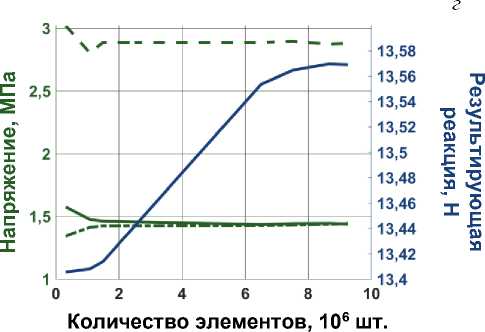
Сеточные сходимости в узлах, принадлежащим точкам Q1, Q2, Q3, для всех КЭ-моделей представлены на рис. 4 сплошной, пунктирной и штрихпунктирной зелеными кривыми соответственно. Зависимости результирующей реакции от количества элементов представлены на рис. 4 синими кривыми.

Модель beam-beam-beam

Анализ сеточной сходимости численной модели был начат с размера конечного элемента 2,5 мм. Так, численная модель состояла из 1438 элементов (см. рис. 4, а ). Определено, что при сгущении КЭ-модели до 44 432 элементов (размер элемента 0,065 мм) напряжения в исследуемых узлах и результирующая реакция изменялись менее 0,3 %, по сравнению с начальной КЭ-сеткой. Время расчета густой сетки составило 3 с.

Для последующего сопоставления численных и экспериментальных данных было выбрано 19 920 элементов, что соответствует размеру конечного элемента 0,146 мм. Время расчета 1 с.

Модель beam-shell-beam

Исследование сеточной сходимости второй численной модели было инициировано с 3582 элементов, что соответствует размеру конечного элемента 1,178 мм (см. рис. 4, б ). Результирующая реакция в опорах и напряжения в исследуемых узлах, принадлежащих точкам Q 1 , Q 2 , Q 3 , при увеличении количества элементов до 2 741 882 (размер элемента 0,021 мм) изменялись менее чем на 3 %, по сравнению с начальной КЭ-сеткой. Время расчета густой сетки составило 189 с.

Для верификации численных и экспериментальных данных было выбрано 290 968 элементов (размер конечного элемента 0,069 мм). Время расчета составило 14 с.

Модель beam-solid-beam

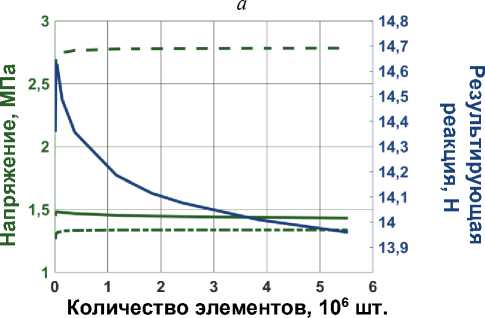
Исследование сеточной сходимости численной модели beam-solid-beam было начато с применения сетки, состоящей из 9294 элементов (см. рис. 4, в). Размер конечного элемента в начальной КЭ-модели

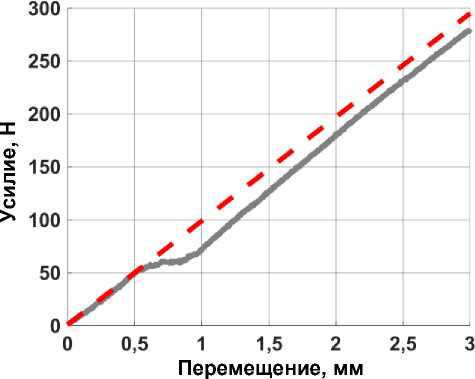
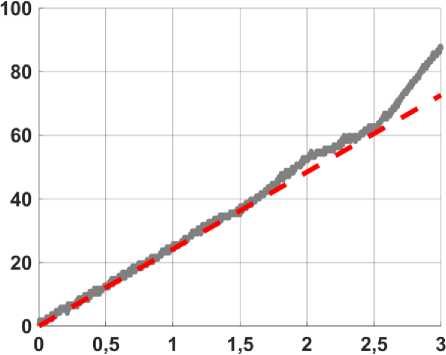
Перемещение, мм

а                                                    б

Рис. 3. Диаграмма нагружения: а – сплошной образец; б – решетчатый образец

составлял 0,79 мм. Напряжения в исследуемых узлах и конечного элемента 1,178 мм). Результирующая реакция результирующая реакция при увеличении количества элементов до 5 528 958 (размер конечного элемента 0,06 мм) изменялись менее чем на 7 %, по сравнению с начальной КЭ-сеткой. Время расчета густой сетки составило 1158 с.

Для последующего сопоставления численных и экспериментальных данных было выбрано 1 163 166 элементов, что соответствует размеру конечного элемента, равному 0,1 мм. Время расчета 524 с.

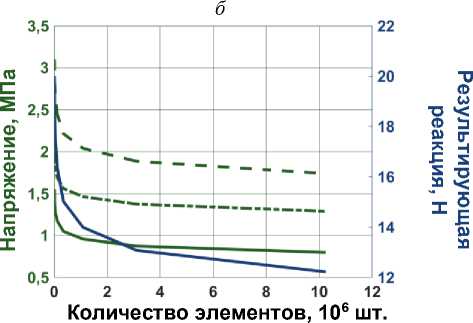
Модель beam-shell-solid и напряжения в исследуемых узлах, принадлежащих точкам Q1, Q2, Q3, при увеличении количества элементов до 10 238 928 (размер конечного элемента 0,07 мм) изменялись более чем на 48 %, по сравнению с начальной КЭ-сеткой (см. рис. 4, г). Время расчета густой сетки составило 3031 с.

Для последующего сопоставления численных и экспериментальных данных было выбрано 3 106 504 элемента, что соответствует размеру конечного элемента, равному 0,1 мм. Время расчета 651 с.

Анализ сеточной сходимости четвертой численной

3__ ___L _ _______ 14,5

Количество элементов, 104 шт.

Количество элементов, 106 шт.

д

Рис. 4. Сеточная сходимость моделей: а – beam-beam-beam ; б – beam-shell-beam ; в – beam-solid-beam ;

г – beam-shell-solid ; д – solid-solid-solid. Синим цветом показана величина результирующей реакции, зеленым – эквивалентные напряжения по Мизесу: точка Q 1 – пунктирная линия, точка Q 2 – сплошная линия и точка Q 3 – штрихпунктирная линия

Модель solid- solid-solid

Для пятой КЭ-модели процесс исследования сеточной сходимости начинался с 306 868 элементов, что соответствует размеру конечного элемента 0,7 мм (см. рис. 4, д ).

Напряжения в исследуемых узлах и результирующая реакция при увеличении количества элементов до 9 252 024 (размер конечного элемента 0,175 мм) изменялись менее чем на 9 %, по сравнению с начальной КЭ-сеткой. Время расчета густой сетки составило 1351 с

Для верификации численных и экспериментальных данных было выбрано 6 504 432 элементов (размер конечного элемента 0,2 мм). Время расчета 331 с.

Численные результаты

При конечно-элементном анализе использовался модуль упругости, полученный из данных натурных экспериментов сплошных образцов. Результаты численных экспериментов представлены для размеров элементов, принятых исходя из сеточной сходимости.

Результирующая реакция для сплошных образцов составила 46,4 Н при кинематической нагрузке в 0,5 мм.

Шарнирно-неподвижная опора

Результирующая реакция в первой конечноэлементной модели составляла 14,06 Н, когда у второй модели достигала 14,43 Н. Для третьей численной модели сумма реактивных сил достигла 14,19 Н. Наименьшее значение результирующей реакции при шарнирно-неподвижном закреплении составило 13,08 Н и было получено для четвертой конечно-элементной модели. Наибольшее значение результирующей реакции при шарнирно-неподвижном закреплении составило 21,96 Н и было получено для пятой численной модели.

Эквивалентное напряжение по Мизесу в узле, принадлежащем точке Q 1 , для первой конечноэлементной модели составило 3,12 МПа. Значение эквивалентного напряжения по Мизесу, зарегистрированное для второй модели, составило 2,97 МПа. В третьей модели напряжение достигло 2,78 МПа. Наименьшее значение эквивалентного напряжения по Мизесу наблюдалось для модели beam-shell-solid , где оно составило 1,88 МПа. Напряжение в пятой конечноэлементной модели было максимальным и достигло 7,12 МПа. Напряжения, для узлов принадлежащих точкам Q 2 и Q 3 , а также результирующая реакция для моделей с шарнирно-неподвижной опорой, представлены в табл. 2.

Шарнирно-подвижная опора

При конечно-элементном моделировании плеч с использованием одномерных балочных конечных элементов было установлено, что значения реактивных сил и эквивалентных напряжений по Мизесу, полученных при шарнирно-подвижном и шарнирно- неподвижном закреплениях, совпадают с точностью до седьмого знака после запятой.

Результирующая реакция для четвертой конечноэлементной модели составила 5,53 Н. Но при использовании только твердотельных элементов ( solid-solid-solid ) результирующая реакция была ближе к первым трем моделям и составляла 13,55 Н.

Эквивалентное напряжение по Мизесу в узле, принадлежащем точке Q 1 , для четвертой конечноэлементной модели составляла 1,18 МПа. Аналогичная величина для модели solid-solid-solid составляла 2,89 МПа.

Напряжения для узлов, принадлежащих точкам Q 2 и Q 3 , а также сумма опорных реакций для моделей с шарнирно-подвижной опорой представлены в табл. 2.

Обсуждение

При численных экспериментах использовался медианный модуль упругости, определенный по данным натурных экспериментов [37] . Межквартильный размах модуля Юнга составил 85 МПа (15 %). Аналогичный размах упругих свойств фотополимерных материалов отмечается и другими авторами [38; 39] . Величина размаха связана не только с особенностями технологии производства, но и с дефектами, возникающими при изготовлении. Для сплошного образца значение результирующей реакции, полученное в результате численного моделирования при кинематической нагрузке в 0,5 мм, оказалось на 7 % ниже медианного экспериментального значения, установленного в ходе натурных испытаний. При этом необходимо отметить, что результаты численных расчетов находились внутри доверительного интервала результатов натурных экспериментов. Для решетчатых образцов величина результирующей реакции, полученная в ходе численных экспериментов для всех моделей, получилась завышенной, в сравнении с данными натурных экспериментов. Модель beam-shell-solid показала наиболее близкое к экспериментальным значение результирующей реакции. Кроме того, значение результирующей реакции, полученное с помощью модели beam-shell-solid , находятся внутри доверительного интервала аналогичной величины, определенной по данным натурных экспериментов. Несмотря на то, что модель beam-shell-solid показала наилучшее совпадение с данными эксперимента, стоит, во-первых, отметить длительное время расчета (от 651 до 3031 с), а во-вторых, чувствительность к граничным условиям. Так, при различных формах шарнирного закрепления результирующая реакция варьировалась на 57 %. Чувствительной к граничным условиям оказалась модель solid-solid-solid (38 %). Для обоих типов граничных условий результирующая реакция была завышена. Модели beam-beam-beam , beam-shell-beam и beam-solid-beam были устойчивы к граничным условиям. Характер чувствительности к граничным условиям в различных моделях сохранялся и для эквивалентных напряжений по Мизесу.

Таблица 2

Результаты численных расчетов

Модель	Напряжение в узле, принадлежащему точке Q 1 , МПа		Напряжение в узле, принадлежащему точке Q 2 , МПа		Напряжение в узле, принадлежащему точке Q 3 , МПа		Результирующая реакция, Н
	Шарнирно неподвижная опора	Шарнирно подвижная опора	Шарнирно неподвижная опора	Шарнирно подвижная опора	Шарнирно неподвижная опора	Шарнирно подвижная опора	Шарнирно неподвижная опора	Шарнирно подвижная опора
beambeambeam	3,12	3,12	1,64	1,64	1,77	1,77	14,06	14,06
beamshellbeam	2,97	2,97	1,67	1,67	1,46	1,46	14,43	14,43
beamsolidbeam	2,78	2,78	1,45	1,45	1,34	1,34	14,19	14,19
beamshellsolid	1,88	1,18	0,88	0,61	1,38	0,62	13,08	5,53
solidsolidsolid	7,12	2,89	1,80	1,44	2,22	1,43	21,96	13,55

Здесь можно выделить преимущества модели beam-beam-beam . Во-первых, эта модель устойчива к граничным условиям. Во-вторых, имеет минимальное время расчета и, следовательно, не требует высокой производительности вычислительной машины, что, в свою очередь, позволяет произвести комплекс численных экспериментов (изгиб, сжатие, растяжение). В-третьих, обеспечивает наиболее быструю сходимость сетки. Однако эта модель имеет ограничения с точки зрения области применимости: будет неоправданно для ортопедических конструкций не балочного типа.

Поскольку поведение конечно-элементных моделей описывается линейной постановкой задачи теории упругости, численные результаты зависят от заданного модуля упругости. При условии, что модуль упругости, определённый в натурных испытаниях, соответствует 75-му квартилю, относительная погрешность численной модели для сплошного образца составляет 3–4 %. Однако в этом случае результирующая реакция для всех решетчатых моделей возрастёт, что приведет к увеличению запасу прочности по сравнению с реальным поведением метаматериала, что, в свою очередь, с одной стороны, повышает надежность реальной конструкции, а с другой стороны, снижает оптимальность распределения материала.

При этом необходимо отметить, что конечноэлементные модели решетчатой структуры с использованием медианного значения модуля упругости уже приводят к завышенной оценке результирующей реакции. Из-за наличия данных особенностей необходимо проводить серию натурных испытаний для уточнения физико-механических характеристик материалов, изготовленных аддитивным способом.

Заключение

Работа посвящена численному моделированию решетчатых изделий, изготовленных аддитивным способом. Объектом исследования выступал метаматериал, обладающий решетчатой структурой. В работе было представлено пять конечно-элементных моделей, состоящих из балочных, твердотельных и оболочечных элементов с разными видами граничных условий. Для всех конечно-элементных моделей выполнялась сеточная сходимость с оценкой напряжений по Мизесу и результирующей реакции. Результаты численного моделирования сравнивались с данными экспериментов, для оценки качества использовалась результирующая реакция. В расчетах использовался модуль упругости из натурных экспериментов сплошных образцов.

В ходе численных экспериментов для решетчатых образцов значения результирующей реакции оказались завышенными по сравнению с данными, полученными в ходе натурных испытаний. Наиболее точное согласование с экспериментальными результатами продемонстрировала смешанная модель, состоящая из балочных, оболочечных и твердотельных элементов. Значение результирующей реакции, полученное с использованием данной модели, находилось в пределах доверительного интервала данных натурных экспериментов. Но при этом авторы считают, что баланс между точностью и временем вычислений показала модель, состоящая только из балочных элементов.

Полностью    твердотельная    модель    оказалась чувствительной к граничным условиям, при этом результирующая реакция возрастала вплоть до 38 %.

Полученные результаты подчеркивают особенность численного моделирования нерегулярных пористых изделий и важность верификации численных моделей с данными натурных испытаний. Так, сеточная сходимость наблюдалась во всех моделях, но сравнение с данными натурных экспериментов показывает значительное отклонение расчетных величин от реальных.