Численное исследование сезонных вариаций глобальной системы нейтрального ветра в средней атмосфере Земли

Численная глобальная модель циркуляции нижней и средней атмосферы Земли была недавно разработана в Полярном геофизическом институте [1, 2]. Эта модель основана на численном решении системы нестационарных трехмерных уравнений Навье– Стокса и неразрывности для сжимаемого вязкого газа. Модель позволяет рассчитывать трехмерные глобальные распределения зональной, меридиональной и вертикальной компонент скорости нейтрального ветра и плотности воздуха на уровнях тропосферы, стратосферы, мезосферы и нижней термосферы Земли без каких-либо ограничений на вертикальный перенос атмосферного газа. Ранее модель уже применялась для исследования влияния горизонтальной неоднородности температуры атмосферы на глобальную циркуляцию средней атмосферы для периода времени, когда в Северном полушарии лето [1, 2]. В настоящей работе эта модель применяется для расчета крупномасштабной циркуляции земной атмосферы для условий четырех различных сезонов.

Математическая модель

Применяемая в настоящей работе модель имеет два существенных отличия от других моделей общей циркуляции атмосферы. Во-первых, в ней температура воздуха не рассчитывается, а является входным параметром модели и задается по какой-либо эмпирической модели. Описываемые в настоящей работе результаты расчетов получены при температуре, задаваемой по эмпирической модели NRLMSISE-00 [3]. Такой способ задания температуры обусловлен следующими обстоятельствами. Известно, что главным фактором, определяющим циркуляцию атмосферы, является ее неравномерный нагрев из-за процессов поглощения атмосферными газами электромагнитного излучения Солнца, излучения земной поверхности и излучения самой атмосферы, а также из-за процессов излучения энергии атмосферными газами в инфракрасном диапазоне. В этих процессах главную роль играют малые приме- си, которые излучают и поглощают энергию в большом количестве спектральных интервалов и участвуют в многочисленных фотохимических и химических реакциях. Для полного описания этих процессов необходимо решать самосогласованную систему, в которую входят уравнения движения, уравнение переноса электромагнитного излучения, уравнение энергии и уравнения для малых примесей с учетом химических реакций и турбулентного переноса. На высотах 20–80 км сечения некоторых процессов излучения – поглощения и константы скоростей некоторых фотохимических реакций известны пока недостаточно точно. Экспериментальное определение указанных параметров атмосферных фотохимических реакций сильно усложняется тем, что многие из этих реакций невозможно воспроизвести в наземных лабораториях. Поэтому расчет нагрева атмосферы на высотах 20–80 км с достаточной точностью является трудно выполнимой задачей. Неточность в расчете температуры воздуха может привести к качественно неверной картине циркуляции атмосферы. В силу изложенных причин задание температуры по эмпирической модели NRLMSISE-00, которая построена по статистически осредненным экспериментальным данным и верно отражает реальную зависимость температуры воздуха от высоты, широты и долготы, представляется авторам оправданным.

Во-вторых, в применяемой в настоящей работе модели вертикальная скорость газа находится не из условия гидростатического равновесия, а путем численного решения полного уравнения движения для вертикальной составляющей скорости без пренебрежения какими-либо членами. Таким образом, все три компоненты скорости рассчитываются при помощи численного решения полных уравнений движения вязкого сжимаемого газа. При этом не используется уравнение гидростатики, обычно применяемое в моделях общей циркуляции атмосферы. Применение уравнения гидростатики в моделях общей циркуляции атмосферы приводит, как известно, к тому, что рассчитываемые по таким моделям вер- тикальные скорости обычно не превышают 1 м/с. В то же время имеются экспериментальные данные о том, что в высоких широтах в средней и верхней атмосфере наблюдаются большие (до 100 м/с) значения вертикальной компоненты скорости нейтрального ветра [4–7], которые не могут быть получены при помощи моделей, базирующихся на уравнениях гидростатики.

Таким образом, применяемая модель основана на численном решении полной системы уравнений движения вязкого сжимаемого газа, состоящей из уравнения неразрывности и трех полных уравнений для вертикальной, зональной и меридиональной компонент гидродинамической скорости без каких-либо упрощений. Для решения уравнений применяется метод конечных разностей. Областью расчетов является окружающий Землю слой, простирающийся от земной поверхности до высоты 126 км над экватором. Земная поверхность считается сплюснутым с полюсов эллипсоидом вращения. Верхняя граница области моделирования является сферой, проходящей на высоте 126 км над экватором. Расчетная сетка является равномерной по долготе и широте и имеет по этим измерениям одинаковый шаг, равный 1 ° . По высоте расчетная сетка неравномерна, ее шаг не превышает 1 км. Влияние турбулентности, имеющей масштабы меньшие шагов расчетной сетки, на среднее течение атмосферного газа принимается во внимание, для параметризации этой турбулентности используется одна из существующих эмпирических моделей. Граничные условия задавались так, чтобы выполнялся закон сохранения массы в области расчетов. Детальное описание применяемой математической модели можно найти в работах [1, 2].

Результаты расчетов и их обсуждение

Применяемая математическая модель способна учитывать различные комбинации солнечной и магнитной активностей, а также разные сезоны. В настоящей работе расчеты выполнялись для условий, соответствующих четырем различным дням, относящимся к разным сезонам, а именно для 16 января, 16 апреля, 16 июля и 16 октября. Все расчеты были проведены для невысокой солнечной ( F _10.7= 101) и низкой магнитной ( K _p=1) активностей. Для каждого из четырех дней был взят один и тот же момент времени UT=10:30 и для этого момента были рассчитаны методом установления глобальные распределения зональной, меридиональной и вертикальной компонент скорости и плотности нейтрального газа. Задаваемые пространственные распределения температуры, вычислявшиеся по эмпирической модели NRLMSISE-00 в момент UT=10:30 для каждого дня, считались неизменными во времени, так же как и граничные условия.

Результаты расчетов, которые частично представлены на рисунке а–г, позволили установить следующие закономерности глобальной циркуляции атмосферы. Оказалось, что, несмотря на существенные различия в распределениях задаваемой по эмпирической модели NRLMSISE-00 температуры, рассчитанные для разных сезонов глобальные распределения атмосферных параметров обнаруживают ряд общих черт. Видно, что во все сезоны горизонтальная компонента скорости нейтрального газа является сильно изменяющейся функцией широты, долготы и высоты. Горизонтальная скорость ветра может иметь сильно отличающиеся направления в близко расположенных точках. Существуют ограниченные по размерам горизонтальные области, в которых поле горизонтальной скорости имеет резкие градиенты. Вертикальная скорость нейтрального газа может иметь противоположные направления в горизонтальных областях, разной конфигурации. Горизонтальные области, в которых вертикальный ветер направлен вверх, характеризуются, как правило , большей протяженностью как по длине, так и по ширине . Горизонтальные области, в которых вертикальный ветер направлен вниз , обычно являются длинными, но узкими полосами. Максимальные абсолютные значения вертикальной скорости, направленной вверх, оказываются меньшими, чем у направленной

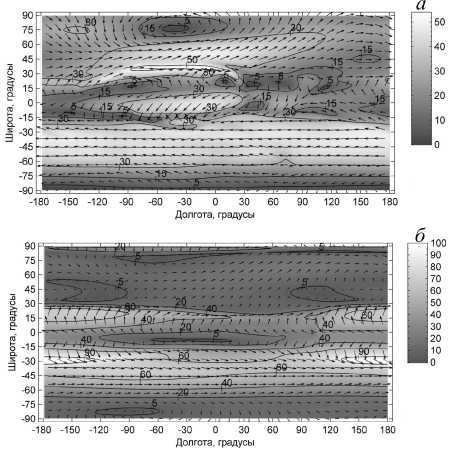
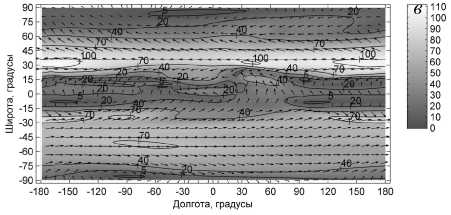
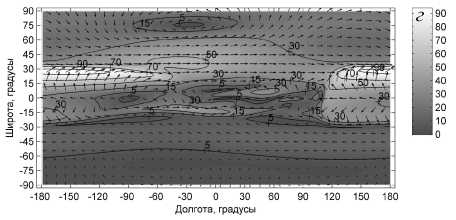
Распределение горизонтальной составляющей скоро сти ветра ( м / с ) на высоте 55 км , рассчитанное для 16 янва ря ( а ), 16 апреля ( б ), 16 июля ( в ) и 16 октября ( г ). Стрелки указывают направление , а их длина и линии уровня ука зывают величину скорости .

вниз скорости. Значения направленной вниз скорости могут достигать нескольких метров в секунду на высотах нижней термосферы в ограниченных по размерам узких длинных горизонтальных областях, совпадающих, как правило, с областями, в которых поле горизонтальной скорости имеет резкие градиенты.

Результаты расчетов, полученные при различных распределениях задаваемой по эмпирической модели NRLMSISE-00 температуры, взятых для разных дней, относящихся к разным сезонам, обнаруживают ряд существенных различий. Прежде чем рассмотреть эти различия, отметим следующий факт. Из многолетних наблюдений известно, что в периоды, свободные от стратосферных перестроек в атмосфере Земли, на уровнях стратосферы и мезосферы формируются симметричные относительно полюсов крупномасштабные вихревые движения – циркумполярные вихри (ЦПВ) Северного и Южного полушарий. В частности, в период, близкий к летнему солнцестоянию, в Северном полушарии формируется циркумполярный антициклон, а в Южном полушарии – циркумполярный циклон. В период, близкий к зимнему солнцестоянию, в Северном полушарии формируется циркумполярный циклон, а в Южном – циркумполярный антициклон.

Оказывается, что результаты расчетов, полученные для разных сезонов, существенно различаются между собой, в частности, характером циркумполярных вихревых движений. Из рисунка а можно видеть, что в январе в Северном полушарии сформировался циркумполярный циклон, а в Южном полушарии – циркумполярный антициклон. Рисунок в показывает, что в июле в Северном полушарии формируется циркумполярный антициклон, а в Южном полушарии – циркумполярный циклон. Видно, что для условий января и июля на уровнях стратосферы и мезосферы воссоздаются циркумполярные вихри, аналогичные тем, которые известны из наблюдений.

Рассмотрим результаты расчетов для условий апреля и октября. Из рисунка б видно, что при переходе от зимы к лету к середине апреля в Северном полушарии еще продолжает сохраняться ослабевший зимний циклон, а в Южном полушарии уже успевает произойти перестройка и сформироваться слабый циклон, который к лету значительно усиливается. Из рисунка г видно, что при переходе от лета к зиме к середине октября в обоих полушариях характерная для лета циркуляция разрушается и начинает зарождаться характерная для зимы циркуляция: в Северном полушарии сформировывается слабый циклон, а в Южном полушарии в мезосфере – слабый антициклон, значительно усиливающиеся к зиме.

Заключение

Разработанная ранее в Полярном геофизическом институте численная модель трехмерной системы нейтрального ветра в нижней и средней атмосфере была применена для расчета крупномасштабной циркуляции земной атмосферы для условий четырех различных сезонов. Результаты моделирования показали, что горизонтальная неоднородность температуры атмосферы, являющаяся различной в разные сезоны, оказывает существенное влияние на глобальную циркуляцию средней атмосферы, в частности, на формирование циркумполярных вихрей Северного и Южного полушарий. Во все сезоны рассчитанная по модели трехмерная крупномасштабная циркуляция средней атмосферы оказалась весьма неоднородной как в вертикальном, так и в горизонтальных направлениях. Для условий, когда в Северном полушарии лето или зима, на уровнях стратосферы и мезосферы воссоздаются циркумполярные вихри, аналогичные тем, которые известны из наблюдений. Этот факт свидетельствует об адекватности применяемой численной модели. Для условий, когда в Северном полушарии весна или осень, на уровнях стратосферы и мезосферы в расчетах получились некие средние между зимней и летней циркуляции, имеющие отдельные черты как той, так и другой.