Численное исследование сосуществования популяций в одной экологической нише

Имеются различные точки зрения на возможность присутствия нескольких близкородственных видов в одной экологической нише [1-4]. Принцип Гаузе [2] утверждает, что устойчивое сосуществование двух популяций невозможно, если ростограничен одним жизненно важным ресурсом. В то же время, известны примеры [3], когда в одной экологической нише обитают несколько близкородственных популяций. В [4] показано, что при моделировании с учётом нелинейности миграционных потоков возможна конкуренция биологических видов без вытеснения менее приспособленной популяции (обобщение принципа Гаузе).

В данной работе рассматривается модель, описывающая взаимодействие популяций хищников и жертв. Для решения системы нелинейных уравнений в частных производных применяется метод конечных разностей. Целью работы является моделирование сосуществования видов и определение параметров системы, при которых модель принадлежит классу косимметричных динамических систем [5, 6] с непрерывным семейством стационарных распределений [7].

Модель динамики конкурирующих популяций. Рассматривается модель взаимодействия двух популяций жертв и двух видов хищников, представляющая собой систему параболических уравнений [8, 9]. Для описания динамики близкородственных популяций аналогично [10] используется единая функция обобщённого ресурса (ёмкости среды) р^х.уу Изменение плотности популяций жертв определяется логистическим законом (параметры роста р_и р₂) и убылью из-за присутствия хищников (слагаемые с коэффициентами /,, / = 1...4)[1].

Работа выполнена при финансовой поддержке гранта РФФИ № 14-01-00470.

—- = k./\u, +f., Qt	j 4^i 4^2/
8u2 1 .      , —- = к2Ди2 +f2, Qt	,                U, + U2 ,          , f2 = P2U2 1 - —---- - 4^2^! ""  KU2W2i VP)              (1)
—- = kJ\w. -vL, Qt Qw. , д , -^ = /с4Ди/2+Г4, I Qt	/3=P3W1l/1+p4W1l/2-/5W1, fA = РзИ/,^ + р6И/2Ц2 - /6И/2.

Прирост плотности популяций хищников за счёт потребления жертв даётся слагаемыми с коэффициентами р,, / = 3... б, а естественная смертность — слагаемыми с коэффициентами /5, /6

• [11] . В (1) матрицы второго порядка к, состоят из диффузионных коэффициентов.

Рассматривается ареал в виде прямоугольника Q = [0,а] х [О,/?], на границах которого ставились условия отсутствия потоков [12]:

Vu,!(0,y,f) = Vu,! (a,y,t ) = Vu,₂(x,0,f) = Vu_/2 (x,b,t ) = 0, Vu_/2(x,0,f) = Vu_/2 (x,b,t ) = 0,

• Vn/_;1(0,y,f) = Vn/,₁(a,y,f) = 0, Vw,₂ (x,0,t) = Vw,₂ (x,b,t) = 0, / = 1,2.       ®

Система дополняется начальными распределениями для плотностей популяций:

и, (х,у,0) = и° (х,у,0), и/, (х,у,0) = w° (х,у,0), / = 1,2.                (3)

Рассматриваемая задача при определённых комбинациях параметров относится к классу косимметричных систем [5, 6], для которых возможно возникновение непрерывных семейств стационарных распределений популяций [13].

Анализ показывает, что система (1) — (3) обладает косимметрией вида

L = (Si^u2 .^А. ^2, ^4^1 Г,                            (⁴)

когда вещественные параметры q, связаны соотношениями, получающимися из условия ортогональности вектора L правой части системы (1) — (2). Рассматриваемая система обладает косимметрией [14] при выполнении соотношений:

^1^2 = —^2^1 ' М1^2 =      ' 4^2 = “4^1 ' 4^2 = “4^1

'                            (5)

К3Ч4 — К4Ч3 г М3Ч4 ^— М5Ч3 / М4Ч4 ^— МбЧз / '5Ч4 ^— 'бЧз ■

Так как косимметрия [10] определяется с точностью до постоянного множителя, то далее ^1 ⁼ “^2,11 ' ^3 ^{= —}^М,11 ■

Численный метод. Для решения задачи (1) — (3) применяется метод прямых с дискретизацией на основе смещённых сеток. По переменным хи увводятся равномерные сетки: xr = rhx, ys = shy, г _-1,0,...,лх +1, s = -1,0,...,^ +1, hx -afnx, hy =b/ny . Через uire (w//5) обозначается значение плотности распределения популяции и, (и/,) в узле (xr,ys). Для вычисления потоков вво дятся вспомогательные сетки: х,,12 = -hx / 2 + rhx, r = l,...,nx, ys+1/2 = -hy /2 +shy, s =1,...,пу.

ГТКРЫ1-1П

I DCnnUi

При аппроксимации уравнений (1) по пространственным переменным вводятся разностные операторы первого порядка на двухточечных шаблонах:

(H r.x\ - ^torA.s ^tor,s                 _ ^Wr,s+1 ^tor,s

В результате получается следующая система обыкновенных дифференциальных уравнений:

у, s = 0,...,n_y, s = 0,...,п , / = 1,2 .

u_i>re = Wi^un + ^dAu^ +/ L, г = о,..., л_; ^,_ге = [Ш + d₂d₂w.₂ + f_2;+1 ]_re, r = 0,..., n_x,:

Дискретные аналоги краевых условий (2) дают соотношения для величин в законтурных узлах:

U,,-1,S = и_1Д,₅, ил __1-s = w,_AiS, s = О,..., n_y,

u,r_Y=u,rY, vv Y — wjY, r = 0,...,n , i = l,l.

Из (3) следуют начальные условия для (6), (7):

и = и° (х ,у L /' = 1,2, w = w°(x L i = 1,2, r = 0,...,nx, s = 0,...,ny.

Система (6) — (8) записывается в виде:

Y = F^, y^ = y_q, Y = ^U_YIU_2lW_YIW₂j,

/,11' /,12'     • i _Yn ' /,21' /,22'    '

i = l,l,

И/ =1/1/ i/iz w w w w vvi \vvi,llivvi,XZi'"ivv • Xn fvv, n n где Yo — вектор начальных данных.

Для интегрирования по времени задачи Коши (9) применяется метод Рунге — Кутты четвёртого порядка.

Косимметрией системы (9) является дискретный аналог векторного поля L, получаемый из (4) — (5) в результате дискретизации. Поскольку нулевые решения задачи (9) (вектор Y = 0) аннулируют косимметрию, то любое ненулевое стационарное решение К (то есть F (К) = 0) не обнуляет косимметрию и, таким образом, принадлежит однопараметрическому семейству равновесий. При этом в спектре устойчивости равновесия Y, имеется нулевое значение, которое соответствует нейтральному направлению вдоль семейства. Если остальные спектральные величины лежат в левой полуплоскости, то равновесие Y, устойчиво. Это отвечает устойчивости в трансверсальном к семейству многообразии [5].

Численные результаты. Для прямоугольной области Q = [0,2] х [0,1] представлены результаты по исследованию стационарных распределений популяций жертв и хищников на прямоугольном ареале. Функция обобщённого ресурса р(х,у) соответствует наличию на ареале двух благоприятных зон (рис. 1). Расчёты проводились до выхода на устойчивые стационарные распределения.

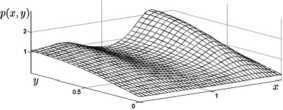
Рис. 1. Функция обобщённого ресурса р(х,к)

В вычислениях использовались раметры диффузии и роста-убыли:

следующие па

° )

0,04/

° Y o,osj'

ГО,03   0 )       Г 0,04

М 0  0,03/      0

ГО,06   О )        ГО,08

0   0,06/        О

Mi = 3, р2 = 4, м3 = 3, м4 = 1,2 , м5 = 4, м6 = 1,6;

4 =/2 =/5=о,9 4 =4 =4 =1,2.

В этом случае система (1) — (3) обладает косимметрией (4) — (5) и возникает непрерывное семейство стационарных распределений. Для аппроксимации кривой семейства было вычислено более сотни точек, каждая из которых отвечает решению системы (9). Расчёт семейства проводился методом, описанным в [13]. В спектре полученных стационарных распределений имеются практически нулевые собственные значении (о = 10 6). Это означает, что данные решения входят в нетривиальное семейство стационарных распределений. При указанных параметрах семейство состоит из устойчивых решений, одно из них приведено на рис. 2. В силу однородности диффузии, профили распределений популяций жертв повторяют функцию обобщённого ресурса (см. рис. 1). При этом суммарная плотность жертв меньше значений функции р(х,у^ в точках максимума и больше — в точках минимума.

Если условие косимметрии нарушено, то для постоянных по пространству параметров роста происходит вытеснение наименее приспособленной популяции и на ареале остаётся только один вид. Например, если м^ ц > p₂^ _п, то из двух популяций жертв выживает только и₁.

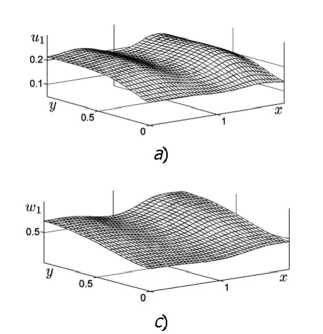
Рис. 2. Входящее в семейство стационарное распределение сосуществующих популяций жертв (а, В) и хищников (с, В)

Сосуществование популяций без выполнения условий косимметрии возможно также при неравномерных по ареалу параметрах роста и убыли. Далее представлены результаты для пере. 2пх _      ..

менного параметра роста популяции жертвы и2, задаваемого в виде р2 = р20 + ц21 sin---. В расче тах было фиксировано значение р20 = 4.

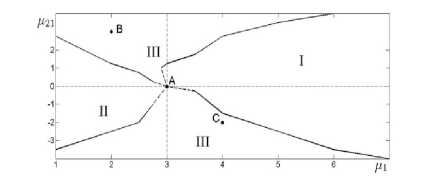
Рис. 3. Карта параметров, отвечающих сосуществованию (III) и выживанию жертвы u_v (I) или u₂ (II), точка А — существование непрерывного семейства решений

На рис. 3 дана карта режимов — плоскость параметров роста p_t и модуляции ц₂₁, которая состоит из трёх областей: две области соответствуют выживанию популяции и₁ или и₂, а третья является областью сосуществования видов. Точка А(3,0), к которой «стягиваются» области, отвечает случаю косимметрии и существованию семейства решений.

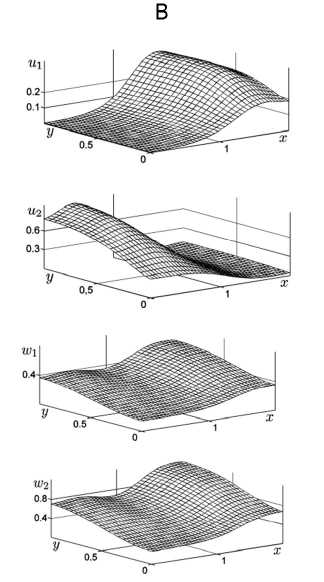
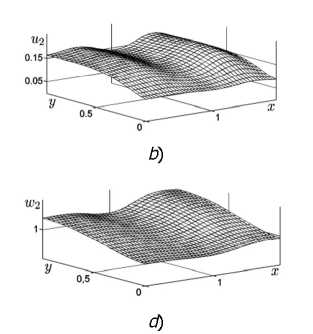
Рис. 4. Стационарные распределения сосуществующих популяций в случае неравномерного по пространству параметра роста р2: ц^ - 4, ц21 - 4 (столбец В); р^ = 4, ра = -3 (столбец С)

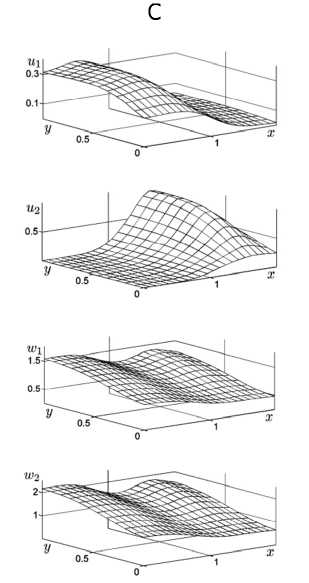
На рис. 4 приведены распределения популяций для параметров ц_т = 2, ц₂₁ = 4 и Mi = 4, ц₂₁ = -2 (точки В и С на рис. 3). В этих случаях наблюдается устойчивое сосуществование популяций жертв и хищников на ареале, но в силу неоднородности параметра роста ц₂ происходит размежевание популяций жертв. При ц₂₁ > 0 (точка В) популяция и₂ доминирует в подобласти х <а/2, а популяция ^ — в остальной части ареала. Плотности распределений популяций хищников в общем напоминают профиль популяции и₁, что связано с большими коэффициентами роста за счёт популяции и₁ . При ц₂₁< 0 (точка С) картина изменяется: теперь и₂ доминирует в подобласти х > а/2.

В случае неравномерности параметров роста хищников по ареалу, также реализуются сценарии сосуществования и вытеснения видов. Для неоднородного параметра роста

М₅ = р₅₀ + р₅₁ sin--- при фиксированном значении ц₅₀ = 4 на рис. 5 приведена карта режимов на 3

плоскости параметра ц3 и коэффициента модуляции р51. Карта состоит из трёх областей: области совместного существования хищников и областей выживания одного из хищников. Границы области стягиваются к точке, удовлетворяющей условию косимметрии (ц51 = 0, р3 = 3).

Заключение. Найдены условия на параметры системы, при которых модель принадлежит классу косимметричных динамических систем [10, И] и имеется непрерывное семейство стационарных распределений [14]. Предложена модель для описания взаимодействия популяций хищников и жертв на пространственно неоднородном двумерном ареале. Модель представлена в виде системы нелинейных уравнений параболического типа для двух близкородственных популяций хищников и двух популяций жертв, конкурирующих за общий ресурс.

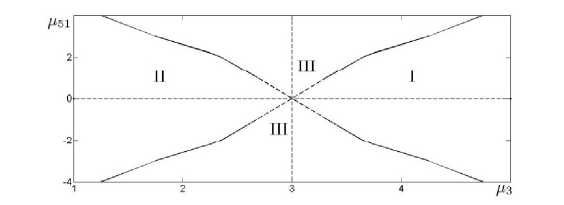
Рис. 5. Карта параметров, отвечающих сосуществованию (III) и выживанию одного их хищников ^ (I) и и/2 (II)

Показано, что при определённых соотношениях между параметрами и переменной по ареалу функции ресурса, задача принадлежит классу косимметричных динамических систем. В этом случае возникает непрерывное семейство стационарных распределений сосуществующих популяций. Вычислительный эксперимент основан на методе прямых и схеме смещённых сеток, аппроксимации построены с использованием метода баланса. Результаты демонстрируют возможности модели для описания формирования стационарных распределений популяций. Проанализированы условия сосуществования близкородственных видов, изучено формирование биологических структур при неоднородности параметров роста.