Численное исследование свободных колебаний лежащей капли

Исследования колеблющейся левитирующей капли в последнее время часто используются для определения физико-химических свойств жидкостей [1]. Обработка результатов почти всех таких экспериментов проводится на основании аналитической теории, предложенной в [2, 3] и пригодной для малых колебаний сферической капли идеальной жидкости в отсутствие объемных сил. Согласно [2] колебания формы капли описываются как г^в, 9,t^ = R-vs^Ylm^e, ф^.

где R - радиус равновеликой жидкой сферы, находящейся в равновесии, ¥1т - сферическая гармоника, е^ - гармоническая функция времени, s^ = A sin (си^ + ф}. Частоты колебаний капли согласно [2] описываются формулой й>„2=л(и-1)(й + 2)у-^, (1)

где л>2 - натуральное число, о - коэффициент поверхностного натяжения, М- масса капли. Основная частота колебаний получается при п = 2, при этом капля имеет вид эллипсоида вращения, отношение полуосей которого гармонически изменяется во времени.

Коэффициент затухания р для основной моды свободных колебаний капли, определенный как величина, обратная времени, в течение которого амплитуда колебаний уменьшается в е раз, определяется формулой [3]

где р - коэффициент динамической вязкости жидкости.

Существуют исследования, в которых формулы (1), (2) применяются для анализа колебаний лежащей [4] или подвешенной [5, 6] капли с целью определения поверхностного натяжения и вязкости жидкости. Для такого обобщения, однако, нет достаточных оснований. Во-первых, формулы (1), (2) получены при условии отсутствия массовых сил, а все эксперименты [4-6] проводятся в поле сил тяжести, во-вторых, присутствие твердой подложки неизбежно внесет асимметрию в течение жидкости внутри капли при колебаниях, и в-третьих, в [7] показано, что всякое отличие равновесной формы капли от сферической приводит к изменению и расщеплению частот колебаний. Следовательно, параметры свободных колебаний капли в поле силы тяжести, лежащей на твердой подложке, должны отличаться от таковых для свободных колебаний сферической капли, причем тем сильнее, чем капля крупнее. В [8] проведен анализ колебаний капли, зажатой между двумя плоскими поверхностями, и показана возможность определения вязкости и поверхностного натяжения в таком эксперименте. Анализ колебаний лежащей капли и сравнение их параметров (частоты и коэффициента затухания) с таковыми для свободной капли (1), (2) ранее не проводились и составляют цель настоящей работы.

Коренченко А.Е., Илимбаева А.Ж., Бескачко В.П.

Математическая модель и принятые приближения

Пусть капля находится на твердой горизонтальной подложке (рис. 1) в условиях, когда спра ведливы следующие приближения: 1) отсутствует испарение с поверхности жидкости, 2) имеет место осевая симметрия формы капли, распределений давления и течений в ней, 3) влиянием газовой среды на движение капли можно пренебречь, 4) тепловыделе

Рис. 1. Схема эксперимента

ние, обусловленное трением в жидкости, незначительно и им можно пренебречь, 5) жидкость несжимаема, 6) на твердой границе выполнено условие прилипания, 7) отсутствует гистерезис смачивания. Тогда уравнения движения жидкости в капле можно записать в виде:

9И                         8УД Э²У_г

--L —„M/.y)J7----|_р--г--LU--L--L

St '    * r р Sr yr Sr \ Sr ) Sz2 гД avz   /-      i sp  hsf зуд з2уД

St    '         p 8z   Д 8r\ dr ) Sz2 )

\d( SPA S2P ( (8УД2 (УД2 ДУг8Уг (ЭУ2

r Sr V Sr) Sz² V Sr ) V ^r ) Sr Sz у &

Уравнения (3) и (4) представляют собой уравнения Навье-Стокса, а (5) - уравнение Пуассона для давления. В (3)—(5) использованы следующие обозначения: V = {УГ, УД - вектор скорости, Р - давление сверх гидростатического, р, v - плотность и кинематическая вязкость жидкости, g - ускорение свободного падения.

В модели приняты следующие граничные условия:

• 1)    на твердой подложке равны нулю обе составляющие скорости: ^U=⁰’                      (6)

• 2)    касательное напряжение равно нулю в каждой точке границы раздела «жидкость-газ»:

  
  
  

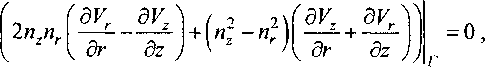
где п = Д_г,пД - вектор нормали к поверхности жидкости, Г- граница «жидкость-газ»,

• 3)    разность нормальных давлений определяется формулой Лапласа

( n п 2 ^9Уг n (ay_z ЭУД _{п 2} эуД

-7’ + 2hz/?v—r—2nznrpv —^ + —U2nrpv—-\ = стК,(8)

6г           у Sr Sz )8z )

здесь К - кривизна поверхности капли.

Для замыкания системы (3)—(8) в граничных ячейках записывается уравнение непрерывности

VV = 0.(9)

Уравнения (3)—(9) приводятся к безразмерной форме так, что все расстояния относятся к 7?, скорости - к v/R, давление - к pv²/R² , время - к Р²Д .

Численный метод решения

Для решения системы уравнений (3)-(9) использовалась разностная схема, построенная на основе равномерной пространственной сетки. Пространственные производные внутри капли аппроксимировались центральными разностями, на границе - односторонними. Временная производная вычислялась вперед по времени. Сетка перестраивалась на каждом временном шаге в соответствии с изменениями в форме капли. Системы линеаризированных разностных уравнений решались методом исключения Гаусса. При проведении тестовых расчетов шаг по времени и пространству уменьшался до тех пор, пока результаты не переставали зависеть от параметров разностной схемы.

В численном решении задачи можно выделить три этапа. На первом проводится решение уравнения (5) с граничным условием (8) для определения поля давления при фиксированных распределении скорости и форме капли. На втором этапе проводится решение уравнений (3), (4) при граничных условиях (6), (7), (9) и находится поле скоростей при фиксированных давлении и форме поверхности капли. На третьем этапе из уравнений

= г* + Г_г|_г • At, ^^Z+А<|^ = ^ + ^_г- At (10)

определяется новая форма капли. В (10) г, есть поперечный радиус капли на высоте г₆ (рис. 1).

Радиус пятна смачивания определяется из условия отсутствия гистерезиса смачивания, т.е. в предположении, что краевой угол всегда один и тот же и определяется свойствами границы жидкость-газ-твердое тело. При построении новой формы капли участки между точками свободной границы ^г-*^, ^Z/^+Aj| аппроксимируются отрезками прямых. Затем производится построение новой разностной сетки с учетом изменений формы. Таким образом, использованный численный метод является одним из методов расщепления по физическим процессам [9].

Рис. 2. Основная мода колебаний. Мгновенное распределение скорости течений в капле

Обсуждение результатов

В разностной формулировке форма капли определяется радиусами своих поперечных сечений, поэтому для моделирования ее начального неравновесного состояния достаточно задать произвольные радиусы {?;•}, совместимые с безразмерным объемом капли, равным V = 4я73. В расчетах в качестве неравновесных начальных {г,} использовались равновесные значения, най денные в предварительном расчете для капли жидкости с поверхностным натяжением, немного отличающимся от исходного. Наибольшее отклонение радиуса г, от равновесного значения со ставляло менее 1 мкм.

На рис. 2 изображено поле скоростей в поперечном сечении капли воды с радиусом равнове

ликой капли, равным R = 1,0 мм. Изучение мгновенных картин распределения скоростей показы-

Дг(мкм)

0.8 -,

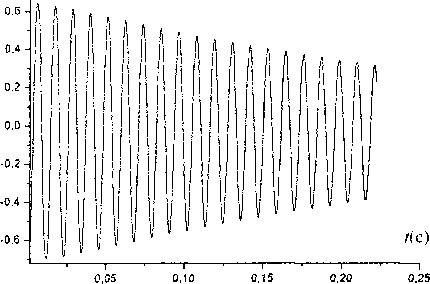
Рис. 3. Временная зависимость отклонения высоты колеблющейся капли от равновесной

данные численного эксперимента. Последняя

минимизация целевой функции - методом Розенброка [10].

вает, что в основной моде колебаний капля остается выпуклой, испытывая периодические сжатия-расширения в осевом и радиальном направлениях - подобно тому, как колеблется свободная капля в своей основной моде. На рис. 3 изображена временная зависимость отклонения высоты капли от ее равновесного значения для тех же условий, что и на рис. 2. Анализ этой зависимости показывает, что на этапе, когда колебания уже установились, но еще не слишком малы, она хорошо аппроксимируется затухающей синусоидой z = Ae~^pt sin(р и частоту со колебаний подгонкой этих параметров под проводилась методом наименьших квадратов, а

Коренченко А.Е., Илимбаева А.Ж.,                 Численное исследование свободных колебаний

Бескачко В.П. _________________________________________________________________ лежащей капли

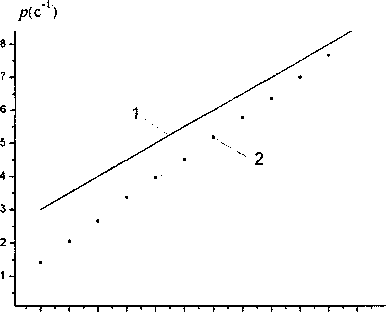
На рис. 4 и 5 изображены зависимости частоты колебаний от поверхностного натяжения и коэффициента затухания от вязкости жидкости. Результаты расчетов показаны точками. Пунктирные кривые на рисунках представляют собой результаты аппроксимации численных данных степенной функцией вида у = а^х-Ьу . Для зависимости частоты от поверхностного натяжения, ®(<т), параметр с степенной функции оказался равен 0,497, а для зависимости р(у) с = 0,989 . Это позволяет заключить, что характер этих зависимостей качественно одинаков для лежащей и свободной капли: со ~ 4о и р ~ v .

Однако абсолютные значения частот и коэффициентов затухания колебаний лежащей и свободной капель одной и той же жидкости, имеющих одинаковый размер, существенно отличаются. Сплошными линиями на рис. 4 и 5 изображены аналитические зависимости (1), (2) для колебаний свободной капли. Видно, что частоты основной моды колебаний свободной и лежащей ка-

0,6 0,7         0,9                1.2 1.3 1.4 1,5 1.6       ., и-Ю (м -с)

Рис. 5. Зависимость коэффициента затухания колебаний от вязкости жидкости: 1 - аналитическая теория [2, 3], 2 - численный расчет

юоо п

500-■

400 -I----------1----------,----------]----------,----------1----------,----------1----------,----------,---------------------1----------,----------1,

0,05     0.06     0.07     0.08     0.09     0.100.11

сг(Н/м)

Рис. 4. Зависимость частоты свободных колебаний лежащей капли от поверхностного натяжения на границе «жидкость-газ»: 1 - аналитическая теория [2, 3],

• 2 - численный расчет

пли отличаются в рассмотренном диапазоне изменения а более чем на 30 %, причем разница возрастает с увеличением коэффициента поверхностного натяжения. Различие в значениях коэффициента затухания колебаний имеет такую же относительную величину и увеличивается с уменьшением коэффициента вязкости.

Заключение

Проведен численный анализ эволюции формы лежащей капли, выведенной в начальный момент из состояния механического равновесия. Показано, что обратный переход в положение равновесия происходит в виде затухающих колебаний, параметры которых (частота и коэффициент затухания) зависят от свойств жидкости. Величины этих параметров существенно отличаются для свободной и лежащей капель, что необходимо учитывать при интерпретации опытных данных [4].

Работа выполнена при финансовой поддержке РФФИ, проект № 10-03-00719-а.