Численное исследование течений полимерных жидкостей в канале шнекового экструдера на основе одно– и двухмерных моделей

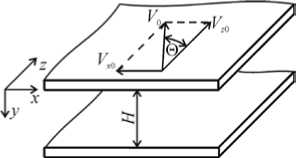
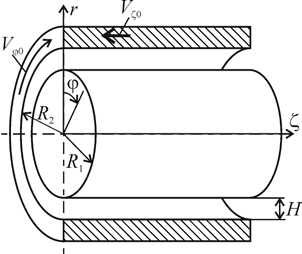
В настоящее время для описания процессов течения расплавов и растворов полимеров в винтовых каналах экструдеров широкое распространение получили одно- и двухмерные модели [1–6]. Такие модели могут быть построены в декартовой (плоские модели) или цилиндрической (осесимметричные модели) системах координат. На рисунке 1 представлены схемы различных моделей: плоская одномерная (модель 1); плоская двухмерная (модель 2); осесимметричная одномерная (модель 3); осесимметричная двухмерная (модель 4). Одномерные модели, в отличие от двухмерных, не учитывают влияние трения жидкости о боковые стенки канала на процесс течения. В плоских моделях не принимается во внимание кривизна канала. Отсюда следует, что осесимметричная двухмерная модель (модель 4, см. Рис. 1, г )

а

в

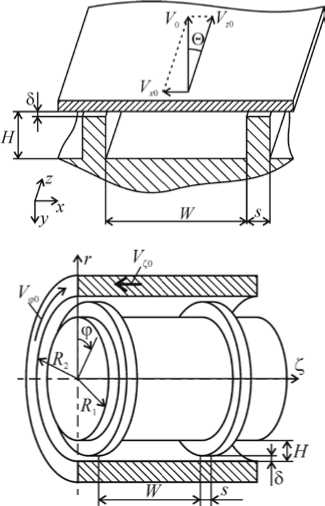
Рис. 1. Схемы моделей: модель 1 ( а ); модель 2 ( б ); модель 3 ( в ); модель 4 ( г )

наиболее полно описывает особенности течения жидкости в винтовом канале экструдера. При построении математических моделей течения жидкости в винтовых каналах экструдеров используются следующие общие допущения: рассматривается обращенное движение несжимаемой жидкости; течение считается установившимся изотермическим безынерционным; утечки через гребень винта не берутся в расчет.

В плоских моделях (Рис. 1 а , б) бесконечная верхняя пластина двигается под углом 0 со скоростью V 0 относительно продольной оси канала; проекции скорости на оси x и z определяются по формулам V x ₀ = - V ₀sin 0 и V z ₀ = V ₀cos 0 ; H — глубина канала; 5 — зазор между гребнем нарезки и внутренней поверхностью цилиндра (в данной работе величина зазора принимается равной нулю); s — ширина гребня нарезки. В осесимметричных моделях корпус вращается с окружной скоростью V _{ф 0} = V ₀cos 0 и перемещается вдоль оси £ со скоростью V _{Z 0} = - V ₀sin 0 (см. Рис. 1 в , г ). Здесь: 0 — угол подъема винтовой линии; H — глубина канала; 5 — зазор между гребнем нарезки и внутренней поверхностью цилиндра; 5 — ширина гребня нарезки; W — ширина канала; ф — окружная координата. Кривизна канала определяется параметром a = R 1 /R 2 ; изменение глубины H достигается путем изменения радиуса R ₁ при постоянном R ₂ .

В плоской одномерной модели (модель сложного сдвига) рассматривается течение жидкости между двумя бесконечными пластинами (Рис. 1, а ). Уравнения движения в этом случае имеют вид:

д Г д V , )

I цэ I дУI дy J д Г д vz )

I ц_э I д У I д y J

дР дx ’ дР дz ’

где ц_э — эффективная вязкость жидкости; v_x , v_z — проекции вектора скорости на оси x и z соответственно; д Р /д x , д Р /д z — градиенты давления в канале между пластинами, действующие в направлении координат x и z .

Реологическое уравнение степенной жидкости представляется как

,          ( n - 1)/2

Ц э = Ц о ( I 2/² )

где I ₂ — квадратичный инвариант тензора скоростей деформаций; n — показатель аномалии вязкости жидкости; ц₀ — коэффициент консистенции. Квадратичный инвариант тензора скоростей деформаций 1 ₂ в данной постановке определяется по формуле

/ х 2    / X 2

I₂    Гд v_x )   Гд v_z )

x । z

.

2 V д У J L д У J

Осесимметричная модель описывает течение в зазоре между двумя коаксиальными цилиндрами бесконечной длины (Рис. 1, в ). Уравнения движения для модели 3 записываются в виде:

д	Г Ц э	Г 5v   v ф     ф —	+ 2Цэ Г	д v ф	- v ^I	= 1 д P
д r		V д r r J д Г Гд v — цэ I — д r ^ V д r	r V П+- JJ r	д r д v ^ д r	r J _ o P = dZ	r дф ,

где vф, v? — проекции вектора скорости на оси ф и Z соответственно. Для квадратичного инварианта тензора скоростей деформаций I2 в этом случае имеет место соотношение к=[ r д[ v»)12/д!) 2. 2     д r V r J V д r J

В отличие от одномерных моделей двухмерные модели учитывают влияние на процесс течения трения жидкости о боковые стенки канала.

Движение и несжимаемость жидкости в случае плоской двухмерной модели (модель 2, Рис. 1, б ) описываются уравнениями:

5 v, —- + 5x 5 vy 5y - = 0, (8) 2 — I 5x I ।   5 vx Цэ v    5x I 5 I J + 5y V I Цэ 1 5 vx +дvL II = v 5y   5x ) ) 5P 5x ’ (9) 2-I 5y 1 ।   5 vy Цэ^" v    5y I 5 I 1 Цэ 1 5 vx +5vr II = ч 5y   5x ) ) 5P 5y ’ (10) 5 I | Цэ 5 vz I —z" I + " 2I 5 vz I  5P Цэ      I =     , (11) где vx , vy , vz — компоненты вектора скорости. В такой постановке второй инвариант имеет вид:

I ² = 2

I 5 ^v I I "T" I

I 5 x )

V

+    +

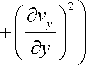
5 y

5 x

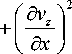
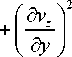
Осесимметричной двухмерной постановке (модель 4, Рис. 1, г ) отвечают уравнения движения и несжимаемости вида:

5 U  5 v_r

—I 2ц_э-- 5 r V 5 r

^{1 ( v} + ^v = 0

r 5 r    5z

2ц_э 5 v r r 5 r

2        5

--7 Ц, v, +-- 2 Э ^r r         5 x

1^{5 v} z 5 v, ц_э —- + —-

^Э V 5 r 5£

5 P

5 r ’

д     (dv   v           f 8v v fl ( dv 1 flP ф     ф     , Цэ ф     ф , '           ф _ 1

^Ц э I—I ⁺1—I +—I ^Ц э I= , 5 r    V 5 r   r ) r V 5 r   r ) 5 r V    5Z )   r 5ф

5 r

5vz   5v„ I   цэ 15vz   5v„ I   5 I _   5vz I5

1| +11| +1 2цэ| =

5r   5Z )j   r V 5r   5Z)  5Z V    5Z)5Z

где v_r , v _ф , v _? — компоненты вектора скорости. Второй инвариант в этом случае записывается как:

I ² = 2

+

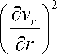
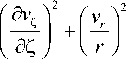
Я ( v ф ^r ^I —

5 r V r

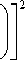
1 ^{5 v} ^ 5 v_r I   1^{5 v} ф I

+ I + I +I I

V 5 r    5Z ) V 5Z )

Продольные компоненты скорости находятся из решения дифференциальных уравнений движения (2), (6), (11), (16) для режима заданного расхода или режима заданного градиента давления. При режиме заданного расхода уравнения движения дополняются выражениями, описывающими расход жидкости через поперечное сечение канала: – в одномерных моделях

HR

Qz = Qо = WJ vzdy ;  Qф= Q, = W J vфrdr,(18)

а поперечные компоненты скорости определяются из условия равенства расхода нулю

H

R 2

J v _z rdr = 0 ;

R 1

J ^vx dy = 0;

– в двухмерных моделях

WH                     W R 2

Q = Q o = JJ vzdydx ; Q , = Q о = Jf v _Ф rdrd - .                          ⁽²⁰⁾

00                          0 R ₁

На границах области скорость жидкости задается исходя из условий прилипания к непроницаемым твердым стенкам.

Реализация каждой из рассматриваемых моделей, описываемых соответствующими уравнениями из (1–20), осуществляется с помощью метода конечных элементов. Для двухмерных моделей компоненты скорости аппроксимируются квадратичным, а давление — линейным полиномами на треугольном элементе. В одномерных моделях используются линейные симплекс-элементы.

Для ньютоновской жидкости решение получается за один шаг, для неньютоновской задача решается итерационно. На первом шаге задается некоторое распределение вязкости и расход. При известном, сохраняющем постоянство на протяжении всего итерационного процесса значении расхода определяются поля скоростей и градиенты давления, после чего пересчитывается распределение вязкости в сечении канала. Второй и все последующие шаги вычислений аналогичны первому шагу. Итерационный процесс продолжается до тех пор, пока максимальная невязка по скорости между текущей и предыдущей итерациями не станет меньше наперед заданной малой величины. Для ньютоновской жидкости сходимость решения проверяется путем сравнения с существующими точными аналитическими решениями [2], для неньютоновской жидкости — путем сгущения сетки и оценкой по чебышевской и энергетической нормам.

Для возможности сравнения градиентов давления в плоской и осесимметричной моделях принимается, что градиент давления дР/ дф действует по окружности радиуса R ₀ = ( R 1 + R ₂ ) /2 [7], тогда величина

Ос дР 1 дР градиента давления в осесимметричном случае определяется по формуле: — =--.

д z     R 0 дф

Поскольку двухмерная осесимметричная модель (модель 4, Рис. 1, г ) наиболее полно реализует особенности течения жидкости в винтовом канале экструдера, количественное сравнение моделей 1–3 проведено именно с ней в режиме заданного расхода. Исходные данные для расчетов содержит таблица 1.

На первом этапе исследованы ньютоновские жидкости с вязкостью ц = 15260 Па - с (показатель аномалии n = 1).

Таблица 1. Исходные данные

Внутренний радиус цилиндра (корпуса) R 2 , мм	31,75	Частота вращения шнека N , об/мин	40
Наружный радиус шнека R 2 , мм	31,75	Окружная скорость V 0 , м/с	0,133
Шаг винтовой нарезки, мм	63,5	Проекция окружной скорости Vz 0 = V ,0 , м/с	0,127
Ширина канала W , мм	54,0	Проекция окружной скорости Vx 0 = V .0 , м/с	–0,04
Угол подъема винтовой линии 0	17 0 39 ,	Плотность материала р , кг/м3	810

Результирующий расход жидкости в канале, независимо от модели, складывается из вынужденной и напорной составляющих расхода. Так, для модели 4

Q Ос2 Ос2 Ос2

Рз = QВн + QНп , где QВОнс2 , QНОпс2 — вынужденная и напорная составляющие объемного результирующего расхода QРОзс2 , рассчитанные по осесимметричной двухмерной модели. Сопоставление различных моделей можно осуществить по расходу с помощью поправочных коэффициентов, которые используются Тадмором [2] при сравнении плоской одномерной и плоской двухмерной моделей. Подобные коэффициенты применяются в работе [8] для оценки влияния кривизны канала при исследовании течения ньютоновской жидкости в винтовом канале экструдера в рамках одномерной постановки.

Выражение для производительности (21) можно записать через вынужденную и напорную составляющие расхода, полученные по осесимметричной одномерной модели (модель 3, Рис. 1, в )

QО:² = Q Онс ² + Q.. = Q Онс ¹ F b*h + Q h⁰:¹ f; ,                                  (22)

где FВ*н , FН*п — коэффициенты формы канала, учитывающие влияние боковых стенок при сдвиговом и напорном течениях, соответственно, в осесимметричных случаях.

Аналогично выглядит выражение связи объемного результирующего расхода в плоской двухмерной модели Q Пл ² (модель 2, Рис. 1, б) с вынужденной ( Q ^” ¹) и напорной ( Q Нл ¹) составляющими расхода в одномерной модели (модель 1, Рис. 1, а ):

Пл2 Пл2 Пл2 Пл1         Пл1

QРз = QВн + QHп = QBн F Вн + QНп FHп , где FBн, FHп — коэффициенты формы канала для плоских моделей, учитывающие влияние боковых стенок в случае сдвигового и напорного течений.

На рисунке 2 показано изменение коэффициентов формы для каналов с различной геометрией и кривизной, характеризуемых геометрическим параметром a = R 1/ R ₂ . Из рисунка видно достаточно хорошее совпадение одноименных кривых F B_н , F H _п (полученных с учетом влияния стенок) и F _Bн, F _Hп для указанного диапазона изменения геометрического параметра a , что свидетельствует о совпадении результатов для двухмерной плоской и двухмерной осесимметричной моделей.

При отношении HW , стремящемся к нулю, разница между одномерными и двухмерными моделями течения ньютоновской жидкости практически исчезает. Вместе с тем, отличие напорно-расходных характеристик в случае использования одно- и двухмерных моделей при достижении H/W значения 0,2 будет превышать 10%, при 0,4 — больше 20% и так далее. В пластицирующих экструдерах величина HW , как правило, меньше 0,2. Однако в зоне плавления отношение ширины канала, которую занимает расплав полимера, к высоте может значительно превышать 0,2 , что необходимо учитывать при построении математических моделей пластицирующей экструзии и ряда шнековых насосов и отдавать предпочтение двухмерным моделям.

Результирующий расход для модели 4 можно записать через соответствующие расходы плоской двухмерной модели (модель 2, Рис. 1, б )

_{Q Р} О _з с2

Ос2 Ос2

Q Вн + ^Q Hп

Пл2 * Пл2 *

^Q Bн f Вн + Q Нп f Нп ,

где / _В * _н, / Н _п — коэффициенты формы, учитывающие кривизну канала, для сдвигового и напорного течений соответственно.

Аналогичное выражение для результирующего расхода осесимметричной одномерной модели имеет вид:

Ос1 Ос1 Ос1 Пл1          Пл1

QРз    QВн + QНп   QВн f Вн + QНп f Нп , где /Вн, /Нп — коэффициенты формы, учитывающие кривизну канала, для сдвигового и напорного течений.

На рисунке 3 пунктирными линиями показаны зависимости коэффициентов формы / _Вн и / _Нп, которые обусловливаются только геометрическим параметром a , характеризующим степень кривизны канала. Из рисунка видно, что для рассматриваемого диапазона изменения геометрического параметра наибольший вклад в расхождение результирующих расходов между плоской и осесимметричной одномерными моделями вносит коэффициент формы для сдвигового течения / _Вн. При этом / _Вн >  1,

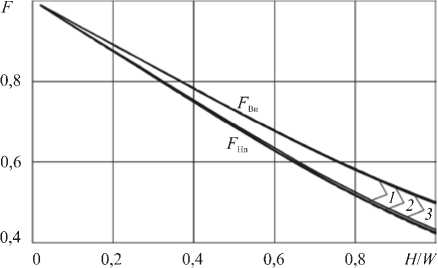
Рис. 2. Коэффициенты формы для сдвигового и напорного течений при различных значениях параметра геометрии a : 0,9 (кривая 1 ); 0,7 ( 2 ); 0,5 ( 3 ); F_B н , F н _п   ;

Рис. 3. Коэффициенты формы для сдвигового и напорного течений при различных значениях отношения H]W : ^0,05 (кривая 1 ); ^{0,1 (} 2 ); ^{0,4 (} 3 ); / „ , / н_п - ;

F *   F*

Вн , Нп

*        .

f Вн , f Нп

a f Нп <  1. Коэффициенты формы f *, и / Нп в уравнении (23) (кривые 1 - 3 на рисунке 3) определяются не только параметром a , но и зависят от отношения HW , влияние которого, как свидетельствует рисунок, мало для рассматриваемого диапазона изменения HW .

Для того чтобы вычислить производительность экструдера в рамках двухмерной осесимметричной модели (модель 4) по результатам, полученным на основе плоской одномерной модели (модель 1), необходимо использовать поправочные коэффициенты, учитывающие трение жидкости о боковые стенки канала и кривизну канала. Такой переход можно осуществить по формулам (22), (24):

Ос2 Ос1 * Ос1 *       Пл1 *           Пл1 *            Пл1          Пл1

QP3    QВн ЕВн + QНп ЕНп  QВн ЕВн fВн + QНп ЕНп fНп  QВн kВн + QНп kНп , где кВн = ЕВнfВн, кНп = ЕНп fНп — результирующие коэффициенты формы. Зависимости коэффициентов формы kВн и kНп от величин HW и a определяются комбинацией коэффициентов FВ*н , FН*п , fВн , fНп , являющихся функциями указанных параметров (см. Рис. 2 и 3).

На втором этапе сравнение моделей проводится для псевдопластических жидкостей при тех же геометрических и технологических параметрах экструдера, что и для ньютоновских жидкостей (см. Табл. 1). Коэффициент консистенции ц ₀, характеризующий вязкость жидкости, в реологическом уравнении (3) равняется 15260 Па - с n . Другие параметры, использованные в расчетах, содержит таблица 2.

Таблица 2. Значения варьируемых параметров

№ варианта	a = R1 /R 2	H , мм	HW	n	№ варианта	a = R , / R 2	H , мм	HW	n
1	0,9	3,175	0,059	1,0	4	0,7	9,525	0,176	1,0
2				0,7	5				0,7
3				0,4	6				0,4

На рисунке 4 представлены напорно-расходные кривые, построенные по результатам, полученным на основе конечно-элементных одномерных и двухмерных плоских и осесимметричных моделей для некоторых вариантов параметров из таблицы 2. Диапазон изменения объемного расхода определяется безразмерной величиной B = QIq BH' , лежащей в диапазонное от 0 до 1,1, что соответствует изменению размерного расхода при H = 3,175 мм от 0 до 1,2 - 10 ^{- 5} м³/с и при H = 9,525мм — от 0 до 3,6 - 10 ^{- 5} м³/с. По оси ординат откладывается значение перепада давления в канале длиной 1 м, что численно соответствует значению градиента давления. Из рисунков видно, что при увеличении кривизны канала

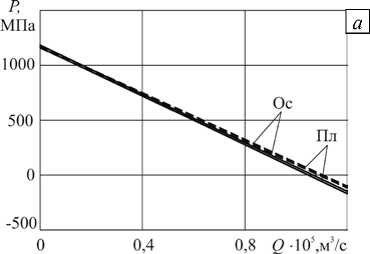
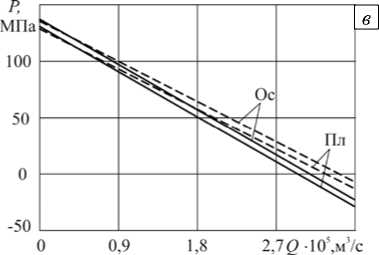
Рис. 4. Напорно-расходные кривые при 1-м ( а ), 3-м ( б ), 4-м ( в ) одномерных ( ) и двухмерных ( ) плоских (Пл) и модель 2 (Пл) – ; модель 3 (Ос) – ; модель 4 (Ос) –

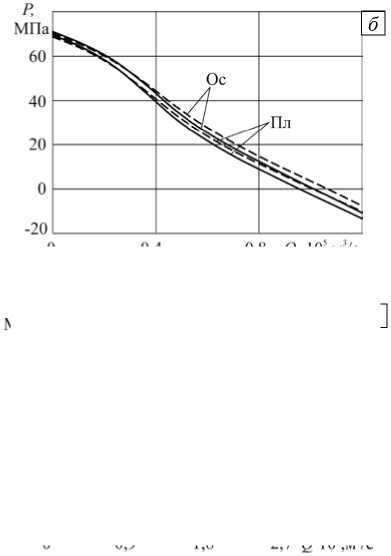
и 6-м ( г ) вариантах параметров из таблицы 2 для разных типов осесимметричных (Ос) моделей;( модель 1 (Пл) –        ;

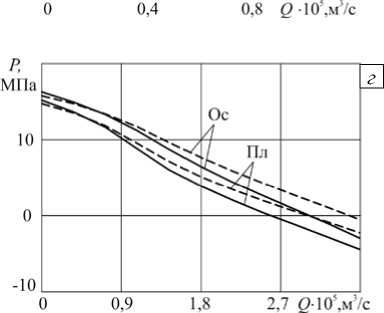
(уменьшении геометрического параметра a ) возрастает различие между напорно-расходными характеристиками, полученными в соответствии с плоской и осесимметричной моделями. Кроме того, расхождение растет при увеличении показателя аномалии вязкости жидкости. Изменение геометрии канала существенно влияет на номинальное значение градиента давления.

При решении задач с напорным течением наибольшая погрешность в вычислениях возникает при расчете градиентов давления. Для определения относительного расхождения 5 между градиентами (перепадами) давления в зависимости от безразмерного расхода B , найдем невязку градиента давления между рассматриваемыми моделями при вариантах параметров, представленных в таблице 2, как

5 ^Пл 2

5 ^Ос|

5 ^Пл 1

dP Пл2	dP Ос2 )	dP	Ос2	■ 100%,
	—	/ —
dz	dz J	dz	Q Озс2 = 0
dP Ос1	dP Ос2 )	dP	Ос2	100%,
	—	/ —
dz	dz   J у	dz	Q рОзс2 = 0
dP Пл1	dP Ос2 )	dP	Ос2	100% .
	—	/ —
dz	dz   J/	dz	Q Р°" = 0

Пл1        Пл2        Ос1        Ос2

d p    a p    a p    a p                                  „

Здесь:      ,       ,      ,        — градиенты давления для плоской и осесимметричной одно- дz      дz      дz     дz и двухмерных моделей;

dP

Ос2

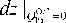
градиент давления для осесимметричной двухмерной модели

при результирующем расходе Q _Р^О_з^с2 равном нулю.

На рисунке 5 показано изменение 5 в зависимости от безразмерного расхода B при различных значениях геометрического параметра a , а также от геометрического параметра а при B = 1 и различных значениях показателя аномалии вязкости n . Кривые невязки по давлению 5 ^Пл 2 для двухмерных моделей изображены сплошной линией. Из рисунка 5, а , б видно, что все они расположены в области отрицательных значений, и уменьшение геометрического параметра a (увеличение кривизны канала) приводит к росту расхождения между напорно-расходными кривыми, построенными по моделям 2 и 4. Это справедливо для ньютоновских и псевдопластических жидкостей.

Наличие аномалии вязкости существенно увеличивает различие между результатами, полученными по плоским и осесимметричным моделям. Например, при а = 0,7 (см. Рис. 5, б) для ньютоновской жидкости

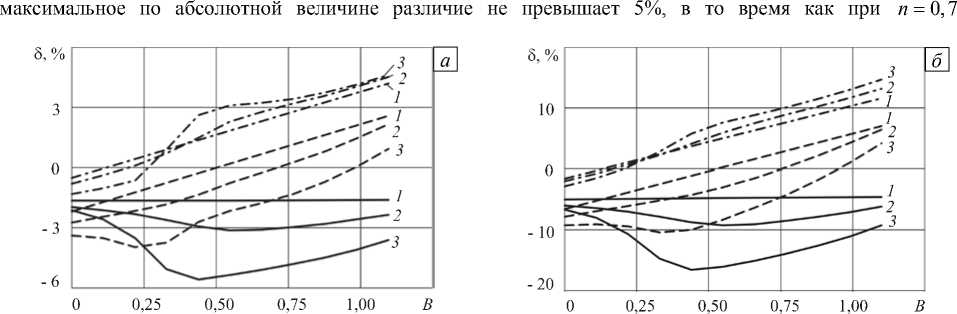
Рис. 5. Относительные расхождения градиентов давления в зависимости от безразмерного расхода при а = 0,9 ( HW = 0,059 ) ( а ) и а = 0,7 ( HW = 0,176 ) ( б ), а также от геометрического параметра а при B = 1 ( в ) при различных значениях показателя аномалии вязкости n = 1,0 (кривые 1 );

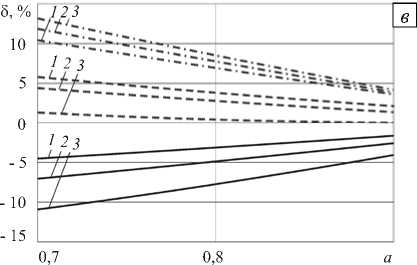
n = 0,7 ( 2 ); n = 0,4 ( 3 ): 5 ^Пл2 - ------; 5 ^Ос|

;

Пл1

5  — расхождение достигает 11%, а при n = 0,4 — 18%. Таким образом, для аномально-вязкой жидкости с показателем аномалии n = 0,4 различие между моделями увеличивается по отношению к ньютоновской жидкости более чем в 3 раза. Кроме того, из рисунка 5 видно, что для аномально-вязких жидкостей значение 5Пл2 зависит от величины заданного расхода.

Значительно сильнее связаны с изменением расхода различия между напорно-расходными характеристиками моделей 1, 3 и модели 4. При уменьшении параметра a растет отношение HW (см. Табл. 2), что заметно сказывается на различии между напорно-расходными кривыми этих моделей. Увеличение показателя аномалии вязкости больше влияет на кривые 5 ^Пл1, чем на 5 ^Ос1. Расхождение расходно-напорных кривых моделей 3 и 4 обуславливается тем, что осесимметричная одномерная модель не учитывает влияние боковых стенок канала на процесс течения жидкости. Из рисунка 5 видно, что при B >  0,25 кривые 5 ^Ос1 лежат в области положительных значений, что обуславливается тормозящим действием боковых стенок.

В модели 1, по отношению к модели 4, не учитывается влияние боковых стенок и кривизны. Поскольку при B >  0,25 действие этих факторов противоположно по знаку, то при определенных значениях безразмерного расхода градиенты давлений 5 ^Пл1 могут компенсировать друга друга. Например, (см. Рис. 5) 5 ^Пл1 ^ 0 при n = 1 и B « 0,5 (пунктирная линия 1 ), при n = 0,7 и B « 0,75 (пунктирная линия 2 ), при n = 0,4 и B ® 1 (пунктирная линия 3 ). Этот факт нашел экспериментальное подтверждение в шнековых насосах, процесс течения жидкости в которых плоская одномерная модель сложного сдвига описывала адекватнее, чем плоская двухмерная модель [9].

В результате исследования процесса течения жидкости в сужающемся канале с помощью различных моделей получены практически те же закономерности, что и для канала постоянной глубины (Рис. 6). На рисунке показаны профили скоростей в трех сечениях по длине канала (длина канала составляла 2 м), построенные по одномерной осесимметричной модели при B = 1,5 . Пунктирной линией показаны профили скоростей для ньютоновской жидкости, сплошной — для аномально-вязкой жидкости с n = 0, 4 . Из рисунка по направлению изгиба кривых видно, что при заданном расходе в первых двух сечениях градиент давления имеет положительный знак, а в третьем сечении — отрицательный.

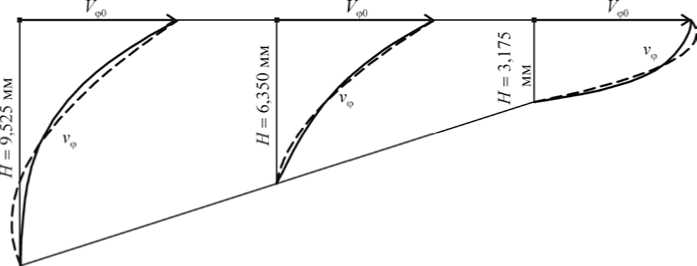
Рис. 6. Профили окружной скорости v _ф : n = 1,0 -     ; n = 0,4 -

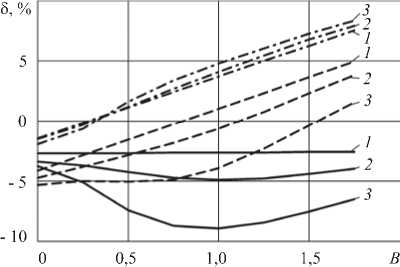
Рис. 7. Относительные расхождения градиентов давления 5 в зависимости от безразмерного расхода: 5 ^Пл2 -----;

5 ^Ос1  ---; 5 ^П л1  --- ; n = 1,0 (кривая 1 ); n = 0,7 ( 2 );

n = 0,4 ( 3 )

Относительные расхождения 5 между напорнорасходными кривыми, построенными по плоским и осесимметричным моделям, демонстрирует рисунок 7. Кривые аналогичны соответствующим зависимостям, представленным на рисунке 5, для каналов с постоянной высотой и занимают промежуточные положения по отношению к соответствующим кривым, приведенным на рисунке 5, а , б .

Подводя итог вышесказанному, можно отметить, что одномерные модели достаточно неплохо проявляют себя в задачах, где температура по сечению канала распределена достаточно равномерно, хотя может изменяться по длине канала (что соответствует изотермической постановке рассмотренных задач). Подобная ситуация характерна для шнековых насосов, винтовых уплотнений [10]. При этом если необходимо выбирать между плоской и осесимметричной одномерными моделями, то предпочтение следует отдавать плоской модели, поскольку она зачастую с большей точностью позволяет получать расходно-напорные характеристики, что, как уже отмечалось, имеет экспериментальное подтверждение при моделировании работы шнековых насосов [9]. Недостаток одномерных моделей по отношению к двухмерным состоит в том, что они не позволяют описать циркуляцию жидкости в поперечном сечении канала.

В пластицирующих экструдерах, где происходит плавление полимеров, в поперечном сечении канала могут иметь место значительные градиенты температуры, а конвективный перенос тепла в расплаве полимера преобладает над диффузионным. Кроме того, в зоне плавления ширина бассейна с расплавом может быть соизмерима с высотой канала. Использование одномерных моделей в этом случае менее целесообразно.

Осесимметричные двухмерные модели, в отличие от плоских, более точны, поскольку позволяют учитывать кривизну канала. Вместе с тем в канале пластицирующего экструдера в расплавленном состоянии материал находится в зонах плавления и дозирования, где канал имеет сужающуюся форму, а значения геометрического параметра a максимальны. При этом различие между напорно-расходными характеристиками, полученными по плоской и осесимметричной двухмерным моделям, минимально. Поэтому применение плоской двухмерной модели для описания процессов течения в каналах пластицирующих экструдеров является достаточно обоснованным.