Численное исследование термомеханического поведения и эволюции микроструктуры заготовки из никелевого сплава в процессе ее осадки

Жаропрочные сплавы системы «Ni–Cr–Fe», разработанные в конце 30-х годов XX века, успешно используются в аэрокосмической промышленности. Такие сплавы способны длительное время работать при интенсивных статических и динамических нагрузках в условиях высоких температур и сохранять стабильные механические свойства. Так, например, рабочая температура современных жаропрочных сплавов на основе никеля достигает ~1100°С. Одним из наиболее распространенных серийных никелевых сплавов является Waspaloy, который находит широкое применение для изготовления некоторых элементов авиационных газотурбинных двигателей (рабочих и сопловых лопаток, дисков ротора турбины и другого) с максимальной температурой эксплуатации ~870°С.

Статья содержит результаты продолжения исследований, представленных в работе [1], где рассмотрено влияние скорости деформирования на эволюцию микроструктуры при горячей пластической осадке никелевого сплава Waspaloy. Микроструктура материала характеризовалась средним размером зерна и объемной долей рекристаллизованной части зерен. Для определения влияния параметров процесса на формирование структуры сплава Waspaloy выполнен расчет теплового и деформированного состояний массивного слитка в процессе свободной осадки при скоростях перемещения верхнего бойка 50 и 100 мм/c. Изменение микроструктуры (формирование малодефектных зародышей новых зерен и их последующий рост), происходящее в результате пластической деформации, — процесс, известный под названием динамическая рекристаллизация [2]. Для описания кинетики этого процесса в работе [1] использовалась модель Джонсона–Мела–Аврами–Колмогорова. Выявлено, что при скорости перемещения верхнего бойка 100 мм/c возникает более мелкозернистая структура, чем при скорости 50 мм/c. В первом случае средний размер зерна в области наиболее интенсивной деформации составил 13,9 мкм, тогда как во втором — 14,4 мкм, при среднем начальном размере зерна ~25 мкм. В работе [1] также показано, что при более высокой скорости осадки (100 мм/с) процесс динамической рекристаллизации протекает более интенсивно и в него вовлекается больший объем материала.

В реальном технологическом процессе заготовка сначала нагревается в печи до температуры, обеспечивающей наилучшую пластичность при обработке давлением, а затем переносится на оборудование, которое осуществляет осадку до определяемого технологией диаметра. При переносе заготовка охлаждается, в ней устанавливается неоднородное, начальное для последующего процесса осадки распределение температуры, что влияет на динамическую рекристаллизацию, которая существенно зависит от деформации и температуры. Поэтому имеет смысл анализировать эволюцию микроструктуры с учетом охлаждения массивного слитка на воздухе во время его транспортировки к деформирующему оборудованию.

В настоящей работе проводится исследование влияния начального распределения температуры, образующегося в результате охлаждения слитка на воздухе при его переносе от печи до деформирующего оборудования, на изменения, происходящие в микроструктуре сплава Waspaloy. На основании ранее проведенных исследований, изложенных в работе [1], скорость перемещения верхнего бойка принимается равной 100 мм/с.

Известно, что механические свойства металлов и сплавов (такие как прочность, пластичность, ударная вязкость и другие) зависят от структуры поликристаллических заготовок [2–4]. Наиболее важным структурным параметром является размер зерна. В результате уменьшения (измельчения) зерна в процессе горячей обработки давлением повышаются прочностные и пластические свойства металлов [5]. К таким процессам относятся ковка, штамповка, прессование, волочение и другие [6, 7]. Осадка заготовки с хвостовиком — это основная операция свободной ковки, которая применяется в качестве заготовительной перед процессом протяжки (обжатия) для улучшения качества и структуры металла. Именно эта операция изучается в настоящей статье. Последующая протяжка заготовки здесь не рассматривается.

Технологический процесс горячей обработки давлением крупного слитка до получения заданных геометрических размеров при определенном температурно-скоростном воздействии включает в себя охлаждение слитка на воздухе в течение 45 с при транспортировке его от печи до деформирующего оборудования и операцию свободной осадки. Цель моделирования — изучение изменений, которые происходят в микроструктуре материала в процессе горячей пластической деформации. В качестве материала для исследования эволюции зеренной структуры, как и в работе [1], выбран металлический сплав Waspaloy, микроструктура которого описывается с помощью набора параметров.

Компьютерное моделирование осуществляется на базе программного комплекса Deform-2D/3D [8, 9]. Комплекс основан на методе конечных элементов и позволяет анализировать формоизменение заготовки в различных процессах обработки давлением, рассчитывать напряженно-деформированное и тепловое состояния во всем объеме заготовки в процессе ковки с учетом геометрической и физической нелинейностей.

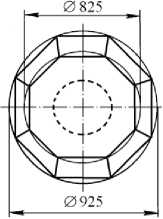
Объектом исследования является массивный слиток весом 9300 кг, который показан на рисунке 1. Слиток состоит из тела и хвостовика (цапфы). В первоначальном состоянии тело заготовки имеет вид усеченной восьмигранной пирамиды с площадями оснований: нижнего ~6050,18 см2 и верхнего ~4812,75 см2. Цапфа представляет собой цилиндр высотой 500 мм и диаметром 300 мм.

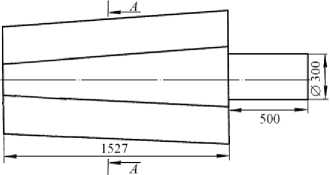
Рис. 1. Слиток с исходными геометрическими размерами, мм: вид спереди ( а ), вид слева ( б ); поперечное сечение А – А проходит через середину тела слитка и перпендикулярно его центральной оси

Трехмерная модель слитка, выполненная в программе SolidWorks, приведена на рисунке 2 а . Пример дискретизации расчетной области тетраэдральными конечными элементами показан на рисунке 2 б . Дискретный аналог исследуемого трехмерного тела содержит 52168 конечных элементов (оптимальное количество элементов, полученное в результате численных экспериментов) и 11298 узловых неизвестных. При построении сетки учитывается сложность геометрии объекта исследования, на его границе плотность сетки увеличена. При обработке давлением подвергается деформации только тело слитка, форма хвостовика (цапфы), который служит для удержания заготовки в процессе осадки, остается неизменной. Однако отказаться от учета хвостовика при моделировании нельзя, так как он влияет на скорость остывания нижнего торца слитка. Вследствие этого конечно-элементная сетка в этой области делается менее плотной.

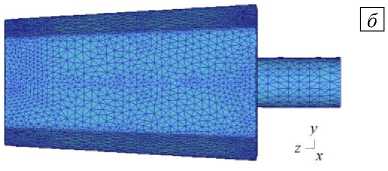
Рис. 2. Объемная модель слитка ( а ), построенная в программе SolidWorks, и его конечно-элементная дискретизация ( б )

2. Охлаждение массивного слитка на воздухе при его переносе до деформирующего оборудования

Массивный слиток подвергается обработке давлением по следующей технологической схеме. Перед началом деформирования — процессом свободной осадки — слиток нагревается и выдерживается в пламенной печи до достижения однородной по всему объему температуры, равной 1000°С. Сам процесс нагрева в печи здесь не моделируется. Затем в течение 45 с слиток транспортируется по воздуху от печи до деформирующего оборудования, что приводит к его охлаждению. Полученное распределение температуры является начальным для дальнейшей операции свободной осадки.

Уравнение нестационарной теплопроводности, позволяющее вычислить температурное поле в объеме заготовки и на ее поверхности, имеет вид [10, 11]:

ST

pc— = V.(kVT) + Q .

Здесь: p — плотность вещества в текущем состоянии, кг/м³; c — удельная теплоемкость, Дж/(кг^К); T — температура по абсолютной шкале, К; V — оператор Гамильтона для текущей конфигурации; к — коэффициент теплопроводности, Вт/(м·К); Q — мощность внутренних источников тепловыделения (теплопоглощения), Вт/м³; t — текущее время, c.

Для уравнения нестационарной теплопроводности (1) необходимо задать начальное условие в виде распределения температуры внутри тела и на его поверхности S в начальный момент времени, а также граничные условия. Так, на поверхности S = S_T и S_q они имеют следующий вид:

на части ST    T = T*, на части S    -N • к V T = qN ,

где T ^* — заданное значение абсолютной температуры, N — внешняя единичная нормаль к поверхности тела в текущем состоянии, q_N = а ( T - T ) — нормальная к поверхности тела составляющая теплового потока через границу, при этом T — температура окружающей среды по абсолютной шкале, а_Е — коэффициент теплоотдачи, который рассчитывается, как

ау = а +а„.

^   sr

В последнем выражении as — коэффициент теплоотдачи конвекцией, Вт/(м2^К), а аг — коэффициент теплоотдачи излучением, который вычисляется по формуле

^а r

^эфф ( T 4 - T ⁴ )

T - T c

где ст₀ = 5,67 - 10 ⁸ Вт/(м²^К4) — постоянная Стефана-Больцмана, е эф — эффективная степень черноты материала (для сплава Waspaloy в базе комплекса Deform-2D/3D эта величина равна 0,7).

В качестве граничных условий на боковой и торцевых поверхностях рассматриваемого тела задаются условия радиационно–конвективного теплообмена в упрощенном виде, то есть они сводятся к конвективному теплообмену. Вклад лучистого теплообмена учитывается по приведенной выше формуле для коэффициента теплоотдачи излучением. При транспортировке массивного слитка от печи до инструментов, осуществляющих процесс осадки, температура окружающей среды считается равной 20°С. В этом случае коэффициент конвективной теплоотдачи a_s равняется 20 Вт/(м -К) [14].

В качестве начального условия принимается постоянное распределение температуры в слитке, равное 1000°С. В работе фигурируют шкалы Кельвина и Цельсия. Связь между шкалами определяется известным соотношением, в котором абсолютная температура получается путем прибавления величины 273,15 к температуре в градусах Цельсия.

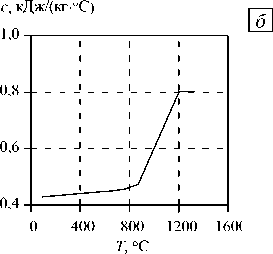
Зависящие от температуры теплофизические свойства никелевого сплава Waspaloy позаимствованы из библиотеки используемого программного комплекса Deform-2D/3D. Кривые изменения коэффициента теплопроводности и удельной теплоемкости приведены на рисунке 3.

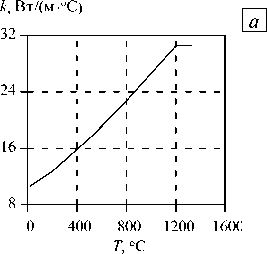
Рис. 3. Зависимости от температуры коэффициентов теплопроводности ( а ) и удельной теплоемкости ( б )

Уравнению теплопроводности (1) и граничным условиям (2) соответствует вариационное уравнение:

J[(cpT -Q)ST + kVT-V(ST)]dV + JqN STdS = 0 .

VS q

Оно получается путем применения процедуры Галеркина к уравнению (1) и граничному условию (2) 2 , представленным в однородной форме, с учетом, что области V и S не пересекаются:

J[ cp T -V-( k V T)-Q ]S TdV + J( N - k V T + qN )S TdS = 0.

VS q

Если выбирается функция T , удовлетворяющая на части S_T граничному условию (2) ! , то есть T = T * , то на S_T вариация S T = 0, и тогда второй интеграл в (4) может быть вычислен уже не по части S, а по всей поверхности S , ограничивающей объем V . В этом случае к первому слагаемому во втором интеграле применима теорема Остроградского–Гаусса:

J N - k V T S TdS = J v- ( k V T S T ) dV . SV

При использовании далее соотношения V- ( a b ) = (Va) - b + a ( V - b ), где a — любой скаляр, b — любой вектор, легко представить интеграл в правой части в виде (в предположении, что a = S T , b = k V T ):

J V-( k V T ST) dV = JsT [V-( k V T)] dV + J k V T -V(S T) dV,

VV  V откуда и следует вариационное уравнение (3). В этом уравнении объем и поверхность относятся к текущему состоянию и до решения задачи являются неопределенными величинами. Но они легко приводятся к известным объему и поверхности начального состояния. С учетом того, что элементарная масса не меняется: dm = pdV = p0dV, где p0, dV — плотность материала и элементарный объем в начальном состоянии, а также выражения, связывающего элементарные объемы в текущей и начальной конфигурациях: dV = JdV и элементарные поверхности в этих конфигурациях: dS = J4n • C-1 • n dS0, где J есть третий инвариант градиента места F, C = FT • F — мера деформации Коши-Грина, n — вектор внешней единичной нормали к поверхности в начальной конфигурации, вариационное уравнение (3) приводится к следующему конструктивному виду:

J [ ( c р₀ T - JQ ) 8 T + Jk V T -V ( 5 T ) ] dV + J J4 n • C ^{- 1} • n q_N 5 TdS_q о = 0.                (5)

V 0                                                                            S_q 0

Входящий сюда оператор Гамильтона текущего состояния V можно преобразовать в оператор Гамильтона 00

начального состояния V , если воспользоваться зависимостью: V = F ^{- T} •V . В программном комплексе Deform-2D/3D уравнение (5) реализуется методом конечных элементов.

Охлаждение крупного слитка на воздухе при транспортировке до деформирующего оборудования не сопровождается никаким внутренним производством или стоком тепла, поэтому в (5) Q = 0. В этом процессе текущая конфигурация совпадает с начальной, откуда следует, что J = 1, F = C = g , где g — единичный тензор, и уравнение (5) значительно упрощается. Полученные с его помощью результаты, демонстрирующие изменение температуры в слитке, представлены на рисунке 4.

у, мм

а

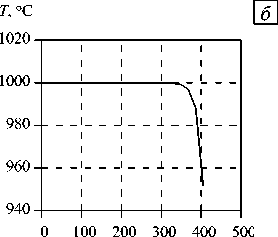
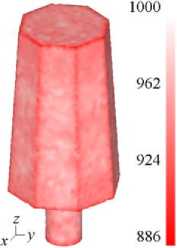
Рис. 4. Распределение температуры T ,°С на поверхности слитка в после охлаждения на воздухе в течение 45 с при его транспортировке до оборудования ( а ); график изменения температуры в зависимости от расстояния до центра слитка в сечении А – А (см. Рис. 1 б )

Температура боковой поверхности массивного слитка меняется примерно на 47°С в «узкой» приповерхностной области (см. Рис. 4 б ). Снижение температуры слитка наблюдается не более чем на ~91 мм, в глубине слитка температура не меняется. При этом присутствуют области с минимальными значениями температуры ~915°С, которые находятся на ребрах заготовки и в нижней части цапфы. Средние значения температуры на верхнем и нижнем торцах слитка, а также на поверхности цапфы составляют примерно ~943–958°С. Рассчитанное распределение температуры используется в дальнейшем как начальное при анализе деформированного состояния, возникающего при осадке заготовки на втором этапе технологического процесса.

3.    Свободная осадка массивного слитка с хвостовиком

Далее по технологии осуществляется осаживание слитка плоскопараллельными плитами — подвижной верхней и неподвижной нижней, имеющей отверстие для хвостовика диаметром 300 мм. Верхняя плита при движении вниз, вдоль вертикальной оси z , со скоростью 100 мм/c перемещается на величину u_z = 496 мм и деформирует образец. Для предотвращения существенного охлаждения слитка при контакте с деформирующими плитами производится их подогрев до температуры 400°С. Так как в реальном технологическом процессе бойки деформируются незначительно, в модели они считаются абсолютно жесткими. Для описания трения, возникающего между рабочими плитами и слитком в процессе горячей обработки давлением, используется закон Зибеля, в котором усилие трения определяется как произведение коэффициента трения на величину касательного напряжения. Жаропрочный сплав Waspaloy на никелевой основе относится к трудно обрабатываемому давлением материалу, поэтому деформирование рассматриваемого сплава производится с применением смазки, которая позволяет уменьшить действие сил трения на контактной поверхности и снизить усилие деформирования. Коэффициент трения ц принимается постоянным и равным 0,3. При указанном коэффициенте трения требуемый по технологии средний диаметр заготовки ~1060 мм достигается при средней осевой степени деформации ~32,5%. Значение последней вычисляется по формуле:

ба = (l0 - к )-100%/l0 = Al-100%/l0, где l0 — начальная высота слитка; lv — высота слитка после завершения процесса осадки, Al = l0 - lx — величина осадки.

Процесс свободной осадки слитка является медленно протекающим процессом, поэтому инерционные силы, действующие на заготовку, здесь не учитываются. В практике теоретических расчетов обработки металлов давлением в большинстве случаев также принимаются допущения о незначительном влиянии массовых сил на течение сплава [15] и пренебрежимо малых упругих деформациях, рассматриваются только пластические. Тогда математическая постановка задачи определения напряженно-деформированного состояния заготовки в процессе пластического формоизменения включает в себя [1, 12, 13]:

• -    уравнение равновесия V- T = 0;

• -    кинематическое уравнение для деформации скорости е = ^V v + ( V v ) ^T J ^2 ;

• -    уравнение несжимаемости I_x ( е ) = V - v = 0 ;

• -    уравнение пластического течения Леви-Мизеса е = 3 £ S /( 2 ст ) ;

• -    условие пластичности Мизеса ст = ст .

В перечисленных уравнениях приняты следующие обозначения: V — оператор Гамильтона в текущей конфигурации; T — тензор напряжений Коши (истинных напряжений); е — тензор деформации скорости; v — вектор скорости перемещения произвольной точки слитка; I j ( е ) — первый инвариант тензора е ; S — девиатор тензора напряжений; ст, — предел текучести материала; ст — интенсивность напряжений ( ст = ^ ( 3/2 ) S -- S ); £ — интенсивность деформации скорости ( £ = ^ ( 2/3 ) е -- е ).

Предел текучести материала ( ст₅ ) является функцией накопленной интенсивности деформации ( £ ), интенсивности деформации скорости ( £ ) и абсолютной температуры ( T )

стs = стs(е,£,T),      £=|ёdt.

Для сплава Waspaloy предел текучести задается в виде таблицы в температурном интервале 954,5–1148,9 К для диапазона изменения интенсивности деформации скорости 0,032–1,000 с–1 и диапазона изменения интенсивности деформации 0–0,9. Именно в этих пределах изменения указанных величин осуществляется, как показано в работе [1], рассматриваемый технологический процесс. Величины T , £, е в процессе деформирования меняются от точки к точке. Поэтому, в зависимости от них, предел текучести ст, тоже будет отличаться от точки к точке. Например, при 1000°С, £ =0,35, £ = 0,032, предел текучести ст5

примерно 339,62 МПа. В таблице из библиотеки материалов программного комплекса Deform-2D/3D отсутствует значение предела текучести именно для температуры 1000°С. Его соответствующая величина найдена с помощью линейной интерполяции. Интерполяция и экстраполяция будут использоваться и далее при работе с указанной таблицей.

Для замыкания постановки краевой задачи записанные выше уравнения дополняются следующими граничными условиями: на части S поверхности S , ограничивающей текущий объем деформируемого тела V , задается скорость перемещения v = v * , а на части S — внешние силы: p * = N - T . Здесь полная текущая поверхность тела есть S = S _v и S_p .

Применение к уравнениям равновесия, несжимаемости и граничным условиям для напряжений, представленным в однородном виде, стандартной процедуры Галеркина, учет того, что области V и S не пересекаются и вариации 3 v и 5ст есть произвольные, не связанные между собой функции, приводят к выражению: