Численное исследование вибрационных процессов в композитных материалах с целью построения системы контроля расслоений

На сегодняшний день существует большое число различных методов наблюдения за изделиями в процессе их эксплуатации. Можно выделить два основных подхода к дефектоскопии: разрушающий и неразрушающий контроль. Методы разрушающего контроля способны обеспечивать надлежащее выполнение требований к качеству изделий при строительстве различных сооружений и дорог, в основном изготовленных из классических материалов (бетона, различных металлов), однако требуют вмешательства в структуру готового изделия и тем самым вызывают изменение его механических характеристик, что недопустимо для большинства применяемых конструкций. В свою очередь методы неразрушающего контроля осуществляют оценку целостности конструкции и не изменяют ее структуры [4], что делает данный класс методов наиболее подходящим для организации системы мониторинга на практике.

К методам неразрушающего контроля можно отнести различные визуальные методы, основной недостаток которых заключается в том, что они не позволяют обнаруживать повреждения, находящиеся за пределами зоны видимости [5]. Кроме того, на их эффективность существенно влияют навыки специалиста, проводящего инспекцию. Одним из важнейших подвидов неразрушающего контроля являются вибрационные методы, использующие возбуждаемые в конструкции колебания и регистрируемые с помощью различных датчиков параметры для идентификации дефектов в конструкции [6].

Вибрационные методы, в свою очередь, можно разбить на несколько подгрупп: 1) методы, в которых оценка состояния объекта наблюдения производится путем регистрации изменения модальных параметров (собственных частот, собственных форм, кривизны собственной формы и другого) [7, 8]; 2) методы, анализирующие волновые процессы, происходящие в исследуемом объекте [9-12]. Существует множество научных публикаций, посвященных вибрационным методам контроля, где описываются их основные достоинства и недостатки [13–17].

Создание любой системы дефектоскопии направлено на решение следующих задач:

• 1)    Определение наличия дефекта или повреждения в интересующем объекте.

• 2)    Нахождение местоположения дефекта.

• 3)    Выяснение размеров дефекта.

• 4)    Оценка остаточного ресурса изделия.

2. Постановка задачи

Настоящая статья посвящена применению вибрационных подходов дефектоскопии для установления факта расслоения композитной конструкции, а также местоположения и размеров дефекта с помощью анализа особых — характерных только для него — собственных частот и форм колебаний. Отличительная особенность рассматриваемых частот колебаний — существенное превышение по сравнению с остальной частью конструкции амплитуды колебаний в области расслоения. Внешнюю вынуждающую силу, необходимую для возбуждения данных форм колебаний можно обеспечить с помощью системы пьезоэлементов, размещенных на инспектируемой конструкции. Возможности предлагаемого подхода демонстрируются на численной конечно-элементной модели композитной пластины с расслоением. В постановке задачи учитываются диссипативные свойства материала, необходимые для достоверного моделирования вибрационных процессов.

Обнаружена сильная зависимость частот колебаний, характерных для дефекта в виде расслоения, от размера дефекта и слабая зависимость от местоположения, что дает возможность настраивать систему обнаружения повреждений на дефект определенного размера. Проведенное исследование показало, что предложенный подход может успешно применяться для обнаружения расслоения в композитных конструкциях.

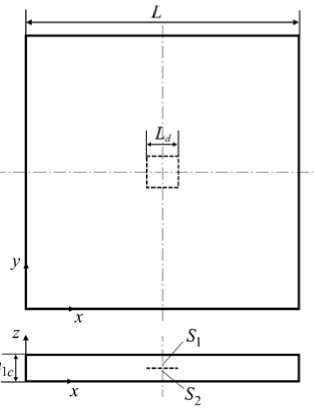
Рис. 1. Схема объекта исследования

В качестве контролируемого объекта рассмотрена квадратная пластина размером L = 300 мм из слоистого композитного материала (Рис. 1). Предполагается наличие n = 15 слоев по толщине пластины. Толщина одного слоя составляет h1 с = 0,26 мм, следовательно, толщина всей пластины равна h1 с n = 3,9 мм. Материал считается однородным упругим изотропным со следующими эффективными механическими характеристиками: E = 58 ГПа, v = 0,3, р = 1800 кг/м3. Слоистая структура материала учитывается только через геометрические размеры. В пластину внесен квадратный дефект в виде расслоения длиной Ld с границами S1 и S2 , располагающийся между 6-м и 7-м слоями композиционного материала. Геометрический центр расслоения совпадает с центром пластины.

Математическая постановка задачи формулируется в виде принципа возможных перемещений:

д2 и f o„8e,.dV - p —т-8udV = F,8udS. ij ij                           2 i                      i i

VV t   S

Здесь: а _ц = C_ijkl e _kl — компоненты тензора напряжений, C_ijkl — тензор упругих постоянных,

1 ГдU дuj )

е„ = — --+--— компоненты тензора деформаций, p — плотность материала пластины, и — j 2 дx - дх, I компоненты вектора перемещений,; Fi — компоненты вектора внешних поверхностных нагрузок. Границы расслоения считаются свободными от напряжений:

° zz I s i , S 2

I S ,, S ₂      ° zy[

= о.

S ₁, S ₂

Численные эксперименты выполнены с применением пакета конечно-элементного анализа ANSYS. Так как рассматриваются колебания в плоскости, перпендикулярной плоскости пластины, то при построении численной модели использовался объемный конечный элемент с квадратичной аппроксимацией перемещений, что позволяет наиболее достоверно описывать данный тип колебаний. Выбор объемного конечного элемента обусловлен удобством моделирования расслоения на разной глубине и возможностью внесения в математическую модель нескольких расслоений между различными слоями. Параметры конечно-элементной сетки подбирались таким образом, чтобы в зоне дефекта на одну грань квадратного расслоения приходилось не менее пяти элементов. Узлы конечно-элементной сетки в зоне расслоения, принадлежащие поверхностям S ₁ и S ₂ , геометрически совпадали, но не были связаны друг с другом.

На рисунке 2 показано поперечное сечение модели пластины с расслоением при изгибных колебаниях.

Рис. 2. Вид поперечного сечения численной модели пластины с расслоением при изгибных колебаниях

Конечно-элементная постановка задачи в матричной форме имеет следующий вид:

Mu + Cu + Ku = F( t), где M — матрица масс системы, C — матрица демпфирования, K — матрица жесткости системы, F(t) — функция нагрузки, зависящая от времени, u — вектор узловых перемещений, u — вектор узловых скоростей, u — вектор узловых ускорений.

Для исследования динамического поведения пластины с расслоением применялись два типа колебаний: собственные колебания, необходимые для нахождения характерных для такого дефекта частот и изучения форм колебаний, соответствующих этим частотам; вынужденные установившиеся колебания, позволяющие проверить возможность возбуждения колебаний с повышенной амплитудой в области дефекта с помощью внешнего периодического воздействия с частотой, полученной из модального анализа.

Необходимым условием при решении задачи о собственных колебаниях является отсутствие внешних воздействий F = 0. Движение точек системы происходит по гармоническому закону. Таким образом, уравнение перемещений для каждой точки будет иметь вид:

и ( X, t) = и max cos(to t + ф) , где иmax — максимальная амплитуда, ю = 2пи — угловая частота колебаний, и — линейная частота колебаний, t — время, ф — фазовый сдвиг. В конечно-элементном виде задача формулируется следующим образом:

(К -ю2М)u0 = 0 , где u0 — собственные формы колебаний.

При анализе вынужденных установившихся колебаний возможен учет демпфирования системы. Сделать это можно с помощью комплексного динамического модуля. В этом случае вектор внешней периодической вынуждающей нагрузки представляется в виде:

* (™ t+ф) max e где Fmax — максимальная амплитуда.

Учет вязкоупругих свойств материала для расчета вынужденных установившихся колебаний посредством динамического комплексного модуля в пакете ANSYS задается как сумма

E * = E'+ iE", где E ' — модуль накопления, описывающий способность материала к аккумулированию энергии, E '' — модуль потерь, характеризующий рассеивание материалом энергии.

Комплексный динамический модуль связан с тангенсом потерь (tan( ф) ) следующим соотношением:

E * = E ' + iE " = E '(1 + i —) = E '(1 + i tan( ф)) . E '

Движение точек системы описывается гармоническим законом

u = u

max

„ i ф i to t е ^ф e

или u = (ureal + 1 uimag ) e"t , где ureal и uimag — действительная и мнимая части вектора перемещений. Амплитуда перемещений в каждом узле равна umax =   (ureal ) + (uimag ) .

• 3.    Анализ собственных форм колебаний

Один из самых распространенных вибрационных подходов дефектоскопии основан на анализе сдвига собственных частот колебаний при появлении дефекта и росте его размеров. Однако изменение собственных частот колебаний лишь сигнализирует о нарушении сплошности, но не дает ответа на вопрос, где это произошло. Иными словами, подход [18], опирающийся на регистрацию изменения собственных частот колебаний эффективен для решения первого пункта общей задачи дефектоскопии (см. Введение). Но не менее важен вопрос о местоположении дефекта в конструкции.

Следует заметить, что при возникновении расслоения вместе с собственными частотами претерпевают изменения и собственные формы колебаний. Численное исследование форм колебаний позволило установить, что при наличии расслоения — самого распространенного из дефектов в слоистых композитных конструкциях, для системы свойственно существование особенных собственных частот и характерных для них собственных форм. Главной отличительной особенностью таких форм является значительное увеличение амплитуды колебаний в зоне дефекта (Рис. 3).

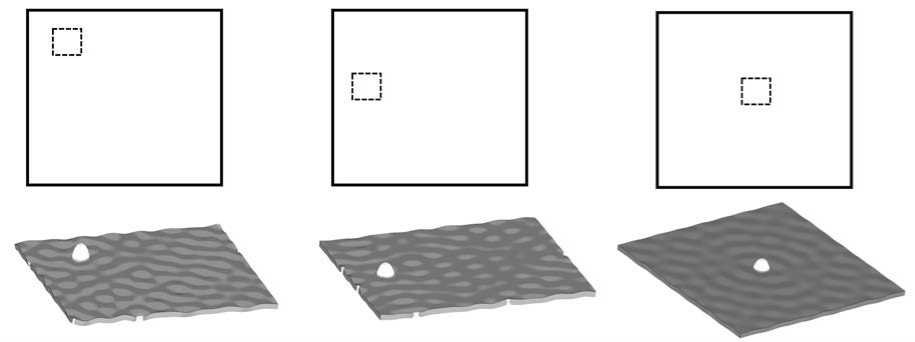
Рис. 3. Собственные формы колебаний при различном местоположении расслоения на пластине

Появление специфических форм колебаний обусловлено падением жесткости в зоне дефекта при образовании расслоения. В результате слоистая конструкция оказывается локально разделенной на две или более частей, слабо взаимодействующих друг с другом. В этом случае область дефекта можно условно рассматривать как пластину с жестким закреплением по контуру. Частота, соответствующая этим формам колебаний, определяется размером дефекта и механическими характеристиками материала.

Для реальных конструкций желательно обнаружение дефекта на ранней стадии его развития, когда он еще мал и не представляет угрозу для эксплуатируемого объекта. Частота колебаний дефекта находится в обратно пропорциональной зависимости от его размеров, поэтому для обнаружения небольших расслоений необходимо генерировать в конструкции колебания с высокими, в несколько десятков килогерц, частотами. В изотропном приближении для приведенной модели пластины при модуле упругости E = 58 ГПа частота колебаний дефекта размерами 10x10 мм равна 107 кГц.

Анализ форм колебаний с описанными частотами выявил несколько их отличительных особенностей: так, такая частота слабо обусловлена местоположением дефекта в конструкции. У объекта в виде пластины 300x300 мм частота колебаний, характерная для дефекта, практически не изменяется в зависимости от местоположения расслоения при условии свободных границ пластины. Также наблюдается слабая связь этой частоты с размерами самой конструкции. Подобные проявления очевидны в силу того, что материал вне дефекта выступает в роли заделки зоны расслоения. Постоянство таких частот делает их привлекательными для методов дефектоскопии с использованием вибрационных подходов.

В реальной конструкции для возбуждения колебаний определенного рода необходимо прикладывать внешнюю нагрузку. Инициирование колебаний с повышенной амплитудой в зоне дефекта должно осуществляться внешним периодическим воздействием с частотой, характерной для дефекта, найденной из модального анализа. Проведенные численные эксперименты позволили исследовать возможность возбуждения колебаний в зоне дефекта и выявить параметры, влияющие на эффективность обнаружения дефекта описанным методом.

• 4.    Возбуждение колебаний в области расслоения

На примере собственных частот и форм колебаний удалось показать, что для дефекта в виде расслоения существуют особые частоты и соответствующие им формы колебаний. Для изучения возможности возбуждения таких форм колебаний и обнаружения повреждений при вынужденных установившихся колебаниях рассмотрена задача, в которой частота вынуждающей силы равнялась полученной из анализа собственных частот колебаний. Предполагается, что в системе мониторинга конструкции, основанной

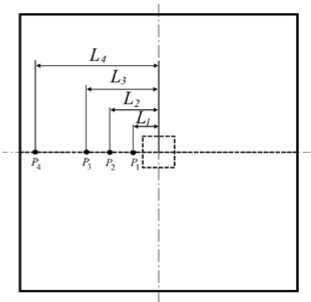
Рис. 4. Различное размещение точек приложения внешнего периодического воздействия

на предлагаемом подходе, источником внешнего воздействия будут выступать встроенные пьезоэлементы. На текущем этапе вычислений к узлам конечно-элементной сетки с определенными координатами прикладывалась сила с амплитудой 10 кН. В ходе исследования точки приложения внешнего периодического воздействия P 1 , ..., P 4 располагались на разном удалении L_i от местоположения дефекта, мм: 23; 43; 63; 103 (Рис. 4). При каждом расчете сравнивалось распределение по выделенной пунктиром линии компоненты перемещений u_z исходной пластины без дефекта и пластины, содержащей центрально расположенное расслоение размерами 10x10 мм.

внутренней диссипации контролируемого

Одним из основополагающих параметров, необходимых для достоверного описания вынужденных колебаний конструкции, является внутреннее демпфирование. Правильное определение и учет при численном моделировании параметров, отвечающих за механизмы объекта, дают возможность принять во внимание такие особенности поведения конструкции, как затухание колебаний по мере удаления от области дефекта места приложения внешней периодической нагрузки.

Определение диссипативных характеристик композита осуществлялось на основе анализа затухания свободных колебаний пластинки [19]. Пластинка подвешивалась на мягких резиновых нитях, что обеспечивало практически беспрепятственное ее движение. С одной стороны конструкция облучалась звуковыми волнами с частотой 1 кГц, а с другой — выполнялось измерение нормальной компоненты скорости с помощью портативного лазерного виброметра (Polytec PDV100) с частотой дискретизации 48 кГц. Экспериментальная установка показана на рисунке 5 а .

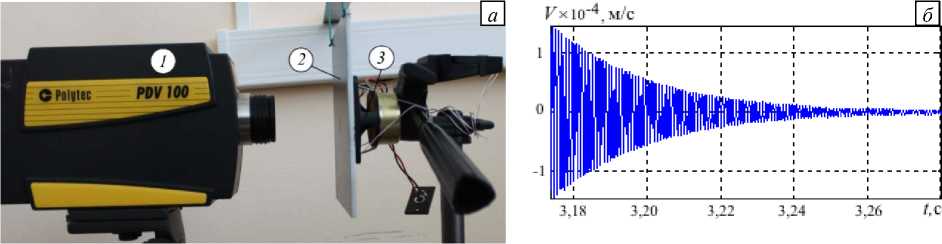
Рис. 5. Экспериментальная установка ( а ), где 1 – виброметр; 2 – пластина; 3 – динамик, и вид нормальной компоненты скорости в измеряемой точке пластины на стадии затухания ( б )

Возбуждение выполнялось в течение одной секунды, после этого пластина совершала свободно затухающие колебания (Рис. 5 б ). Скорость затухания характеризуется логарифмическим декрементом, который составлял 6,2. На основе математической модели определялся параметр β= 8 ⋅ 10 ^{- 7} , соответствующий этому декременту. Параметр β задает механизм диссипации σ ^ij = β С ^ijkl ∂ε ^kl ∂ t . Тангенс угла механических потерь выражается через β как tan( ϕ ) = 2 π f β и имеет значение 77 ⋅ 10 ^{- 3} . Здесь f — собственная частота колебаний пластины.

Имеющаяся в распоряжении авторов данной работы аппаратная база позволила определить диссипативные характеристики материала при частоте колебаний 1 кГц. Численные расчеты проведены в приближении независимости комплексного динамического модуля от частоты колебаний. В дальнейшем планируется использовать новое оборудование для идентификации диссипативных свойств материала при более высоких частотах колебаний.

На рисунке 6 а изображено поле перемещений u_z рассматриваемой пластины с расслоением, полученное из решения задачи о вынужденных установившихся колебаниях. В силу учета механизмов внутренней диссипации происходит не мгновенное распространение возбуждения от места приложения внешней нагрузки, которое, приходя в область дефекта, вызывает колебания расслоения большой амплитуды. Распределение амплитуды перемещений по линии, проходящей через центр расслоения, представленное на рисунке 6 б , демонстрирует существенное увеличение по сравнению с целой конструкцией амплитуды колебаний в области расслоения. Важным фактором является частота внешнего возбуждения, которая должна приводить к формированию волн с длиной, сопоставимой с размерами дефекта. В противном случае при длинах волн, превосходящих данный размер, возбуждение колебаний повышенной амплитуды в области дефекта не возможно, а, следовательно, не возможна и его идентификация.

Такая ситуация изображена на рисунке 7. В данном случае модуль упругости материала занижен, в результате чего уменьшилась и собственная частота, характерная для дефекта (с 107 до 50 кГц). После приложения внешней нагрузки на полученной частоте и проведения численного расчета вынужденных установившихся колебаний не происходит возбуждения колебаний высокой амплитуды в области дефекта, так как длина волны на такой частоте превосходит размер дефекта и огибает его при прохождении. На рисунке 7 б видно незначительное отличие в распределении перемещений в окрестности расположения расслоения (вблизи координаты х = 0). Однако отличие слишком мало, чтобы идентифицировать наличие дефекта.

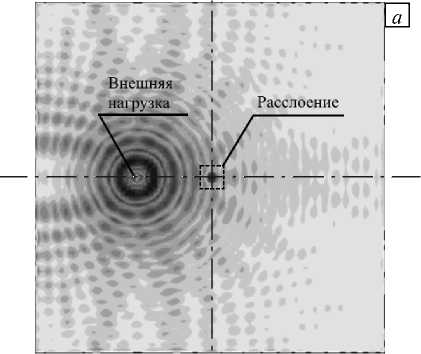
Рис. 6. Поле перемещений u_z в пластине с расслоением при вынужденных установившихся колебаниях на резонансной частоте дефекта ( а ) и распределение амплитуды перемещений u_z по линии, проходящей через центр расслоения ( б )

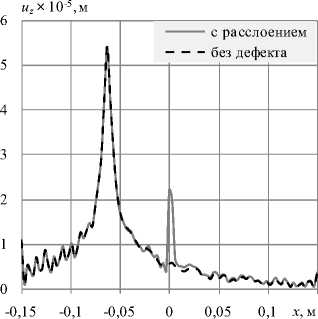
Рис. 7. Поле перемещений u_z в пластине с расслоением при вынужденных установившихся колебаниях в случае, когда длина волны превышает размер дефекта ( а ), и распределение амплитуды перемещений u_z по линии, проходящей через центр расслоения ( б )

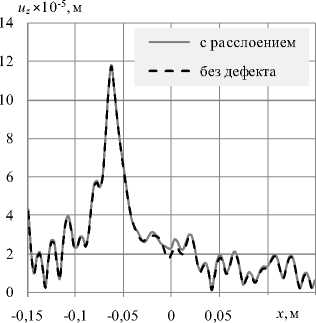
Далее приведены распределения амплитуды перемещений u_z , аналогичные графику на рисунке 6 б , для разных мест приложения внешнего периодического воздействия (Рис. 8). На графиках сплошной линией обозначены результаты, полученные для пластины с расслоением, пунктирной — для целой пластины без дефекта.

Из сравнения распределений для пластин с дефектом и исходной (целой) видно, что амплитуда измеряемого параметра в зоне дефекта существенно превышает амплитуду для бездефектной конструкции.

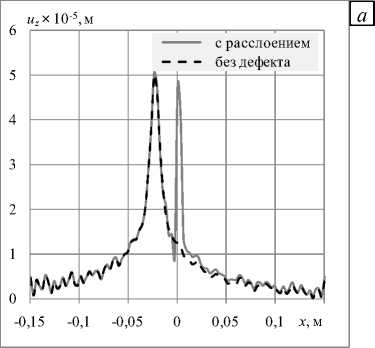
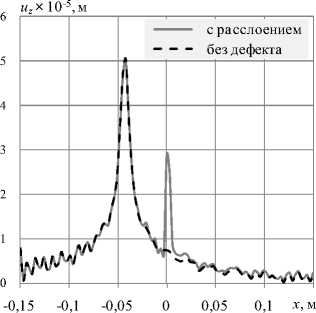
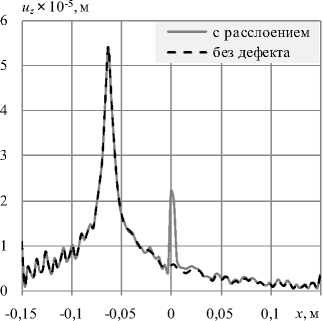
Рис. 8. Распределение по линии, проходящей через центр расслоения, амплитуды перемещений u_z для разных по отношению к геометрическому центру пластины положений точки приложения внешнего периодического воздействия, мм: 23 ( а ); 43 ( б ); 63 ( в ); 103 ( г )

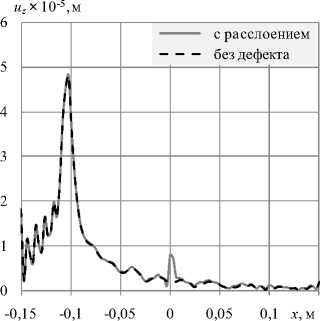
Графики разности A u = и _д - u o , где и _д и u _o — соответственно амплитуда перемещений для модели с дефектом и без дефекта, и отношения перемещений для двух типов пластин, представленные на рисунках 9 и 10 для точки приложения внешнего воздействия на расстоянии 63 мм от центра дефекта, наглядно демонстрируют изменение измеряемой величины в области дефекта. Штрихпунктирной линией на рисунках обозначена зона расслоения.

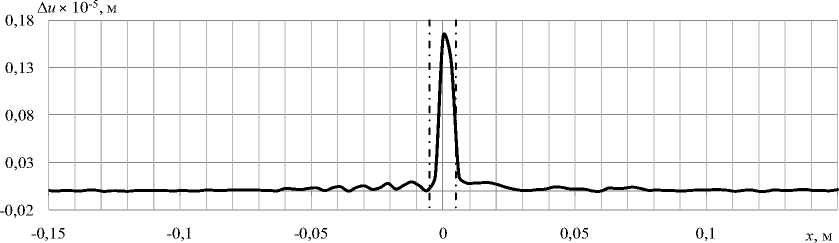
Рис. 9. График разности компоненты перемещений u_z в пластине с расслоением и в бездефектной пластине

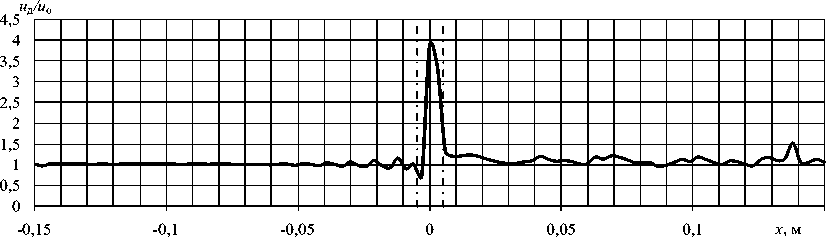
Рис. 10. График отношения компоненты перемещений u_z в пластине с расслоением к соответствующей компоненте в бездефектной пластине

Вне области расслоения измеряемые параметры как бездефектной конструкции, так и конструкции с дефектом практически не изменяются, что дает возможность, помимо расположения, оценить и размеры дефекта. При этом прослеживается уменьшение отличия в перемещениях дефектной и бездефектной конструкций в зоне расслоения по мере удаления точки приложения внешнего периодического воздействия от местоположения дефекта.

Анализ характера амплитуд перемещений целой пластины и пластины с дефектом показал, что отношение амплитуд сохраняется (в области расслоения амплитуда измеряемой величины увеличивается приблизительно в 3,8 раз по отношению к целой пластине), а разность уменьшается по мере удаления точки нагружения от дефекта. Этот результат продемонстрирован на рисунке 11 для компонент перемещений u_z .

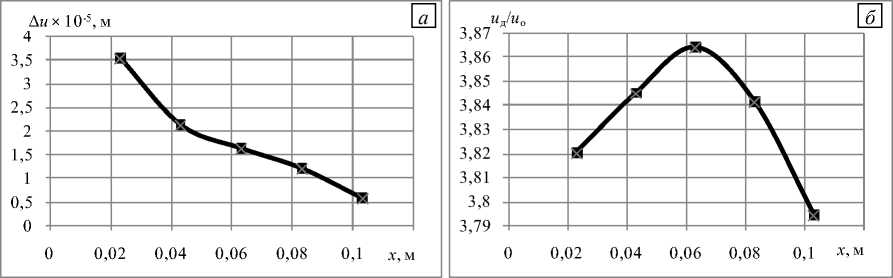
Рис. 11. Изменение разности ( а ) и отношения перемещений ( б ) в дефектной и бездефектной пластинах в зависимости от удаленности точки приложения внешнего периодического воздействия от центра дефекта

В силу гипотезы об отсутствии контактного взаимодействия берегов расслоения, используемой при построении численной модели, полученные результаты носят не количественный, а только качественный характер и требуют дальнейшей экспериментальной верификации. Взаимодействие смежных поверхностей друг с другом может привести к уменьшению амплитуды колебаний в области дефекта, но, тем не менее, ее величина останется выше величины амплитуды колебаний бездефектной части конструкции, и эффективность регистрации отличия этих амплитуд будет зависеть от чувствительности измерительной системы.

• 5.    Выводы

В рамках представленной работы проведено численное исследование собственных частот и форм колебаний, характерных для дефекта в виде расслоения в слоистых композитных материалах. Результаты расчетов показали значительное увеличение амплитуды колебаний в области дефекта для таких частот, а также слабую зависимость от его местоположения, что делает эти частоты удобными для реализации вибрационного метода дефектоскопии, основанного на возбуждении резонансных колебаний в области расслоения с частотой вынуждающей силы, полученной из модального анализа.

Выполнен анализ эффективности возбуждения колебаний повышенной амплитуды в области дефекта при удалении точки приложения внешней вынуждающей силы от местоположения дефекта. Результаты исследования показали применимость данного подхода для обнаружения и локализации местоположения дефекта, а также оценки его размеров.

Предлагаемый метод контроля дефектов позволяет обосновать возможность создания на основе вибрационных процессов системы контроля расслоений в композитных материалах и определить ее основные параметры.

Работа выполнена при финансовой поддержке РФФИ (проект № 16-31-00305-мол_а).