Численное исследование влияния дефектов зубного ряда малой протяженности на напряженно-деформированное состояние мостовидного протеза и периодонта

Своевременно незамещенные дефекты зубных рядов сопровождаются вторичными деформациями, проявляющимися в наклоне зубов в сторону дефекта зубного ряда [4, 7]. По разным причинам подобная патология затрудняет использование несъемных конструкций зубных протезов. При наклоне зуба зона его безопасного препарирования уменьшается, что увеличивает риск повреждения пульпы зуба [17, 29, 31]. В связи с этим существует практика предварительного депульпирования опорных зубов [8], однако такая врачебная тактика формирует риск возникновения эндодонтических осложнений (недостаточная обтурация каналов или необнаружение дополнительных каналов [1, 5, 6, 35]). Помимо прочего, в ситуациях © Крупнин А.Е., Харах Я.Н., Киракосян Л.Г., Золотницкий И.В., Арутюнов С.Д., 2019

Харах Ясер Насерович, ассистент кафедры пропедевтики стоматологических заболеваний, Москва Киракосян Левон Гамлетович, старший лаборант кафедры пропедевтики стоматологических заболеваний, Москва

Золотницкий Игорь Валерьевич, д.м.н., профессор кафедры ортопедической стоматологии, Москва Арутюнов Сергей Дарчоевич, д.м.н., профессор, заведующий кафедры пропедевтики стоматологических заболеваний, Москва с использованием наклоненных зубов в качестве опорных необходимо учитывать распределение жевательного давления и напряженно-деформированное состояние самой ортопедической конструкции. Исследователи сходятся во мнении, что степень наклона опорных зубов влияет на их функциональную выносливость, однако данные о пределах допустимых значений углов наклона зубов сильно разнятся и находятся в диапазоне от 24° [35] до 70° [18, 23, 24], что обусловлено различными постановками задач исследований. В своих теоретических расчетах Tylman [38] и Linkow [26] основывались на перераспределении жевательного давления относительно оси зуба. Hood и др. [19, 20, 39] с помощью поляризационно-оптического метода и метода двухмерного математического моделирования проводили сравнительный анализ напряженно-деформированного состояния костной ткани при замещении малого дефекта зубного ряда в ситуациях с ненаклоненным и наклоненным на 30° моляром. Позднее Jia [20] провела аналогичное исследование состояния костной ткани, окружающей опорный наклоненный зуб методом конечных элементов, чем подтвердила результаты исследования Hood. В ходе пятилетнего клинического наблюдения пациентов с замещенными малыми дефектами зубных рядов, осложненных наклоном опорных зубов не более чем на 50 градусов, с помощью несъемных ортопедических конструкций исследователями Ning и др. [28] отмечен высокий процент успеха ортопедического лечения (89%).

Результаты вышеописанных исследований не определяют четкие границы показаний, так как в каждой работе рассматриваются определенные биомеханические аспекты без учета других. Например, отсутствуют исследования, в которых бы рассматривались вариации наклона медиального опорного зуба одновременно с дистальным, что также встречается в клинической практике. Важно также отметить, что вопрос учета цемента в математической модели до сих пор остается открытым. Одна из причин заключается в том, что наличие в конечно-элементной сетке тонкого слоя цемента приводит к значительному повышению размерности задачи и, как следствие, времени расчета.

Данная работа является продолжением исследований [3], направленных на создание методологии расчета и проектирования мостовидных протезов, в ней устанавливается связь между напряженно-деформированным состоянием мостовидного протеза из полиметилметакрилата при наклоне первого премоляра и моляра в сторону отсутствующего второго премоляра, исследуется влияние наклона зубов на нагрузки, воспринимаемые периодонтом, обсуждаются применяемые для оценки прочностных свойств теории прочности. Полученные результаты сопоставляются с результатами для витальных зубов. Решается задача оценки влияния слоя цемента в модели на напряженно-деформированное состояние мостовидного протеза.

Методы и материалы

Теоретические сведения

Разрешающее уравнение метода конечных элементов при решении статических задач имеет вид [2]

Ku = f , (1)

где K – матрица жесткости, u – вектор узловых перемещений, f – вектор узловых сил. Это классическое уравнение применяется при решении задач, когда силы, действующие на систему, не зависят от времени или являются медленно меняющимися функциями времени. В предыдущем исследовании [3] было установлено, что динамические эффекты ярко проявляются при кратковременных воздействиях на биомеханическую систему. По мере увеличения времени действия силы (уже на уровне 0,03 с) разница между результатами статического и динамического анализа становится незначительной. Поэтому для решения поставленных задач использовался статический подход к оценке напряженно-деформированного состояния имплантата, периодонта и цемента. Известно [9], что в случае сложного напряженного состояния оценку прочностных свойств можно проводить по одной из известных теорий прочности. Широкое распространение при решении задач биомеханики получила теория Хубера– Мизеса (далее – теория Мизеса), эквивалентные напряжения по которой определяются следующим образом:

σ экв

2 |_ ( ° 1 - ° 2

)2 + ( G

-

σ3

^{) 2 +(} ° 1

-

° 3 ) 2 ,

где σ ₁ , σ ₂ и σ ₃ – главные напряжения.

Эта теория не учитывает различие в значениях предельных характеристик материалов. Однако известно [36], что для стоматологических цементов предел прочности при растяжении ст В Р и предел прочности при сжатии (Г В С могут сильно различаться. В этом случае корректно использовать теорию прочности Мора, эквивалентные напряжения по которой определяются следующим образом:

°экв = °1 - W3, где

V =

σ _{В Р}

σ В С

– отношение предела прочности при растяжении к соответствующему

пределу при сжатии. Это соотношение использовалось для определения эквивалентных напряжений в слое полимерного цемента. Задача оценки прочностных свойств периодонтальной связки в условиях сложного напряженного состояния является трудной. Причина заключается в том, что не существует единой методики определения механических свойств данной ткани. Необходимо учитывать и тот факт, что на свойства биологических объектов, каковым является периодонт, оказывает влияние ряд факторов (образ жизни, возраст, заболевания и т.д.). Имеющиеся в литературе сведения [16, 21] говорят о широком диапазоне изменения упругих характеристик периодонта: 0,01–1750 МПа для модуля упругости первого рода, 0,28–0,49 для коэффициента Пуассона. Очевидная сложность также заключается в определении механических характеристик периодонта при сжатии. Таким образом, авторами проведена оценка эквивалентных напряжений, возникающиих в периодонте как по теории Мизеса, так и по теории наибольших нормальных напряжений, которая формулируется следующим образом:

° экв = ° 1 -

Значения эквивалентных напряжений, полученные с использованием теорий прочности Мизеса и наибольших нормальных напряжений, будут ориентиром при сравнении с экспериментальными значениями прочности при одноосном растяжении периодонта, полученными в работе [15]: 3,9 МПа.

Геометрия модели

Объекты исследования представлены мезиодистальными сечениями участка нижней челюсти, включающего первый премоляр и первый моляр, мостовидный протез с опорой на первый премоляр и первый моляр, промежуточную часть – фасетку (недостающий второй премоляр), слой цемента, эмаль, дентин, кортикальную и губчатую кости, периодонт и пульпу (рис. 1). Геометрия зубов получена по результатам компьютерной томографии с последующим воссозданием трехмерных моделей и мезиодистальным срезом.

F = 67 Н F = 33 Н

F = 100 Н

Губчатая кость

Дентин

Кортикальная кость

Периодонт

Полиметилметакрилат

Полимерный цемент

Пульпа

Эмаль

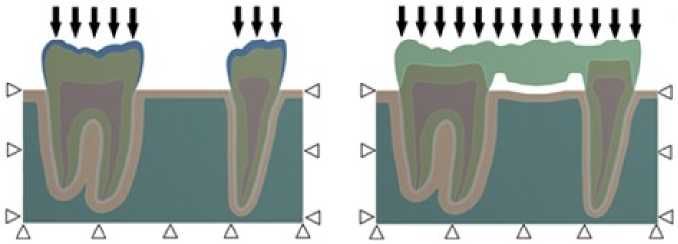
Рис. 1. Геометрия модели, нагрузка и граничные условия

Подробно геометрические параметры модели освещены в [3]. Угол наклона премоляра менялся в диапазоне от 0° (исходное положение) до 15° с шагом в 5°, моляра – от 0° (исходное положение) до 25° с шагом в 5°. Для оценки влияния цемента на результаты расчетов использовались три значения толщины слоя: 60; 80 и 100 мкм. Для удобства визуализации результатов введем следующую систему представления расчетного случая: α – β, где α – угол наклона моляра, β – угол наклона премоляра. В рамках решения задачи были рассмотрены следующие варианты положения зубов: 0–0, 5–0, 10–0, 15–0, 20–0, 25–0, 0–5, 0–10, 0–15, 5–5, 10–10, 15–15, 20–15, 25–15.

Нагрузки и граничные условия

Для решения задачи определения напряженно-деформированного состояния в мостовидном протезе, слое цемента и окружающем периодонте к окклюзионной поверхности приложена вертикальная распределенная нагрузка, равнодействующая которой равна F = 100 Н (рис. 1). Нагрузка, приходящаяся на витальные премоляр и моляр, определялась из отношения площадей контактной поверхности (в плоском случае речь идет о линиях) при суммарной действующей окклюзионной нагрузке F = 100 Н. Это отношение составило 1:2, поэтому нагрузка, приходящаяся на премоляр, составила F 1 = 33 Н, на моляр – F 2 = 67 Н (рис. 1). На границы расчетной области наложены кинематические граничные условия, соответствующие нулевым перемещениям [26, 38].

Конечно-элементная модель

Задача решалась в плоско-деформированной постановке [10, 12–14, 22, 25, 30, 33, 34, 36]. Разбиение модели на конечные элементы и численное решение проводилось в программном пакете ANSYS . После теста на сходимость окончательное число 6-узловых [30] элементов PLANE 183 составило 34 814 для модели витальных зубов, 63 289 для геометрии без учета цемента и 441 550 элементов в случае учета цемента. При рассмотрении геометрических конфигураций в условиях наклона зубов число элементов менялось незначительно. Конечно-элементные модели представлены на рис. 2.

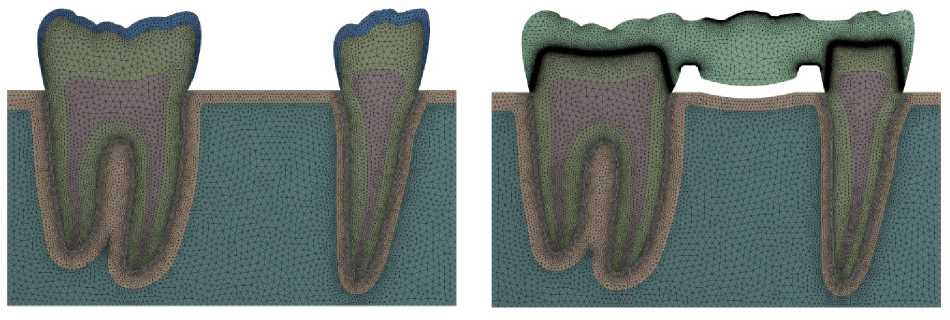
Рис. 2. Конечно-элементные модели

Размер элементов в областях концентрации напряжений и слое цемента – 0,005 мм. Качество сетки контролировалось средними значениями параметров Element quality = 0,95, Skewness = 9,58∙10^–2 и Orthogonal quality = 0,94.

Полиметилметакрилат, твердые и мягкие ткани зубов и нижней челюсти в процессе моделирования предполагались однородными, изотропными и линейноупругими [15, 41, 42]. Механические свойства материалов взяты из [11, 28, 32, 36, 42] и представлены в табл. 1.

Таблица 1

Механические свойства материалов

Материал	Модуль Юнга Е , МПа	Коэффициент Пуассона µ	Предел прочности при растяжении, МПа	Предел прочности при сжатии, МПа
Кортикальная кость	12 200	0,26	–	–
Губчатая кость	1220	0,31	–	–
Дентин	18 600	0,31	–	–
Пульпа	2	0,45	–	–
Периодонт	70	0,45	–	–
Полиметилметакрилат	3000	0,38	–	–
Полимерный цемент	2400	0,4	50	220
Эмаль	84 100	0,2	–	–

Результаты

Напряжения в слое цемента

На рис. 3 представлены зависимости максимальных эквивалентных по Мизесу напряжений, возникающих в мостовидном протезе, максимальных эквивалентных по Мору напряжений и максимальных сдвиговых напряжений в цементе в зависимости от толщины слоя цемента.

Наличие слоя цемента при оценке напряженно-деформированного состояния значительно увеличивает размерность задачи, но не влияет на эквивалентные напряжения в имплантате. Однако учет цемента может быть произведен для оценки

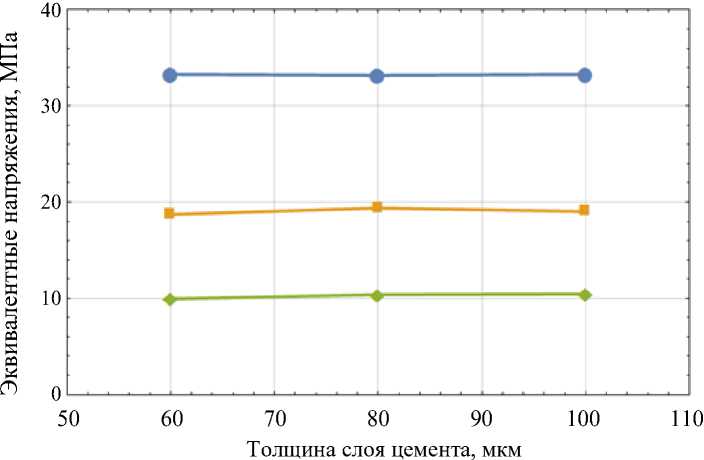
Рис. 3. Зависимость максимальных эквивалентных по Мизесу напряжений в протезе (синий график), максимальных эквивалентых по Мору напряжений (оранжевый график), максимальных сдвиговых напряжений (зеленый график) в цементе

напряжений, возникающих в нем при действии окклюзионных нагрузок. Если эквивалентные напряжения не достигают предела прочности при растяжении, то цемент можно не учитывать в дальнейших расчетах.

Напряжения в мостовидном протезе

На рис. 4 представлена зависимость максимальных эквивалентных по Мизесу напряжений, возникающих в мостовидном протезе.

о со S о к о 3 К н к о и к и и m

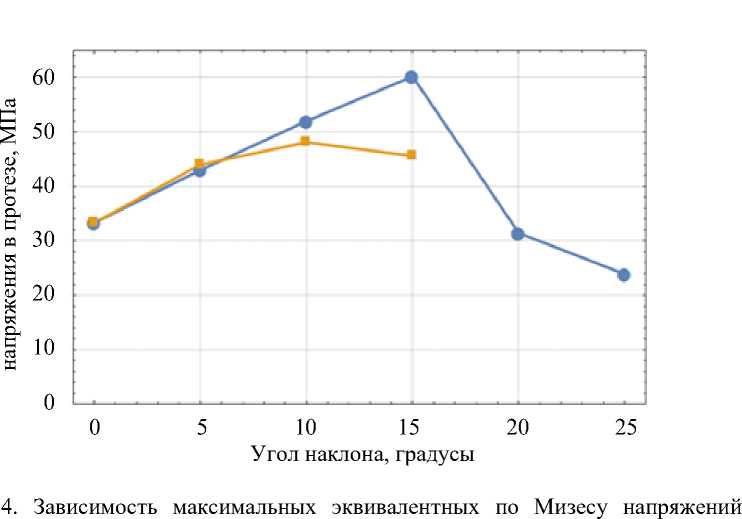
Рис.

в протезе при схеме α = var – β = 0 (синий график) и α = 0 – β = var

(оранжевый график)

В табл. 2 представлены максимальные эквивалентные по Мизесу напряжения в протезе для случаев наклона обоих зубов.

Таблица 2

Максимальные эквивалентные по Мизесу напряжения в протезе в случае наклона моляра и премоляра

Схема α = var – β = var	Максимальные эквивалентные по Мизесу напряжения, МПа
5–5	35,3
10–10	34,5
15–15	33,9
20–15	31,4
25–15	29,9

Максимальные напряжения, равные 60,2 МПа, возникают на окклюзионной поверхности в случае наклона моляра на 15–0, что меньше предела текучести полиметилметакрилата на 7%. При использовании мостовидного протеза в случае наклона в сторону дефекта как премоляра, так и моляра наблюдается уменьшение максимальных эквивалентных напряжений, возникающих в имплантате. Это связано с уменьшением длины протеза при наклоне зубов. В критическом случае 25–15° значение максимальных эквивалентных по Мизесу напряжений в имплантате равно 29,9 МПа, что составляет 46% от предельного значения.

Эквивалентные напряжения в периодонте

На рис. 5 представлена зависимость максимальных эквивалентных напряжений, возникающих в периодонте премоляра и моляра в случаях наклона премоляра α = 0 – β = var.

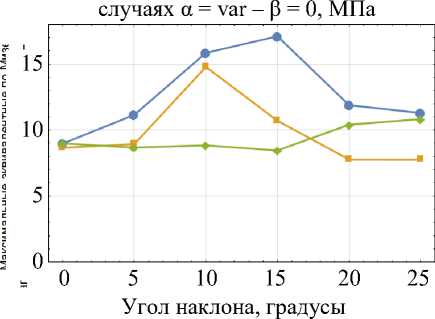
На рис. 6 представлена зависимость максимальных эквивалентных по Мизесу напряжений, возникающих в периодонте витального моляра и моляра, являющегося опорным для мостовидного протеза (угол наклона премоляра равен 0°).

Максимальные эквивалентные по

Мизесу напряжения в периодонте в

а

Максимальные эквивалентные по

Мизесу напряжения в периодонте в

б

Рис. 5. Зависимость максимальных эквивалентных напряжений в периодонте витального премоляра (синий график), премоляра, являющегося опорным (оранжевый график), и моляра, являющегося опорным (зеленый график), по теории Мизеса ( а ) и теории наибольших нормальных напряжений ( б )

Таблица 3

Схема α = var – β = var	Витальные		Опорные		Разгрузка, %
	моляр	премоляр	моляр	премоляр	моляр	премоляр
Максимальные эквивалентные по Мизесу напряжения, МПа
5–5	11,2	6,7	8,4	7,0	25	4
10–10	15,9	8,5	12,0	7,3	24	14
15–15	17,1	8,4	10,7	7,1	37	15
20–15	11,9	8,4	9,5	8,6	20	2
25–15	11,3	8,4	7,4	8,3	34	1
Максимальные главные напряжения, МПа
5–5	6,9	2,1	4,3	2,7	38	22
10–10	7,8	5,1	4,7	2,9	39	43
15–15	8,7	4,6	5,1	2,8	41	39
20–15	6,2	4,6	5,5	3,2	11	30
25–15	5,6	4,6	4,6	3,1	28	33

Максимальные эквивалентные по

Мизесу напряжения в периодонте в

а

Максимальные эквивалентные по Мизесу напряжения в периодонте в

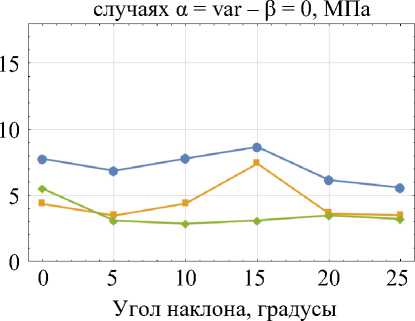
б

Рис. 6. Зависимость максимальных эквивалентных напряжений в периодонте витального моляра (синий график), моляра, являющегося опорным (оранжевый график), и премоляра, являющегося опорным (зеленый график), по теории Мизеса ( а ) и теории наибольших нормальных напряжений ( б )

Максимальные эквивалентные напряжения в периодонте в случае наклона моляра и премоляра

Результаты расчета свидетельствуют от том, что при наклоне премоляра (схема α = 0 – β = var) нагрузка на периодонт после установки мостовидного протеза возрастает при β < 10°, но при β > 10° напряжения в периодонте опорного премоляра выходят на уровень напряжений витального зуба и в дальнейшем снижаются. При наклоне моляра (схема α = var – β = 0) напряжения в периодонте опорного моляра на всем интервале изменения угла наклона меньше напряжений в периодонте витального моляра. Эквивалентные по Мизесу напряжения в премоляре для данной схемы незначительно возрастают, в то время как по теории наибольших нормальных напряжений – снижаются. Данные результаты согласуются с результатами [19]. В табл. 3 представлены максимальные эквивалентные напряжения в периодонте для случаев наклона обоих зубов.

Результаты показывают, что различия в значениях эквивалентных напряжений, посчитанных по разным теориям, существенны. Полученные по теории Мизеса напряжения в периодонте значительно превосходят предельные экспериментальные значения для периодонта моляра и премоляра [15], максимальное из которых составило 3,9 МПа. Однако для однозначного ответа о применимости той или иной теории необходимо исчерпывающее руководство для механических испытаний, учитывающее нелинейное поведение периодонта при больших значениях действующих сил. Анализ результатов свидетельствует о том, что установка мостовидного протеза в случаях наклона обоих зубов в сторону дефекта в целом позволяет снизить нагрузку на периодонт премоляра (до 43%) и моляра (до 41%) по сравнению с витальными наклоненными зубами.

Выводы

Вопрос о протезировании наклоненных зубов является острым и актуальным в стоматологии и ортопедии не только с позиции прочности имплантата, но и с позиции влияния на биологическую ткань – периодонт. В работе показано, что при действии распределенной окклюзионной нагрузки эквивалентные по Мизесу напряжения в протезе не превышают предела текучести материала. Увеличение наклона зубов в сторону дефекта уменьшает длину фасетки и, следовательно, напряжения в протезе в целом. С другой стороны, установка мостовидного протеза в случаях наклона обоих зубов позволяет снизить нагрузку на периодонт по сравнению с витальными зубами, что является важным результатом. Остается открытым вопрос о целесообразности применения той или иной теории для оценки прочности периодонта. Однако полученные авторами результаты показывают, что значения по теории Хубера–Мизеса значительно превосходят предельные экспериментальные значения – 3,9 МПа. Результаты, полученные по теории наибольших нормальных напряжений, больше соответствуют экспериментальным результатам. Отсутствие необходимости учета цемента в задачах исследования напряженно-деформированного состояния мостовидного протеза также является важным результатом, так как это обоснованное допущение значительно снижает размерность задачи и, как следствие, время расчета.