Численное исследование влияния граничных условий на гидроупругую устойчивость двух параллельных пластин, взаимодействующих со слоем текущей идеальной жидкости

Пакет параллельных пластин нередко является составным элементом современных инженерных сооружений и находит своё применение в качестве важных компонентов в устройствах АЭС, теплообменников, плавучих морских платформ для добычи нефти и другом. Известно [1], что при взаимодействии упругих тонкостенных пластин с потоком жидкости возникают колебания, вызывающие опасения за целостность включающих их конструкций. Повышенные требования к безопасности наряду с высокими скоростями течения и жёсткими ограничениями по габаритам и массе требуют не только исследования динамического отклика подобных систем, но и определения критической скорости потока, при превышении которой системы теряют устойчивость.

Первые эксперименты в этой области начали проводиться во второй половине XX века и, как правило, на тестовых реакторах [2–5]. Испытываемые образцы представляли собой набор параллельно расположенных пластин, в узких каналах между которыми протекала охлаждающая жидкость.

Наблюдения показали, что при низких скоростях потока пластины деформировались, частично или полностью блокируя канал. Данное явление известно как статическая потеря устойчивости или дивергенция. При высоких скоростях течения возникали самовозбуждающиеся колебания большой амплитуды, которые в конечном итоге приводили к динамической неустойчивости, называемой флаттером.

Исходя из этих результатов автором работы [6] была предложена формула для вычисления критической скорости дивергенции. Аналитическое выражение строилось на основе балочной теории и теоремы Бернулли для несжимаемой жидкости, а также на предположении о равенстве перепада давления между каналами и упругой восстанавливающей силы пластины. В дальнейшем применялись другие критерии, учитывающие эффекты трения жидкости и перераспределения потока [7], нелинейность, вызванную большими прогибами пластин [8, 9]. В [5] выполнено экспериментальное исследование гидроупругой устойчивости трёх модельных топливных сборок, состоящих из параллельных пластин. Установлено, что в конструкциях такого типа возникает несколько видов неустойчивости: дивергенция переднего края пластин, статическая деформация пакета, низкоамплитудные колебания в виде бегущих волн и флаттер. Теоретическое изучение этих особенностей было продолжено автором несколько позднее [10]. При этом пластина считалась бесконечной в двух направлениях и описывалась с помощью уравнений Навье как балка.

Проектирование современных, технологически совершенных и сложных технических изделий из новых конструкционных материалов и сплавов зачастую сопровождается численным моделированием происходящих в них процессов. Проведение наряду с этим натурных экспериментов позволяет на упрощённых макетах не только глубже понимать динамические явления, но и верифицировать предлагаемые теоретические подходы [11, 12]. Соответствующие модели внедрены в коммерческие конечно-элементные пакеты и охватывают довольно широкий класс задач.

В контексте затрагиваемой в данной статье проблемы интерес представляет модальный анализ. Численноаналитический метод для определения собственных частот колебаний двух параллельных прямоугольных пластин, содержащих жидкость между ними, предложен в [13]. Решение построено в виде разложения перемещений упругой конструкции и потенциала скоростей жидкости в конечный ряд Фурье. В [14] оценено влияние величины слоя жидкости и числа пластин на собственные частоты колебаний всей сборки. Отметим, что авторы ограничились изучением только одного варианта кинематических граничных условий.

Нахождение границы гидроупругой устойчивости массива параллельных прямоугольных пластин численными методами представлено в литературе ограниченным числом работ. Трёхмерная постановка задачи предложена в [15, 16]. В обеих работах жидкость описывается уравнениями в терминах потенциала скоростей, полагается, что все пластины, образующие сборку, в произвольный момент времени имеют одинаковые прогиб и форму. При этом любые две, лежащие по соседству, отклоняются в противоположных направлениях. Такое допущение даёт возможность вместо всего набора рассматривать только одну пластину. В [15] перемещения пластины отыскиваются расширенным методом Галёркина, а для вычисления возмущения давления применяется преобразование Фурье. При таком подходе условие непроницаемости приводит к сингулярному интегральному уравнению типа Коши, которое разрешается численно с использованием квадратур Гаусса–Чебышёва. В работе продемонстрировано, что при большом отношении сторон и малой высоте слоя жидкости пластины теряют устойчивость в виде дивергенции по первой моде. Однако для коротких пластин первичная неустойчивость наступает в виде связанного флаттера как результата слияния двух мод колебаний. В отличие от [15], в [16] авторами выяснено влияние на критические скорости потери устойчивости нескольких вариантов кинематических граничных условий, задаваемых на краях как одиночной, так и входящей в сборку пластины. Решение получено с помощью гибридного конечного элемента — элемента, в котором точные функции перемещений определяются непосредственно из уравнений теории оболочек Сандерса. Найденные критические скорости дивергенции хорошо согласуются с данными вычислений по аналитическим формулам, предложенным в [6], особенно при малой высоте слоя жидкости. Однако из-за отсутствия достаточной информации (граничных условий для жидкости, физико-механических параметров рассматриваемой системы, критерия устойчивости) представленные результаты не могут быть воспроизведены. При анализе пластины, помещенной в канал с жёсткими стенками, часто прибегают к теории балок Эйлера–Бернулли [17–19]. Двумерное течение жидкости в этом случае описывается либо уравнениями Навье–Стокса [17], либо с помощью метода вихрей [18, 19]. Устойчивость консольной пластины в вязком воздушном потоке между двумя жёсткими стенками была предметом изучения в [17]. Показано существование двух видов неустойчивости: флаттера и дивергенции. Флаттер возникает при одновременном течении в верхнем и нижнем каналах, а дивергенция — при течении только в одном из них. Несмотря на то, что работа посвящена аэроупругой устойчивости, наличие вязкости допускает применение разработанного конечно-разностного алгоритма в задачах гидроупругости. В [18] показано, что критическая скорость потери устойчивости снижается с увеличением длины пластины и постепенно достигает асимптотического значения.

В настоящей работе, в отличие от цитированных, анализ собственных колебаний и динамической устойчивости упругих параллельных пластин, взаимодействующих с неподвижным или текущим между ними слоем идеальной жидкости, выполнен в трёхмерной постановке. Численная реализация на основе метода конечных элементов позволяет проверить влияние граничных условий разного рода, получить из решения уравнений потенциальной теории распределение гидродинамического давления на упругой поверхности напрямую, без использования допущения о совместности колебаний обеих пластин. Возможности разработанного конечно-элементного алгоритма демонстрируются на примере оценки влияния высоты слоя жидкости на собственные частоты колебаний, вид потери устойчивости и критические скорости течения между параллельными прямоугольными пластинами при разных комбинациях кинематических граничных условий.

2.    Математическая постановка задачи

Рассмотрим две параллельные упругие прямоугольные пластины толщиной h , отстоящие друг от друга на расстоянии H . В образуемом ими канале с жёсткими боковыми стенками со скоростью U течёт

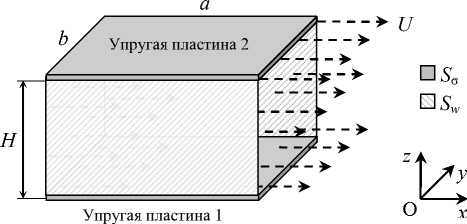
Рис. 1 . Расчётная схема

жидкость. Геометрические параметры модели представлены на рисунке 1. Деформации, возникающие в пластинах в результате гидродинамического воздействия, являются малыми. Влияние пограничного слоя и вязкости жидкости учитывать не будем.

В случае малых возмущений основные уравнения, описывающие динамику идеальной жидкости, занимающей объём V_f , запишем в связанной с пластинами декартовой системе координат O xyz с помощью потенциала возмущённых скоростей ф [20]:

V2q =

±дф+ 2U 8 2 ф + M 2 д 2 ф c ² d t ² c ² д t д x       д x ²

Здесь: t — время; c — скорость звука в жидкости; M = U/c — число Маха.

На границе S _G между жидкостью и упругими пластинами зададим условия равенства нормальных скоростей и нормальных напряжений [21]

W = V ,   G p = G f ,                                           (2)

n , nn nn , где w — нормальная составляющая вектора перемещений пластины; vn — скорость жидкости в направлении внешней нормали к плоскости SG; gpn, gnn — нормальные напряжения в упругой конструкции и жидкости на границе контакта. Для малых перемещений вектор нормали к поверхности SG незначительно отклоняется от координаты z , поэтому в контексте теории пластин граничные условия (2) примут вид raw+и awV^, v at     ax) az дф T.дф

P = -Pf Hr+U^T I.(4)

V dt

Выражение (3) представляет собой условие непроницаемости, а (4) — линеаризованное уравнение Бернулли, где p — гидродинамическое давление, действующее по нормали к поверхности S _G , р f — плотность жидкости.

На границе жидкости и жёсткой стенки S_w зададим условие

Зф/а n = 0.

На входе и на выходе из жёсткого канала рассмотрим два варианта граничных условий для потенциала возмущённых скоростей:

x = 0: ф = 0, x = a : дф/д x = 0;

x = 0 : дф/д x = 0, x = a : дф/д x = 0.

Деформации упругих пластин определим с помощью теории, основанной на гипотезах Тимошенко [22]

^{Е    {}^ xx , ^Е yy , ^Y у , ^Y xz

T du  dv  du  dv  dw  „  dw  „I

—, —, — + —, — + 6 x, — + 6 y Г dx  dy  dy  dx  dxd

T

Y yz } = e + z k ,

T f /50, 50 y 50, 50 y 1

k = 5 —-, —-, —- + —-, 0, 0Г

[ d x    d y    d y    d x

,

где u , v и w — перемещения точек срединной поверхности, соответственно, в направлении осей x , y , z ;

0 _x и 0 _y — углы поворота нормали вокруг осей y и x .

Физические соотношения, связывающие вектор усилий и моментов T и вектор деформаций е , в матричной форме имеют вид

T = { N , N yy , N y , M , M yy , M y , Q x , Q y } T = De .

Для изотропного материала коэффициенты, входящие в матрицу жёсткостей D , находятся известным образом.

Для математической постановки задачи динамики пластин обратимся к вариационному принципу возможных перемещений, который включает уравнение Бернулли (4) и работу сил инерции. В матричной форме он может быть записан для каждой из пластин следующим образом:

J 5 e ^t De dS + J p s 5 d^Td dV - J 5 d ^T P dS , P = { 0 0 p 0 0 } T , S s                    V s                      S „

где p s — плотность пластины; d и P — вектора обобщённых перемещений и поверхностных нагрузок; точкой над символом обозначена производная по времени.

• 3.    Численная реализация

Слабая формулировка конечно-элементной постановки задачи динамики жидкости является результатом применения метода Бубнова–Галёркина к волновому уравнению (1) и граничным условиям (3), (5)–(7). Полученные разрешающие соотношения запишем в матричном виде:

M f f + C c f f + ( K _f + A f ) f - C _f w - A _f w = 0.

Здесь:

M f = ZI1 FT F dV,   Cf = Z f 2U F F dV,   K f = Z J f dF! F+dFT F+dFT F 1 dV, mf J C                     mfVj C   dx                   mf J ( 5x 5x 5y dy dz dz J

d F T d F                                         d N ^w

• A, = -У [ M ²-- dV , C, = У [ FTN dS , A, = У f U F ^T--- dS ; m_f, m_n — число конечных

f                                      , f                         , f                                        f, a mf- Vf      xv xv                  m „ S„                         m „ S„        xA

элементов, на которые разбиваются область жидкости V f и граница S _а ; f — вектор узловых значений потенциала возмущённых скоростей ф ; F , N ^w — функции формы для потенциала возмущённых скоростей и нормальной составляющей w вектора перемещений пластин. Дискретизацию объёма жидкости осуществим с помощью 20-узлового конечного элемента в форме призмы с квадратичной аппроксимацией неизвестных [23].

Вариационное уравнение (10) с учётом (4) после ряда известных конечно-элементных процедур приводится для каждой из пластин к следующему матричному виду:

ее                                 •

M s d + K s d + C s f + A s f = 0.

Здесь: Ms =£jp sNTNdV; Ks =£JBT DBdS ; Cs =£jp f FTN wdS ; As =£jp fU (Nw )T — dS ; ms Vs ms Ss m x S„ m x S „ dx ms — число конечных элементов, на которые разбивается поверхность пластины; N — функции формы конечного элемента; B — матрица связи деформаций с узловыми перемещениями и углами поворота. Дискретизация пластин проводится 8-узловыми КЭ с квадратичной аппроксимацией узловых неизвестных;

на границе с жидкостью используется совместная конечно-элементная сетка.

Таким образом, задача исследования динамического поведения двух упругих параллельных пластин, взаимодействующих с текущей между ними идеальной жидкостью, сводится к совместному решению систем уравнений (11) и (12)

{ •        • •• A T ( *      •    • A T _{z               x z}                   _ т

d 1 f d ₂ } + C { d 1 f d 2 } + ( K + A ){ d 1 f d ₂ } ' = 0,

M = diag { M„ , M f , M , 2 } , K = diag { K, , K f , K , 2 } ,

	" 0	C s 1	0 "		" 0	A s 1	0 1
C =	- C f 1	C c f	- C f 2	, a =	- A f.	A c f	- A f 2
	_ 0	C s 2	0 _		_ 0	A s 2	0

Подстрочными индексами « 1 » или « 2 » обозначена принадлежность переменной к нижней или верхней пластине, а K , M , C , A — соответственно матрицы жёсткости, масс, демпфирования и гидродинамической жёсткости.

Рассмотрим возмущённое движение упругой конструкции и жидкости в виде ( d 1 , f , d ₂ ) = ( d 1 , f , d ₂ ) exp( X t ), где d 1 , f , d ₂ — функции координат, a X = 5 + i to — комплексные собственные значения. Традиционно считается [24], что to — это собственная частота колебаний, а 5 характеризует демпфирующие свойства системы. С учётом этого исходная система уравнений (13) преобразуется в обобщённую задачу на собственные значения для несимметричных матриц удвоенной размерности:

C K + A-I 0

X '

+х

M

0 ]{? } = 0,

где I — единичная матрица, x = { d f } .

Вывод о состоянии системы (13) с точки зрения устойчивости следует из анализа корней

уравнения (14), использовались Арнольди [25]. нарастающими,

полученных при увеличивающейся скорости потока [24]. Для вычисления X процедуры ARPACK, в основе которых лежит неявно перезапускаемый метод Если параметр 5 < 0, то колебания являются затухающими, если же 5 > 0, то — и имеет место динамическая потеря устойчивости в виде флаттера. Дивергенция наблюдается при to = 0 и положительном 5. Скорость, при которой параметр 5 становится положительным, будем называть критической — Ycr.

4.    Численные результаты

Расчёты выполнялись при следующих геометрических размерах и физико-механических характеристиках: a = 0,24 м; b = 0,32 м; h = 2 - 10 ^{- 3} м; H = 0,04 м; E = 69 ГПа; v = 0,3; c = 1500 м/с; p s = 2700 кг/м³; p f = 1000 кг/м³. Для кинематических граничных условий (ГУ), задаваемых на краях пластин, введены следующие обозначения: C — жёсткое закрепление ( u = v = w =9 x =9 y = 0 ) ; F — свободный край. В названии комбинации вид ГУ перечисляется по часовой стрелке, начиная с левого края. Например, вариант CFFF–CFFF соответствует консольным пластинам, закреплённым только на стороне, где втекает жидкость. Для представления результатов используются безразмерное собственное значение Л и безразмерная скорость Y

^Л=^Л Re ⁺ i ^Л Im

a 2 h ^x , ^y= a^DU, ^d =

Eh ³

12 ( 1 -v ² ) .

С целью оценки достоверности решения, полученного с помощью разработанного конечно-элементного алгоритма, сравним его результаты с представленными в [13] данными. В таблице 1 приведены значения вычисленных собственных частот колебаний (Гц) двух жёстко закреплённых (СССС–СССС) параллельных пластин, взаимодействующих с неподвижной жидкостью. Видно, что различие не превышает 5%. Через m и n обозначено количество узловых линий в направлении осей O x и O y .

Таблица 1. Собственные частоты колебаний (Гц) двух параллельных жёстко закреплённых пластин, взаимодействующих с неподвижной жидкостью

m	n	Моды «в противофазе»		Моды «в фазе»
		[13]	МКЭ расчёт	[13]	МКЭ расчёт
0	0	—	—	114,10	113,55
	1	59,4	58,60	194,50	193,25
	2	159,4	155,12	330,90	328,47
	3	287,2	310,62	524,70	520,62
1	0	106,6	104,02	275,40	273,68
	1	170,1	167,87	353,90	350,74
	2	281,3	287,07	488,50	484,08
	3	465,9	465,44	683,80	676,86
2	0	307,8	301,90	533,30	529,93
	1	381,9	390,20	614,70	609,00
	2	494,5	—	751,40	744,91
	3	710,5	725,13	949,90	941,46
3	0	593,4	626,41	898,40	892,53
	1	725,6	726,38	985,10	975,49
	2	890,7	890,12	1127,60	1116,80
	3	1122,5	1118,81	1332,50	1319,88

Ниже представлены результаты, расширяющие имеющиеся в литературе сведения о границе гидроупругой устойчивости параллельных пластин, взаимодействующих с текущей жидкостью. Трёхмерная постановка задачи позволяет рассмотреть такие варианты закрепления, которые невозможно реализовать в численно-аналитических решениях на основе двумерных формулировок или моделей, в которых одна сторона пластины полагается бесконечной в одном из направлений. Отметим, что к обсуждаемым в текущей статье конфигурациям невозможно применить предложенную в работе [6] аналитическую формулу для вычисления критической скорости дивергенции. Сопоставление с данными из [15, 16] также не представляется возможным по причине отсутствия в этих статьях необходимых примеров.

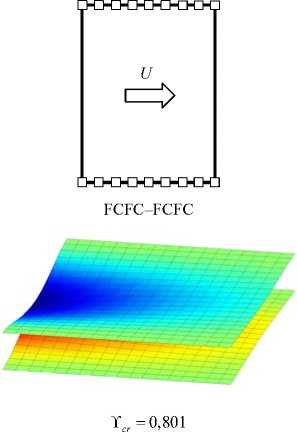
На рисунке 2 приведены формы колебаний упругой конструкции для нескольких вариантов граничных условий, построенные при критической скорости течения Y = Y cr . Здесь обе пластины закреплялись одинаково, а для жидкости использовались ГУ вида (6). Результаты дают основание сделать вывод о том, что квазистатическая потеря устойчивости (дивергенция) наступает по моде «в противофазе», в то время как динамическая (флаттер) — по моде «в фазе». При этом величина критической скорости флаттера на порядок выше скорости дивергенции. Анализ собственных значений для конфигураций вида CCFC–CCFC и CFFF–CFFF показывает наличие явно выраженного демпфирования, которое приводит к стабилизации системы и, как следствие, повышению критических скоростей.

Влияние высоты слоя жидкости продемонстрировано на рисунке 3. Предполагается, что несущая способность нижней пластины такова, что воздействие массовых сил жидкости можно не принимать во внимание. Из представленных данных видно, что зависимость низшей собственной частоты колебаний ю от отношения высоты слоя жидкости H к длине пластин b носит немонотонный характер с явно выраженным экстремумом (Рис. 3 а ). При этом положение точки максимума для каждого из участвующих в расчётах вариантов граничных условий определяется конкретным значением Hb . Результаты свидетельствуют, что низшая собственная частота колебаний возрастает с увеличением числа ограничений, задаваемых на краях. Несколько иное поведение имеет место в случае текущей жидкости (Рис. 3 б ). Проведённые расчёты показали, что для консольных пластин (CFFF) потеря устойчивости осуществляется в виде флаттера по первой балочной моде при H/b <  0,08 и по второй — при H/b >  0,08 . Смена режима колебаний сопровождается скачкообразным ростом критической скорости. Аналогичная особенность наблюдается также и при варианте закрепления CCFC. Здесь имеется широкий диапазон линейных размеров, в пределах которых критические скорости снижаются более чем на 15%, а потом резко увеличиваются. В случае дивергенции (см. кривые СССС и FCFC) величина Y монотонно растёт на всём рассмотренном интервале отношения Hb . Отметим, что для всех представленных вариантов закрепления характерна общая закономерность, заключающаяся в том, что критические скорости потери устойчивости изменяются несущественно, если отношение H/b >  0,50. Вышеперечисленные особенности следует принимать во внимание при проектировании реальных индустриальных приложений.

CFCF–CFCF

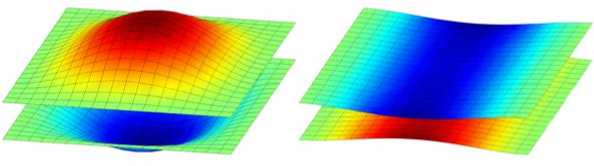
Y cr = 1,374                                Y cr = 0,949

Дивергенция

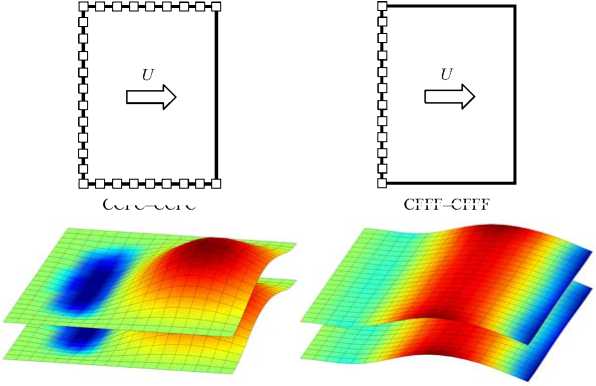
CCFC–CCFC

CFFF–CFFF

Y cr = 9,020

Y cr = 8,232

Флаттер по одной моде

Рис. 2 . Формы колебаний пластин, полученные при разных граничных условиях и Y = Y cr

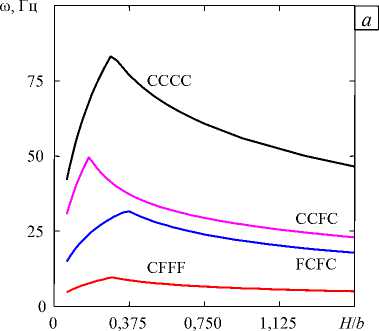
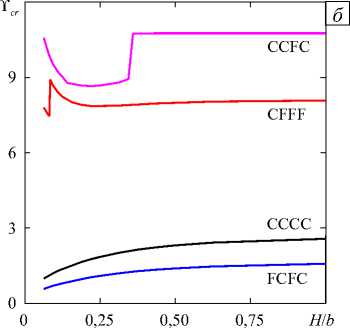
Рис. 3 . Низшие собственные частоты колебаний ( а ) и безразмерные критические скорости потери устойчивости Y cr ( б) двух параллельных пластин при одинаковых граничных условиях

Таблица 2. Безразмерные критические скорости потери устойчивости Y cr двух параллельных пластин при разных комбинациях граничных условий для жидкости и пластин

ГУ для пластин	ГУ для жидкости (6)				ГУ для жидкости (7)
1-я 2-я	CCCC	CCFC	FCFC	CFFF	CCCC	CCFC	FCFC	CFFF
CCCC	1,374	—	—	—	2,906	—	—	—
CCFC	4,285	9,020 *	—	—	3,177	3,433	—	—
FCFC	1,092	1,440	0,801	—	2,226**	Система неустойчива	1,158**	—
CFFF	4,066	8,942 *	1,590	8,232*	3,039	8,200*	Система неустойчива	8,113*

При изучении поведения технических конструкций, включающих параллельные пластины, важным является не только моделирование штатного режима эксплуатации, но и анализ аварийных ситуаций. В качестве примера можно рассмотреть случай, когда нарушается закрепление какой-либо из сторон одной из пластин. Возникающие при этом несимметричные граничные условия приводят к появлению пространственных форм колебаний, и, следовательно, исследование в рамках двумерных постановок не представляется возможным. Трёхмерная формулировка и численная реализация, предложенные в данной статье, позволяют устранить этот недостаток. Полученные при разных комбинациях граничных условий для жидкости и пластин критические скорости приведены в таблице 2. Здесь звёздочкой обозначены флаттер по одной (*) или двум (**) модам колебаний, а остальные значения соответствуют дивергенции.

В первой группе примеров для жидкости используются граничные условия вида (6). Этот вариант достаточно хорошо зарекомендовал себя на практике при оценке гидро- и аэроупругой устойчивости цилиндрических оболочек вращения [26]. Он дает возможность описать качественно поведение систем, наблюдаемое в ходе эксперимента. Из таблицы 2 следует, что динамическая потеря устойчивости в виде флаттера по одной моде имеет место только в тех случаях, когда края обеих пластин закреплены на входе потока в сборку ( x = 0) и свободны на его выходе ( x = a ). При остальных видах условий на границе возникает неустойчивость дивергентного типа, причём при значительно меньших скоростях течения.

Совершенно другая картина наблюдается при граничных условиях (7). Несмотря на то, что критические скорости флаттера по одной моде незначительно снижаются (максимум на 10%), для дивергенции однозначную зависимость выявить не удаётся. Более того, закрепление вида FCFC теперь приводит не к квазистатической потере устойчивости, а к флаттеру по двум модам колебаний или к появлению систем, неустойчивых при произвольно малых скоростях течения жидкости. Подобное явление было обнаружено ранее для цилиндрических оболочек с несимметричным закреплением [27]. Следует отметить также, что результаты, полученные при граничных условиях для жидкости вида (7), вызывают сомнение, поскольку в известных экспериментах закреплённый вдоль потока набор пластин теряет устойчивость в виде дивергенции. В связи с этим наиболее физически обоснованной выглядит комбинация граничных условий (6). Именно этот вариант и был использован во всех рассмотренных в данной статье численных примерах, где комбинация граничных условий не оговаривалась особо.

5.    Заключение

В работе представлена трёхмерная постановка задачи исследования собственных колебаний и гидроупругой устойчивости двух параллельных прямоугольных пластин, взаимодействующих с текущей между ними жидкостью, и конечно-элементный алгоритм её численной реализации. По результатам вычислительных экспериментов оценено влияние расстояния между пластинами на собственные частоты колебаний и критические скорости течения при разных комбинациях кинематических граничных условий. Установлено, что в случае неподвижной жидкости низшая собственная частота колебаний конструкции сначала растёт, а затем постепенно падает с увеличением высоты слоя жидкости. У текущей же жидкости характер изменения критических скоростей определяется типом потери устойчивости. При дивергенции скорости монотонно увеличиваются с утолщением слоя жидкости, а при флаттере имеет место их скачкообразное изменение, обусловленное сменой формы колебаний, по которой осуществляется потеря устойчивости. При этом для любого вида неустойчивости рост критических скоростей незначителен, если отношение Hb превышает значение 0,50. На основании анализа состояния системы для комбинаций кинематических граничных условий, задаваемых на краях пластин, показано существование различных видов неустойчивости. Выявлены варианты закрепления, приводящие к возникновению одномодового флаттера.

Работа выполнена при финансовой поддержке РФФИ (проект № 15-01-05254-а) и Совета по грантам Президента РФ для молодых российских учёных (грант МК-6167.2015.1).