Численное исследование вынужденных колебаний жидкой капли на вибрирующей подложке

В последнее время повышенный исследовательский интерес наблюдается в отношении системы «капля на подложке». Эта система эффективна в медицинской диагностике, проводящейся по структуре следа, оставленного после испарения капли биологической жидкости (например, сыворотки крови) [1]. Выявлена принципиально новая возможность использования системы «микрокапля на подложке» в качестве микрореактора для реализации процесса самосборки наноструктур в процессе испарения на подложке коллоидной капли с наночастицами [2]. Остаются актуальными технологические приложения явления: в струйной печати, для охлаждения твердых поверхностей испарением помещенных на них капель, в технологиях нанесения жидких защитных покрытий. В сравнительно недавних работах изучается падение капли на жидкую пленку [3] и твердую поверхность [4], отскок капли воды от гидрофобной поверхности [5].

Кроме того, исследования вынужденных и свободных колебаний лежащей капли имеют фундаментальное значение, в частности потому, что включают два важных аспекта: поведение свободной поверхности жидкости и области трехфазного контакта. Так, в [6, 7] проведен численный анализ нелинейных вынужденных колебаний висящей капли и обнаружен гистерезис контактного угла. В [8] проведено аналитическое решение задачи о капле идеальной жидкости на вибрирующей подложке, когда условия на трехфазной границе описываются формулами Хокинга [9]. Скорость движения линии раздела в этом случае предполагается пропорциональной отклонению контактного угла от равновесного. В [8] показано, что такие условия вызывают появление трения на трехфазной границе и приводят к энергетическим потерям даже для колебаний идеальной жидкости. Капля на вибрирующей подложке подробно исследована экспериментально, например, в [10], в обоих крайних случаях постоянного краевого угла и закрепленной границы раздела. Авторы наблюдали формирование стоячих гравитационно-капиллярных волн, измерили их собственные частоты и зафиксировали положения узлов и пучностей. Результаты были интерпретированы в рамках теории одномерного осциллятора.

Однако за границами исследованной области остаются следующие вопросы: какова фазовочастотная характеристика объекта «капля-подложка», как на фазу колебаний влияют поверхностное натяжение, межфазное натяжение, плотность и вязкость жидкости? Кроме того, все известные авторам численные исследования колебаний капли на подложке проведены для невязких жидкостей в отсутствие силы тяжести и для случая постоянного радиуса пятна смачивания.

Цель настоящей работы состоит в разработке программного пакета, способного описать поведение капли вязкой жидкости на плоской горизонтальной поверхности, вибрирующей с малой амплитудой (случай линейных колебаний) в присутствии поля тяжести и с учетом эффектов, связанных с межфазным натяжением.

1.    Математическая модель

В работе рассмотрена лежащая капля, помещенная на плоскую горизонтальную подложку (рис. 1). Подложка осциллирует в направлении своей нормали с частотой со и малой амплитудой А , так что ее положение в лабораторной СО описывается как z s ( t ) = A sin о . Приняты следующие обозначения: р - плотность жидкости, v - кинематическая вязкость, ^ lg , _gs, C 7 _ls - коэффициенты межфазного натяжения на границах жидкость-газ, газ-твердое, жид-кость-твердое соответственно. Индексами l, g и s обозначены жидкая, газовая и твердая среды.

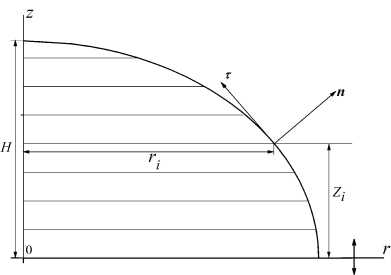
Рис. 1. Лежащая капля располагается на вибрирующей горизонтальной подложке. Показана половина осевого сечения капли

1.1.    Приближения модели

Мы предполагаем верными следующие предположения о состоянии капли и течениях в ней:

• •    жидкость является ньютоновской и несжимаемой; практически это означает, что выполнено условие COR <<  c , где c - скорость звука в жидкости, R - радиус равновеликой сферической капли;

• •    влияние газа пренебрежимо мало;

• •    пренебрегаем испарением с поверхности капли, т.е. нет необходимости рассматривать смещение границы, связанное с потерей массы;

• •    форма капли имеет осевую симметрию, как и поля скорости и давления в ней;

• •    можно пренебречь тепловыделением внутри капли, так что жидкость можно считать изотермической.

1.2.    Система уравнений сохранения и граничные условия

Введем систему координат с осями, в которой подложка неподвижна (см. рис. 1), V = {Vr, Vz} - вектор скорости, p есть превышение давления над гидростатическим P0, т.е. p = P - P0, где P0 - гидростатическое давление в равновесной капле, определяемое формулой P0 (z) = -оlg - K0 (z), K0 (z) - кривизна равновесной капли.

Тогда уравнения сохранения вещества и импульса в неинерциальной системе отсчета запишутся в виде ———► д V     —— —— ——       1 ——       —— — А

---+ (V-v) V =--Vp + vV 2V +—sin ot,                      (1) д t v ' pO'

V - V = 0.(2)

Условия на границе жидкость-газ S _lg запишутся как:

"T"Slg = ^K •(3)

" '^1 S, = 0,(4)

здесь Т у =- P S y + n ( d u i /Э X j +d U j^ x i ) - тензор напряжений, A = { 0,0, A } , П = vp - динамическая вязкость. Уравнение (3) представляет собой формулу Лапласа, а (4) означает, что касательные напряжения отсутствуют. В (3) и (4) граница «жидкость-газ» предполагается бесконечно тонкой и невесомой.

Граничные условия на твердой подложке запишутся как:

V '^s = ⁰, ^s = ⁰-                                  ⁽⁵⁾

Динамика поведения контактной линии описана в работе следующими способами 1) r 1 = const - постоянный радиус пятна смачивания, 2) 6 = 6 0 = const - постоянный (равновесный) контактный угол.

Физика

Здесь r - радиус пятна смачивания, 0 0 - равновесный контактный угол.

Уравнения приведены к безразмерной форме так, что все линейные размеры отнесены к радиусу R , скорости - к U o = A to , напряжения - к р и 2 и время - к Ru 0 . Характерные значения параметров жидкости и материала подложки и безразмерных критериев задачи приведены в таблице 1 и обсуждены в секции 3.

1.3.    Начальные условия

Предположим, что при t <  0 капля находилась в состоянии статического равновесия и в момент t = 0 подложка начала вибрировать: ^^

t = 0: p = о, 5 ig = 5 о , V = 0, где 5 ₀ - есть равновесная форма поверхности капли.

2.    Численные методы

Численное решение проводилось методом конечных разностей, где использовалась неравномерная сетка. Сначала капля делилась на m равных по толщине горизонтальных слоев. Форма

Таблица 1

Значения парамет ров расчета и безразмерных характеристик Радиус равновеликой сферической капли R, м 10-3 Кинематическая вязкость v , м2с 1 10-6 Амплитуда колебаний подожки A, м 10-4 Частота колебаний подложки to, с-1 400–3500 Плотность жидкости р, кгм 3 1000 uL Число Рейнольдса Re = -0— v 4 – 35 Поверхностное натяжение    olg, [|V 0,073 _ ogR2 Число Бонда Bo = —--- oig 0,14 Разность межфазных натяжений °ls - ogs , №м-1 0 _        ou2 R Число Вебера We= —0— oig 10-4 -10-2 Номер моды колебаний l 2, 3, 4 капли описывалась массивами {r, i = 1, m} и {z;, i = 2, m+1} (рис. 1). Очевидно, что rm+i = 0 и Zi = 0. Затем производилось деление вертикальными линиями, при этом необходимо соблюдение условия, чтобы ширины прямоугольных ячеек разбиения не отличались более чем на 30 %, это необходимо для сходимости расчета. Уравнения (1)-(6) записывались в разностной форме. Полученная система алгебраических уравнений решалась методом Гаусса. Решение проводилось в духе метода расщепления и делилось на следующие стадии:

• •    давление и скорости в капле находятся решением (1)-(5). Форма капли считалась неизменной на этой стадии;

• •    определяется новая форма капли по формулам:

r t ^+А t = r t + V r    • Д t , i = 2, m , z t ^+A t = z t + V_z    -A t , i = 2, m + 1.

S lg                                                 S lg

Радиус пятна смачивания определяется из условий (6) по формулам

• 1)    r 1 = const; t +А    t +А

• 2)    r    = r 2    ^{+ z} 2 • ctg 6 0 ;

• • сетка перестраивается в соответствии с новой формой капли.

3.    Обсуждение результатов

Расчеты проводились для различных пространственных разбиений и временных шагов, и было получено независящее от параметров сетки решение. Алгоритм был протестирован сравнением с известным аналитическим решением [11, 12]. Программы для расчета были написаны на языке Фортран и распараллелены с использованием библиотеки MPI. Вычисления проводились на суперкомпьютере ТОРНАДО (ЮУрГУ).

Значения физических параметров, использованных при решении задачи, и соответствующих безразмерных критериев указаны в табл. 1. Как видно из таблицы, амплитуда колебаний подложки мала, так что ожидается только линейный отклик системы. Число Рейнольдса также мало, следовательно, в капле возникают лишь ламинарные течения. Значения числа Вебера указывают на то, что при колебаниях не будет разбрызгивания. Значения числа Бонда показывают, что и гравитационная, и поверхностная силы будут влиять на течения в капле и ее форму.

На рис. 2 приведены амплитудно-частотные характеристики вынужденных колебаний капли для случаев постоянного контактного угла и закрепленной линии контакта. Обе кривые представляют собой зависимости безразмерной амплитуды колебаний капли в вершине от частоты вибраций подложки. Как показало сравнение с результатами работы [13], абсциссы пиков на графиках совпадают с собственными частотами капли для соответствующих мод колебаний.

Резонансные частоты колебаний с постоянным контактным углом (I) получились меньшими, чем для колебаний с закрепленной линией контакта (II). В [10] такой сдвиг частот был исследо ван экспериментально, и для его описания была предложена формула у/у =(2/ —1)/(2/ — 2),

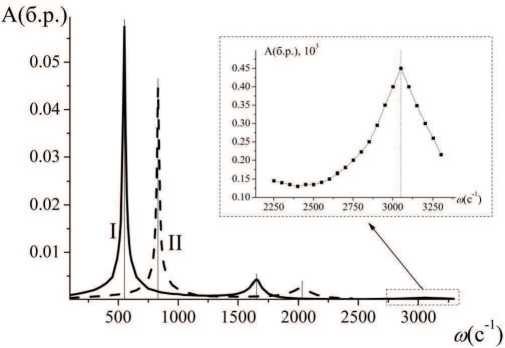
Рис. 2. Амплитудно-частотая характеристика вынужденных колебаний капли; I - постоянный контактный угол, II - закрепленная линия трехфазного контакта

Таблица 2

Отношение У ц/ у для мод колебаний

Номер моды	/ = 2	/ = 3
Эксперимент [10]	1,5	1,25
Расчет [эта работа]	1,509	1,237

где у и у - есть резонансные частоты в случае свободно движущейся и закрепленной границы трехфазного контакта, / - номер моды. Номера мод колебаний капли совпадают с индексами полиномов Лежандра, которые были получены Рэлеем при решении задачи о колебаниях свободной капли в [12]. В табл. 2 представлены численные значения у \у. Как видно из таблицы, численные и экспериментальные значения близки между собой, что указывает на хорошую точность расчетной схемы.

На рис. 3 показаны мгновенные поля скоростей в осевом сечении капли, полученные при резонансе для трех мод с постоянным контактным углом. Длины векторов на рисунке масштабированы так, что относятся как 15:5:1. Как видно из рисунка, на поверхности капли существуют узлы - точки, находящиеся в покое при колебаниях (на рисунке отмечены жирным). Рассчитанные положения узлов качественно совпадают с экспериментальными, полученными в [10].

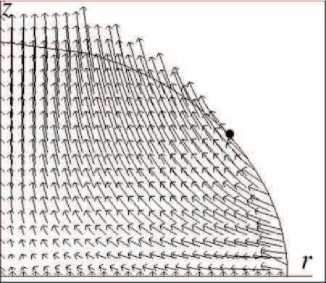
a ) / = 2

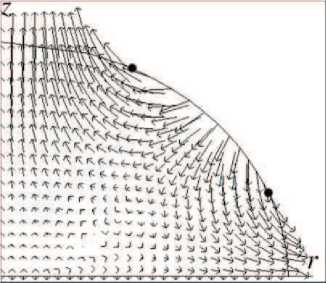
b ) / = 3

Рис. 3. Мгновенное поле скоростей для низших мод с постоянным контактным углом. Показана половина осевого сечения капли

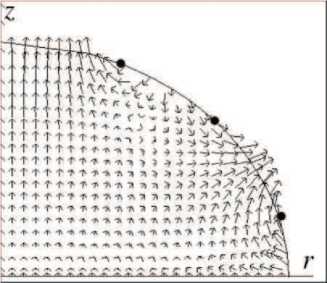
c ) / = 4

Физика

4.    Выводы

В работе проведено исследование поведения лежащей капли на вибрирующей подложке с учетом гравитации, вязкости и условий на трехфазной границе. Получены амплитудно-частотные характеристики колебаний вершины капли на подложке для режимов с постоянным контактным углом и закрепленной трехфазной границей. Резонансные частоты совпадают с собственными частотами колебаний капли для всех изученных мод колебаний. Наблюдалось формирование в капле стоячих капиллярных волн, расположение узлов и пучностей которых качественно совпадает с экспериментальными данными, найденными в литературе.

Проведенные расчеты и сравнения позволяют сделать вывод о возможности использования разработанных программ для количественного исследования характеристик системы «капля-подложка» при различных значениях физико-химических параметров жидкости и материала подложки.

Авторы благодарят проф. В.П. Бескачко за полезное обсуждения и внимание к работе.