Численное исследование взаимодействия сооружений с грунтовым основанием при сейсмических воздействиях

Изучение динамического контактного взаимодействия сооружения с грунтовым основанием является важным элементом исследования сейсмопрочности как примыкающих подземных элементов, так и сооружения в целом. В [1] предложен приближенный метод, в котором жесткость основания учитывается путем введения совокупности упругих связей, присоединенных к фундаментной плите. Однако динамическая жесткость основания зависит от его размеров, величины нагрузки, типа грунта и так далее, поэтому определение используемых в [1] параметров до сих пор остается недостаточно изученной проблемой. Наиболее полно особенности контактного взаимодействия сооружения с основанием учитываются в случае, когда воздействие в расчете задается акселерограммой землетрясения, зарегистрированного в сейсмогеологических и грунтовых условиях, близких к условиям площадки строительства проектируемого сооружения. Подобные исследования, сопряженные с численным решением трехмерных задач динамики, из-за большой размерности расчетной области чрезвычайно трудоемки даже для современных высокопроизводительных вычислительных систем. В [2] изложен метод решения двумерных задач сейсмостойкости сооружений, который существенно сокращает вычислительные затраты, учитывает эффекты контактного взаимодействия с грунтовым основанием и дает результаты, удовлетворительно согласующиеся с экспериментальными данными.

Поскольку давление в грунте при прохождении сейсмических волн 8-балльной магнитуды не превышает 0,05 МПа, грунт считается идеально упругой средой. Расчетная область находится в поле силы тяжести. Численное моделирование задач осуществляется в двумерной постановке. Движение среды описывается в переменных Лагранжа в декартовой системе координат O xz . Кинематические соотношения формулируются в скоростях и строятся в метрике текущего состояния, что позволяет учитывать большие перемещения и формоизменения свободных и контактных поверхностей. Связь между компонентами тензоров скоростей напряжений и скоростей деформаций подчиняется обобщенному закону Гука. Из вариационного принципа Даламбера–Лагранжа в форме Журдена следует вариационное уравнение:

JJ ( ⁿ ( 5 й_и + § u j , i )/ 2 + P u_lSU_l + P g£u i ) d П - J p i S udS - J q i Su i i dS = 0.                  (1)

n                                               G           G

Здесь G y — компоненты тензора напряжений Коши; и i — скорости перемещений; p i , q i — компоненты поверхностной нагрузки и контактного давления ( i = x , z ). Для определения в (1) компонент контактных усилий q i в местном координатном базисе 5 , £ , связанном с поверхностью контакта ( 5 , £ — направления касательной и нормали к поверхности), усилие по нормали находится из условия непроникания:

.V .\” и ^ = и ^ , q ' = - q ' ,

, I 0,    q. > 0, q^ = qП q,,  £< 0;

касательное усилие определяется на первом этапе из условия жесткой склейки, а в случае превышения силы трения покоя — в соответствии с законом Кулона:

(и 5 = и ‘ { q = - q

/ q , kl ^ k ^ q ?| ,

q = q =

1 k ^ q sign ( q_s ) , q s l >  k § q § I-

Здесь к ^ — коэффициент трения. Связь контактирующих подобластей полагается односторонней, то есть допускается их отрыв друг от друга и повторное вступление в контакт, поэтому условия (2), (3) применяются только при действии сжимающих усилий.

Решение определяющей системы уравнений при заданных начальных и граничных условиях основывается на вариационно-разностном методе дискретизации по пространственным координатам и явной схеме интегрирования по времени. Замена интегрирования по области Q суммированием по ячейкам разностной сетки приводит к дискретному аналогу уравнений движения каждого узла сетки [3]:

( Mu i ) j = ( F ) .

Здесь F_i — обобщенные силы, действующие на расчетный узел j ; M — масса в j -м узле.

Процесс деформирования сплошной среды во времени разбивается на временные слои t ⁰, t ¹, ..., t^k , ... с шагами A t^{k + 1} = t^{k + 1} - t^k . Схема интегрирования уравнений (4) по времени представляется в виде:

/ . \k +1/2     / . \к -1/2    / т-, \ к . ^+1/2 // 1 k\k         ( k ^{+ +1}     /    \^k / • \^{k +1/2}_A ,^+l

( u t i j y = ( ^U i ) y ⁺( F \ ^At t ⁺ J ( ^M ) y ,      ⁽ U), =^{( U} i ) _y + ( ^U }j ^A t

A t ^{k +1/2} = ( A t ^{k +1} +A t ^k ) /2,     ( i = x , У ) -

Здесь выбор шага интегрирования по времени A t^{k +1} осуществляется исходя из условия устойчивости Куранта [3]. Разностная схема (5) является схемой второго порядка точности, и на разрывах напряжений и скоростей перемещений приводит к значительным осцилляциям численного решения в среде. При этом для подавления нефизических осцилляций применяется процедура консервативного сглаживания. Описанный метод решения, алгоритмы моделирования контакта и поля силы тяжести реализованы в программном комплексе «Динамика-2» [4].

Экспериментальные и синтезированные акселерограммы определяют кинематические характеристики в одной точке поверхности грунта, а для численного решения задачи необходимо иметь кинематические или силовые граничные условия, при задании которых на границе расчетной области вблизи сооружения воспроизводилась бы известная акселерограмма. Задача нахождения импульсной нагрузки является некорректной из-за неопределенности расположения источника землетрясения и, как следствие, неопределенности волнового вектора скорости сейсмических волн относительно поверхности. Поскольку сооружение располагается вблизи поверхности и его размеры по сравнению с длинами сейсмических волн малы, приходящие от источника землетрясения к сооружению волны можно считать плоскими и распространяющимися по нормали к дневной поверхности грунта. При сделанных допущениях отсутствие информации об источнике сейсмического воздействия не повлияет на результаты расчета, если приходящие к поверхности грунта сейсмические волны воспроизводят экспериментальную сейсмограмму с заданной точностью.

В соответствии с предлагаемой численной методикой сейсмограмма на поверхности грунта представляется в виде кусочно-линейной функции:

C i ( t h ) = £ aH ( t h - 1^ ,                                        (6)

где a i — приращение к амплитуде сейсмограммы в данной характерной точке; H ( t h - t i ) — функция Хевисайда; t h — дискретные значения времени, отвечающие характерным точкам сейсмограммы на поверхности ; t_t — сдвиг по времени характерной точки сейсмограммы.

Далее сеточно-характеристическим методом решается одномерная задача распространения в грунтовой среде волны, заданной на границе в виде функции Хевисайда. Зная, как изменилась тарировочная функция при пробеге через грунтовый массив, по экспериментальной сейсмограмме C 1 в каждой опорной точке можно восстановить искомую сейсмограмму на нижней границе области грунта C ₀:

с 0 ( t h ) = [ C ( t h + 1 *) H 0 ( t h ) ]/[ H 1 ( t h + 1 *) ] , (7)

где H ₀ — тарировочная функция; H 1 — сейсмограмма на поверхности, полученная из решения задачи; t * — время пробега волны от нижней границы грунтового массива до его поверхности. Линейная интерполяция по полученным из (7) опорным точкам позволяет найти сейсмограмму на нижней границе грунтового массива отдельно для сдвиговых и продольных волн. Данная методика может быть применена и для п- слойного грунта. Шаг разностной сетки обуславливается точностью описания высокочастотных осцилляций, присутствующих в сейсмограмме. Чтобы дисперсионные эффекты численного решения по явной схеме «крест» не искажали заданную кусочно-линейной функцией волну, необходимо брать число Куранта равным единице. Тогда схема «крест» даст те же результаты, что и сеточно-характеристический метод на равномерной сетке, и дисперсия численного решения не возникнет. Анализ результатов тестирования описанной методики показал, что ошибка в восстановлении сейсмограммы не превышает 1%.

Поскольку при решении двумерной задачи исследования сейсмических колебаний сооружения размеры расчетной области грунта существенно ограничиваются возможностями вычислительной техники, необходимо свести к минимуму погрешности, связанные с краевыми эффектами. Минимизация отражений волн от боковых границ грунтового массива возможна при использовании квазиравномерных сеток [5]. Однако неравномерность сетки порождает нефизические осцилляции и требует сглаживания численного решения. Это снижает эффективность применения таких сеток [5], так как вносит искажение в волны нагрузки, если их источник находится на границе, имитирующей бесконечность. Авторами предложен альтернативный метод корректировки скоростей перемещений, позволяющий сохранить форму одномерных волн сдвига и сжатия, распространяющихся по массиву грунта вдоль граничной поверхности. При выделении, в соответствии с данным алгоритмом, из полупространства примыкающей к сооружению конечной расчетной области на ее боковых границах осуществляется перенос скоростей перемещений из приграничных узлов сетки в граничные.

Для оценки эффективности предложенного способа моделирования граничных условий и сопоставления его с методом квазиравномерных сеток проведено численное решение ряда двумерных задач, в которых исследовалось распространение плоской поперечной волны в упругой прямоугольной области [6]. Рассматривались варианты квазиравномерных сеток, разрежающихся по линейному и гиперболическому законам, и было установлено, что при переносе скоростей на боковых поверхностях из приграничных узлов в граничные решение со временем не искажается, в то время как применение квазиравномерных сеток приводит к постепенному искажению решения за счет отражений от боковых границ.

Для обоснования выбора размеров расчетной области при численном решении задачи необходимо оценить влияние краевых эффектов на решение вблизи сооружения. С этой целью был проведен ряд вычислительных экспериментов [6], анализирующих сейсмические вибрации сооружения с учетом контактного взаимодействия с грунтом. Установлено, что вклад отраженных от сооружения волн становится несущественным, если расстояние от него до границ расчетной области превышает 10 габаритных размеров его основания.

Разработанная вычислительная модель динамического взаимодействия сооружения с грунтом была применена для анализа поведения при сейсмических вибрациях построек АЭС «Бушер» (Исламская Республика Иран), Калининской, Нововоронежской и Ростовской АЭС (Россия). В соответствии с проектами в грунт заложена система трубопроводов, входящих в исследуемые объекты. Для оценки прочности трубопроводов важно определить пиковые амплитуды смещения стен построек относительно грунта. Ниже приведены результаты одного из таких расчетов.

Вид расчетной области представлен на рисунке 1. Требовалось оценить взаимные смещения стенок здания и грунта при 7-балльном землетрясении длительностью 7 секунд. Расчетная область грунта и здания покрывались равномерной разностной сеткой с шагом 1 м. При этом высота ячеек сетки для грунтового массива соответствовала размерам сетки при численным решении одномерной задачи восстановления сейсмической нагрузки. Всего использовалось 447485 ячеек. Контроль достаточности числа сеточных узлов осуществлялся путем сравнения экспериментальной сейсмограммы поверхности грунта с сейсмограммой, полученной при численном решении одномерной задачи. В каждой точке на нижней границе грунта задавались компоненты скорости i t x , i z , восстановленные по изложенной выше

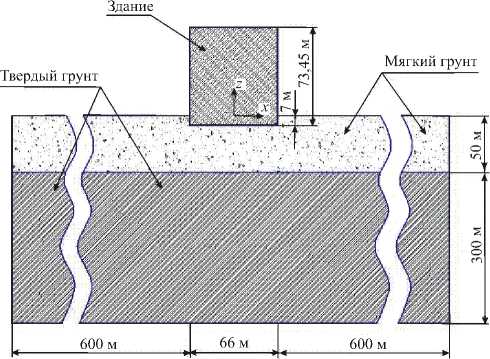
Рис. 1. Вид расчетной области

численной методике из экспериментальной сейсмограммы, зарегистрированной на поверхности полупространства.

Контактное взаимодействие грунтового массива и здания моделировалось условиями непроникания с учетом сухого трения, при этом допускался отрыв стенок здания от грунтового массива. Коэффициент трения между грунтом и зданием составлял 0,2. Начальное поле перемещений системы грунт–здание под действием силы тяжести определялось методом стационирования с введением линейной вязкости [7]. Поведение материалов всех объектов считалось упругим. Механические характеристики были следующими: мягкий грунт — модуль Юнга E = 21 МПа , коэффициент Пуассона v = 0,37, плотность р = 1850 кг/м³; твердый грунт —

E = 2100МПа , v = 0,37 , р = 1850кг/м³; здание — E = 21МПа , v = 0,25 , р = 808кг/м³.

В результате расчета были установлены временные зависимости относительных горизонтальных и вертикальных смещений боковых стенок сооружений и грунта. Рассматривались взаимные смещения контактирующих поверхностей в точках, находящихся на глубине приблизительно 2 м. Поскольку разностные сетки для здания и прилегающего грунта не совпадали, сравнивались смещения ближайших узлов на линии их контакта. Пиковые амплитуды смещения стенок сооружения и грунта составили 2,124 мм в вертикальном и 0,053 мм в горизонтальном направлении. Относительные горизонтальные и вертикальные смещения боковых стенок здания и грунта представлены на рисунке 2.

Проводился анализ факторов, влияющих на поведение сооружений при сейсмических вибрациях. Рассматривались сейсмические вибрации сооружений с учетом контактного взаимодействия с грунтом при различных значениях геометрических и физических параметров: массивности и эксцентриситета центра масс сооружения, величины заглубления фундамента, коэффициента трения на поверхности контакта сооружения и грунта, интенсивности сейсмического воздействия, многослойности грунтового основания. Зависимость вертикальных и горизонтальных смещений от массы сооружения и величины заглубления фундамента представлена на рисунке 3. Из рисунка видно, что массивность сооружения оказывает влияние лишь на вертикальные взаимные смещения стенок сооружения и грунта. С увеличением заглубления от 25% до 100% от высоты здания вертикальные смещения соответственно уменьшаются в 3 раза, а горизонтальные — в 6 раз.

Исследование взаимодействия сооружения с грунтом в зависимости от величины эксцентриситета центра масс проведено для сооружений, заглубленных на 15% и 25% высоты. Сооружение представлялось системой двух блоков, соединенных по оси симметрии здания и имеющих разную плотность: р2 = кэр1, р1 + р2 = const; здесь коэффициент кэ связан с безразмерным эксцентриситетом e формулой e = eL = (1 - кэ )/[4(1 + кэ)], где e — эксцентриситет (расстояние от центра симметрии до центра масс конструкции), L — длина основания. Зависимость взаимных вертикальных и горизонтальных смещений стенок здания и грунта от значения безразмерного эксцентриситета для граничных точек, находящихся на глубине приблизительно 3 м, демонстрирует рисунок 4, зависимости абсолютных вертикальных и горизонтальных смещений — рисунок 5. Из анализа графиков установлено, что эксцентриситет центра

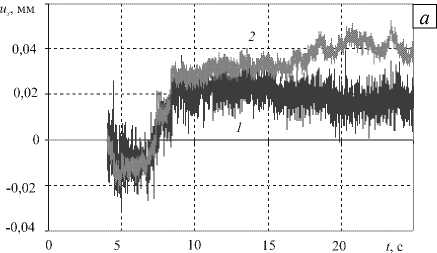
Рис. 2. Относительные горизонтальные ( а ) и вертикальные ( б ) смещения стенок здания и грунта с левой (кривая 1 ) и правой ( 2 ) сторон здания

И., мм 2,0

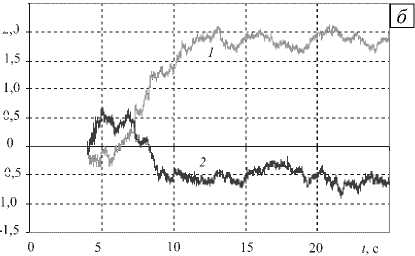
0,5

-0,5

масс при сейсмическом воздействии влияет на раскачивание конструкции в целом в большей мере, чем на взаимные смещения боковых стенок сооружения и прилегающего грунта.

Взаимодействие сооружения с грунтом в зависимости от коэффициента трения на контактных поверхностях показано на рисунке 6. Из анализа графиков вертикальных и горизонтальных взаимных смещений здания и грунта следует, что коэффициент трения оказывает существенное влияние лишь

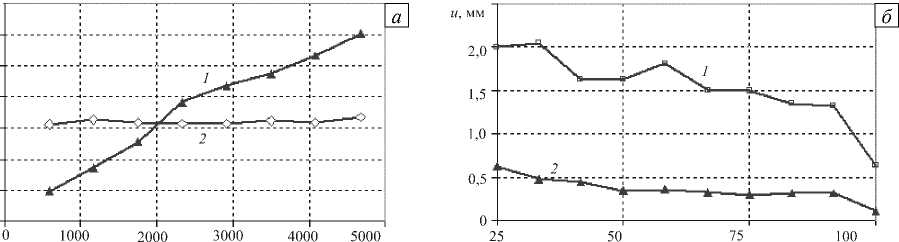
Масса сооружения, т

Заглубление, %

Рис. 3. Зависимость вертикальных U z (кривая 1 ) и горизонтальных U x ( 2 ) смещений от массы сооружения ( а ) и величины заглубления фундамента ( б )

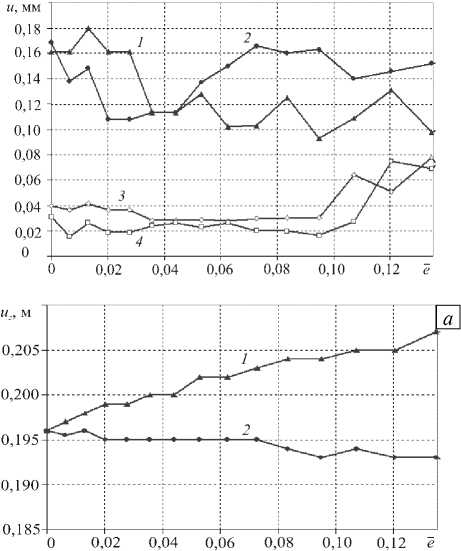
Рис. 4. Взаимные вертикальные U z (кривые 1 , 2 ) и горизонтальные и ( 3 , 4 ) смещения стенок здания и грунта в зависимости от безразмерного эксцентриситета e ; смещения с левой (кривые 1 , 3 ) и правой ( 2 , 4 ) сторон здания

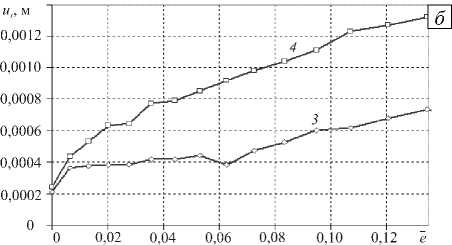
Рис. 5. Абсолютные вертикальные U z ( а ) и горизонтальные U x ( б ) смещения стенок здания в зависимости от безразмерного эксцентриситета e : смещения с левой (кривые 1 , 3 ) и правой ( 2 , 4 ) сторон здания

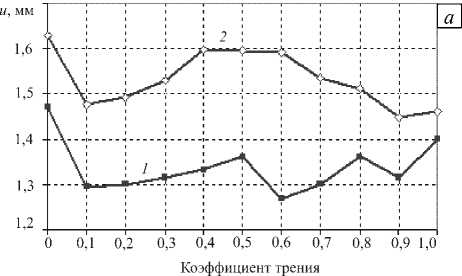
Рис. 6. Зависимость от коэффициента трения вертикальных U z (кривые 1 , 3 ) и горизонтальных U x ( 2 , 4 ) смещений сооружения, заглубленного на треть высоты ( а ) и полностью заглубленного ( б )

Коэффициент трения

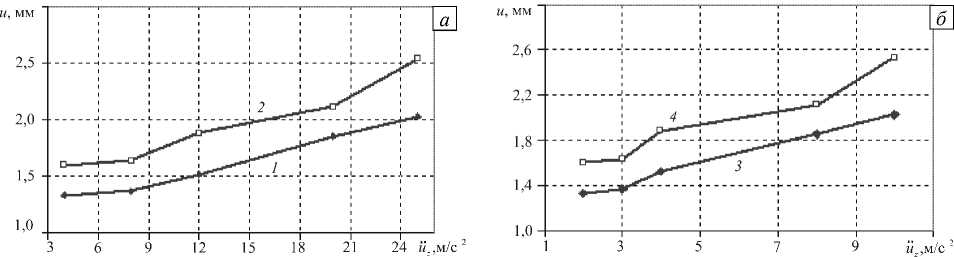
Рис. 7. Зависимость взаимных вертикальных uz (кривые 1, 3) и горизонтальных ux (2, 4) смещений сооружения и грунта от величины вертикальных (а) и горизонтальных (б) ускорений на поверхности грунта на вертикальные смещения для полностью заглубленных зданий. Зависимость взаимных смещений стенок сооружения и грунта от величины вертикальных и горизонтальных ускорений на поверхности грунта представлены на рисунке 7. Можно сделать вывод, что между ускорениями на поверхности грунта и взаимными смещениями грунта и здания имеется зависимость, близкая к линейной.

На основании серии численных экспериментов с многослойными грунтами установлено, что существенным для проведения расчетов на сейсмостойкость является геологическое строение среды на глубине до 8 величин заглубления сооружения в грунт. Численные исследования позволили оценить необходимую для геологических изысканий глубину разреза, в котором должны быть изучены механические характеристики слоев грунта.

Работа выполнена при финансовой поддержке Федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 2009-2013 годы, Совета по грантам Президента РФ для поддержки ведущих научных школ (грант НШ–4807.2010.8) и РФФИ (проект № 11-08-97023-р_Поволжье_а).