Численное моделирование аэродинамики стандартного коллектора тумана

Актуальность исследований новых альтернативных источников питьевой воды для обеспечения нужд живых организмов не вызывает сомнения. Так, более двух миллиардов человек в мире испытывают нехватку чистой воды [1]. Проблема усугубляется в регионах с малым количеством осадков и сухим климатом. В основном это территории африканских, азиатских и латиноамериканских стран. Альтернативные водные ресурсы именно здесь наиболее необходимы и экономически целесообразны [2].

Туман, один из широко используемых возобновляемых водных ресурсов, способен обеспечивать получение пресной и незагрязненной воды. Сбор воды из естественного [3–7] и промышленного тумана [8] коллекторами туманной воды (КТВ) — реальная и эффективная технология создания дополнительного водного ресурса.

Искусственные сооружения для сбора воды из тумана и росы и раньше строились во многих частях Земли. Руины таких сооружений располагались в пустынных регионах Средиземноморья и Южной Америки [9]. Например, в пустыне Атакама (Чили) замечены груды камней для сбора тумана. Тихоокеанское течение охлаждает нижние слои атмосферы, но с увеличением высоты вместо понижения

температура, наоборот, увеличивается. Этот природный феномен препятствует выпадению осадков, в результате образуются дымки, туманы. Ночью туман конденсируется на каменных структурах, а вода собирается в полости.

Подобные каменные артефакты обнаружены и на Крымском полуострове. Климатические условия на Крымском полуострове являются подходящими для внедрения технологии сбора тумана, который стабильно возникает в осенне-весенний период года. Выполненные в полевых условиях эксперименты [10] показывают перспективность способа получения воды из морского тумана вблизи Керченского пролива.

В последние годы изучению и совершенствованию технологии сбора тумана уделяется значительное внимание [11–16]. Исследователи ищут прототипы в природе и предлагают возможные решения, такие как конические поверхности [17], специальные арфы [18], сетки из полимерных волокон [19], колючие конусы и капиллярные симметричные каналы [20], морщинистые волокна [21]. Однако до сих пор открытые сетчатые ткани в обрамлении были единственными устройствами, которые широко применяются либо в полевых условиях [22–28], либо для сбора воды в тумане в исследовательских целях [5, 6].

Шеменауэр и Сереседа [22] предложили простой и недорогой туманоуловитель — стандартный крупномасштабный коллектор тумана (СКТ), который состоит из квадратной сетки площадью 1 м2. СКТ в основном находят приложения в коммерческих исследованиях для оценки количества водяного тумана, который может собираться в конкретном месте. В последующем были разработаны новые стратегии повышения эффективности сбора и созданы большие коллекторы тумана (БКТ). Комплектации СКТ и БКТ идентичны, но последний по горизонтали намного больше, чем по вертикали. В большинстве случаев сетка имеет высоту 4 м и длину 10 м. Наиболее часто в полевых условиях используется сетка Рашель (сетка с трапециевидной ячейкой), ориентированная вертикально между двумя держателями [29–31].

Общая эффективность сбора n coll определяется как произведение аэродинамической эффективности П ACE , эффективности осаждения n cap и эффективности дренажа n dr :

n coll = n ACE n cap n dr • ⁽¹⁾

Эффективность аэродинамического сбора n _ACE — это доля невозмущенного потока туманного воздуха, который потенциально может достичь волокон сетки [23]. Обычный коллектор тумана с сетчатым экраном создает боковое и верхнее отклонение течения, при этом более 60% капель туманной воды не попадают в сетку [26]. Этот эффект обусловлен сопротивлением, которое зависит от соотношения сторон сетки, аэродинамической характеристики волокон и узора плетения ячеек. Обход коллектора частью потока туманного воздуха является основным фактором, снижающим объем получаемой воды [24, 29, 32].

Эффективность осаждения n _cap — это доля капель тумана, которые фактически оседают на сетке. Твердые структуры, захваченные вместе с туманом, отклоняют поток, но капли тумана, вследствие их более высокой инерции, имеют способность мигрировать в потоке и взаимодействовать с волокнами. Эффективность осаждения возрастает с уменьшением диаметра волокна и увеличением скорости набегающего потока. Следует заметить, что n _cap может определяться также в виде отношения массы капель тумана, фактически собранных в коллекторе, к массе дрейфующих капель в невозмущенном входящем потоке тумана.

Эффективность дренажа n dr — доля объема воды, которая в конечном итоге достигает собирающего желоба. Капли тумана, достигшие сетки, могут повторно уноситься потоком. Поэтому существует утечка, которая приводит к разному количеству захваченных и собранных капель воды. На эффективность дренажа комплексно влияют смачиваемость сетчатого материала, диаметр капель и скорость набегающего потока.

Увеличение количества сеточных экранов — N , улучшает эффективность сбора вплоть до оптимального значения N = 3 + 5 [26]; при N >  5 туманоуловитель становится для потока туманного воздуха непроницаемым, вследствие этого его эффективность снижается. Азим и соавторы [33] выяснили, что максимальная аэродинамическая эффективность сбора достигается при использовании многослойных коллекторов (с 4-мя или 5-ю слоями).

Прямые экспериментальные измерения аэродинамической эффективности затруднительны: чтобы установить параметр, необходима информация о поле скорости вокруг коллектора и аэродинамических характеристиках коллекторной сетки. В этом случае инструментом может служить численное моделирование. Современные программные пакеты широко практикуются в инженерном проектировании и способны значительно ускорить процесс определения оптимальных параметров [34–37]. В работе [38] рассмотрена трехмерная вычислительная модель гидродинамики, в которой двухмерная двухслойная сетка коллектора представляется как пористая среда. Созданная в [39] система численного моделирования электростатически усиленного коллектора тумана используется для оценки его потенциала.

Основные трудности численного моделирования турбулентного потока воздушно-капельной смеси вокруг коллектора тумана заключаются в том, что приходится сочетать размеры волокна сетки и расчетной области, которые отличаются на несколько порядков. При этом вычислительные процессы требуют больших затрат времени и ресурсов, особенно при изучении двухфазного потока жидкость–газ.

Данная работа направлена на моделирование доминирующих во время сбора тумана физических процессов, а полученные результаты могут быть полезными при планировании как натурных, так и компьютерных экспериментов. Цель исследований заключается в следующем:

– выявить аэродинамическое поведение сетки, чтобы улучшить конструкцию коллектора для практического применения (в частности, оценить аэродинамическую эффективность сбора коллектора тумана и проанализировать распределение скорости и полного давления набегающего потока);

– смоделировать каждое волокно сетки с точностью до 10–4 м в пространстве, имеющем длину и ширину несколько метров, при этом для реализации вычислений вертикальный размер расчетной области берется минимально возможный, следовательно, постановку задачи можно считать двухмерной;

– выявить, как отражаются на коэффициенте аэродинамической эффективности сбора различные способы определения скорости потока (при моделировании решаются осредненные по Рейнольдсу уравнения Навье–Стокса с SST-моделью турбулентности).

Приведены результаты моделирования коллектора тумана с учетом геометрии волокна и размеров ячейки расчетной сетки, с помощью которой он аппроксимируется. Изучена зависимость аэродинамической эффективности от скорости потока, коэффициента затенения, числа слоев сетки коллектора и расстояния между ними.

• 2.    Методика проведения работы

  • 2.1.    Модель аэродинамической эффективности сбора

В реальном коллекторе часть потока проходит через сетку, а остальная часть отклоняется, обходит вокруг нее (Рис. 1 а ). В работе [23] предложена модель аэродинамической эффективности сбора, которую успешно применяли и другие авторы [15, 29]. Согласно модели, поток представляется как суперпозиция потока, который вынужден проходить только через сетку (Рис. 1 б ), и потока, который при движении огибает сплошной экран (Рис. 1 в ). Согласно правилу суперпозиции, скорость невозмущенного набегающего потока u ₀ равна сумме скорости потока, вынужденного проходить через сетку u ₁ , и скорости u ₂ при непроницаемом экране:

u 0 = u 1 + u 2 . (2)

При этом площади сетки и экрана одинаковы и равны A ₁ . На рисунке 1 а показано расположение волокон в поперечном сечении расчетной ячейки: волокно прямоугольной формы (в один или два ряда, вставка 1 ) или круглой (в один ряд, вставка 2 ). Предположение о суперпозиции потоков не является строго выполняемым. Как видно на рисунке, линии тока не параллельны, особенно в области перед непроницаемым экраном (Рис. 1 в ). Кроме того, не совсем понятна формулировка и способ измерения скорости потока u ₁ , проходящего только через сетку. Чтобы уменьшить присущую модели из [23] погрешность и не выполнять расчет для непроницаемого экрана, в данной работе предлагается скорость невозмущенного набегающего потока u 0 представить как сумму: и 0 = u 1 + и 2 , где и 1 и u 2 — скорости частей потока, соответственно, пересекающей сетку и отклоняющейся от нее (Рис. 1 а ) [15].

Вход Mi

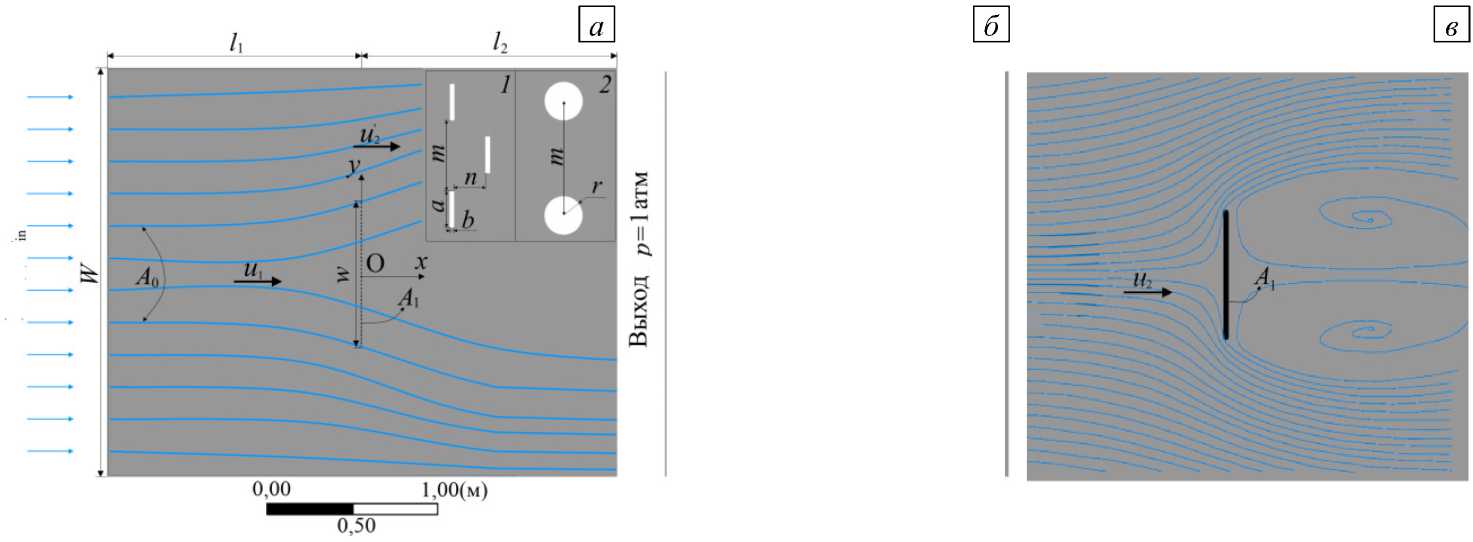
Рис. 1. Геометрия и размеры области моделирования в реальном случае (на вставке в увеличенном масштабе показаны поперечные сечения волокна сетки: 1 – прямоугольное, 2 – круглое (а); вид потока, который вынужден проходить только через сетку (б); вид потока при наличии на его пути непроницаемого экрана (в)

Далее в модифицированной модели аэродинамической эффективности сбора рассмотрим поток (Рис. 1 а ) в предположении постоянства его плотности р и выполнения условия:

и 0 A o = U 1 A 1 ,                                                    (3)

где A ₀ — площадь невозмущенной области потока, которая подходит к сетке, а A ₁ — площадь сетки (Рис. 1 а ). Условие (3), являющееся уравнением непрерывности, справедливо приближенно, так как не учитывает внешние потоки.

Согласно модели [23], эффективность аэродинамического сбора n ACE определяется как

П ACE = sA /A1, где s = 1 - f — коэффициент затенения, при этом f = Aop[ A — отношение площади свободного потока Aop , равной площади отверстий сетки, к общей площади сетки A1 . C учетом (3) получим:

ПACE = su1 lu0 .

Для того чтобы перейти к зависимости n _ACE только от геометрических размеров, найдем разность давления P между наветренной и подветренной сторонами СКТ, которая для сетки равняется

AP = Cop и2/2,(6)

где C ₀ — коэффициент потери давления на сетке, а для сплошного экрана составляет:

AP = Cd р u2/2,(7)

при этом C_d — коэффициент лобового сопротивления сплошного экрана.

Предположим, что разность давлений в уравнениях (6) и (7) одинакова:

C0 и2 = Cdu2.(8)

Подставляя u ₂ из уравнения (2) в (8) и решая это квадратичное уравнение, получим:

и0 /и = 1 ± VC0/Cd .(9)

Далее (9) рассматривается только с положительным знаком, так как поток перед сеткой испытывает сопротивление и тормозится, поэтому и ₀ >  и 1 . С учетом этого условия из формулы (5) будем иметь:

nACE = sl(1 + С <) .(10)

Коэффициенты лобового сопротивления C_d двух- и трехмерных объектов тщательно изучены и представлены в большинстве справочников по механике жидкости и газа. На величину C_d прямоугольных пластин влияет только соотношение сторон. Труднее определить коэффициент падения давления C ₀ , поскольку он зависит от параметров сетки: отношения площадей f , характеристик волокон и их переплетения. Для типичной полиэтиленовой сетки Рашель [23]:

С 0 = 1,62 ( 1,3 ( 1 - f ) + ( ( V f ) - 1 ) ² ) = 1,62 ( 1,3 s + ( s / ( 1 - s ) ) ² ) .                       (11)

В разных странах в основном используется полипропиленовая или полиэтиленовая сетка с коэффициентом затенения 35%. С одной стороны, большое значение коэффициента затенения s подразумевает больший физический перехват встречного потока волокнами, и, таким образом, значительная часть встречного тумана оседает на сеточных волокнах, что способствует лучшему сбору воды. С другой стороны, увеличение s приводит к росту оказываемого сеткой сопротивления, и, как следствие, к отклонению потока за пределы туманоуловителя и снижению его производительности. Оптимальное значение коэффициента затенения зависит от материала сетки (проволочная или нитяная), переплетения (ячейка треугольной или прямоугольной формы), а также от геометрии и ориентации коллектора тумана.

• 2.2.    Основные уравнения

Итак, требуется определить скорость и полное давление набегающего на коллектор потока тумана. Для решения используется одна из моделей вычислительной гидродинамики — модель RANS, включенная в программный пакет ANSYS CFX, которая основывается на нестационарных уравнениях Навье–Стокса, усредненных по Рейнольдсу. Эти уравнения применяются для моделирования турбулентных воздушных потоков и в других открытых вычислительных комплексах [40].

Согласно модели RANS скорость турбулентного течения U разделяется на среднюю по времени или пространству составляющую — U , и пульсационную — u :

U = U + u .

Средняя составляющая по времени задается формулой:

1 t + Д t

U = — f Udt, Δt t где Δt — масштаб времени t , который велик по отношению к турбулентным флуктуациям, но мал по сравнению со временем, в течение которого решается задача.

Для отыскания поля средней скорости в зависимости от координат запишем: – уравнение неразрывности

^- ( p U ) = 0,                                (12)

d t где V — оператор Гамильтона;

– уравнение количества движения

^^ + V-(pUU) = -VP + V-(t-puu) + SM ,                      (13)

где t = p ( v U + ( V U ) ^t - ( 2/3 ) 5V U ) — тензор вязких напряжений (при этом ц = 1,831 - 10 5 Па^с — коэффициент динамической вязкости, 5 — символ Кронекера, буква T — знак транспонирования), S М — источник импульса (реализуется в ANSYS CFX как дополнительная сила, действующая на единицу объема); – уравнение энергии

М|У-|Р ₊ V- ( p U h_tot ) = V- ( XV t ) + v ( U ( T -p UU ) ) + S E ,                  (14)

где h _ol и h stat — полная и статическая энтальпии, Х = 0,0261Вт/(м^К) — коэффициент теплопроводности, S _E — внешние источники энергии (в настоящей работе во внимание не принимаются). Полная и статическая энтальпии связаны соотношением: h_tot = h_stat + U ²/2 + k , при этом k = u ²/2 , h_s iai = c P T = 1004,4 - 298 = 299,3 кДж/кг, c P — удельная теплоемкость при постоянном давлении, T — температура.

Для изотермических условий моделирования (при T = 298 К) уравнение состояния р = р(T,P) имеет вид: р = ( PM)/(RT), где M = 28,96 кг/кмоль — молярная масса воздуха, R = 8,31 Дж/(молыК) — универсальная газовая постоянная.

Для решения задачи используется численный метод, основанный на дискретной аппроксимации уравнений. Согласно методу, на каждой итерации целевая функция и параметры состояния представляются в виде квадратичных функций. На каждой последующей итерации начальной информацией о целевой функции и переменных состояния служит установленная на предыдущей итерации. Расчетная сетка имеет элемент со стороной 5,5 мм. Для времени берется физическая шкала с шагом 0,1 с.

• 2.3.    Физические условия

В работе рассмотрен СКТ (далее просто коллектор). Вводилась декартова система координат Oxyz , где ось Ox совпадала по направлению с начальным невозмущенным потоком туманного воздуха, Oy ориентировалась поперек его, а Oz — по нормали к плоскости сетки. Начало координат находилось в центре сетки, которая располагалась на расстоянии 11 = 1,5 м от входа потока туманного воздуха и 12 = 1,5 м от его выхода (Рис. 1 а). В поперечном потоку направлении ширина сетки коллектора составляла w = 1м, а ширина расчетной области равнялась W = 2,4 м. Продольный размер зависел от формы волокон. Волокна в сечении представляли или прямоугольники размерами a = 1 мм и b = 0,1 мм, или круги радиуса r = 1 мм (см. Рис. 1 а, вставка). Коэффициент затенения устанавливался путем изменения ширины отверстий сетки m = (0,25 ^ 4) мм. В зависимости от коэффициента затенения линейная плотность сетки составляла от 170 до 800 элементов на погонный метр. Плотность двухслойных сеток была вдвое больше.

Формирование задачи в препроцессоре пакета ANSYS CFX начинается с задания свойств исследуемой жидкости и абсолютного значения (опорного) давления, от которого ведется отсчет всех остальных значений давления в решателе программы. Моделирование выполнено для потока двухфазной однородной среды, компонентами которой являлись воздух и вода. Капли воды имели диаметр 20 мкм, плотность тумана равнялась 0,2 г/м3 (эти величины выбраны в соответствии с известными работами по моделированию аэродинамики коллекторной сетки [33, 38], опорное давление — 1 атм, скорость потока на входе 3÷7 м/с (в соответствии с экспериментом), статическое давление на выходе — 1 атм (нормальное атмосферное давление). Турбулентное поведение потока описывалось моделью Shear Stress Transport (SST), которая хорошо зарекомендовала себя при расчете течения как вблизи стенок, так и в потоке в целом. Она устойчива и не требует больших вычислительных ресурсов.

Заявленная в данной работе расчетная модель сочетает в себе масштабы, отличающиеся на четыре порядка: от величины элементов сетки коллектора (0,1 мм) до размеров области аэродинамического моделирования (1÷3 м). При осуществлении решения поставленной задачи выбрано оптимальное соотношение физических параметров и вычислительных мощностей, доступных авторам. Размеры коллектора задавались так, чтобы исключить их влияние на искомые поля скорости.

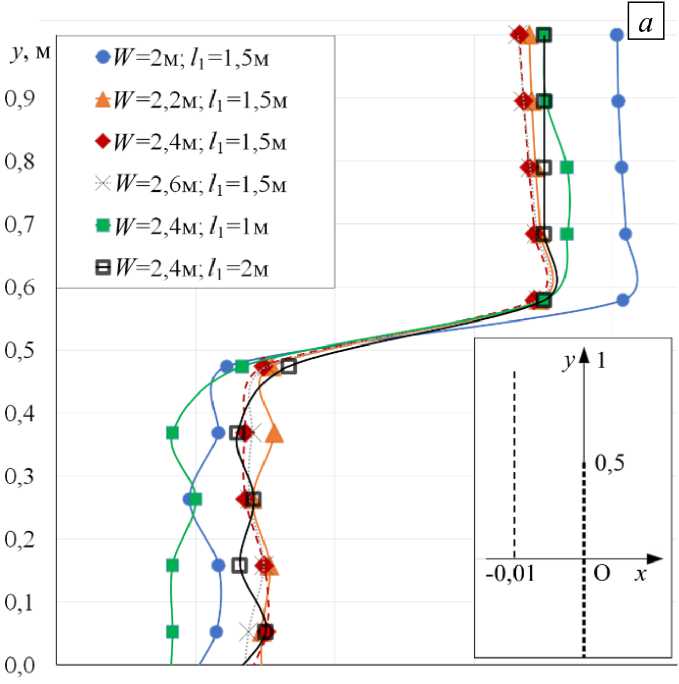
На рисунке 2 а приведен график зависимости u — средней скорости, нормированной на скорость невозмущенного потока u ₀ , от координаты y для четырех значений ширины W и трех местоположений l ₁

сетки коллектора. Расстояние от сетки до выхода оставалось постоянным: 12 = 1,5 м. Результаты получены для un = и0 = 3 м/с в точках с координатой x = 0,01м, через которые перед сеткой проведена штриховая линия (см. Рис. 2а, вставка). При изменении ширины и длины области моделирования сравнивались только распределения скорости при у = 1м от центра сетки, то есть координате у = 0 ^ 0,5 м соответствует скорость потока у сетки коллектора, а у = 0,5 ^ 1м — сбоку от нее (Рис. 2а). Аналогично подбирались 11 и 12. Дальнейшее увеличение этих размеров не вносило изменений в распределение скорости около коллектора.

Для проверки зависимости результатов от размеров ячеек расчетной сетки тестировались сетки с различной плотностью узлов и фиксировалось распределение скорости течения. В среднем расчетная сетка состояла из 0,4 млн элементов и 0,2 млн узлов (Рис. 2 б ). Уменьшение размеров элементов в 2 раза приводило к изменению скорости не более чем на 4%. Таким образом, при малых коэффициентах затенения s , то есть при больших интервалах между волокнами сетки m и n (Рис. 1 а , вставка), использовалась более грубая сетка. При измельчении сетки (увеличении коэффициента затенения s ) применялась расчетная сетка 0,8 млн элементов и 0,4 млн узлов, при этом ее ячейки были меньше m и n — характерных расстояний сетки коллектора.

0,95         0,97         0,99         1,01 и!и_й

Рис. 2. Зависимость нормированной скорости потока воздуха

б

0,25        0,75

u от координаты y ( а ) (на вставке показана схема

расположения сетки в коллекторе и место точек (штриховая линия), в которых вычислялась u ); расчетная сетка для работы в пакете ANSYS CFX при разной форме сеточного волокна ( б )

• 3.    Результаты и обсуждение

  • 3.1.    Скорость потока

Распределение скорости потока в расчетной области показано на рисунке 3. В соответствии с ним далее выбирались значения скорости для расчета ц _АСЕ . Следует отметить, что принцип суперпозиции скоростей, который положен в основу модели из [23], не выполняется. Так, согласно (1), для нахождения эффективности аэродинамического сбора рассматривается двумерный поток в области коллектора, установленного очень высоко над землей. При этом на входе скорость невозмущенного набегающего потока есть и 0 , а в обсуждаемом случае скорость на входе и in , составлять сумму двух скоростей: u 1 и и 2 .

Однако спад скорости с приближением к сетке не столь стремителен, чтобы выполнилось равенство (2),

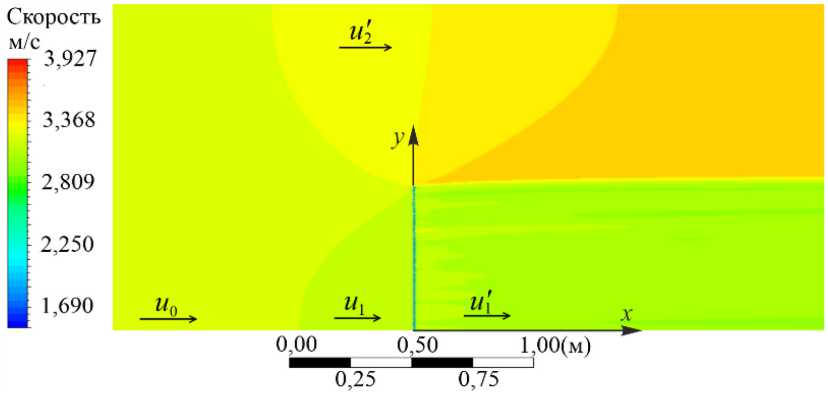
Рис. 3.

Контурная диаграмма распределения скорости в модели коллекторной сетки (в силу симметрии задачи показана только ее половина)

особенно при малых коэффициентах затенения (до s = 0,5 ) . Поэтому, если к скорости u ₁ добавить u ₂ — скорость возле непроницаемого экрана, получится значительно большая, чем u ₀ , величина. Для проверки этого утверждения выполнен расчет течения только при наличии непроницаемого экрана (Рис. 1 в ). В осуществленных вычислительных экспериментах и2 — скорость по краям, всегда больше скорости невозмущенного потока u ₀ , а сумма и 1 и и 2 тем более.

Принцип суперпозиции выполняется, если в расчете используется средняя скорость потока после сетки коллектора. На рисунке 3 эта скорость обозначена как и ’ . Были проанализированы два подхода к определению ц _ACE . В первом случае в расчет принимались значения скорости на бесконечности ( и 0 ) и средней скорости потока перед сеткой коллектора ( и 1 ) . Во втором подходе и 1 заменялась и ’ . Тогда для вычисления ц _ACE достаточно только уравнения (5). Скорости и 0 , и 1 и и ’ находились при разных значениях коэффициента затенения и двух конфигурациях волокон: лентообразной и цилиндрической.

На рисунке 4 представлены зависимости ц _ACE от коэффициента затенения s . График соответствует однослойной сетке с лентообразными волокнами шириной a = 1мм и толщиной b = 0,1мм (Рис. 1 а , вставка, форма 1 ). Расстояние m между лентами коллектора менялось в пределах 4 до 0,25 мм, что приводило к увеличению s . Скорость на входе равнялась и 0 = 3 м/с. Зависимость ц _ACE = f ( s ) , рассчитанная по формуле (5) при использовании u ₁ (Рис. 4 а ), при некотором значении s имеет максимум. Для нахождения числового значения коэффициента затенения s _max , на который приходится максимум аэродинамической эффективности n max , кривая f ( s ) аппроксимировалась полиномом вида:

n _ACE = - 0,354 s ³ - 0,620 s ² + 1,137 s + 0,012.

Определялась производная f '( s ) и приравнивалась нулю:

- 1,062 s ² - 1,240 s + 1,13 7 = 0.                                     (16)

Положительный корень уравнения (16) и являлся максимальным значением коэффициента затенения: s max = 0,593. После его подстановки в (15), получилось: n max = 0,370 . Расчеты выполнены еще для двух скоростей и 0 . Количественно это выражается так: скоростям и 0 = 3 ^ 7 м/с соответствуют s max = 0,593 ^ 0,599 и n max = 0,370 ^ 0,372. (Рис. 4 а ). Как видно, разница в значениях коэффициента затенения, на который приходится максимум n _ACE , составляет тысячные доли. Таким образом, использование средней скорости в области перед сеткой u ₁ (Рис. 3) в соотношении (5) показывает, что n _ACE слабо зависит от и 0 .

Для сравнения выполнен расчет n _ACE = f ( s ) по средней скорости потока после сетки коллектора тумана — и ’ (Рис. 4 б ). При таком способе определения ц _АСЕ и скорости невозмущенного потока и. = 3 ^ 7 м/с максимальные значения параметров составили: s_m„„ = 0,524 ^ 0,483 и и _v = 0,296 ^ 0,306. 0                                                                                        max                              max

Видно, что с увеличением скорости и 0 для достижения максимальной n _АСЕ нужна меньшая величина коэффициента затенения, при этом наибольшей эффективности отвечает значение n max меньшее, чем при ее расчете по и 1 (Рис. 4 а ). Средняя скорость перед сеткой ( и 1 ) всегда больше скорости после нее ( и ’ ) для любых значений коэффициента затенения. Таким образом, результаты n max ближе к экспериментальным данным. Кроме того, более явной становится зависимость как s max , так и n max от скорости u ₀ , что также соответствует практическим исследованиям.

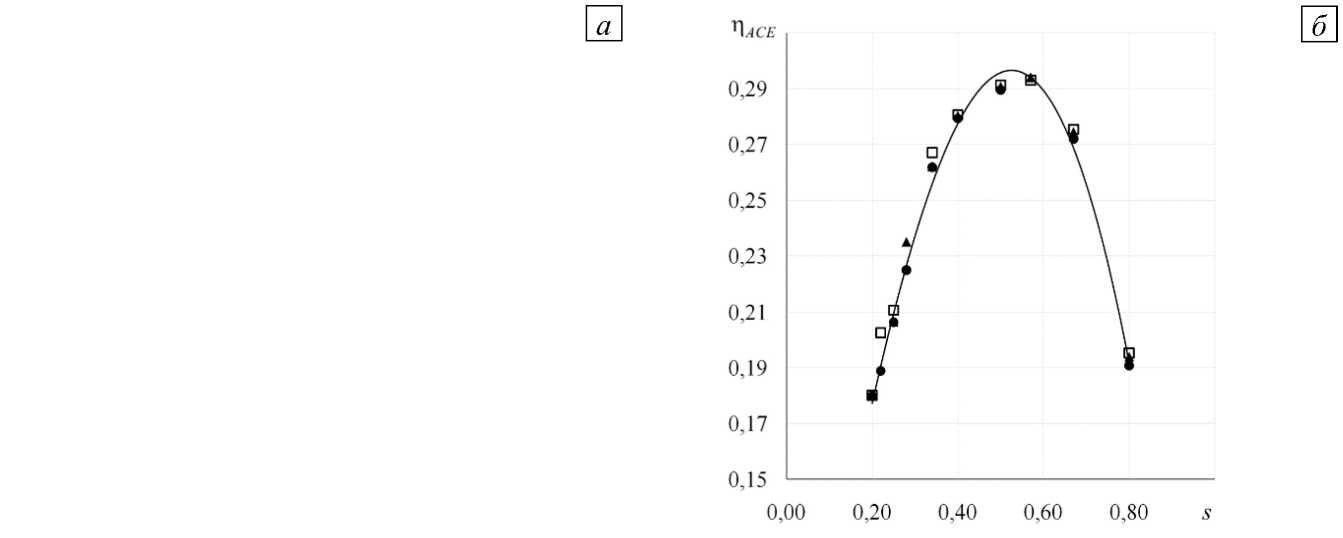
Рис. 4. Аэродинамическая эффективность сбора как функция коэффициента затенения, рассчитанная согласно уравнению (5) по средней скорости перед сеткой и 1 ( а ) и после сетки и ’ ( б ) и разных значениях и ₀, м/с: 3 (маркер • ), 5 ( ▲ ), 7 (□)

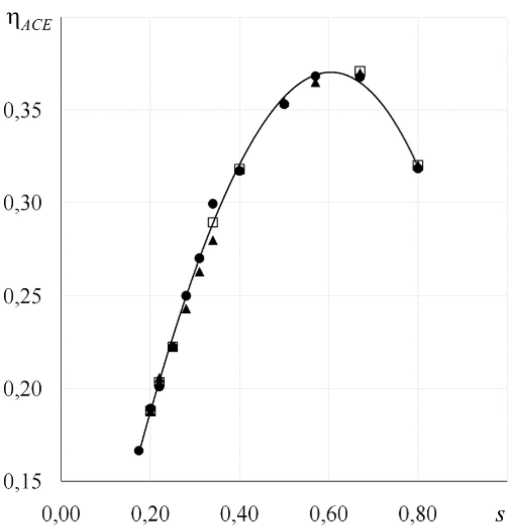
Подобные расчеты, но только для коллектора с волокнами цилиндрической формы (Рис. 1 а , вставка 2 ) при r = 0,5 мм и этом же интервале скоростей показали результаты: s max = 0,586 ^ 0,590 и n max = 0,373 ^ 0,377 . Переход от сетки с лентообразными волокнами к сетке с волокнами цилиндрической формы существенно влияет на поток между волокнами сетки. Однако на расстоянии от коллектора усредненные значения скорости в большей степени зависят от размеров, а не от формы элементов сетки.

Полученный результат n max и соответствующее значение коэффициента затенения хорошо согласуются с данными, в основу которых положен численный расчет в пакете ANSYS CFX. Максимальная эффективность аэродинамического сбора n _ACE отвечает s , равному 0,570 и 0,540, соответственно, для вогнутого и плоского коллекторов [23]. Путем компьютерного моделирования установлено, что самую высокую эффективность ( n _ACE = 0,38) имеет сетка с s = 0,6 и цилиндрическими волокнами диаметром 1 мм [23]. Экспериментальные данные свидетельствую о том, что n _ACE может быть легко улучшена до максимального значения 0,245^0,280, если s = 0,55 [25]. Результаты измерений в процессе полевых экспериментов по сбору тумана существенно ниже получаемых численно. Если оптимальная величина коэффициента затенения отличается на 6^7%, то экспериментальное значение максимальной n _ACE ниже на 28÷35% значений, которые дает численная модель пакета ANSYS CFX. Расхождение результатов можно объяснить особенностями модели коллектора: в численных экспериментах рассматривается двухмерная сетка, потоки сверху и снизу коллектора отсутствуют, что приводит к увеличению n _ACE • Кроме того, в большинстве исследований во всем мире за основу берется сетка Рашель, переплетение которой представляет вытянутые по вертикали треугольники, что также не учитывается в двухмерной модели.

• 3.2.    Двухслойный коллектор тумана

Два последних десятилетия в коллекторах тумана применяется двухслойная сетка, поскольку она обеспечивает более высокий выход воды. Чтобы прийти к формуле для определения n _ACE , используются три предположения [33]. Во-первых, входящий поток как в дальнем поле, так и непосредственно перед коллектором ортогонален его поверхности. Во-вторых, подразумевается, что сетку коллектора образуют однонаправленные волокна, то есть сетка подобна арфе. В-третьих, в многослойной сетке расстояние между слоями достаточно велико, поток тумана не успевает восстановить однородность перед достижением следующего слоя. В таком случае n _ACE предлагается рассчитывать по формуле [33]:

n ACE = ( uu 0 ) ( 1 - ( 1 - s ) N ) ,

где N — число слоев сетки.

0          2           4 п/Ь

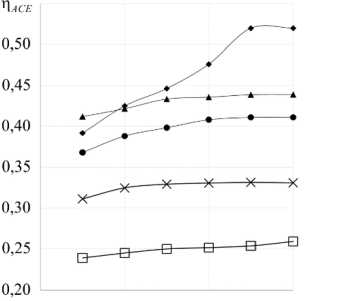
Рис. 5.            Аэродинамическая эффективность сбора nace, рассчитанная по уравнению (17) при разных значениях коэффициента затенения s : 0,33 (•), 0,4 (♦), 0,5 (▲), 0,67 (х), 0,8 (□)

соответствует изменению характера

Рассмотрена двухслойная сетка, показанная на рисунке 1а (см. вставку 1). Полосы второго ряда располагались напротив промежутков между полосами первого слоя сетки. Расстояние n между слоями варьировалось при постоянных s и u0 . На рисунке 5 приведены кривые nACE, построенные по данным расчета согласно (17) для пяти коэффициентов затенения. Увеличение расстояния n между слоями в пределах 1–4 мм приводит к росту nACE. Как показано в [33], оптимальное расстояние между слоями составляет от 6 до 9 мм, что, как минимум, в 40 раз превышает характерную толщину слоев стандартного коллектора. Авторами данной работы получено, что по абсолютной величине зазора n > 5 мм эффективность ПACE ~ const. В относительных величинах стабильность nACE достигается при n/b > 50. Наиболее стремительный рост и максимальная величина nACE соотносятся с s = 0,4. При этом nmax = 0,520, что почти в 2 раза больше, чем при однослойной сетке. Отличная от других кривизна графика при s = 0,4 обусловлена тем, что данный коэффициент затенения кривой: дальнейшее увеличение приводит к снижению результирующего nACE .

В работе сделана оценка выполнения предположений, сформулированных выше при выводе соотношения (17). Для анализа величины и направления скорости тумана перед коллектором и между слоями его сетки на плоскости коллектора выбирались характеристические точки числом 109 и в каждой определялись значения искомых параметров.

Рисунок 6 содержит информацию о направлении векторов скорости потока при и ₀ = 3 м/с. Векторное поле скорости, полученное при моделировании в ANSYS CFX, показывает, что ортогональность потока соблюдается только в центре коллектора (Рис. 6 a ). Чем ближе к краю его сетки, тем больше касательная составляющая скорости (Рис. 6 б ). При n/b >  50 величина эффективности n _ACE остается постоянной, и восстанавливается направление векторов скорости между слоями сетки. При этом в центре поток перпендикулярен второму слою сетки, а ближе к краю коллектора сохраняет угол падения на первый слой.

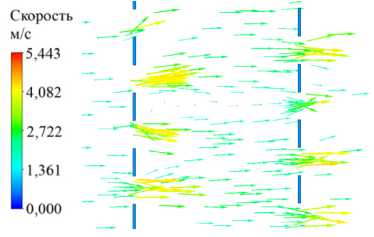
относительное расстояние между слоями n/b = 50

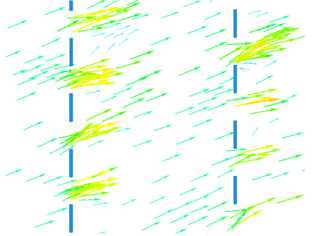
Рис. 6. Векторное поле скорости в центре ( а ) и на краю ( б ) двухслойной сетки коллектора; скорость на входе и ₀ = 3 м/с,

Изменение угла с приближением к краю коллектора приводит к снижению n _ACE . Тогда равенство (3) будет иметь вид: и ₀ A ₀ = u 1 A 1 sin а [8]. Угол а откладывается от поверхности коллектора. С учетом этого выражения n _ACE в центре и на краю могут отличаться в 7 раз для s = 0,8 и в 1,1 раза для s = 0,2 . Поэтому целесообразнее делать коллектор тумана вогнутым: он имеет большую эффективность аэродинамического сбора за счет уменьшения угла вектора скорости относительно нормали к поверхности на его краях.

• 3.3.    Перепад давления

Чтобы выполнить анализ влияния геометрии и размеров ячеек сетки коллектора на эффективность аэродинамического сбора, необходимо знать давление, оказываемое набегающим потоком на сетку. Перепад давления AP между передней и задней поверхностями сетки — еще одна важная характеристика аэродинамики потока. Следует отметить, что в основу вывода формулы (10) для вычисления nACE положено равенство AP, рассчитываемых по (6) и (7). Однако, согласно авторским данным, перепад давления на сплошном экране (Рис. 1в) больше, чем на сетке таких же размеров (Рис. 1а). Путем численных экспериментов получены контуры полного давления Ptot в области коллектора. Полное давление отсчитывалось от опорного давления 1 атм, как и в эксперименте. Распределение Ptot , нормированного на динамическое давление невозмущенного потока ри2 /2 , при и0 = 5 м/с и s = 0,67 приведено на рисунке 7а (далее для нормированного давления оставлено то же самое обозначение). Качественно вид поля полного давления при всех коэффициентах затенения s и скоростях u0 , используемых в работе, отличается слабо. Во всех случаях можно выделить три области, в которых полное нормированное давление Ptot = const. Стабильность Ptot в области до и после коллектора при изменении других параметров можно видеть на рисунке 7б. Графики Ptot в зависимости от координаты x для разных значений коэффициента затенения позволяют точно определить перепад давления ^Р.

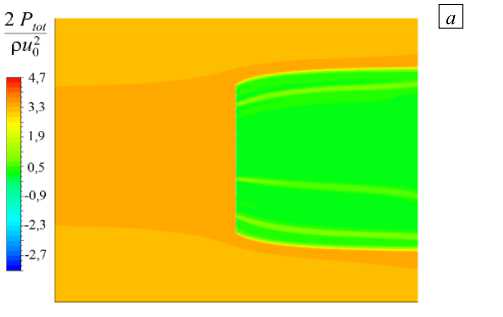
Рис. 7. Контурная диаграмма распределения нормированного полного давления ( а ); график P_tot в центре модели ( б )

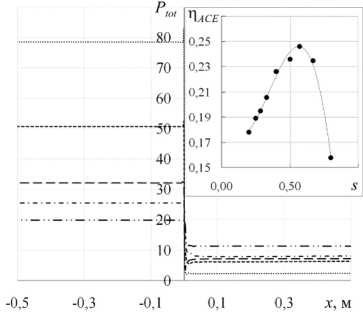
б

(расчет при у = 0 , и0 = 5 м/с и разных значениях s : 0,8 (•••), 0,67 (---), 0,5 (--), 0,4 (-•-), 0,25 (-••-)); на вставке зависимость nACE = f (s) согласно уравнению (14)

Теоретическая модель аэродинамики сбора тумана предложена Риверой [23] для прогнозирования эффективности сеток, ориентированных перпендикулярно потоку. В такой конфигурации аэродинамическая эффективность сетки коллектора определяется по уравнению (10) и зависит от коэффициентов лобового сопротивления ( C_d ) и потери давления ( C ₀ ) . Если C_d при заданных размерах сплошного экрана — величина известная, то C ₀ требуется определять для каждой конкретной сетки, то есть по отличающимся формулам, вывод которых носит эмпирический характер (как, например, формулы (11) для сетки Рашель). При этом погрешность расчета коэффициента потери давления оказывается существенной.

В данной работе в расчетах не использовались коэффициенты потери давления на сетке C0 и сопротивления сплошной пластины Cd, поэтому nACE выражалось через полное давление. Из уравнения (6) следует, что Ptot ~u2 , тогда n ACE = s 4 Ptot ,1 IP ,0 . (18)

Результаты расчета n _ACE показаны на вставке рисунке 7 б . Для функции (18) осуществлены исследования по аналогии с выполненными для уравнений (15) и (16): при и ₀ = 3 ^ 7 м/с найдены диапазоны значений s max = 0,85 ^ 0,554 и n max = 0,246 ^ 0,268.

Применение полного давления, а не скорости потока для расчета n _ACE дает ее более сильную зависимость от величины коэффициента затенения, на которую приходится максимум n _ACE при разных значениях и ₀. Однако n _max ниже, чем в численных экспериментах (см. Рис. 4). На контурной диаграмме (Рис. 7 а ) четко видны три области, где P_tot остается постоянным, в отличие от шести контуров распределения скорости (см. Рис. 3). Величина P_tot не изменяется перед сеткой коллектора, за ним и в области вдали от него. Были построены графики, подобные изображенным на рисунке 7 б , для всех рассмотренных в работе геометрических и физических параметров, которые позволили сделать вывод: полное давление вдоль поверхности коллектора меняется не более, чем на 0,3%. Поэтому из-за меньшего разброса данных для вычисления n _ACE целесообразнее использовать полное давление.

Для двухслойной сетки эффективность рассчитывалась как n ACE = V Pot ,11 Pot ,0 (1 -(1 — » ) N ) .                                          (19)

Относительное расстояние составляло n/b = 50, то есть поток после прохождения первого слоя сетки коллектора успевал восстановится до состояния перед сеткой, и n _ACE не зависело от n . Результаты представлены в таблице. Как и ожидалось, при одинаковом значении коэффициента затенения n _ACE двухслойной сетки выше, чем однослойной. В целом же каждое конкретное значение будет зависеть от множества факторов: смещения одного слоя относительно другого, угла падения потока, толщины волокон сетки и их деформации. Эти факторы будут вносить определенный разброс в данные вычислений.

Таблица. Коэффициент аэродинамической эффективности двухслойного коллектора, рассчитанный по формуле (19)

s	0,25	0,4	0,5	0,67	0,8
Л ACE	0,35	0,39	0,41	0,42	0,34

Тем не менее, в практических испытаниях рекомендуется определять n _ACE из уравнений (5) или (18) по измеренным скорости или полному давлению невозмущенного потока туманного воздуха и после сетки коллектора. В настоящее время существуют приборы, способные с достаточной точностью измерять необходимые для расчета величины. Выполненные авторами первые эксперименты по сбору тумана в полевых условиях Керченского полуострова [10] показали, что за 30 дней наблюдений n _ACE для коллектора с 5 = 0,2 [15] изменялась в интервале 0,179-0,184, и с этим согласуются результаты моделирования, полученные в данной работе (Рис. 4 б ). Скорость потока вдали от коллектора за время опытов варьировалась в пределах: и ₀ = 1 + 7 м/с. Общая эффективность сбора (1) с учетом осаждения и дренажа в коллекторе) составила n _coll = 0,045. В работе [15] сообщается, что в лабораторных экспериментах улавливания тумана коммерчески доступными сетками типа Рашель с 5 = 0,3 ^ 0,4 достигнута максимальная величина n _ACE = 0,28, общая эффективность сбора не превышает n _coll = 0,2. Однако в этих исследованиях эффективность дренажа n dr принимается равной 1, что не соответствует реальным условиям сбора тумана.

4.    Заключение

Методом численного моделирования выявлены основные закономерности аэродинамики потока туманного воздуха в области стандартного коллектора тумана. Решена проблема объединения масштабов параметров, различающихся на четыре порядка, что позволило уйти от моделирования коллектора тумана как пористой среды и точно задавать коэффициент затенения. Полученные зависимости n _ACE = f ( 5 ) позволили сделать следующие выводы:

• 1.    Подход к определению скорости потока, вынужденного проходить через сетку, может привести к разбросу данных при вычислении n _ACE ■ Выявлено, что использование в расчете n _ACE среднего значения скорости потока в области после коллектора приводит результаты вычислений в соответствие с экспериментальными.

• 2.    Рассчитанное векторное поле скорости показывает, что ортогональность потока соблюдается только в центре коллектора. С приближением к краю сетки поток отклоняется от нормального направления, что приводит к снижению n _ACE ■ Угол падения туманного воздуха сохраняется между слоями двухслойных сеток, если относительное расстояние nb превышает 50.

• 3.    Величина полного давления P_tot не изменяется перед коллектором, за ним и в области вдали от него. Контуры областей равных давлений имеют точные границы, и значение P_tot не зависит от места измерения около коллектора.

Полученные результаты численного моделирования будут полезными при анализе различных видов аппроксимирующих сеток, применяемых при исследовании коллекторов туманного воздуха. Используемый авторами подход позволяет усовершенствовать планирование реального эксперимента, так как при известном коэффициенте затенения коллекторной сетки достаточно выполнить измерения скорости потока вдали от коллектора и сразу за ним. Таким образом исключается одно неизвестное, необходимое при расчете общей эффективности сбора тумана (1), которая зависит также от эффективности осаждения и дренажа коллектора.

Работа выполнена при финансовой поддержке Керченского государственного морского технологического университета по контракту № 121032200168-6.