Численное моделирование деформирования и разрушения металлов в условиях плоского удара

В настоящее время основой большинства сооружений и изделий машиностроения являются металлы, поэтому исследование поведения в условиях ударного сжатия именно этих материалов чрезвычайно актуально. Достигнутые за последние годы успехи в понимании механизмов формирования ударных волн в сплошных средах способствовали развитию механики и физики твердого тела и практическому применению теории ударных волн в самых различных областях науки и техники, в частности военной. Здесь постоянно возникает необходимость изучения свойств металлов, используемых при изготовлении новых образцов вооружения, испытывающих в процессе эксплуатации ударные нагрузки. Результаты исследования материалов при динамических воздействиях открывают новые возможности для улучшения прочности средств бронезащиты.

Наблюдения за поведением материала при деформировании и разрушении в условиях ударного сжатия позволяют понять суть происходящих в материале процессов. Но, несмотря на то, что на сегодняшний день в этом направлении ведутся активные разработки, законченной теории разрушения при динамическом нагружении пока не существует. Можно выделить несколько направлений в моделировании процесса разрушения.

Одними из первых были разработаны критериальные модели [1], в основе которых лежит пороговый критерий, по достижении которого происходит разрушение. Но, при всей простоте и широкой применимости, у критериальных моделей есть существенный недостаток — они не способны учитывать эволюцию структуры материала. Дислокационные модели [2] лишены этого недостатка, поскольку в них полагается, что процесс пластического деформирования обусловлен движением мезоскопических дефектов (дислокаций). Следует отметить, однако, что реализация дислокационных моделей в массовых расчетах затруднена в связи с необходимостью определения многочисленных констант дислокационных соотношений.

В последние годы при моделировании деформирования и разрушения металлов наиболее популярным стал метод молекулярной динамики (МД) [3, 4]. Но при всех преимуществах МД-моделирования оно не является достаточным для исследования процесса в целом, так как применимо на сравнительно небольших пространственных масштабах, тогда как основные механизмы, влияющие на процесс деформирования, могут выходить за границы рассматриваемого масштаба.

Как известно, под воздействием нагрузки дефекты имеют способность зарождаться, расти и взаимодействовать, вследствие чего формируются дислокационные субструктуры различного типа, существующие в определенном диапазоне дислокационной плотности. Переходы от одного типа к другому приводят к резкому изменению механических свойств материалов. В связи с этим в лаборатории физических основ прочности ИМСС УрО РАН построена теория среды с дефектами и предложена математическая модель поведения материала при различных видах нагружения [5–11]. В модель введены два параметра порядка, которые описывают дефектную структуру материала. Первый — тензорный параметр, отвечает за плотность мезодефектов, а второй является структурным параметром, зависящим от отношения двух масштабов: размера скоплений дефектов и расстояния между скоплениями.

Данная работа не выходит за рамки предложенного подхода и ставит целью изучение поведения материалов при ударно-волновом нагружении с учетом особенностей изменения структуры. Моделирование этого процесса проводилось на основе уже существующей модели [7, 8]. Модификация заключалась в разделении полных напряжений на шаровую и девиаторную части, что позволило учесть влияние каждой из этих составляющих на деформирование материала в целом. Также в работе предлагается новый вид критерия откольного разрушения. Объектом моделирования являются чистые металлы без примесей. Верификация модели проводится по экспериментальным профилям скорости свободной поверхности.

2.    Постановка эксперимента

Основным требованием, которое исследователи предъявляют к экспериментам, направленным на количественное описание кинетики образования и развития дефектов, является способность к установлению величин напряжений и деформационной предыстории, особенно локальных, связанных с каждой точкой деформируемого образца. Действительно, высокие растягивающие напряжения при ударно-волновом нагружении генерируются лишь внутри испытуемого образца [2], и невозможно ввести какой-либо датчик, не нарушив целостности образца и не изменив его сопротивление растяжению.

Современная экспериментальная физика ударных волн располагает альтернативными методами измерения кинематических параметров с достаточно высоким временным разрешением. Например, анализ профиля скорости позволяет без дополнительных предположений найти величину растягивающих напряжений, действующих в образце. Наиболее достоверным методом измерения профиля скорости свободной поверхности является метод лазерной интерферометрии, который позволяет проводить бесконтактное (дистанционное) измерение скорости поверхности объектов практически любой природы с высокой точностью. В работе используются данные, полученные с помощью лазерной системы VISAR (Velocity Interferometer System of Any Reflector) [12,13]. В ее основе, как и в других измерительных лазерных системах, лежит эффект Доплера.

3.    Волновые взаимодействия при ударном сжатии

Рассмотрим процесс образования растягивающих напряжений в эксперименте, представляющем собой удар свободно летящей пластиной (ударником) по неподвижной пластине (мишени–образцу) [2] (Рис. 1). Соотношения толщин и диаметров ударника и мишени выбираются так, чтобы обеспечивалась строгая одномерность ударно-волнового процесса в течение всего времени измерений.

В момент соударения на поверхности контакта имеет место скачок массовой скорости — вещество мишени справа от границы покоится, а вещество ударника имеет некоторую начальную скорость в направлении удара. Давление в начальный момент равно нулю по обе стороны границы. В результате соударения образуются две ударные волны, которые распространяются в противоположные стороны — в ударник и в мишень [14]. Очевидно, что ударник при этом тормозится, а вещество мишени приобретает некоторую скорость. Тыльная поверхность мишени является свободной, и, следовательно, давление на ней всегда равно нулю. Поэтому волна, достигнув тыльной поверхности мишени, отражается от нее. Образуется новая, отраженная волна, называемая центрированной волной разрежения, в которой давление, плотность и скорость звука возрастают в направлении распространения волны, а увеличение массовой скорости направлено в обратную сторону [1].

Объектом измерений и анализа являются ударная волна сжатия, следующая за ней волна разрежения, а также волновые взаимодействия при отражении импульса сжатия от свободной (тыльной) поверхности испытуемого образца. Процессы структурных превращений и пластического течения сопряжены с изменением сжимаемости вещества, что в свою очередь проявляется в структуре самих волн сжатия и разрежения. В результате волнового взаимодействия внутри тела генерируются внутренние растягивающие напряжения, которые могут привести к его разрушению.

На рисунке 1 [2] представлена диаграмма «расстояние – время», иллюстрирующая волновые

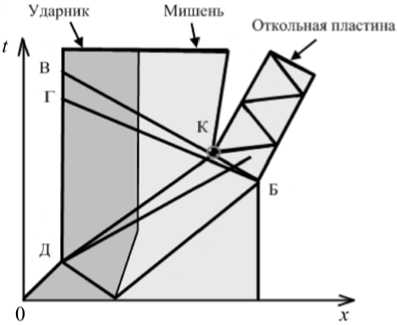
Рис. 1. Схема волновых взаимодействий при ударном нагружении.

взаимодействия при отражении треугольного импульса сжатия ВБГ от свободной поверхности тела, где x — пространственная координата, t — время. В точках Д и Б — точках выхода ударных волн на свободные поверхности ударника и мишени — образуются волны разрежения, распространяющиеся во встречном направлении. В области их взаимодействия напряжения становятся растягивающими. В любой фиксированный момент времени наибольшее растягивающее напряжение достигается на слабом разрыве БKB, а максимальное растягивающее напряжение — в точке K. Растягивающие напряжения вызывают эволюцию дефектной структуры, что ведет к деформированию и возможному разрушению образца.

4.    Математическая постановка задачи

Рассмотрим задачу распространения плоского ударно-волнового фронта умеренной интенсивности (до 5 ГПа) в твердом теле с дефектами. При записи в приближении плоского удара компоненты тензора деформаций е xx * 0 , остальные компоненты равны нулю. Считаем, что поведение ансамблей мезодефектов не выходит за рамки статистической теории [5].

Механизмы пластичности, обусловленные коллективным поведением ансамблей дефектов, рассматриваются в терминах структурных переменных — тензора плотности дефектов и параметра структурного скейлинга. Зарождение дефектов в теле сопровождается деформацией pik , которая называется деформацией, обусловленной дефектами, pk = n S$ik }, где sk — микроскопический тензор, описывающий единичный дефект, n — концентрация дефектов. Рост дефектов в твердом теле сопровождается их взаимодействием и движением, поэтому в материале возникает пластическая деформация. Механизмы пластической деформации связаны с движением дислокаций по плоскостям скольжения. Следовательно, для упруговязкопластической задачи можно ввести три вида деформаций: упругую еe, деформацию p, обусловленную дефектами, и пластическую еp, происходящую вследствие движения дефектов: ее   е  е е = е e+p+еp.                                                (1)

Здесь и далее тензорная величина обозначается буквой со знаком тильда «~». Описание поведения системы начинается с определения термодинамического потенциала [15]. Переменные p и е e отражают реальную структуру материала, следовательно, необходимо подобрать такой потенциал, который можно было бы записать в терминах этих переменных. В работе используется изохорно изотермический потенциал, а именно свободная энергия или энергия Гельмгольца [15].

В процессе деформирования внешняя приложенная работа расходуется на работу пластических деформаций и диссипацию энергии вследствие изменения структуры. Тепловые явления не принимаются во внимание, так как рассматриваемые эффекты проявляются при низких и умеренных нагрузках.

Диссипацию энергии системы, согласно второму началу термодинамики [16], можно записать:

I

ts = 5 ■■е ^p +1 -

d f )    Г д f )

■■ p + -    5> 0, дp J     I д5 J

где T — температура, S — энтропия, 5 — полные напряжения, F — свободная энергия, 5 — параметр структурного скейлинга [5]. Символ « ■■ » означает двойное скалярное умножение, точка над величиной — ее производную по времени.

Следуя принципу Онзагера [16], термодинамические силы могут быть представлены как линейные комбинации термодинамических потоков:

<5 = A 1 s p - A 2 p , д F - Л ~ Л ~ p

--^ = A 313 - A2 8 , дF   л к

--= Л 5 , дз ⁴

A 1 A 3 - A 22 >  0,

• A, . > 0, i = 1"4,

где A ₁, A ₂, A ₃, A ₄ — кинетические коэффициенты, которые в общем случае могут зависеть от всех термодинамических параметров.

Для описания кинетики процесса запишем уравнение движения сплошной среды:

V-d = p й ,                                          (3)

где p — плотность, u — перемещения. Полные напряжения разложим на шаровую ( d o ) и девиаторную ( d _d ) части, так как вклад каждой из этих частей в деформирование различен:

^G = ^d о + ⁶ d .                                              ⁽⁴⁾

Выберем закон Гука в скоростной форме и представим как g = Х 1 1 ( 8 e ) + 2 G s e , где X — первый параметр Ламе, G — второй параметр Ламе (модуль сдвига), 1 1 ( s e) — первый инвариант тензора скорости упругой деформации s e . Учитывая кинематическое соотношение (1), разложение (4) и условие плоского удара s xx = s * 0, получим следующие выражения для соответствующих частей компоненты напряжений, действующей вдоль оси сжатия ст xx = d o + d d (далее величины без знака тильды будут обозначать компоненты соответствующих тензорных величин):

_ Г 2 Л dd = 2G —s-p-sp , d 13            J’(5)

• ⁶ o = K e,

где K — модуль объемной упругости, s — ненулевая компонента полной деформации вдоль оси сжатия.

„                    дdд

Уравнение движения (3) в условиях плоского удара имеет вид: —xx- = p —-. Продифференцируем его дx'81

по координате:

д ² d xx = д V ^ д ² d xx = дв х^ д x ²     ^ д x д t        д x ²     ^ д t ’

где s xx =д V_x /д x , V_x — ненулевая компонента скорости.

Для расчета кинетики пластических деформаций перепишем (2) 1 с учетом (2) 2 :

s

p

A₃         А₂     Г д F ) / "

—---л" + —---I -л^ I /dd 6d

A 1 A 3 ^- A 2 A 1 A 3 ^- A 2 ( ^д p J/ J

здесь выражение в квадратных скобках имеет смысл эффективной вязкости, которая изменяется не только за счет пластического деформирования, но и за счет образования дефектов. Введем в (7) обозначение:

s

p

--------dd .

^T d ^{( d )}

Далее, используя соотношение (2) 2 , с учетом (7), запишем закон кинетики p :

A 2            A 1   f д F 1

C d + tI I .

A 1 A 3 - A 22      A 1 A 3 - A 2 ( д p )

Слагаемое ( -5 F /д p ) отражает изменение свободной энергии за счет образования дефектов. Причем F , как термодинамический потенциал, есть функция параметров модели: F( с , e e , p, 5 ). Тогда (9) можно переписать в виде:

1 f д F 1 ------------------. ^т р ^{( с )} I ^д p )

то есть скорость накопления дефектов пропорциональна скорости освобождения свободной энергии. Теперь систему (2) с учетом уравнений (8) и (10) преобразуем к виду:

e p = —¹— c d , ^т с ^{( с )}

1 f ⁸ F 1 ------------------. ^тр ^{( с )} I ^д p )

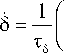
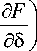
Используя уравнения (4)–(6) и (11) и соответствующие граничные условия, представим систему дифференциальных уравнений, описывающих связь релаксационных механизмов со структурно-скейлинговыми переходами при нагружении мишени в условиях плоского удара, в окончательном безразмерном виде:

^д^_ a_n ae p ²      3^o_ ^{( 1} + ^v)

= -^' T^,              ^e, S = Sd + So, дт дт дт 3 дт   3 (1 - 2v)

дп д ² n _г f д^1 дв = д ² S as p =       д5 f д^1

дт % д^ ^{2 p} ^ дп) , дт дс ² ’ дт ^{с d}, дт ⁵ ( д5 J ’

^Sd L = ⁰,    ^Sd U, = 0, S o L = 0,    S o |^ =с _ирш ( т ),    S o | = 0,

^=1

дп а^м,

I т=0

⁵ ° ,       ^e P |т=0     ⁰,

5=1

Обезразмеривание системы уравнений проводилось с использованием следующих соотношений:

с = 2 G S ,    x = h ^ ,    t = ( h(C_t ) т = т _H т ,    V = C l v , F = F m ^ ,

I      ^тн                   ^f I^е!¹                   I      ^тн

Г = —, Ti т^'ХР -— | i = p, C, Г5 = —, тi                 I Cc )                       т5о где ep — пластическая деформация; Гр, Гс, Г5, % — безразмерные параметры модели; ^ — свободная энергия; Sd — девиаторная и So шаровая части полного напряжения; п — величина деформации, обусловленной дефектами; т — время; ^ — координата; сinput (т) — входящий импульс напряжения; 5 — структурный параметр; v — коэффициент Пуассона; Cl — продольная скорость звука; , _ _ де _ _ h — толщина образца. Обозначение в = — вводится для удобства перехода от гиперболического уравнения к параболическому (е — ненулевая компонента тензора напряжений вдоль оси сжатия). Величины тi (i = p, с, 5) определяют релаксационные свойства материала в процессе нагружения, тр — характерные времена эволюции дефектов, тс определяет релаксационные механизмы, активируемые

-0,04 -0,03 -0,02-0,01 0 0,01 0,02 0,03 0,04 а, Па

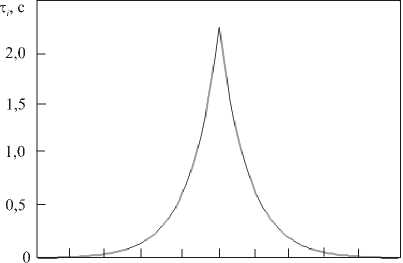
Рис. 2. Зависимость кинетического коэффициента от напряжения

напряжением, и отвечает за пластическую деформацию, т₅ — характерные времена структурных переходов, т i o ( i = p , a , 5 ) — идентифицируемые параметры модели.

В связи с тем, что параметры материала в процессе нагружения меняются, а интенсивность воздействия существенно влияет на отклик, принято решение использовать кинетические коэффициенты т_а и т _p , которые зависят от напряжения (см. (11)). Зависимость т i ( i = p, а ) от а изображена на рисунке 2.

5.    Результаты моделирования

Замкнутая система дифференциальных уравнений в частных производных (12) решалась численно в пакете прикладных программ MATLAB с использованием функции, реализующей алгоритм решения дифференциального уравнения параболического типа. В основе алгоритма лежат метод конечных разностей [17] и многошаговый метод интегрирования по времени с автоматическим выбором шага (метод прогноза-коррекции) [18]. Данный алгоритм является устойчивым и хорошо сходится в задачах со многими переменными, имеющими достаточно разные времена эволюции (например, в задачах, рассматривающих упругие и пластические волновые явления), и имеет первый порядок аппроксимации по координате и не выше пятого порядка аппроксимации по времени.

Для установления параметров модифицированной модели использовалась процедура идентификации, заключающаяся в поиске минимума невязки между расчетной и экспериментальной кривыми деформирования. Постановка задачи оптимизации и метод ее решения (метод прямого поиска) описаны в работе [19], где также найдены константы модели для некоторых металлов (армко-железо, алюминий, медь и другие). На рисунке 3 представлены графики вычисленных зависимостей напряжений от деформаций для ванадия при различных скоростях деформирования. Для сравнения на рисунке приведены экспериментальные кривые из работы [20].

В результате решения задачи оптимизации вычислены следующие кинетические коэффициенты и параметры модели: т _ро = 0,276 с, т_{а о} = 2,22 с, т_{5 о} = 296,5 с, 5 ₀ = 1,96, p c = 0,0228, a c = 0,009. При этом использованы значения упругих констант и плотности ванадия из [21]: Х = 125 ГПа, G = 46 ГПа, р = 6080 кг/м³. Следует отметить, что разработанная модель позволяет описывать диаграммы нагружения при существенно отличающихся скоростях деформирования (например, в данном случае на два порядка) при одном и том же наборе значений констант, что является несомненным преимуществом модели.

Процедура верификации модели проводилась по данным эксперимента с образцом из ванадия в условиях плоского удара. На рисунке 4 представлены результаты численного моделирования и натурного эксперимента (сплошная линия) [21]. Расчетная модель не учитывала разрушение. Скорость свободной поверхности находилась из соотношения v = 2а/ ( р C l ) , где а — напряжение, р — плотность материала, С_l — продольная скорость звука в образце.

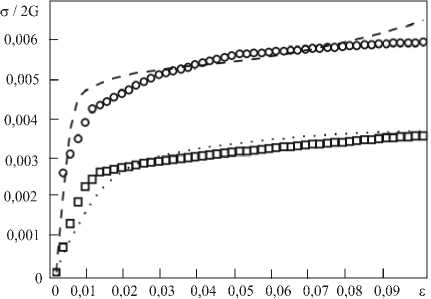
Рис. 3. Экспериментальные кривые деформирования ванадия при скоростях нагружения, [с^-1]: 10^-1(пунктирная линия), 10³(штриховая линия) и расчетные кривые (10^-1 – □, 10³ – ○)

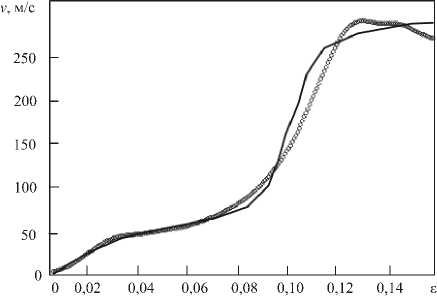
Рис. 4. Волновой профиль для ванадиевого образца толщиной 5,047 мм; ○ – численный расчет, ─ – эксперимент

При моделировании поведения металлов в условиях ударно-волнового нагружения предпринималась попытка описать процесс разрушения. Большинство известных моделей деформирования и разрушения содержат критерии, определяющие условия, при которых начинается макроразрушение [22–25]. Зачастую эти условия не отражают в полной мере явление откола, так как оно зависит от эволюции структуры материала. Введенные в [5] переменные характеризуют дефектную структуру материала, что дает возможность использовать их в формулировке критерия разрушения. Деформация, связанная с дефектами p, — это аналог плотности дефектов, и ее бесконечный рост ведет к макроразрушению. Обнаруженные самоподобные решения автосолитонного типа в виде локализованных обостряющихся мод деформации, обусловленной дефектами, характеризуются как большими значениями в области локализации разрушения, так и большими градиентами [5, 26], поэтому критерий разрушения в модифицированной модели представляет собой произведение величины деформации, обусловленной дефектами, и ее градиента:

p ∇ p ≥ H _c ,

где H _c — критическое значение, соответствующее разрушению.

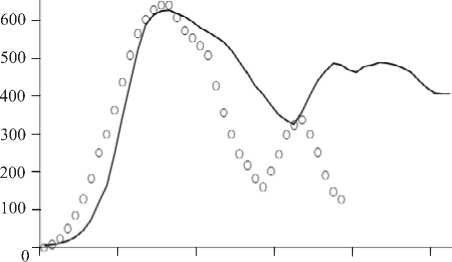
Задача откольного разрушения в условиях плоского удара решена для алюминия. Параметры модели и кинетические коэффициенты были взяты из работы [27], где находились по процедуре идентификации, аналогично описанной в [19]. Численное

1', м/с

0,00     0,07     0,13      0,21      0,24 Л мкс

Рис. 5. Волновой профиль скорости свободной поверхности алюминиевого образца толщиной 2.9 мм, ○ – численный расчет, ─ – эксперимент

моделирование в случае откола проводилось в два этапа: до выполнения условия разрушения расчетной областью был весь образец, затем, в месте интенсивного роста плотности дефектов, когда выполнился критерий (13), сформировалась свободная поверхность, и задача решалась только в отколовшейся части образца. Сравнение экспериментальных [28] и численных данных для откольного разрушения плоского образца алюминия позволяет сделать рисунок 5. Установленный численно профиль скорости свободной поверхности качественно и в какой-то степени количественно соответствует экспериментальным данным. Предложенный критерий позволил установить с точностью до 15–20% область локализации дефектов и скорость их накопления, соответствующие местоположению и моменту откола, что согласуется с экспериментальными данными и говорит о возможности дальнейшего применения этого критерия при моделировании для оценки откольной прочности.

Полученные результаты типичны для деформирования упругопластических материалов. Откольное разрушение при отражении импульса сжатия от свободной поверхности останавливает спад скорости свободной поверхности и формирует так называемый «откольный импульс», повышающий массовую скорость вещества вблизи поверхности разрушения. [2]. Вследствие этого скорость образовавшейся после разрушения свободной поверхности в отколовшейся части увеличивается, и поверхность начинает осциллировать. Волновые профили при ударном сжатии, подобные полученным в рамках данной работы, рассчитывались с помощью численных методов [1–4] и наблюдались в многочисленных опытах [2, 28].

6.    Заключение

Модифицированная математическая модель позволила описать процесс деформирования и разрушения металлов в условиях ударного сжатия. Численно подтверждено, что выбранные два параметра порядка описывают эволюцию дефектной структуры материала в условиях динамического нагружения.

Анализ профилей скорости свободной поверхности показал, что модель адекватно отражает разрушение материала в условиях ударного сжатия, поскольку полученные с ее использованием результаты качественно и количественно соответствуют экспериментальным данным. Предложенный критерий определяет условие, при котором наступает разрушение на уровне структуры, и позволяет установить место и момент зарождения дефектов. Исследование профилей дает возможность определить основные упругие, пластические и прочностные характеристики исследуемого материала.

Работа выполнена при финансовой поддержке РФФИ (проекты № 11-01-96010-р_Урал_а, 11-01-00712-а, 12-01-92002 ННС_а) и Программы Президиума РАН (проекты № 12-П-1-1021, 12-С-1-1013).