Численное моделирование динамического поведения пространственных элементов машиностроительных конструкций

N.A. Shevelev and I.V. Dombrovskiy

Perm State Technical University, Perm, 614600, Russia

For the dynamic analysis of spatial elements of machine-building constructions, new approaches are needed which will take into account such peculiarities of their behavior as the high angular speed of rotation and the significant initial stress caused by temperature gradients, centrifugal loads and element interfacing. The linearized equations of motion have been derived by applying the variational principle. The developed equations describe the influence of the pre-stress state on the dynamic characteristics of elastic systems. The use of three-dimensional relationships essentially improves the accuracy of the results obtained by the theory of plates. Besides, the proposed approach allows us to determine vibration eigenmodes corresponding to the disk motion in the in-plane direction. Numerical results demonstrate that the pre-stress state has a strong effect on the natural vibration frequencies of the system. For real angular speed of rotation, the centrifugal effects lead to an increase (by a factor of 1.5-2) in natural vibration frequencies compared to the steady-state frequency. More complex effects are observed when taking into account the non-uniform temperature field, though its effect on eigenfrequencies is of less significance.

Значительное повышение несущей способности конструкций и жесткие ограничения по весу приводят к тому, что ответственные элементы и узлы работают вблизи предела прочности и устойчивости. Это обстоятельство диктует необходимость использования математических моделей, наиболее полно отражающих поведение реальных объектов, и разработки высокоточных и эффективных алгоритмов расчета. Проблемы оценки динамики и прочности конструкций в полной мере относятся к

проектированию аэрокосмической техники, авиа- и ракетных двигателей, механических накопителей энергии, электрических машин большой мощности, турбомашин.

С точки зрения механики деформируемого твердого тела решение задач статики и динамики для такого рода конструкций связано с формулировкой математической модели для неконсервативной системы, учитывающей весь комплекс механического поведения и, как правило, сложную пространственную конфигурацию реальных объектов.

Наличие больших угловых скоростей в системах приводит к тому, что учёт возникающих при этом дополнительных сил инерции становится необходимым, а изменение жесткости системы за счёт центробежных нагрузок приводит к существенному изменению спектра собственных значений.

Таким образом, для динамического анализа перечисленных выше элементов машиностроительных конструкций требуются нетрадиционные подходы, которые учитывают специфику поведения, например, высокие угловые скорости вращения или значительные начальные напряжения, вызванные температурными градиентами, центробежными нагрузками и конструктивными решениями по сопряжению деталей.

Вариационную постановку задачи запишем, используя принцип возможных перемещений [1] и принцип Даламбера:

δ A σ + δ A u + δ А ц.б. + δ А кор + δ А F = 0. (1)

В выражении (1) слагаемые имеют следующий вид:

∧∧

δ A σ =-   ^GQ ⋅⋅ δε d ν ,

g

S A u = - J p. U ■ S Ud v ,

S A _цб . = - J p to x ( b x ( U + R 0 ) ) ■ S Ud v ,

^А кор = — J 2 p(® x U ) ■ S Ud v ,

^ A F = J F ? ( t ) ■ S UdS,

SF где обозначено: δAσ - работа внутренних напряжений, определяемая возможными перемещениями; δAu - работа сил инерции; δAц .б. - работа центробежных сил; δAкор -слагаемое, определенное силами Кориолиса; δAF - работа внешнего силового возмущения (отсутствует в задачах о свободных колебаниях); Q∧ - энергетический тензор напряжений; δε∧ - вариация тензора деформации Коши-Грина; ν - начальный недеформированный объём; U - вектор перемещений; R0

- вектор, определяющий положение точки в недеформированном объеме; < у - вектор угловой скорости (в данной постановке задачи величина постоянная); ρ - плотность материала конструкции; F - вектор внешнего силового возмущения. Интегрирование ведётся по объёму V , занимаемому упругим телом в трехмерном пространстве, и по поверхности S_F , на которой приложены внешние силовые возмущения.

Искомый вектор перемещений U и его вариация S U должны удовлетворять граничным условиям в перемещениях, а условия в напряжениях выполняются автоматически. Кроме силового внешнего возмущения система может подвергаться кинематическому воздействию, и его учет осуществляется за счет выбора вида вектора перемещений, то есть закладывается в решение.

Вектор перемещений для случая вращающегося упругого тела (свободные колебания) записывается в виде:

U ( r , z , ф , t ) = U ° ( r , z , ф ) + Й ( r , z , ф , t ) ,

где U ° - вектор перемещений, определяющий начальное напряженное состояние; Й - возмущение вектора перемещений относительно некоторого стационарного состояния, подлежащее определению.

Искомый вектор возмущений W можно представить в виде

Й ( r, z, ф , t ) = U ( r, z, ф ) e^p p .

Здесь р - комплексное значение. С учетом (3) вариационная постановка задачи о свободных колебаниях упругих тел с учетом вращения примет вид

А

G ^А                 ^ -            -          ^tJ

I k — Q "Se + р- p ^U + р ( «х ( ю х U ) ) + 2 р ( ю x U ) p ■ 5 U ^ dv = 0, g                                                              J

А

А при этом тензор напряжений Q* соответствует полю перемещений U .

Соотношения (4) далее могут быть использованы для решения следующих задач о свободных колебаниях трехмерных упругих тел:

• а)    свободные колебания трехмерных упругих тел (угловая скорость со равна нулю);

• б)    свободные колебания трехмерных упругих тел с учётом предварительного напряженного состоянии (центробежные нагрузки, температурные градиенты, технологические напряжения и так далее);

• в)    динамическая устойчивость трехмерных упругих тел;

• г)    динамическая устойчивость трехмерных упругих тел с учётом предварительного напряженного состояния.

Во всех перечисленных задачах необходимо определить собственные пары p _к – U _к и, в зависимости от их характера, сделать выводы о динамическом поведении системы. Кроме того, необходимо получить количественные оценки собственного спектра задач б – г по сравнению с классической постановкой задачи о свободных колебаниях (задача а).

Ограничимся на первом этапе постановкой консервативной задачи. Это означает, что в соотношении (1) учитываются только первые два слагаемые:

8 A „ + S A u = 0.                                                          (5)

Тензор деформации е? запишем через линейные тензоры деформации и углов поворота [1]:

Л Л 1

Е = e + —

Л e—

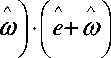
Если искомый вектор перемещений записан в виде (2), то соотношение (6) представляется в виде:

ЛЛ

Е = e °

^Л 1 + e + 2

^ Л Л e °+ e ■

V 7

Л л го° + го

Л л e ° + e

Г

V 7 V 7 V

^ Л Л e °+ e

V7

Л л го+го

^ Л Л

⁺ e ° ⁺ e

V7

^{Л л}

■ ГО + го

V7

Г ' ^Л ^ ^{го +} го

V7

где e ° и ГО — линейные тензоры деформаций и углов поворота, определяемые вектором

Л Л       Л перемещений U °; e и го — линейные тензоры деформаций и углов поворота, определяемые вектором W .

После проведения линеаризации выражения (5) относительно тензоров e, го и учёта работы сил инерции получается вариационное уравнение задачи о свободных колебаниях с учетом предварительного напряженного состояния.

Процедура метода конечных элементов приводит задачу о свободных колебаниях к алгебраической проблеме нахождения собственных значений и собственных векторов { W } вида:

( [ K ] — p ² [ M ] ) { W } = 0,

которая решается методом обратных итераций. Элементы матрицы жесткости [ K ] представляются как

Kj=Kj+Kj, где Kij определяется из решения соответствующей задачи о начальном напряженном состоянии; Kij — элементы обычной матрицы жесткости.

Для исследования влияния на собственные частоты и формы колебаний конструкции разного рода факторов, обуславливающих начальное напряженное состояние, последовательно решены следующие задачи:

• 1.    Задача о свободных колебаниях вращающегося диска наружного радиуса r_A = 0,25 м, толщиной Н = 0,01 м, жестко закрепленного на валу радиуса r _o = 0,02 м, под действием центробежных сил. Одновременно эта задача служила тестом, так как для изгибных форм и соответствующих им частот колебаний имеются литературные данные, полученные с привлечением соотношений теории пластин [2] . Приведенные в настоящей работе результаты являются более полными, поскольку используются уравнения трехмерной теории упругости. Найденные для различных угловых скоростей го первая р 1 и вторая p ₂ собственные частоты колебаний диска и

• Таблица 1. Собственные колебания вращающегося диска

  l	to = 0,0c-1		to = 500c-1		to = 1000c-1		to = 1500c-1
  	p1	p2	p1	p2	p1	p2	p1	p2
  1	776,5	6451	1,19	1,07	1,65	1,18	2,25	1,37
  	830,0	6927	1,19	1,02	1,64	1,07	2,19	1,15
  2	1369	8924,9	1,15	1,03	1,51	1,12	1,97	1,28
  	1406	9297	1,15	1,01	1,50	1,05	1,96	1,13
  3	3103	13087	1,05	1,02	1,19	1,08	1,40	1,17
  	3127	13397	1,05	1,01	1,25	1,04	1,41	1,09
  4	5448	18192	1,03	1,01	1,10	1,05	1,21	1,11
  	5444	18349	1,03	1,01	1,10	1,03	1,22	1,06

• 2.    Задача о влиянии неравномерного нагрева на частоты и формы колебаний диска. Рассмотрены четыре различных температурных режима, взятых из реальной расчетной практики. Конкретный вид режимов характеризуется осесимметричным распределением температуры диска.

результаты работы [2] сведены в таблицу 1 (числитель – данные из [2], знаменатель - авторские результаты). При to = 0 показаны значения приведенных собственных частот, а в следующих позициях таблицы, при to ^ 0, приведены их отношения к соответствующим частотам колебаний при to = 0. Наибольшее влияние состояния проявляется на значениях низших собственных частот колебаний по всем гармоникам l в разложении по угловой координате. Для всех рассмотренных вариантов параметров этим частотам соответствуют изгибные формы колебаний. Поскольку авторами использованы трехмерные соотношения, то оценка форм колебаний и сравнение их с результатами работы [2] проведены по доминирующим компонентам вектора W ={ Wr, Wz, W₽}. Для первой гармоники результаты отличаются приблизительно на 10%, для остальных гармоник это различие снижается до 3, 1 и менее процентов. Собственные частоты, которым соответствуют формы колебаний Wn ={ Wrn,~ 0,Wn} , практически не реагируют на начальное напряженное состояние, что и следовало ожидать.

Последнее замечание играет существенную роль при исследовании устойчивости.

Температурный режим I характеризуется линейным распределением температуры по радиусу

^T ( ^r ) = T ( Г ) ⁺ c ^r .

Температурный режим II представляет собой параболическое изменение температуры по радиусу

T ( r ) = T ( Г о ) + c 2 r ³.

В формулах (10) и (11) приняты обозначения: T(г) - температура диска по окружности радиуса r; T (го) - температура на внутреннем радиусе диска ro; c1 , c2 - константы, определяемые значением перепада температур на наружном и внутреннем контурах диска.

Таблица 2. Собственные колебания неравномерно нагретого диска

	l = 0			l = 1			l = 2			l = 3
	1A т			1A т			1A т			1A T
	80	180	280	80	180	280	80	180	280	80	180	280
I	1,05	1,12	1,16	1,02	1,02	1,02	0,91	0,77	0,60	0,94	0,87	0,78
	1,07	1,16	1,20	1,02	1,03	1,03	0,89	0,72	0,56	0,94	0,85	0,73
II	1,08	1_,_1_7	1,25	1,02	1,03	1,05	0,87	0,69	0,56	0,92	0,81	0,71
III	0,95	0,84	0,73	0,98	0,96	0,93	1,07	1,16	1,25	1,04	1,09	1,14
	0,92	0,80	0,66	0,98	0,96	0,93	1,10	1,21	1,32	1,06	1,13	1,20
IV	0,93	0,82	0,71	0,97	0,92	0,87	1,05	1,11	1,17	1,03	1,06	1,09
	0,95	0,86	0,67	0,98	0,96	0,90	1,06	1,14	1,21	1,03	1,07	1,11

Температурные режимы III и IV позволяют исследовать влияние на частоты собственных колебаний диска отрицательного температурного перепада, то есть такого распределения температур, при котором т ( Га )-T (r )< 0,

где T ( r_A ) - температура на ободе диска.

Аналогично режимам I и II, температурный режим III отличается линейным, а температурный режим IV – параболическим законом изменения температуры по радиусу диска.

Результаты расчетов низшей частоты собственных колебаний диска для температурных режимов I–IV представлены в таблице 2. Здесь l – гармоники в разложении по угловой координате; A T = T ( r_A ) - T ( г . ) ; числитель содержит данные работы [3], в которой использованы соотношения пластин с учетом гипотез Кирхгофа-Лява); в знаменателе приведены результаты авторов.

За счет неравномерного нагрева диска изменяются его динамические характеристики. Так при нагреве диска в центре сильнее, чем на периферии, появляются напряжения сжатия в центральной части и некоторые его собственные частоты, даже без учета изменения модуля упругости материала, падают. Возможна ситуация, когда большой отрицательный градиент температур по радиусу вызовет потерю устойчивости диска, что эквивалентно снижению некоторой собственной частоты до нуля. Смена знака градиента температур вызывает рост собственных частот. Аналогичное действие оказывают и центробежные силы. В реальных условиях температурный и силовой факторы могут присутствовать одновременно, поэтому целесообразны дальнейшие исследования.

Полученные линеаризованные уравнения движения в вариационной форме позволяют учесть влияние предварительного напряженного состояния на динамические характеристики упругих систем. Использование трехмерных соотношений вносит существенное уточнение в результаты, полученные с применением теории пластин.

Использование этой теории для описания динамического поведения тонких дисков приводит к занижению расчётных собственных значений, особенно для низших гармоник. Кроме того, предложенный подход позволяет находить собственные формы колебаний, соответствующие движению в плоскости диска. Для исследования влияния напряженного состояния на собственные частоты эта новая информация о системе не имеет существенного значения, так как изменению подвержены в большей степени изгибные формы колебаний. При рассмотрении вопроса устойчивости этот факт приобретает первостепенное значение. Подробные численные исследования позволяют сделать вывод об ощутимом влиянии предварительного напряженного состояния на собственные частоты колебаний системы. При реальных угловых скоростях вращения центробежные эффекты проявляются в возрастании собственных частот колебаний в полтора-два раза по сравнению со статической частотой. Более сложные эффекты наблюдаются при учете неравномерного температурного поля, хотя его влияние на собственные частоты менее существенно.