Численное моделирование динамики и структуры индуцированного диффузией течения на клине

Под влиянием ряда физических факторов определяющие параметры атмосферы и гидросферы Земли, атмосфер планет и звезд распределены неравномерно. Массовые силы (гравитационные или центробежные) способствуют формированию устойчивой стратификации, задаваемой профилями температуры или концентраций растворенных в жидкости веществ. Такая неравновесная среда с молекулярными потоками стратифицирующих компонент находится в состоянии покоя только в случае, когда градиенты плотности параллельны направлению действия силы тяжести. Возмущения различной природы легко нарушают условия равновесия, создают течения и волны различной природы. Эффекты стратификации активно изучаются и теоретически, и экспериментально.

Исследования последних лет показали, что все доступные для наблюдения природные системы, а также жидкости и газы в лабораторных условиях обладают «тонкой структурой», в которой области со сравнительно медленными изменениями параметров разделяются тонкими границами с областями, имеющими высокие градиенты определяющих физических величин. Особый интерес вызывают

пространственно упорядоченные структуры, обладающие высокой степенью внутренней симметрии. Распространенность таких структур стимулирует поиск механизмов их формирования, среди которых большой интерес вызывают наиболее универсальные, не зависящие от внешних воздействий на устойчиво стратифицированную среду. В этой связи внимание уделяется изучению индуцированных диффузией течений на непроницаемых границах произвольной формы (топографии), вызванных прерыванием молекулярного потока стратифицирующей компоненты.

Первоначальный интерес к данной задаче был связан с поиском механизмов формирования сравнительно тонких горных или долинных ветров в атмосфере [1], которые могут достигать больших значений над ледниками [2], и склоновых потоков в глубоком стратифицированном океане [3]. В дальнейшем сфера приложений результатов исследований индуцированных диффузией течений расширилась и стала включать изучение механизмов самодвижения свободных тел нейтральной плавучести [4], в том числе самодвижение биологических объектов [5, 6]. Первоначально развивалась теория установившихся индуцированных диффузией течений на бесконечной наклонной плоскости в газах [1] и жидкостях [2]. В дальнейшем стали исследоваться физически обоснованные задачи установления течения на плоскости и на пластине конечного размера [7].

В силу сложности задачи расчета течений с учетом эффектов нелинейности в настоящее время в качестве основного инструмента анализа применяется численное моделирование. Современные вычислительные методы позволяют рассчитывать характеристики течения в полной нелинейной постановке и естественных переменных. Однако расчет многомасштабных процессов предъявляет высокие требования к вычислительным ресурсам и кодам. Обычно тонкоструктурные эффекты вносят небольшие поправки в значения динамических характеристик течений. В рассматриваемой задаче возникновение течений обусловлено действием формирующихся градиентов плотности и давления, что существенно влияет на разработку программ расчетов.

Целью данной работы является развитие методик численного моделирования динамики и тонкой структуры стратифицированных жидкостей с учетом их реальных свойств, геометрии расчетной области задачи и влияния внешних динамических факторов на примере задачи формирования индуцированных диффузией течений на клине с прямыми и искривленными гранями.

2.    Уравнения и граничные условия задачи

Базовую математическую модель для изучаемых физических процессов образует система дифференциальных балансных уравнений механики неоднородных многокомпонентных жидкостей в приближении Буссинеска и пренебрежении эффектами сжимаемости, поскольку скорости изучаемых течений малы по сравнению со скоростью звука [8]. Система включает в себя уравнения неразрывности, баланса импульса и вещества с постоянным коэффициентом диффузии и замыкающее алгебраическое уравнение состояния для плотности р ( S ( у ) ) :

div v = 0,

— + ( v V ) v = —— V P + vA v - 5 g , d t              р

v

— + v-V 5 =k,A$ + -,, dt           5 Л

P = Poo (exP (-У/Л) + 5), где S = S0 (у) + 5 — полная соленость, а 5 — ее возмущенная составляющая; р00 — плотность на нулевом уровне у (горизонте нейтральной плавучести); р0 (у) — невозмущенное распределение плотности, которое задается через профиль солености S0 (у); v = (vx, vy) — скорость жидкости, где ось Оу направлена вертикально вверх; P — давление за вычетом гидростатического; v и к5 — коэффициенты кинематической вязкости и диффузии соли; t — время; g — ускорение свободного падения; V и A — операторы Гамильтона и Лапласа; Л = |р0 Дdр0/dy)| — масштаб и N = ^g/Л — частота плавучести.

Постановка задачи предполагает, что в начальный момент времени t = 0 часть покоящейся непрерывно стратифицированной жидкости без возмущений заменяется непроницаемым клиновидным препятствием. На поверхности клина выполняются условия прилипания и непротекания для жидкости, на бесконечном удалении от клина — затухание всех возмущений. Таким образом, физически обоснованные начальные и граничные условия задачи записываются как v, s= 0, v= 0, t≤0                  x, yΣ

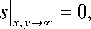
∂ S ∂ n

1 ∂ y +∂ s

Λ∂n  ∂n

где n — внешняя нормаль к поверхности препятствия Σ .

Система уравнений (1), дополненная начальными и граничными условиями (2), самосогласованна и разрешима [8]. Адекватность выбранной математической модели подтверждается соответствием основополагающим принципам механики и согласованностью независимых аналитических, численных и экспериментальных исследований [9–11].

Задача характеризуется набором размерных параметров ( ν= 10 ^{- 6} м²/с, k_s = 1, 41 ⋅ 10 ^{- 9} м²/с, g_y = 9,8 м/с², N = 1 c^-1), которые позволяют задать характерные масштабы времени, скорости и длины [8]. Линейные масштабы геометрической и динамической природы, изменяющиеся в широких пределах, позволяют определить размеры области решения поставленной задачи и степень ее пространственной дискретизации. Макромасштабы Λ и L зависят от ис ходной стратификации и размеров препятствия. Вязкий ( δ^ν _N =ν N = 10 ^{- 3} м) и диффузионный ( δ^κ _N ^S =κ _S/N = 3,75 ⋅ 10 ^{- 5} м) микромасштабы, имеющие диссипативную природу, обуславливают поперечные размеры тонкоструктурных компонент. Достоинство постановки задачи на основе системы (1), (2) — возможность одновременного изучения всех элементов течений в рамках единого описания в естественных физических переменных без привлечения дополнительных констант и связей.

Наряду с фундаментальными уравнениями переноса на практике широко используются теории турбулентности и пограничного слоя. Пренебрежение некоторыми членами в разрешающих уравнениях или введение полуэмпирических замыкающих связей существенно ограничивают сферы применимости данных моделей. К тому же следствием таких операций является потеря симметрии, свойственной системе фундаментальных уравнений [9]. Процедура осреднения физических переменных по Рейнольдсу приводит к сглаживанию тонкой структуры течений.

3.    Численное моделирование

Опыт численного решения задач течений стратифицированных жидкостей методом конечных разностей с помощью собственных программ [7] показал удовлетворительные результаты расчетов на персональных компьютерах. Однако данный подход не получил дальнейшего развития ввиду сложности задачи и необходимости применения высокопроизводительных суперкомпьютерных систем для учета широкого диапазона пространственных и временных масштабов.

В результате анализа коммерческих пакетов прикладных программ с закрытым исходным кодом установлено, что на сегодняшний день нет готовых решений системы фундаментальных уравнений многокомпонентных жидкостей. Заметный прогресс в решении сложных задач механики сплошных сред соотносится с развитием открытых вычислительных технологий, которые позволили реализовать более точные методы построения решений и высокоразрешающие численные модели. Среди свободно распространяемых пакетов одним из наиболее перспективных и быстро развивающихся является пакет OpenFOAM (Open Field Operation and Manipulation). В основе исходного кода лежит набор библиотек, предоставляющих пользователю инструменты для решения ряда прикладных задач, а также распараллеливания расчетов в суперкомпьютерных системах. Численное моделирование стратифицированных течений около неподвижных и равномерно движущихся тел с использованием OpenFOAM показало его хорошую работоспособность [7, 10].

• 3.1.    Расчетная область

Дискретизация расчетной области (построение сетки) производилась в открытой интегрируемой платформе SALOME, которая позволяет создавать и редактировать, импортировать и экспортировать CAD (Computer-Aided Design) модели, строить для них сетки с помощью различных алгоритмов, связывать физические параметры и геометрию рассматриваемой задачи. В подготовке расчетной сетки также участвовали утилиты blockMesh, topoSet и refineMesh пакета OpenFOAM. Основной класс polyMesh строится с использованием минимального объема информации, необходимой для определения элементов и параметров разбиения (вершин, ребер, блоков, внешних границ).

Известно несколько типов расчетных сеток: структурированные и неструктурированные, ортогональные и неортогональные, согласованные и несогласованные с границей области. Каждый тип имеет свои достоинства и недостатки и в значительной степени обуславливает успех построения решения. Метод построения выбирается индивидуально для каждой задачи исходя из значений собственных масштабов и сложности геометрической области.

Неструктурированные сетки, состоящие обычно из треугольников (в двумерном случае) и из тетраэдров (в трехмерном), применимы для областей с произвольной геометрией без ограничений на форму и количество границ расчетной области [12]. Возможность высокой степени автоматизации позволяет существенно сократить временные затраты на построение сеток. Но основной недостаток — нерегулярная структура данных, требует сложных методов численного решения задач математической физики на таких сетках. Использование неструктурированных сеток также усложняет численный алгоритм и нуждается в дополнительной памяти для хранения информации о связях ячеек сетки. К тому же увеличение числа тетраэдральных ячеек по сравнению с числом шестигранных повышает требования к вычислительным ресурсам.

Наиболее эффективными считаются структурированные сетки, согласованные с границами области решения. Они позволяют реализовать вычислительные алгоритмы высокого порядка точности, а также уменьшить продолжительность расчета и необходимый объем оперативной памяти. За счет создания криволинейных сеток можно добиться совпадения сеточных линий с границами области определения функций и тем самым упростить запись граничных условий. Однако, вследствие преобразования координат, в уравнениях, как правило, появляются дополнительные члены. В то же время процедура построения регулярной сетки требует определенных навыков, больших затрат труда и вычислительных ресурсов и применяется только для простых геометрий расчетной области.

При отсутствии возможности нанесения единой сетки на всю расчетную область производится ее разделение на блоки. Сложность реализации такого подхода состоит в выполнении процедуры сшивки решений, полученных в различных подобластях. Тем не менее, метод построения блочноструктурированной расчетной сетки предоставляет широкие возможности для использования эффективных численных методов внутри блоков, в каждом из которых генерируется отдельная сетка регулярной структуры.

Область решения рассматриваемой здесь задачи представляет собой прямоугольник, в центральной части которого расположено клиновидное препятствие длиной L = 0,1 м с высотой основания h = 0,02 м. Расчетная область задачи разделена на семь блоков так, как показано на рисунке 1. Процедура построения ее дискретного аналога была параметризирована, что позволило существенно сократить время перестройки сетки при изменении геометрических характеристик элементов области решения задачи.

Простота геометрии расчетной области позволяет построить блочно-структурированную гексаэдральную расчетную сетку с совмещением линий на границах блоков. В третьем координатном направлении должна быть задана хотя бы одна ячейка, поскольку пакет OpenFOAM, использующий метод конечных объемов для дискретизации системы моделирующих уравнений, воспринимает только трехмерные расчетные сетки.

Тестовые расчеты с различным измельчением расчетной сетки подтвердили необходимость разрешения минимальных микромасштабов задачи. В качестве иллюстрации приводится график зависимости от времени давления вблизи экстремальной вершины клина, где наиболее отчетливо проявляются тонкоструктурные компоненты индуцированных диффузией течений (Рис. 2). Решение становится неустойчивым на грубой сетке 2 с общим числом ячеек 5·105 при минимальном размере ячейки

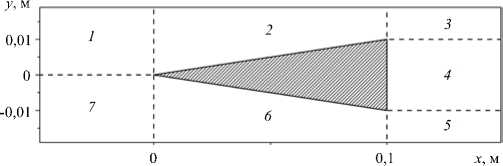
Рис. 1. Схема разбиения расчетной области на блоки

Р, хК/Па

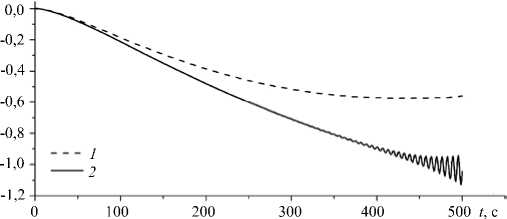
Рис. 2. Эволюция во времени давления в контрольной точке с координатами (0,101;0,011) на сетках с различным минимальным размером ячейки (в метрах) в ее окрестности: кривая 1 – размер ячейки 5·10^-5; кривая 2 – 1,5·10^-4

в окрестности контрольной точки около 1,5∙10^-4м. Для сравнения показано решение на сетке 1 с минимальным размером ячейки 5·10^-5м и числом ячеек 10⁶. Таким образом, для решения даже плоских задач течений непрерывно стратифицированных жидкостей около непроницаемых препятствий требуются высокопроизводительные суперкомпьютерные системы.

Алгоритм разбиения расчетной области предполагает сгущение ячеек в направлении препятствия (см. Рис. 3 а ). Вблизи обтекаемого тела соотношение размеров гексаэдров приблизительно равняется единице, что положительно влияет на сходимость решения. Недостаток такого подхода — измельчение сетки в одной расчетной подобласти, требует построения мелких сеток в других подобластях и влечет за собой излишнюю трату вычислительных ресурсов.

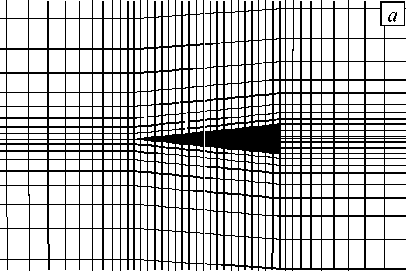
Рис. 3. Схема разбиения расчетной области: с линейным сгущением сетки ( а ), с дополнительным локальным разбиением ( б )

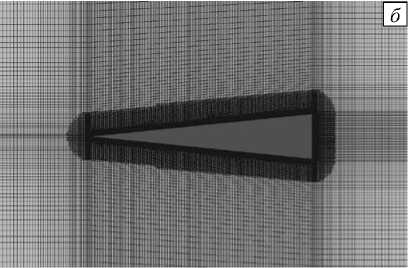
С целью улучшения качества дискретизации расчетной области дополнительно использовались утилиты topoSet и refineMesh, позволяющие на основе геометрических или параметрических признаков выделять интересующие подобласти расчетной сетки и локально измельчать их в соответствии с заданными масштабами и выбранными направлениями (Рис. 3 б ). Минимальный размер ячейки 2,5·10^-5м вблизи непроницаемых границ удовлетворительно разрешает диффузионный микромасштаб δ^κ _N ^S при относительно небольшом общем числе ячеек сетки, равном 4,4·10⁵.

Вместе с тем измельчение пространственного разбиения расчетной области даже на небольшом участке требует соответственного уменьшения шага по времени, что увеличивает продолжительность счета. Существенным недостатком дополнительного локального разбиения является резкое изменение размера сеточных ячеек на границе подобластей, что может отразиться на результатах вычислений. Проверка применяемой расчетной сетки утилитой checkMesh показала ее соответствие набору ограничений, связанных с топологией внешних границ и геометрическими характеристиками ячеек (соотношением размеров, закрученностью, неортогональностью).

• 3.2.    Методика численного моделирования

Численное моделирование системы уравнений движения в пакете OpenFOAM проводится методом конечных объемов в декартовой системе координат. При помощи метода Гаусса интегралы по контрольному объему сводятся к поверхностным, а значение искомой функции на поверхности ячейки получается путем интерполяции ее значений в центроидах соседних ячеек. Открытость исходного кода пакета OpenFOAM позволяет создавать собственные решатели с использованием объектноориентированного языка программирования С++ и строить численные решения для сложных и специфических математических моделей.

Для учета эффектов диффузии в стратифицированных жидкостях был разработан решатель stratifiedFoam на основе стандартного решателя icoFoam, ориентированного на нестационарные уравнения Навье–Стокса для однородной жидкости [10]. В стандартный решатель вводятся дополнительные переменные и соответствующие уравнения для их расчета согласно системе уравнений (1), а также новые вспомогательные параметры: частота и масштаб плавучести, коэффициент диффузии, ускорение свободного падения и другие. Так, в уравнение движения для вертикальной компоненты скорости добавляются члены, учитывающие наличие стратифицирующей примеси, а в уравнение для возмущения солености — дополнительные слагаемые, определяющие фоновую стратификацию.

Интерполяция конвективных членов проводилась по TVD схеме (Total Variation Diminishing), которая вносила минимальную численную диффузию и обеспечивала отсутствие осцилляций решения [13]. На ортогональных участках сетки нормальные градиенты скорости на поверхности ячейки, необходимые при вычислении диффузионных членов по теореме Гаусса, находились из значений скорости в центроидах соседних ячеек по схеме второго порядка. На неортогональных участках применялась итерационная процедура коррекции погрешности, вызванной неортогональностью сетки. Для дискретизации производной по времени прибегали к неявной трехточечной несимметричной схеме второго порядка c разностями назад (backward differencing).

Дискретизация граничных условий (2) осуществлялась с помощью стандартных и расширенных утилит пакета OpenFOAM. Граничное условие возмущения солености было реализовано с помощью расширенной утилиты funkySetBoundaryField, которая позволяет использовать аналитические выражения для различных физических переменных. В файле funkySetBoundaryDict, расположенном в папке system, содержалось выражение переменной s для указанной поверхности. На передней и задней поверхностях, именуемых как frontAndBack, задавалось специальное граничное условие empty. Таким образом, в OpenFOAM исключался расчет плоской задачи в третьем измерении.

Для решения полученной системы линейных алгебраических уравнений применялись итерационные методы сопряженных градиентов с предобусловливанием PCG для симметричных матриц, а для асимметричных матриц — метод бисопряженных градиентов с предобусловливанием PBiCG. В качестве предобусловливателя для симметричных матриц была выбрана процедура DIC, базирующаяся на упрощенной схеме неполной факторизации Холецкого. Для асимметричных матриц, соответственно, запускался предобусловливатель DILU, основанный на упрощенной неполной LU факторизации.

Для связанного расчета полей скорости и давления использовался устойчивый, хорошо сходящийся алгоритм PISO (Pressure Implicit with Splitting of Operators) [14], который показал высокую эффективность в нестационарных задачах. Однако он ограничен по числу Куранта С 0 = u A t/Ах <  1, где и — скорость распространения возмущений, A t — шаг по времени, Ах — пространственный шаг.

Расчеты в поставленной задаче проводились в параллельном режиме с привлечением ресурсов виртуальной вычислительной лаборатории UniHUB (. Декомпозиция расчетной области осуществлялась методом simple. Такой подход допускает наличие высокой пространственной дискретизации расчетной области и проведение более широкого параметрического анализа задач.

4.    Результаты вычислений

Для проведения полного анализа структуры и динамики течений с помощью OpenFOAM можно вычислять новые физические переменные: полную плотность, завихренность, скорость диссипации механической энергии, компоненты тензора вязких напряжений, распределения различных динамических характеристик и другие. Для этих целей предназначены расширенные утилиты funkySetFields, позволяющие задавать аналитические выражения для искомых величин, а также sample, строящая распределения вдоль заданных поверхностей, сечений. Кроме того, утилита sample преобразует поля переменных к различным форматам, что дает возможность обрабатывать результаты вычислений в других пакетах прикладных программ.

Визуализация результатов расчетов, проведенных в открытом пакете OpenFOAM на базе суперкомпьютерных комплексов, выполнялась с использованием графических пакетов ParaView и Origin. Для визуализации скалярных полей применялся высокоразрешающий метод построения полихромных карт изолиний, подобных представленной на рисунке 4 для поля возмущения солености индуцированного диффузией течения около клина. Между изолиниями диапазон изменения величины остается неизменным. Чем гуще изолинии, тем больше градиент изображаемой величины. Информация о структуре поля представляется в виде непрерывного спектра градаций серого цвета. Чем интенсивнее цвет, тем выше абсолютное значение величины в данном диапазоне. В полях положительных значений величин меняются оттенки светло-серого, для отрицательных — оттенки темно-серого цвета. Такой подход позволяет качественно оценивать структуру визуализируемых полей.

Анализ структуры поля давления выявил протяженную область отрицательного давления у острой вершины клиновидного препятствия, а также в тонком слое вдоль его боковых сторон (Рис. 5), к которому примыкает более толстый слой с возмущением другого знака. Разность давлений — подпор у основания и дефицит перед клином, создает интегральную силу, толкающую горизонтальный клин в направлении его вершины.

Интерес представляет влияние на динамику и структуру стратифицированных течений геометрии препятствия, в частности, радиуса и знака кривизны его сторон (их выпуклость и вогнутость). Результаты вычислений поля давления для симметрично искривленного клиновидного тела показали, что размеры области дефицита давления у острой вершины клина зависят от формы искривления боковых сторон. Зона отрицательного давления захватывает часть поверхности вблизи острой вершины

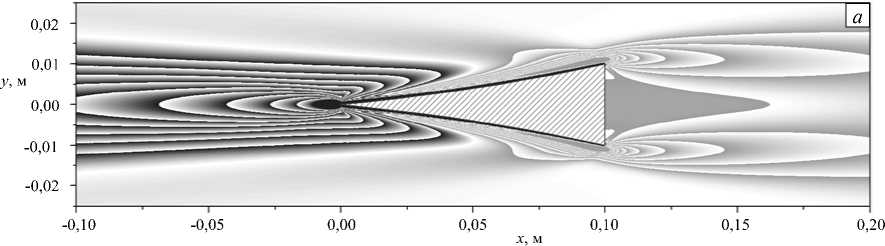
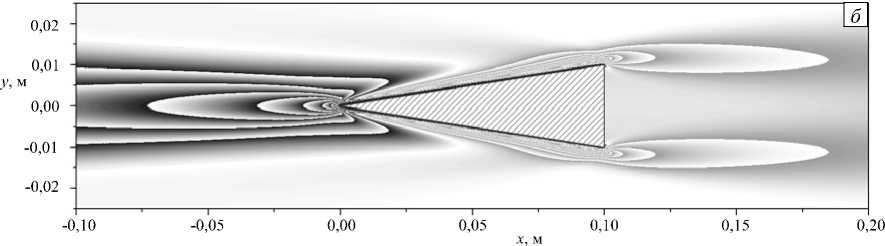
Рис. 5. Поле давления при клиновидном препятствии с вогнутыми ( а ), прямыми ( б ) и выпуклыми ( в ) гранями

клиновидного препятствия с вогнутыми гранями (Рис. 5 а ) и простирается в горизонтальном направлении. При этом толщина зоны значительно больше, чем для выпуклого клина. Картина течения принципиально меняется, если сторону клина изогнуты таким образом, что экстремальная точка смещается от вершины к точке на грани (Рис. 5 в ). Области дефицита давления наблюдаются у всех вершин препятствия, что связывается с изменением наклона кривых граней у вершин препятствия.

Важной представляется количественная информация о распределении давления (Рис. 6). Наибольший дефицит давления наблюдается на стенке клина ( х = 0,0 ^ 0,1 м), при этом интенсивность давления монотонно увеличивается от основания к острой вершине (Рис. 6 а ). Разность давлений порождает пропульсивную силу, приводящую к самодвижению клина. У острых кромок, где наиболее ярко проявляется тонкая структура стратифицированных течений, значения давления резко меняются. Область отрицательного давления простирается далеко вдоль горизонта нейтральной плавучести.

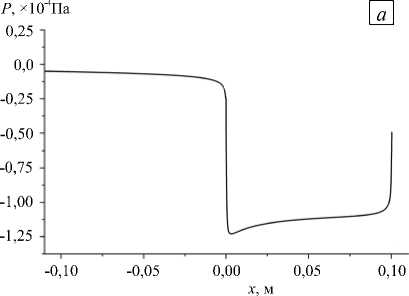
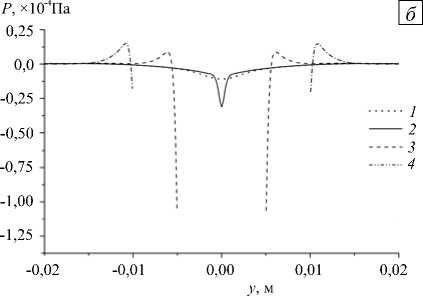
Рис. 6. Распределение давления для клина с прямыми гранями вдоль оси O x ( а ) и в различных сечениях x ( б ): кривая 1 –0,01; 2 – 0,00; 3 – 0,05; 4 – 0,11

Профили давления, приведенные на рисунке 6 б в различных сечениях расчетной области, показывают сложную знакопеременную структуру. Минимальные значения давления зафиксированы на стенке клина. С удалением от стенки его интенсивность резко падает и несколько раз меняет знак, иллюстрируя волновую природу течений, индуцированных диффузией.

5.    Заключение

Разработана методика численного расчета течений в непрерывно стратифицированных жидкостях в открытом пакете OpenFOAM на примере индуцированного диффузией течения на неподвижном клине. Вычисления, проведенные с помощью суперкомпьютерных систем, показали возможность расчета многомасштабных структурированных течений на основе фундаментальной системы уравнений в широком диапазоне параметров задачи.

Из данных расчетов следует, что физическим механизмом самодвижения клина служит разность давлений между областью у его вершины, где дефицит давления возникает вследствие затягивания жидкости в структурированное компенсационное течение, (восходящее) на верхней и (нисходящее) на нижней сторонах, и в областью у его основания.

Важную роль играют краевые эффекты в вершинах углов, образуемых сторонами и основанием клина. Тонкие струйные течения жидкости, формирующиеся вдоль каждой из сторон клина, порождают внутренние волны в областях схождения с угловых точек.

Рассмотренные течения могут использоваться в качестве начальных условий при расчете установления картин обтекания тел внешним потоком.

Работа выполнена при финансовой поддержке РФФИ (проекты № 14-37-50001-мол_нр, 15-01-09235) и программы ОЭММПУ РАН IV-12-4 «Динамика формированияя и взаимодействия волн и вихрей в сплошных средах».