Численное моделирование двумерных газодинамических течений в многокомпонентных неравновесных средах

DOI:

Неравновесные газодинамические течения могут возникать в соплах и камерах сгорания реактивных двигателей (РД) [8; 9; 38; 40], а также при сверхзвуковом обтекании различных аэродинамических и баллистических объектов [21; 22; 37; 39]. Колебательная неравновесность среды, обусловленная различием термодинамической и колебательной температур [10], возникает при интенсивном возбуждении колебательных энергетических уровней молекул как внешними источниками накачки (электрические и СВЧ-разряды, лазерное излучение) [1; 4], так и внутренними физико-химическими процессами в газе (сильные ударные волны при гиперзвуковом обтекании объектов различной формы, интенсивные детонационные волны в РД и ударных трубах, быстрое охлаждение газа при адиабатическом расширении в сверхзвуковых соплах энергетических установок) [2; 12; 22; 39]. В результате такого возбуждения происходит значительное (в несколько или десятки раз) повышение колебательной температуры газа относительно его термодинамической температуры, что приводит к сильному влиянию релаксационных процессов (колебательно-поступательного энергообмена) на структуру газодинамических течений, создавая в неравновесной среде условия для развития новых и усиления известных газодинамических неустойчивостей (акустической, тепловой, тангенциального разрыва скорости течения, резонансных отражательных мод в сверхзвуковых струях) [7; 11; 15–19; 31].

В работах [16; 17] было показано, что на нелинейной стадии эволюции акустической и тепловой неустойчивостей в неравновесном колебательно-возбужденном газе сначала образуется пилообразная система слабых ударных волн (УВ), которая затем распадается на последовательность квазистационарных ударно-волновых импульсов (УВИ). При этом структура слабых УВ определяется параметрами начальных возмущений, а интенсивность УВИ и расстояние между их фронтами зависят только от параметров неравновесной среды, то есть УВИ являются ударными автоволновыми струк- турами [16; 17]. Новые ударно-волновые структуры в [16; 17] были получены с использованием одномерных численных моделей с высоким пространственным разрешением, необходимым для развития акустической неустойчивости и формирования УВИ. Поэтому актуальной задачей является исследование динамики и структуры УВИ в плоских двумерных каналах с таким же высоким разрешением, что требует разработки высокопроизводительных вычислительных инструментов, основанных на параллельных газодинамических алгоритмах для гибридных суперкомпьютеров с графическими процессорами (GPU) [20; 26; 27; 32]. Результаты численного моделирования динамики УВИ в плоских каналах и исследования влияния колебательной неравновесности среды на нелинейную эволюцию газодинамических неустойчивостей в дозвуковых и сверхзвуковых потоках с тангенциальными разрывами скорости течения [15] могут оказаться важными в практических приложениях при разработке РД [8; 9; 38; 40], ударных труб со сложной геометрией [2], газодинамических лазеров (ГДЛ) [1; 12] и экспериментальных энергетических установок [28; 36].

Целью работы является разработка и апробация эффективного вычислительного инструмента, обладающего высоким пространственным разрешением и точностью, для исследования нелинейных волновых структур, формирующихся в дозвуковых и сверхзвуковых неравновесных течениях колебательно-возбужденных газовых смесей на различных стадиях развития газодинамических неустойчивостей (акустической, тепловой, тангенциального разрыва скорости, гофрировочной неустойчивости УВ). Для разработки двумерной вычислительной модели использовался численный метод MUSCL (Monotone Upwind Scheme for Conservation Laws) [25; 44], основанный на приближенных алгоритмах решения задачи Римана о распаде произвольного газодинамического разрыва [24; 42] и адаптированный для учета внешних источников нагрева / охлаждения [41] и интегрирования уравнений динамики неравновесного колебательно-возбужденного газа [16; 17]. Параллельный код численной модели реализован с использованием технологий CUDA и GPUDirect для гибридных вычислительных систем (суперкомпьютеров) с графическими процессорами (CPUs – multi-GPU) [23]. В п. 1 описаны постановка задачи и математическая модель динамики неравновесного газа. Численная модель и параллельная реализация алгоритма представлены в п. 2. Результаты численного моделирования трансзвуковых течений неравновесного колебательно-возбужденного газа приведены в п. 3.

1.    Постановка задачи и математическая модель

Будем рассматривать динамику неравновесной колебательно-возбужденной смеси газов, которая в двумерной области (х,у) характеризуется скоростью течения u = = {u,v}, плотностью q , давлением р, термодинамической Т и колебательной Т у температурами, а также массовой долей химически активных компонентов Y ^ (где к = = 1,...,N _c , а N _c — общее количество компонентов газовой смеси). Газовая смесь может содержать как атомы, так и молекулы химических элементов. Поскольку колебательное возбуждение могут испытывать только молекулы, то введем индекс к ’ = 1,...,N ' , где N '_c — количество многоатомных компонентов газовой смеси N '_c < N _c . В неравновесном колебательно-возбужденном газе Т _у >  Т .

Численное исследование ударно-волновых структур в неравновесном колебательно-возбужденном газе будем проводить в плоском канале длиной L и шириной D с различной конфигурацией течения, зависящей от постановки задачи (см. рис. 1).

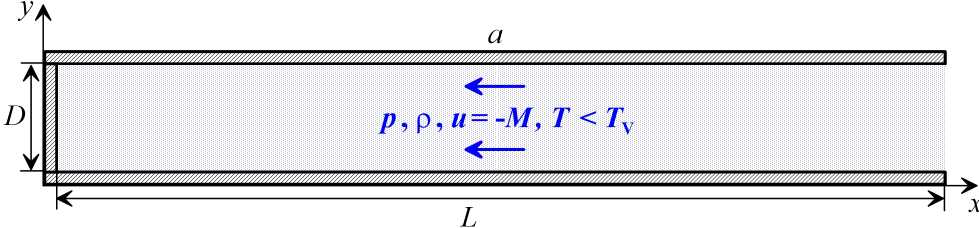
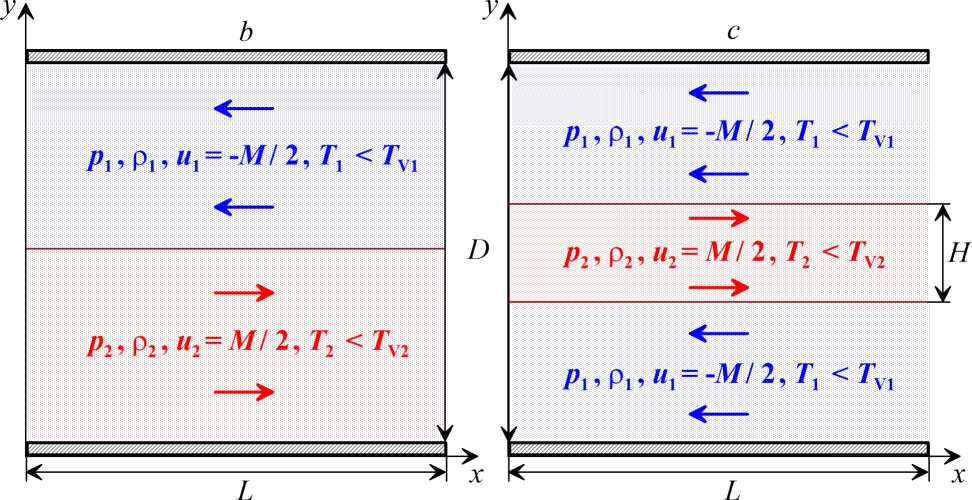
Рис. 1. Общие схемы расчетных моделей плоскопараллельного канала, заполненного неравновесным акустически активным газом: a — задача дозвукового натекания на твердую стенку для исследования структуры УВИ; b — задача с тангенциальным разрывом скорости течения для исследования неустойчивости Кельвина – Гельмгольца; c — задача с двумя тангенциальными разрывами скорости течения для исследования ударно-волновых структур в сверхзвуковых струях. Обозначения: М — число Маха в трансзвуковом потоке; Н — ширина струи; L и D — длина и ширина канала соответственно

В данной работе для апробации численной модели рассмотрены три типа задач:

1)    дозвуковое натекание неравновесного газа на твердую стенку (см. рис. 1a), в результате которого формируются ударно-волновые импульсы, распространяющиеся против потока [18]; 2)    трансзвуковое течение неравновесного газа с тангенциальным разрывом скорости (рис. 1b) для исследования нелинейной стадии развития неустойчивости Кельвина – Гельмгольца (НКГ) в неравновесном газе [15]; 3)    сверхзвуковое течение неравновесного газа с двумя тангенциальными разрывами скорости (рис. 1c) для исследования ударно-волновых структур, формирующихся в сверхзвуковых струях на нелинейной стадии развития газодинамических неустойчивостей [15]; 1. 1. Уравнения динамики неравновесного многокомпонентного газа

Динамику неравновесного многокомпонентного газа с учетом вязкости, теплопроводности, колебательно-поступательной релаксации (VT-релаксация), химических реакций, диффузионного переноса компонентов газовой смеси, нагрева и охлаждения бу- дем описывать следующей системой уравнений газодинамики в консервативной фор- ме [16; 17; 39]:

где

d U d F d G dt dx^ dy

U

*

QU

QV

E

QY _k

\ QYk’ tv,k'/

(             QU             \

QU ² + p - G _xx

QUV - G _xy

(E + p)u — d aV _x T — uo _xx — vo _xy QY k (u — D k V x Y k )

\     QY k ’ E v,k ‘ (u — D k ‘ V xY_k ‘ )     /

(             QV             \

Ф = Q

( 0 \

Q — Л il k ^QQ V,k ‘ ^{— Л} V,k‘ /

QUV — O xy

QV² + p — O yy

(E + p)v — c e V _y T — vo _yy — ua _xy QY k (v — D k V y Y_k )

QY k ’ ^ v,k ‘ (v — D k ’ V y Y k ‘ )     /

E = Q (0.5|v|2 + e); e — удельная внутренняя энергия (поступательные и вращательные степени свободы); Ev,k‘ — удельная колебательная энергия к'-компоненты газовой смеси; oxx, oxy, oyy — компоненты тензора вязких напряжений [6]; ан — коэффи циент теплопроводности; Dk — коэффициент диффузии к-компоненты газовой смеси;

д я t dx’ dy J ^к

V = {V x , V y } =

— удельная скорость химической реакции (образова- ния) к-го компонента газовой смеси. Удельные мощности суммарного энергетического нагрева Q и охлаждения Л газа можно представить в виде:

N'cX.

N _c

Л = Лex + ^Yk (1 — 8r,k^k ,(3)

k=1

где Ev,k‘ — удельная мощность колебательно-поступательного обмена энергией в многоатомных к’-компонентах газовой смеси; Qs — источник внешней энергетической накачки; Hk и cp,k — энтальпия химической реакции и удельная теплоемкость при постоянном давлении к-й компоненты соответственно. Параметры 5s,k и ^R,k определяют долю энергий внешнего источника и химических реакций, которые идут на возбуждение колебательных мод многоатомных компонентов газовой смеси. Величина Лex в (3), связанная с поперечным отводом тепла через стенки канала [16; 17], используется в рассматриваемых задачах для создания начального стационарного состояния. Охлаждение газовых компонент за счет излучения задается функцией Лr,k, а параметр 5r,k определяет долю энергии, которая высвечивается непосредственно с колебательно-возбужденных уровней. Для атомов газовой смеси все параметры bj,k = 0. Величина Qv,k‘ определяет приток / отток колебательной энергии в к'-ю моду за счет колебательно-поступательного обмена, внешних источников и химических реакций, а Лv,k' — лучевой отток энергии из k’-й колебательной моды:

Q v,k ‘ — ^Y k ' (Ё v,k ' + & S,k ' Q s - ^ R,k ‘ H k ‘ R k ‘ ) ,    ^,k ' ^{— Y}k'^rk ^Л г,к ‘ .            ⁽⁴⁾

Систему уравнений (1) замыкаем уравнением состояния идеального газа:

■ ’" (ЕЙ

R         P p мвТ’  е (y- Ш,

-1           Г N и Y — 1 + M Е k=1

Y k

M k (Y k

-

1\

- 1

— молярная масса и показатель

адиабаты газовой смеси соответственно, выраженные через соответствующие величины (M _k и Y _k ) своих компонентов; R — универсальная газовая постоянная. В общем случае показатель адиабаты компонентов газовой смеси зависит от температуры:

(Т ) _—       ^{C p,k (Т} )

^{Y k (} )    c _p,k (Т ) — R/M k

¹ -ЙЕ И

- 1

,

где c _p,_k — удельная теплоемкость при постоянном давлении; в / — коэффициенты полинома, определяющие зависимость c _p,_k (Т ) реальных газов [14].

1. 2. Колебательно-поступательная релаксация и химические реакции Величина Ёу,^ в (2) и (4), определяющая колебательно-диссоциативное взаимодействие в многоатомных к'-компонентах газовой смеси, может быть представлена в виде: Ёv,k‘ — ЁVT,k‘ + eVc,k‘, где ЁVT,k' — описывает процесс колебательно-поступательной релаксации, а ^vc,k' — изменение удельной колебательной энергии из-за химических реакций. Изменение удельной колебательной энергии к'-компоненты газовой смеси в процессе VT-релаксации можно рассчитывать с использованием приближенной формулы Ландау – Теллера [5]: v V,k' £ VT,k' — ---- - Tk‘ Е V,k' , где £.ук' = £ v,k' (Т) — удельная колебательная энергия в равновесном состоянии при Tv — Т; Tk‘ — время колебательной релаксации.

Удельная колебательная энергия к' -компоненты газовой смеси е v,_k ' зависит от соответствующей колебательной температуры Ty, _k ‘ и может быть представлена в виде [16; 17]:

R ^N v^,k ' с VV М ^— м ^ Е

^г l,k ' ^ e,k '

exP (Ql,k' /Tv,k') — 1 , где Nv,k‘ — количество колебательных мод; Q^k' — характеристическая колебательная температура 1-моды; г^^' — степень вырождения 1-моды.

Время колебательной релаксации / ‘ -компоненты газовой смеси при столкновении с молекулами (атомами) /-компоненты можно представить в виде [16; 17]:

.(k) _ к pa exp {££+аг1‘т 1/3+aHT 2/3+аз1‘т 1/3 + h^')- 1]inT} k     Mk‘ Qk‘                        1 — m exp (—0*,k‘/T)

где Qk‘ = oYk‘; pa — атмосферное давление; Q*,k‘ — минимальная из характеристиче- ских температур колебательных мод [3]; калибровочные коэффициенты модели релакса-

( k )         ( k )

ции a lk и n k ‘

вычисляются с использованием полуэмпирических формул [3; 4; 33] или определяются экспериментально [13], бинарный параметр m = (0,1) позволяет в модели включать или отключать поправку кинетической теории [3].

Среднее время релаксации /‘-компоненты газовой смеси из N'c числа многоатомных молекул, имеющих колебательные степени свободы, при столкновении со всеми Nc- компонентами, включая атомы, определяется следующим образом:

T k ‘

=b >  I ‘ k =i ^T k ‘

Для расчета величины изменения удельной колебательной энергии ё vc,_k ‘ восполь-

зуемся моделью [39]:

Е VC,k ‘ = ^ EV,k ‘

( Я k ‘

ID 11 ^{— | R}k‘ | ) ,

которая учитывает только уменьшение колебательной энергии в результате исчезновения молекул / ‘ -компоненты.

Удельная скорость образования /-компоненты в N _r химических реакциях определяется по формуле [39]:

^N r                Г     ^{^c} / y \^{а к}’^{1          Nc} / y \ ^{Ь к}’¹~\

Rk = Mk £(Ь_Ы — а_ы ) /„П^)   — /«П ^J ,     (11)

где a _k,_i и b _k,_i — стехиометрические коэффициенты реагентов и продуктов l-й реакции соответственно, а константы скорости прямой (/ /_;1 ) и обратной (/ _bji ) реакций могут быть представлены в следующем обобщенном виде [39]:

^/ f (b),i = ^A f (_b),i ^T l ^{s ( b ) ,}‘ ^exp ( ^— T± ^ , ⁽¹²⁾

где T _k = T для однотемпературной модели Аррениуса и T _k = у/ TT v,_k для двухтемпературной модели Парка [34]; T_a ,i — температура активации l-й химической реакции; A f(_b),i и B f(_b),i — калибровочные (аппроксимирующие) параметры химических реакций.

1. 3. Коэффициенты вязкости, теплопроводности и диффузии

В многокомпонентном газе коэффициенты вязкости, теплопроводности и диффузии могут быть определены с использованием комбинаторных соотношений [39]:

п Ю

-1

,

д^кУ              V

М     kJ! + м      k      ,

\ y^ ^M k     £^д k ^M k

D _k

=0

-

Mt ^ м V '■

^M k J    k=k ^kk ' ^M k '

Для каждой компоненты газовой смеси коэффициенты динамической вязкости n _k , теплопроводности d_k и бинарной диффузии D _kk ' , полученные в первом приближении теории Чепмена – Энскога [39], могут быть представлены в виде:

n k = с . a' Mf , a e k = C_& ,k У T/M k ,

^D k,k '

= ^Co * ^M/

M k + M k ' M k M k '

f,

где параметры C * ,_k , определенные в работе [39], зависят от температуры a T ^{0 , 15}

• 2.    Численный метод и параллельный CUDA-алгоритм

  2.1.    Двумерная реализация метода MUSCL для многокомпонентного колебательно-возбужденного газа

Для численного решения системы уравнений (1) воспользуемся методом MUSCL [16; 17; 41; 44] и проведем дискретизацию непрерывных величин U (x,y,t) в узлах пространственно-временной сетки: U (x,y,t) м U (x _i ,y j ,t _n ) = U^ , где t _n+1 = t _n + At _n (n = 0,1,... — временной слой); At — временной шаг; x _i+1 = x _i + Ax (i = 0, ...,N _x + 4 — индекс ячейки по х-координате); y j₊₁ = y j + Ay (j = 0, ...,N _y + 4 — индекс ячейки по y-координате); A x = L _x /N _x и Ay = L _y /N _y — размеры пространственных ячеек; L _x и L _y — размеры расчетной области; N _x и N _y — количество расчетных ячеек по хи y-координатам соответственно. Численный консервативный алгоритм метода MUSCL представим в следующем обобщенном виде:

• F^ - F+Jij, + Gj-i/i-Gj^ + фj,(13)

AxAy где дробные индексы i ± 1/2 и j ± 1/2 соответствуют границам ячеек расчетной сетки 1А^

(xi±i/2 = Xi ± Ax/2, yj±i/2 = yj ± Ay/2), Fi±i/2,j = ду       Fi±i/2,j(t)dt, Gij±i/2

• 1     c t++l                     _л           1      r t+₊i

= At J      G i,j ± 1/2 ^(t)dt, ^ф i,j = At~ J      ^ф i,j ^{(t)dt .}

В методе MUSCL второй порядок точности по пространству достигается использо- ванием кусочно-линейной реконструкции сеточных функций в каждой ячейке (xi-1/2 < < х < Xi+1/2, yj-1/2 < y < yj+1/2):

U&y^ n ) = U "j ^{+ (х - х}№^ + ⁽y ^- y j Mj) ,             ⁽¹⁴⁾

где для определения наклонов

/тт" _ TT" TT"   _ TT" \                 /TTn -TTn    TT"   _ TT" \

A^(x) = A( x ) I U ^i,j     U ^{i - 1,j   U i}+^1,j     U ^i,j )      C)( y ) _ A(y ) I U ^ij U ^{i,j - 1}   U ^X¹     U ^ij ]

^id        \    A x     ’     Ax     )'     ^id        \     Ay     , Ay )

могут применяться TVD-ограничители (Total Variation Diminishing) [25; 44]. В работе использовался TVD-ограничитель Ван Лира [25]:

2^2

^ 1 + ^ 2 ^,

0’

^ 1 ^ 2 >  0

^ 1 ^ 2 < 0

Второй порядок точности по времени в методе MUSCL обеспечивается применением процедуры предиктор-корректор. На первом предиктор-этапе вычисляются промежуточные значения параметров течения:

U п + ^{1 /2} _        ^{At n}

^U i,j        ^U i,j ⁺  2

F (удА - ^F (U ? +1 _fiJ) ₊ A x

₊Gjy^v^GJAAf!) Ay

+ Ф (U ”,)

где с учетом (14) имеем U ” ±₁ / ₂ ,j = U ”, ± 0.5 @ ⁽j Ax, U ”j ±₁ / ₂ = U ”, ± 0.5 © ⁽j Ay.

На втором этапе вычисляются величины с использованием приближенных методов решения задачи Римана [24; 42]. При решении задачи Римана о распаде произвольного газодинамического разрыва сначала находим значения параметров течения слева (L) и справа (R) от границ ячеек с учетом (15) и (16):

т т ^(ж) _ т тⁿ + ^1f2 । n 5 (^W д_т

^U L = ^u i ‘ ,j   ^{+ 0.5 H} i ‘ j ^AX ,

^{( ж)} — Ft ” + ^{1 f 2         (}F   д

^U B = ^U i ‘ +1 ,j    ^{0.5 U} i ‘ +1J ^AX ’

^ = f % X = X i ₊ 1 f 2

| г - 1, x = X i — 1 / 2 ’

u L” = U Д² + 0.5 0“‘ Ay, U k^rt = U ”    1 - 0.5 H ” . Ay,

‘ = I j’      y = У , +1 / 2

1 ^{j -} 1’ y = y j - 1/2 .

Затем вычисляем значения потоков на границах ячеек, используя метод Хартена – Лакса – Ван Лира (HLL-метод) [24]:

F i ± 1 / 2 ,j

' Fl ,

S^ F l - sJ^ F b - s j^ ) (u L⁰ - U^)

Q (F   Q(F sB   sL

F b ,

s^ ) >  0

sf ) <  0 < sf )

s J) <  0

В

G i,j ± 1 / 2 = *

GL’ sB”)Gl - sL^Gb - sL”)sB”) (UL”) - U)

⁽” )    A”)

^S b    ^S l

^G B ’

s L” ) >  0

S ( ” ) < 0 < S ( ” )

L         В

s ( ” <  0

В

где Fl = F (uJ0) , Fb = F (W), Gl = G (uj”)), Gb = G (uB”)) , sL^ = min (mJ^ - cj^, «В - c^)) ,       sj”) = min ^xj”) - cj”), x(”) - Сд)) ,

( ^ж )                    ( ^ж )        ( ^ж )     ( ^ж )        ( ^ж )                    ( ” )                    ( ” )        ( ” )    ( ” )        ( ” )

^s B = max + ^c L\ « В ^{+ c} B 4     ^s B = ^max (4 ^{+ c} l ^,x B + ^c B ) ’

( ^(Г     /^(^^/^^"TT^)"                /”)     /4”4Т”44” ⁾"

^c L,B = V ^YL,B Pl,B I ^ L,B ’                  ^c L,B = у ^YL,B Pl,B I ^ L,B .

При численном моделировании тангенциальных разрывов скорости вместо (17) и

(18) лучше использовать HLLC-модификацию для вычисления потоков [42].

(UП + ^{, /}’)

вы-

На заключительном корректор-этапе с учетом (17), (18) и Ф^ = Ф числяем значения параметров течения на tn+1 временном слое по формуле (13).

Численный MUSCL-алгоритм является явным, поэтому временной шаг At _n определяется из условия устойчивости:

N _x ,N _y / At _n = К min i,j =1 \

Ах

Ay     h ²    h²

с П, + K/Cy + Ik, I ’ 2k,' 2,5

' т\,         '

1 w7 nn71  I i,j /

где h = min(Ax, Ay); с = у/yp/q — скорость звука; ^ = п/q — коэффициент кинемати-

′ c /

ческой вязкости; , = &/(qc _p ) — коэффициент температуропроводности; т = min(T _k ‘ ) — к ' =1

Nc минимальное время VT-релаксации; R = max(Rk) — максимальная удельная скорость к=1

химических реакций; К — число Куранта (0 < К <  1).

2.2.    Параллельная CUDA-реализация численного алгоритма MUSCL

Разработка параллельного численного алгоритма MUSCL для гибридных вычислительных систем CPU-multi-GPUs проводилась с использованием технологий OpenMP (уровень CPU — Host), CUDA (уровень GPU — Device) и GPUDirect, который обеспечивает прямой обмен данными между GPUs, минуя Host, с использованием интерфейсов PCI-Express или NVLINK [23; 29; 30].

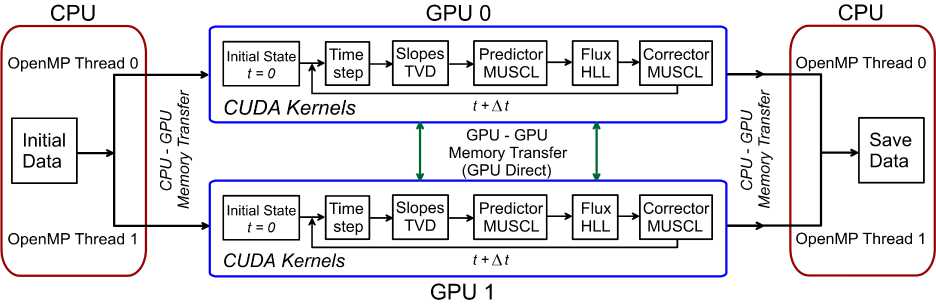
Рис. 2. Потоковая диаграмма параллельного OpenMP – CUDA алгоритма MUSCL для вычислительных систем CPU-multi-GPU

На рисунке 2 представлена потоковая диаграмма, которая демонстрирует принцип организации вычислений на гибридной системе CPU - 2xGPU с использованием параллельных технологий OpenMP – CUDA – GPUDirect. Сначала на уровне Host производится загрузка исходных данных, создаются массивы для величин численного алгоритма и проводится декомпозиция расчетной области с учетом используемого в вычислениях количества GPU. Для случая, показанного на рисунке 2, в результате декомпозиции создаются две подобласти, которые будут рассчитываться на отдельных GPU. Далее с использованием OpenMP на уровне Host (CPU) создаются два параллельных потока (OpenMP Threads), которые обеспечивают параллельную загрузку данных и запуск CUDA-ядер (CUDA Kernels) численного алгоритма MUSCL на двух GPU (GPU 0 и GPU 1).

В процессе выполнения расчетов между GPU осуществляется обмен данными с использованием GPUDirect, необходимый для синхронизации вычислений. После совершения заданного количества итераций (временных шагов) расчетные данные выгружаются обратно на CPU (Host). Основные CUDA-ядра численного алгоритма MUSCL:

• •    «Initial State» — создает начальную конфигурацию газодинамического течения;

• •    «Time Step» — вычисляет временной шаг по формуле (19);

• •    «Slopes TVD» — определяет наклоны (@(^x), @^(x)) кусочно-линейной реконструкции сеточных функций (14) с использованием TVD-ограничителя (15);

• •    «Predictor MUSCL» — рассчитывает промежуточные значения сеточных функций UH+1/2 на предиктор-этапе метода MUSCL по формуле (16);

• •    «Flux HLL» — вычисляет плотности потоков (F, G) консервативных величин на границах ячеек (^±1/2, Уз±1/₂} с использованием HLL-метода (17) и (18);

• •    «Corrector MUSCL» — рассчитывает новое состояние величин Uⁿ⁺¹на следующем t_n+1 временном слое по формуле (13).

3.    Результаты численного моделирования 3.1.    Ударно-волновые импульсы в плоском двумерном канале акустически активного неравновесного газа

Результаты численного моделирования удобно анализировать в безразмерном виде [17], переходя в исходных уравнениях математической модели (п. 1) к безразмерным величинам f = f/l f , где I f — соответствующие характерные масштабы численной модели (п. 2): l _t = Т о ; l _u = С о ; l _xy = С о т о ; l _T = Т о ; l _p = р о ; l _e = ^ q / y o - Нижний индекс «0» соответствует начальным пространственно однородным распределениям газа.

Для численных моделей выберем высокое пространственное разрешение c Ах = = Ау = 0.01, которое позволяет исследовать нелинейную динамику газодинамических неустойчивостей в неравновесном газе (см.: [16–19]).

Определим базовые фиксированные значения параметров численных моделей в соответствии с [17]: у = 1,4; Т _ех = 0, 3; а о = у о = 10 ^{- 4} ; а 1 = 10; а ₂ = а ₃ = п = m = 0; Y₃ = 0. Для всех трех задач (см. рис. 1) будем использовать следующие начальные распределения давления, температуры и плотности: р ₀ = Т _о = 1 и а ₀ = у.

Для исследования структуры ударно-волновых импульсов, формирующихся в плоском канале при дозвуковом (а = М _о = - 0,5) натекании неравновесного колебательно-возбужденного газа (Т у ₀ ~ 3,104) на твердую стенку (см. рис. 1 a ), рассмотрим каналы с фиксированной длиной L = 204,8 и различной шириной: D 1 = 0,64, D 2 = 1,28, D 3 = 2,56, D 4 = 5,12. С учетом выбранного пространственного разрешения количество расчетных ячеек по х и у координатам составляет N _x = 20 480 и N _y = { 64, 128, 256, 512 } соответственно.

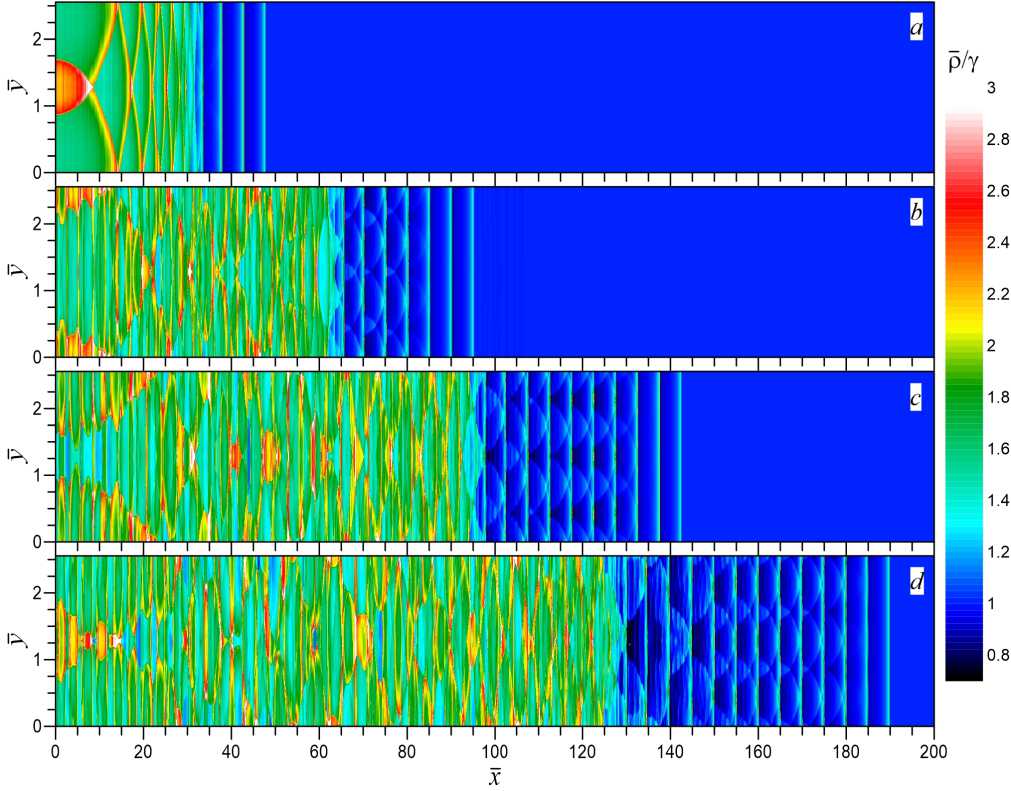
Рис. 3. Динамика ударно-волновых импульсов в плоском канале неравновесного газа. Показаны распределения плотности в различные моменты времени: a — t = 50 ; b — t = 100 ; c — t = 150 ;

d — 1 = 200

В этой численной модели на левой, нижней и верхней границах расчетной области задаются граничные условия типа «твердая стенка» с условиями непротекания и прилипания. На правой границе газ втекает в расчетную область с дозвуковой скоростью. Для создания начальных возмущений в поперечном основному потоку направлении (по /-координате) в окрестности левой границы задаем значение //-компоненты скорости в виде:

У = А- exp (-) 2- £ sin /^ , где Av — безразмерная амплитуда возмущений скорости; величина mv = Ny/16 определяет количество гармоник возмущения, самая коротковолновая из которых моделируется 16-ю расчетными ячейками. В качестве базовых значений численной модели выберем Av = 0,01 и 5 = 1.

Процессы формирования и распространения ударно-волновых импульсов в плоском канале (D ₂ ) акустически активного неравновесного газа показаны на рисунке 3. При взаимодействии набегающего потока с твердой стенкой возникают возмущения [18], которые из-за развития акустической неустойчивости нарастают до нелинейных амплитуд и образуют слабые ударные волны. Эти слабые УВ в неравновесном акустически активном газе оказываются неустойчивыми и быстро распадаются на последовательность ударных

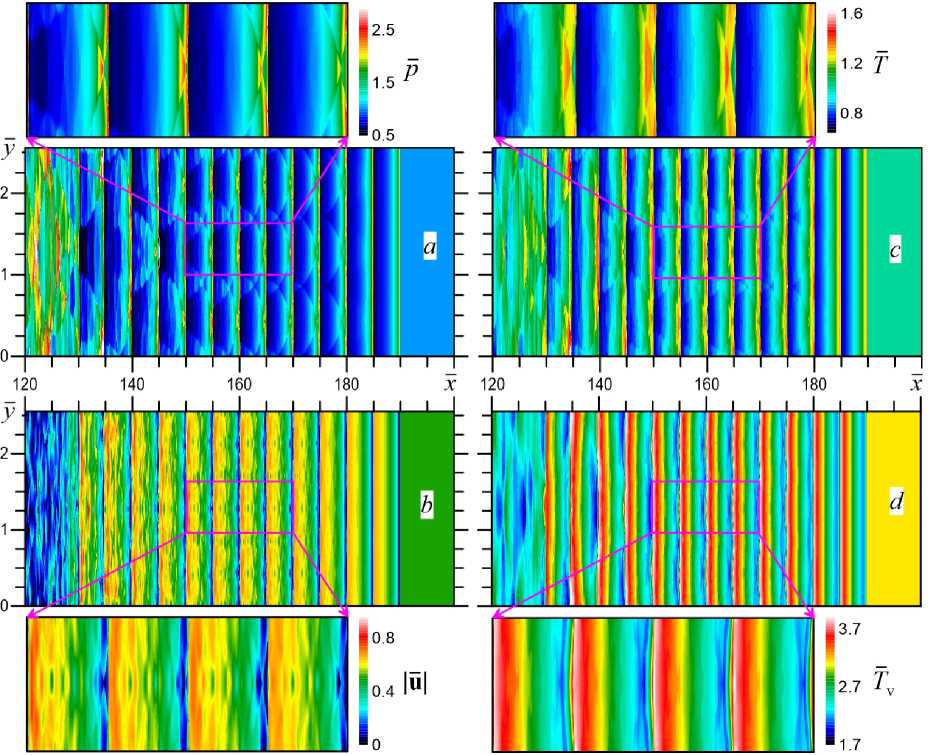
Рис. 4. Ударно-волновая структура течения в плоском канале неравновесного газа. В момент времени t = 200 показаны распределения: a — давления; b — модуля скорости; c — температуры; d — колебательной температуры автоволновых импульсов [16; 31]. Поскольку амплитуда возмущений х-компоненты скорости (и) существенно больше, чем возмущения ^-компоненты скорости (у), то сначала образуются 2–3 УВИ с плоским фронтом (см. рис. 3a). Затем начинают формироваться последующие УВИ, но уже с хорошо заметным неоднородным распределением параметров течения по ^-координате (см. рис. 3b, c, d). Поперечная неоднородность структуры течения как в ударно-волновых импульсах, так и в области торможения газа (между твердой стенкой и последовательностью УВИ) связана с нарастанием амплитуды косых возмущений из-за развития акустической неустойчивости. Эти косые возмущения также приводят к образованию в области торможения газа косых ударных волн, которые, многократно отражаясь от стенок канала, формируют в этой области к моменту времени t = 200 сложную нерегулярную структуру течения (см. рис. 3d).

На рисунке 4 показана более детальная структура течения в системе ударноволновых импульсов, формирующихся в плоском канале (D 2 ) к моменту времени t = = 200. В распределениях давления (рис. 4 a ) и температуры (рис. 4 c ) хорошо видны локальные максимумы на фронте УВИ, которые образуются из-за нарастания наиболее неустойчивых отражательных (поперечных) гармоник акустических колебаний с длиной волны Л * ~ 1. По распределению модуля скорости на рисунке 4 b можно сделать вывод о

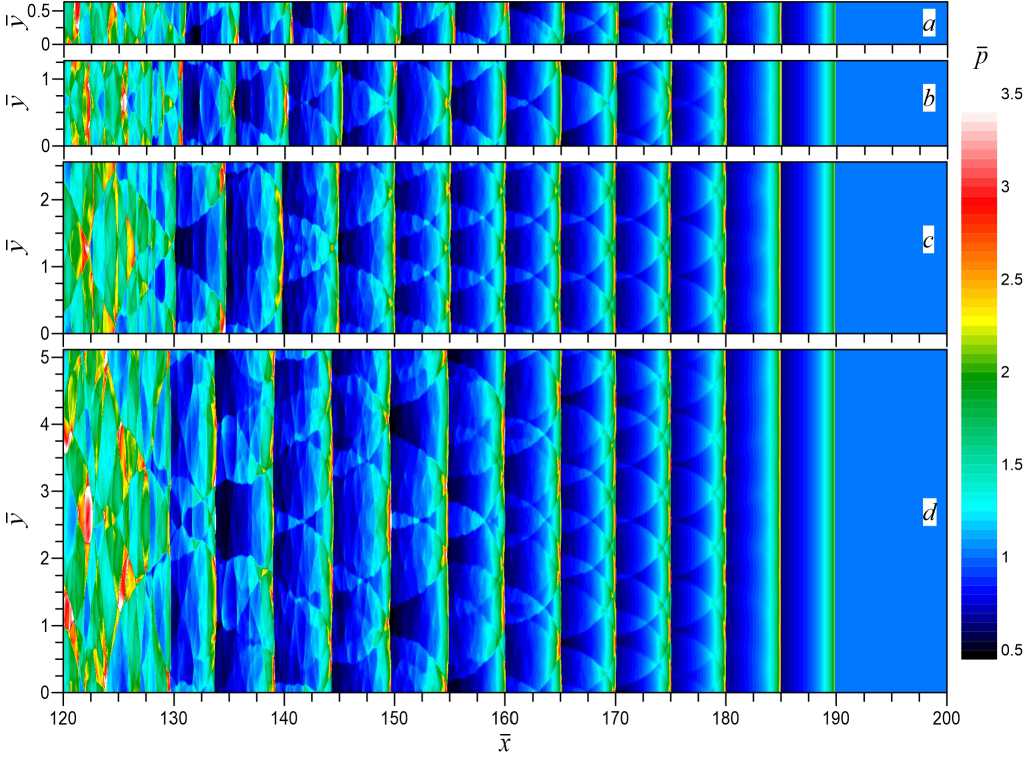
Рис. 5. Ударно-волновая структура течения в плоском канале неравновесного газа. В момент времени t = 200 показаны распределения давления ( р ) при различных значениях ширины канала: a — D 1 ; b — D 2 ; c — D 3 ; d — D 4

том, что за фронтом УВИ, начиная с 4–5 УВИ и далее влево, происходит турбулизация потока из-за развития акустической неустойчивости мелкомасштабных гармоник. Для более детального описания перехода от ламинарного течения к турбулентному необходимо либо увеличивать пространственное разрешение численной модели (13) на несколько порядков и рассматривать трехмерные течения в рамках DNS-подхода, либо переходить к моделям турбулентности RANS/LES [35; 43]. По распределению колебательной температуры на рисунке 4 d хорошо заметна изгибная деформация фронта ударно-волновых импульсов и областей заударного течения.

На рисунке 5 продемонстрирована зависимость структуры течения от ширины канала (D) в области формирования последовательности ударно-волновых импульсов (120 < х <  200). С увеличением ширины канала возрастает и количество локальных максимумов на фронте УВИ, связанных, как было отмечено выше, с развитием акустической неустойчивости отражательных гармоник с λ _* .

Реализованный в работе параллельный алгоритм (OpenMP – CUDA – GPUDirect) метода MUSCL для гибридных суперкомпьютеров с графическими процессорами (GPUs) позволил сократить вычислительное время в сотни раз по сравнению с версиями кода для CPUs. В таблице представлено вычислительное время выполнения одного итерационного шага для параллельного CUDA-алгоритма MUSCL при расчетах на GPU NVIDIA TESLA V100 в зависимости от общего количества расчетных ячеек (N = N _x х N _y ) в численных моделях с различной шириной канала. Сравнение этого вычислительного

Зависимость времени выполнения одного итерационного шага (t _apu ) от числа расчетных ячеек ( V ), полученных на multi-GPU NVIDIA TESLA V100

	t GPU , мс
V	I x GPU	2 x GPU	4 x GPU	Модель
1 310 720	2,7	1,50	0,84	D i
2 621 440	5,02	2,73	1,55	D 2
5 242 880	9,78	5,20	2,98	D 3
10 485 760	19,03	10,02	5,73	D 4

3.2.    Влияние неравновесности среды на динамику неустойчивости Кельвина — Гельмгольца

Исследуем влияние неравновесности среды на устойчивость сдвиговых течений колебательно-возбужденного газа. Для этого рассмотрим плоский канал с фиксированной длиной и шириной L — D — 10, 24, расчетная область которого имеет следующие размеры: 0 < х <  10,24 и - 5,12 <  у <  5,12. С учетом выбранного пространственного разрешения численных моделей (Ах — Лу — 0,01) количество расчетных ячеек по х- и у-координатам составит: N _x — N _y — 1 024. На левой и правой границах расчетной области ставятся периодические граничные условия, а на верхней и нижней границах — условия непротекания. Начальное распределение скорости течения по х-координате внутри этого канала представим в виде:

Мо      у ио(х,у) ——tanh - = , где Мо — число Маха на тангенциальном разрыве скорости; h — характерная длина сглаживания разрыва, которая определяет ширину переходного слоя — 4h. В качестве базового значения выберем h — 0, 02.

Для создания начальных возмущений на границе раздела двух сдвиговых потоков газа зададим у-компоненту скорости в виде:

^— A , exp (-К0 - f sin (²ⁿ’_i) .

В качестве базовых значений выберем A , — 0.01 и т , — N ^ /16.

В рамках линейного анализа устойчивости в работе [15] было показано, что нерав-новесность среды (Ту > Т) приводит к увеличению инкремента неустойчивости Кельвина – Гельмгольца (НКГ) для трансзвуковых сдвиговых течений из-за акустической активности колебательно-возбужденного газа. В связи с этим возникает задача об исследовании влияния неравновесности среды на волновые структуры, формирующиеся на нелинейной стадии развития неустойчивости Кельвина — Гельмгольца. Для решения этой задачи была проведена серия вычислительных экспериментов с различными значениями параметров численной модели тангенциального разрыва скорости (М0, Tv0, h, Л).

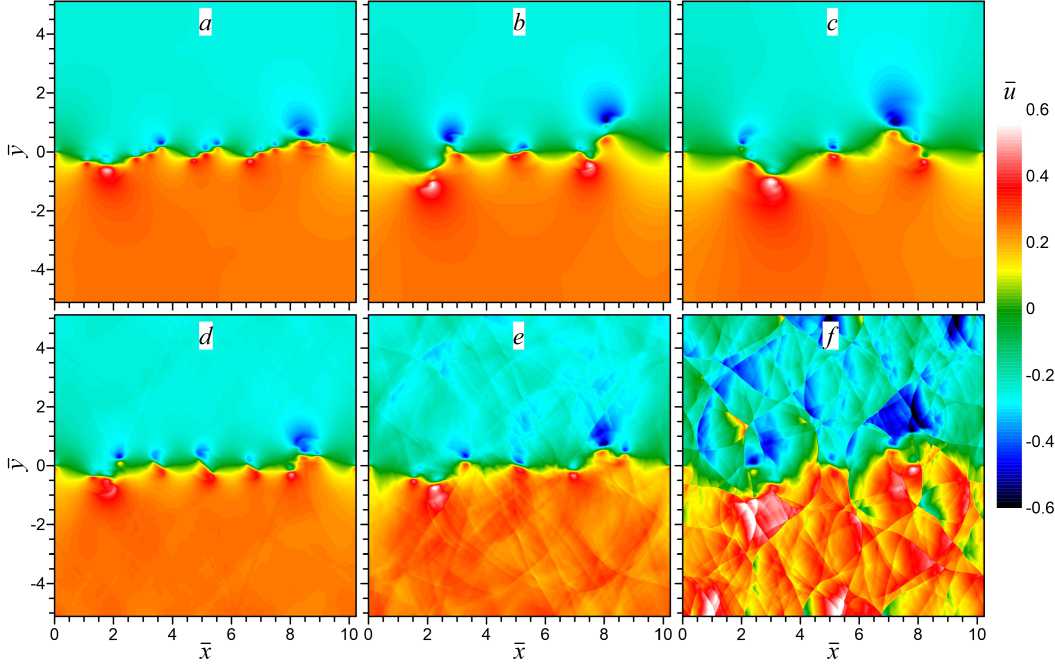
Рис. 6. Нелинейная динамика неустойчивости Кельвина — Гельмгольца в равновесной среде (верхняя панель — a , b , c ) и неравновесном колебательно-возбужденном газе (нижняя панель — d , e , f ) при М 0 = 0 , 5 . Показаны распределения д-компоненты скорости течения в различные моменты времени: а и d — t = 20 ; b и e — t = 25 ; c и f — t = 30

На рисунках 6 и 7 представлены результаты численного моделирования нелинейной динамики неустойчивости Кельвина — Гельмгольца в равновесном (T _v0 = T 0 = 1) и колебательно-возбужденном (T _v 0 ~ 3,104) газах при различных значениях числа Маха (М 0 = { 0, 5; 1 } ) и фиксированных параметрах h и A _v , соответствующих базовым значениям.

Сравнение нелинейной стадии развития неустойчивости Кельвина — Гельмгольца для дозвукового тангенциального разрыва (М ₀ = 0, 5) в равновесной среде (T _v = T ) и в неравновесном колебательно-возбужденном газе (T _v >  T ) показано на рисунке 6. Учет неравновесности среды приводит к усилению неустойчивости Кельвина — Гельмгольца, более интенсивным деформациям границы раздела встречных (сдвиговых) потоков и ускорению образования соответствующих вихревых структур, характерных для нелинейной стадии эволюции НКГ (рис. 6 а , d ). К моменту времени t = 25 в неравновесном газе наряду с классическими вихревыми структурами формируются слабые ударные волны из-за развития акустической неустойчивости (рис. 6 b , e ). Эти слабые УВ к моменту времени t = 30 эволюционируют в более интенсивные ударно-волновые импульсы (подп. 3.1), которые, многократно отражаясь от стенок канала, формируют

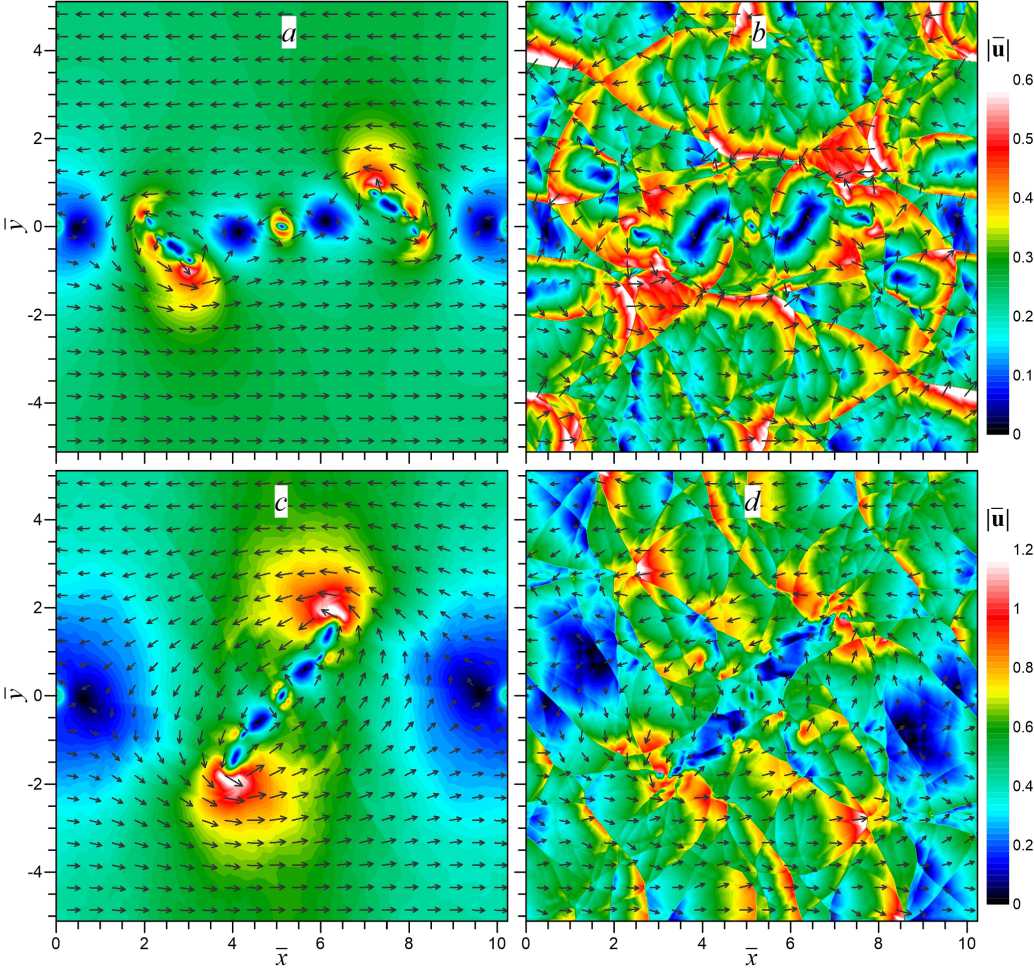
Рис. 7. Вихревая и ударно-волновая структура течения на нелинейной стадии развития неустойчивости Кельвина — Гельмгольца в равновесной среде ( a , c )

и в колебательно-возбужденном газе ( b , d ). Показаны распределения модуля скорости течения

|u| для различных чисел Маха и моментов времени: a , b ( верхняя панель) — М 0 = 0 , 5 и t = 30 ; c , d ( нижняя панель ) — М 0 = 1 и t = 25

сложную ударно-волновую структуру течения (рис. 6 c , f ). Дальнейшая эволюция вихревых и ударно-волновых структур в неравновесном газе приводит к более интенсивному и быстрому перемешиванию встречных потоков по сравнению с равновесной средой, формируя нерегулярную (турбулентную) структуру течения.

Сравнение детальной вихревой и ударно-волновой структуры течения на нелинейной стадии развития неустойчивости Кельвина — Гельмгольца в равновесной и неравновесной средах при различных значениях числа Маха (М 0 = { 0, 5; 1 } ) показано на рисунке 7. Для равновесного газа в центре расчетной области хорошо заметны характерные вихревые структуры типа «кошачий глаз», образующиеся на нелинейной стадии развития НКГ (рис. 7 a , c ). В неравновесном колебательно-возбужденном газе даже на дозвуковых и околозвуковых режимах течения наряду с вихревыми структурами образуется сложная система ударных волн, что в результате приводит к формированию единой ударно-вихревой структуры течения (рис. 7 b , d ). С ростом числа Маха увеличивается интенсивность и скорость образования таких ударно-вихревых структур в неравновесной среде.

3.3.    Ударно-волновые структуры в сверхзвуковых струях неравновесного газа

Поставим задачу об исследовании ударно-волновых структур, возникающих в сверхзвуковых струйных течениях неравновесного-колебательно-возбужденного газа из-за развития газодинамических неустойчивостей. Ранее в работе [15] на основе линейной модели было показано, что неравновесность среды усиливает неустойчивость как поверхностных мод (НКГ), так и отражательных гармоник симметричных и антисимметричных мод струи. Рассмотрим такой же плоский канал, как и в подп. 3.2 (те же размеры, граничные условия и количество расчетных ячеек), но поместим в его середине плоскую струю шириной Н, истекающую между двумя параллельными тангенциальными разрывами скорости вдоль канала. Границы струи располагаются симметрично относительно оси (у = 0) на расстояниях ± Н/2.

Начальное распределение скорости течения по х-координате внутри плоского канала со струей посередине представим в виде:

М о и о^ у ) = —

tanh

(У

— tanh

(У

-

времени со временем выполнения параллельного OpenMP-кода на CPU (2 x IntelXeon E5-2698v4) с 40 физическими ядрами дает следующую оценку ускорения вычислений

на GPU V100:

с     _ tCPU

^ 4 x GPU ^— ---- ^t GPU

S i x G PU —

—--

5, 73

t CPU ^ GPU

- 595.

—

³⁴⁰⁸     _{7 c}       _ ^tCPU

— 179, ^2x0 pu — ---- —

19,03        ’ 2^xGPU     t GPU

3408 ----- — 340, 10, 02

где у ± = у ± Н/2. В качестве базовых значений выберем Н = 2 и h = 0, 02.

Для создания начальных возмущений на границах струи зададим у-компоненту скорости в виде:

М",У) = B _v

Г ( У- V < У- ^1 1 \Г • (2nj Л [exp I-d +exp ^ h-) J ^gsin l т "J, где Bv = Av sign(y) для симметричных мод струи (S-мода, или пинч-мода) и Bv = Av для антисимметричных мод струи (AS-мода или изгибная мода). В качестве базовых значений также выберем Av = 0, 01 и mv = Nx/16.

Для решения поставленной задачи об исследовании ударно-волновых структур в сверхзвуковых струях была проведена серия вычислительных экспериментов с различными значениями параметров численной модели (М _о , Т у 0 , h, A _v , Н ).

На рисунках 8 и 9 представлены результаты численного моделирования нелинейной динамики неустойчивых S -мод струи в равновесной среде (Т у 0 = Т _о = 1) и колебательно-возбужденном газе (Т у 0 ~ 3,104) при М _о = 4 и фиксированных параметрах h, A _v и Н , соответствующих базовым значениям.

Сравнение ударно-волновых структур, формирующихся на нелинейной стадии развития газодинамических неустойчивостей в сверхзвуковых струях равновесного и неравновесного газов, показано на рисунке 8. Одна из газодинамических неустойчивостей, развивающихся в равновесных и неравновесных средах между двумя тангенциальными разрывами скорости сверхзвукового струйного течения, это неустойчивость Кельвина – Гельмгольца [15], которая на нелинейной стадии эволюции приводит к образованию вихревых структур (см. подп. 3.2) в окрестности границ струи. Эта неустойчивость является поверхностной, поскольку развивается вблизи границ струи, деформируя ее поверхность (см. рис. 8 a , b , d ). Вместе с НКГ в сверхзвуковой струе неустойчивыми оказываются отражательные гармоники звуковых волн, которые в равновесном газе нарастают благодаря эффекту сверхотражения от границ струи, а в неравновесной среде скорость нарастания этих гармоник дополнительно увеличивается за счет развития акустической неустойчивости колебательно-возбужденного газа [15]. На нелинейной стадии

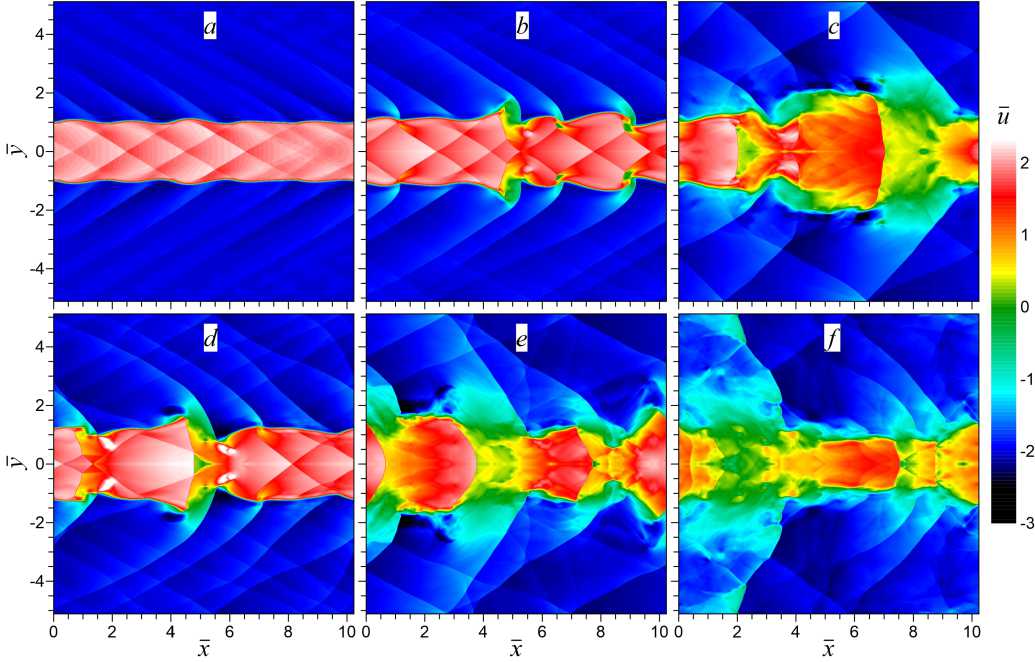
Рис. 8. Эволюция газодинамических неустойчивостей в сверхзвуковых струях равновесного ( верхняя панель — a , b , c ) и колебательно-возбужденного

( нижняя панель — d, e , f ) газов при М 0 = 4 . Показаны распределения ^-компоненты скорости течения в различные моменты времени: а и d — t = 15 ; b и e — t =18 ; c и f — t = 23

эволюции неустойчивые отражательные моды образуют систему косых ударных волн как внутри струи, так и во внешней среде (см. рис. 8 a , b , d ). Совместное действие этих двух типов неустойчивостей приводит к формированию характерных ударно-волновых структур — конусов и дисков Маха, наблюдаемых в реальных цилиндрических сверхзвуковых струях. Плоский аналог этих ударно-волновых структур можно выделить и на рисунке 8. Дальнейшая эволюция ударно-вихревых структур, образовавшихся в сверхзвуковой струе на нелинейной стадии развития рассмотренных выше газодинамических неустойчивостей, приводит к торможению струи из-за УВ, движущихся против потока, и в конечном итоге струя разрушается в результате ее распада на отдельные сгустки, интенсивного перемешивания и турбулизации встречных потоков газа (рис. 8 c , e , f ). Как и в случае одного тангенциального разрыва скорости течения (см. пп. 3.2), учет нерав-новесности среды приводит также к усилению неустойчивых мод струи (НКГ, S -моды), формируя на нелинейной стадии их развития более интенсивные ударно-вихревые структуры, которые ускоряют эволюцию и распад струи, а также увеличивают турбулентность в потоке колебательно-возбужденного газа (см. рис. 8, верхняя и нижняя панели).

На рисунке 9 показана более детальная ударно-вихревая структура течения, формирующаяся в сверхзвуковой струе неравновесного колебательно-возбужденного газа к моменту времени t = 18 и соответствующая распределению скорости и на рисунке 8 e . По распределениям давления, температуры и модуля скорости на этом рисунке хорошо выделяются ударные волны как внутри, так и снаружи струи, а также завихрения потока в окрестности границ струи. Наиболее интенсивная ударная волна (скачок давления на ее фронте оказывается больше 10) с параболическим фронтом формируется на оси

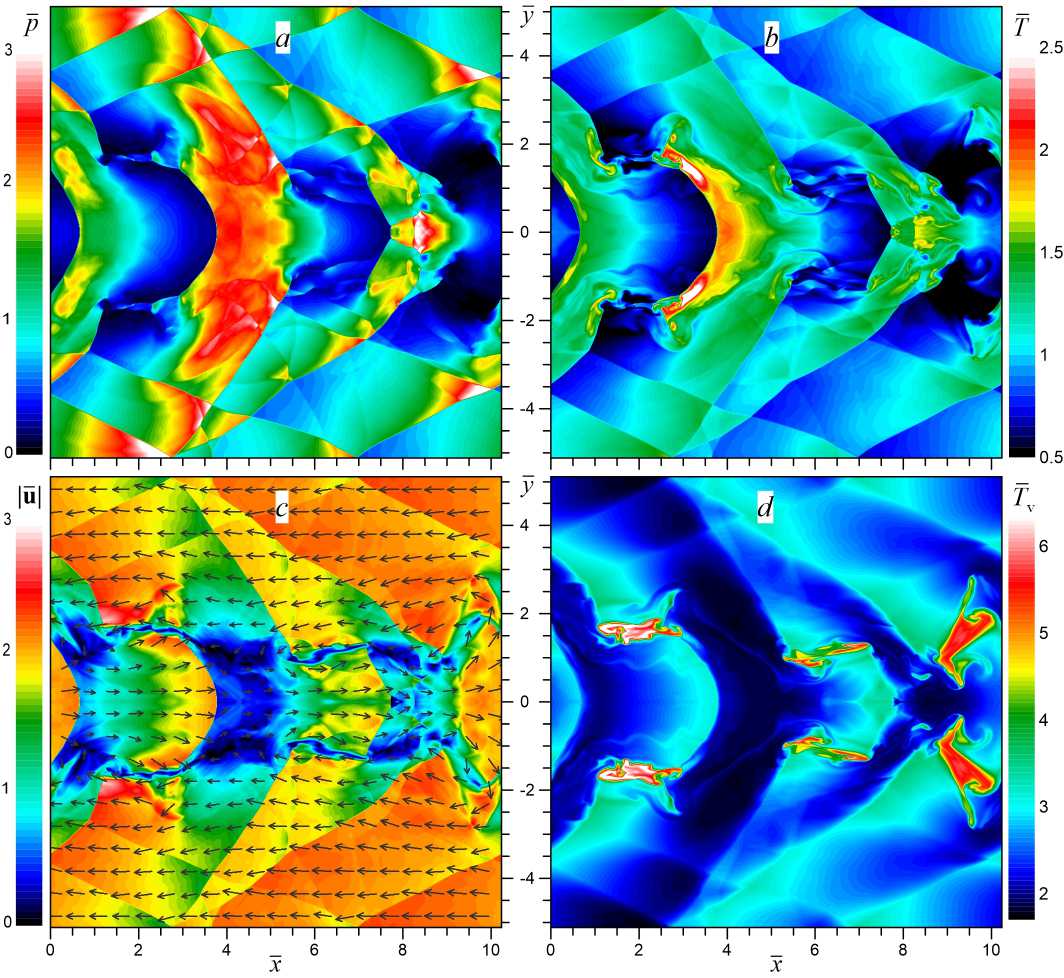
Рис. 9. Ударно-вихревая структура течения в окрестности плоской сверхзвуковой струи неравновесного газа. В момент времени t =18 показаны распределения давления (р): a — давления; b — модуля скорости; c — температуры; d — колебательной температуры струи (у = 0, х ~ 3, 5). Эта УВ движется со скоростью us ~ 0, 3 против основного потока, притормаживая струйное течение, и является аналогом так называемых дисков Маха в равновесных цилиндрических струях. Деформация плоского фронта УВ (дисков Маха) в параболический обусловлена релаксационными процессами в неравновесной среде, результатом которых является перекачка колебательной энергии в тепловую и дополнительный разогрев заударного газа [16]. Самая высокая степень неравновесности колебательно-возбужденного газа (Tv/Т) образуется в областях наиболее интенсивных вихревых течений, формирующихся в окрестности пересечения границ струи фронтами УВ, распространяющихся внутри и снаружи струйного течения (рис. 9b, d). В этих областях происходит интенсивное охлаждение газа до температур Т ~ 0, 5, а колебательная температура, наоборот, возрастает до значений Tv ~ 6, 5 (уровень колебательной неравновесности при этом достигает значений Tv/Т ~ 15), что может быть связано с развитием тепловой неустойчивости в неравновесном колебательно-возбужденном газе при наличии внешних источников накачки и теплоотвода [16].

Аналогичные результаты получаются и для изгибных мод струи, в них также формируются ударно-вихревые структуры из-за развития рассмотренных выше газодинамических неустойчивостей, но разрушение струи происходит быстрее из-за более интенсивного и крупномасштабного перемешивания встречных потоков.

Анализ результатов серии вычислительных экспериментов по исследованию нели- нейной динамики газодинамических неустойчивостей, возникающих в колебательновозбужденном газе на тангенциальных разрывах скорости течения (одного и двух в струе), показал, что с увеличением числа Маха (М0) и начального уровня неравновес-ности среды (Ту0) возрастает интенсивность и скорость образования ударно-вихревых структур. Ширина струи Н определяет пространственный масштаб наиболее неустойчивых отражательных гармоник S- и 4S-мод, длина волны которых а Н [15]. От параметра численной модели Av, определяющего амплитуду начальных возмущений, зависит время формирования нелинейных волновых структур в трансзвуковом сдвиговом потоке. Параметр численной модели h, определяющий ширину тангенциального разрыва скорости в сдвиговом потоке газа, оказывает значительное влияние только на скорость развития НКГ и нарастания отражательных гармоник струи, и не влияет на динамику акустической неустойчивости колебательно-возбужденного газа.

Заключение

Основные результаты:

• 1.    Построена двумерная газодинамическая модель неравновесной многокомпонентной среды, учитывающая следующие физические факторы: колебательно-поступательный энергообмен между молекулами (VT -релаксация), вязкость, теплопроводность, прямые и обратные химические реакции в рамках однотемпературных и двухтемпературных моделей, диффузионный перенос компонентов газовой смеси в общем потоке, нагрев газа внешним источником накачки с распределением энергии между поступательными и колебательными степенями свободы молекул, охлаждение газа внешним теплоотводом и внутренними радиационными процессами (излучением).

• 2.    Численный метод MUSCL реализован для построенной двумерной газодинамической модели неравновесной многокомпонентной среды. В этом методе использовались приближенные алгоритмы решения задачи Римана о распаде произвольного газодинамического разрыва (HLL и HLLC), обеспечивающие адекватное описание ударных волн, волн разрежения, контактных и тангенциальных разрывов. Для устранения нефизич-ных (паразитных) осцилляций численного решения применялись TVD-ограничители. Особенностью данной реализации метода MUSCL, помимо его адаптации для описания динамики неравновесных химически активных сред, является учет вязкости и теплопроводности при вычислении HLL/HLLC-потоков консервативных газодинамических величин, вместо стандартного расчета диссипативных факторов в отдельных источниковых слагаемых, которые обычно выносятся в правую часть системы газодинамических уравнений. Такой способ расчета вязких и тепловых потоков в HLL/HLLC-методе повышает как точность выполнения законов сохранения энергии и импульса, так и устойчивость численного моделирования встречных сверхзвуковых потоков с сильными ударными волнами и интенсивными завихрениями газа (ударно-вихревые течения).

• 3.    Разработан новый параллельный алгоритм метода MUSCL для численного моделирования двумерных сверхзвуковых течений неравновесного колебательно-возбужденного газа на гибридных вычислительных системах (суперкомпьютерах) с несколькими графическими процессорами (CPU – multi-GPU). Распараллеливание численного алгоритма проводилось с использованием технологий OpenMP – CUDA – GPUDirect. Анализ вычислительной эффективности разработанного параллельного CUDA-алгоритма метода MUSCL для гибридных суперкомпьютеров с GPUs показал значительное увеличение скорости расчетов по сравнению с параллельной OpenMP-версией кода для

• 4.    Проведена апробация разработанного параллельного CUDA-алгоритма метода MUSCL на двумерных задачах численного моделирования динамики трансзвуковых течений неравновесного колебательно-возбужденного газа в плоских каналах при наличии внешних источников энергетической накачки колебательных уровней молекул и теплоотвода. Решены следующие задачи исследования: 1) двумерной структуры ударноволновых импульсов (УВИ), возникающих в плоском канале из-за развития акустической неустойчивости при дозвуковом натекании колебательно-возбужденного газа на твердую стенку (в одномерной постановке эта задача рассматривалась в [18]); 2) влияния колебательной неравновесности на нелинейную динамику неустойчивости Кельвина – Гельмгольца (в линейной постановке эта задача рассматривалась в [15]); 3) влияния колебательной неравновесности на ударно-волновые структуры, формирующиеся в сверхзвуковых плоских струях на нелинейной стадии развития газодинамических неустойчивостей [15].

• 5.    Показано, что при формировании ударно-волновых импульсов (задача 1) в результате взаимодействия дозвукового потока неравновесного акустически активного газа с твердой стенкой сначала образуются первые два УВИ с плоским фронтом и постоянной интенсивностью в поперечном направлении. Затем в последующих УВИ в поперечном направлении образуются локальные максимумы в распределении газодинамических параметров течения, приводящие к изгибным деформациям фронта этих УВИ. Это связано с нарастанием амплитуды поперечных возмущений из-за развития акустической неустойчивости, что на нелинейной стадии эволюции приводит к формированию косых ударных волн, которые, многократно отражаясь от стенок канала, приводят к возникновению сложной нерегулярной (турбулентной) структуры течения как в области торможения газа перед твердой стенкой, так и в областях между фронтами УВИ, образующихся в более поздние моменты времени. Поскольку длина волны наиболее неустойчивых поперечных гармоник не изменяется с увеличением ширины канала, то в более широких каналах количество локальных максимумов в распределении параметров течения на фронте ударно-волновых импульсов возрастает.

• 6.    Получено, что колебательная неравновесность акустически активного газа усиливает газодинамические неустойчивости сдвиговых потоков с тангенциальными разрывами скорости (задачи 2 и 3). На нелинейной стадии эволюции неустойчивости Кельвина – Гельмгольца (НКГ) даже для дозвуковых режимов течения колебательная неравно-весность приводит к формированию как более интенсивных вихревых течений в окрестности тангенциального разрыва скорости, так и сложной системы пересекающихся ударных волн, которые в конечном итоге формируют единую ударно-вихревую структуру те-

• чения. Эти ударно-вихревые структуры приводят к более интенсивному перемешиванию и турбулизации встречных газовых потоков. Аналогичные ударно-вихревые структуры формируются и в сверхзвуковых струйных течениях неравновесного газа, но с более выраженной ударно-волновой составляющей, возникающей как из-за развития НКГ и неустойчивости отражательных резонансных гармоник струи, так и за счет больших значений числа Маха. Учет колебательной неравновесности, с одной стороны, приводит к формированию более интенсивных ударно-вихревых структур и более быстрому разрушению струйного течения, а с другой стороны, в таких неравновесных сверхзвуковых струях могут образовываться вихревые области с высоким уровнем колебательной неравновесности (Ту/Т ~ 15). В сверхзвуковых струях химически активных газовых смесей такие вихревые структуры с высокой степенью неравновесности могут повысить скорость протекания химических реакций, описываемых двухтемпературной моделью Парка [34].

CPU. В зависимости от количества используемых GPU (1, 2, 4) вычисления ускорились приблизительно в 200, 350 и 600 раз соответственно. Сравнение проводилось на суперкомпьютере NVIDIA DGX-1, вычислительная платформа которого состоит из 2 x CPU (2 x 20 cores) и 8 x GPU (Volta 100). При этом каждый CPU управляет работой 4 x GPU, соединенных между собой интерфейсом NVLINK, что позволяет этим 4 x GPU обмениваться между собой данными напрямую с использованием технологии GPUDirect. Для использования на этом суперкомпьютере вычислительной мощности всех 8 x GPU необходимо произвести модификацию параллельного CUDA-алгоритма с применением гибридного подхода, объединяющего технологии GPUDirect и прямого копирования данных между GPU и CPU (4 x GPUDirect + HostCopy + 4 x GPUDirect), что позволит ускорить расчеты приблизительно в 1 000 раз по сравнению с параллельной OpenMP-версией кода для CPU.

Полученные в работе результаты численного моделирования динамики трансзвуковых течений неравновесного колебательно-возбужденного газа и обнаруженные в численных моделях новые ударно-вихревые структуры могут иметь важное значение при разработке новых типов детонационных реактивных двигателей и газодинамических лазеров [12], а также экспериментальных энергетических установок для генерации мощных ударно-волновых импульсов [28; 36].