Численное моделирование генерации кратных гармоник группой плазмонных наночастиц

В работе развивается теоретическая (математическая) модель плазменных колебаний на основе функции плотности, предложенная в [1]. В качестве примера рассматриваются нелинейные колебания в металлических наночастицах при их облучении светом высокой интенсивности. Интерес механиков к данному явлению объясняется тем фактом, что более ста лет его описание традиционно базируется на методах классической механики материальных точек [2]. В настоящий момент плазмоника (междисциплинарная область, изучающая и использующая явление резонанса плазменных колебаний — плазмонный резонанс) превратилась в быстроразвивающееся направление оптоэлектроники с множеством ответвлений в различные разделы наук о материалах, такие как биофизика, коллоидная химия, механика сплошных сред и другие [2]. Перспективы ее применения связываются с областями телекоммуникаций, вычислительной техники, медицинской диагностики, фотовольтаики, спектроскопии и прочими.

Говоря об использовании моделей механики континуума для представления процессов в плазмонных структурах, следует отметить, что наибольшее распространение, по-видимому, получила нелокальная гидродинамическая модель Друде, базирующаяся на уравнении типа Навье-Стокса [3-6]. Основная область ее применения — исследование нелокальных эффектов, где уравнение употребляется в линеаризованной форме [3, 4]. В [5, 6] исследован эффект влияния конвективного слагаемого на генерацию второй гармоники в металле. В этих же работах вклады электронов, связанных с поверхностью, и электронов во внутренних оболочках атомов учтены в рамках теории нелинейной поляризации [7].

В настоящей работе расширена модель нелинейной динамики газа коллективизированных электронов (металлической плазмы), введенная ранее в [1] и более строго сформулирована аксиоматика теории. Для системы «электронный газ - ионный остов» в структуру функционала действия встроена диссипативная функция полиномиального вида. Дано определение тензора напряжений для данной системы при плазменных колебаниях. Приводится постановка начальной краевой задачи для системы интегро-дифференциальных уравнений нелинейной механики, полученных на основе принципа наименьшего действия. В рамках конечно-разностного подхода предложен численный метод и алгоритм решения этой задачи. На примере эффектов генерации кратных гармоник в электромагнитном спектре с помощью данного алгоритма проведено исследование движения электронного континуума при различных значениях параметров функции плотности и диссипативных слагаемых.

2.    Об аксиоматике теоретической модели нелинейной динамики плазмы

Принципиальный вопрос, который ставится в этой работе (и частично затрагивался в предыдущей [1]), — это вопрос о создании механики, основанной на смешанной аксиоматике. Часть положений этой механики опирается на аксиомы стандартной механики сплошной среды, другая часть — на положения квантовой механики.

Как известно [8], наиболее полным из всех возможных в квантовой механике описаний системы является описание с помощью волновой функции. Строго говоря, это осуществимо лишь для изолированных систем. На практике же квантовая система, представляющая исследовательский интерес, есть часть (подсистема) некоторой большей системы. Исследование подобных подсистем производится с помощью матрицы плотности [8]:

р ( r , r ‘ ) = | ф ( г , q ) Ф * ( r ‘ , q ) d q , ⁽¹⁾

Q где Ф( r, q) — многочастичная волновая функция; r иг’ — координаты рассматриваемой подсистемы; q — все остальные координаты большей системы; Q — конфигурационный объем. Обозначения r и q, помимо пространственных, включают в себя и спиновые переменные. Под обозначением интеграла в (1), кроме самого интегрирования, подразумевается и суммирование по спинам. Частным случаем матрицы плотности является функция плотности, служащая, во-первых, ее «диагональным» элементом р (r, r) и, во-вторых, соответствующая случаю: r е R3. Характеризация квантовых систем на основе функции плотности (точнее функционала) лежит в основе метода функционала плотности [9]. Данный метод приводит к системе нелинейных дифференциальных уравнений (уравнений Кона-Шема), близких по структуре к уравнениям Хартри-Фока. Математически р (r,r) (в дальнейших обозначениях второй аргумент опускаем, так что р (r, r) = р (r)) представляет собой функцию непрерывную и определенную в пространстве всюду. В этом смысле между квантовой механикой и классической механикой континуума наблюдается общность в «понимании» вещества: обе механики имеют дело с «континуумом плотности». Это обстоятельство позволяет отождествить количественно их функции зарядовой (массовой) плотности, а также функции плотности тока (импульса). Дискретность энергетического спектра в квантовой механике играет существенную роль для относительно небольших систем (атом, молекула), однако для объектов с тремя линейными размерами порядка нескольких десятков нанометров (состоящих из 106 г 107 атомов) энергетический спектр можно считать квазинепрерывным. В результате для таких объектов энергетические характеристики обеих механик тоже могут быть отождествлены.

Введем функцию плотности электронного континуума как р(u,uV,t), где u(r,t) е (C2(R4))3 — некоторое векторное поле, определенное всюду; uV — его градиент. Функция плотности, заданная на элементе u(r, t) превращается, таким образом, в функционал. Назовем u(r, t) функцией состояния. Будем считать, что она однозначно определяет распределение плотности вещества в пространстве, при этом функционал р(u,uV,t) будет непрерывен во всем R3. Функция состояния является некоторым обобщением функции перемещений стандартной механики континуума. Различие между ними обусловлено бесконечным характером покрытия всего пространства функцией плотности. При предположении, что континуум занимает конечный объем пространства (такое допущение было сделано в [1]) можно ввести понятия начальной и конечной конфигураций Q0 и Q1, а функцию состояния понимать в смысле отображения u(r, t): Q0 ^ Q1 (что и дает возможность говорить о ней как о функции перемещений). При таком отображении, помимо трансляции, происходит изменение формы и объема континуума. В этом случае можно говорить о его деформации и зависимости функции плотности от нее.

В качестве меры деформации в [1] выбрано тензорное поле uV = ui j eiej. Этим объясняется присутствие uV в списке аргументов функции плотности. В случае функции плотности, определенной во всем R3 и обращающейся в нуль лишь на бесконечности, возникает методологическая трудность в задании начальной и конечной конфигураций континуума, так как движение плотности не приводит теперь к изменению объема и формы «всего» R3. По этой причине постулирование зависимости р от uV имеет пока формальный характер и нуждается в поиске других мотиваций. К этому вопросу еще вернемся позднее, в разделе 3 настоящей статьи. Ввиду вышеизложенного поле u(r, t) утрачивает прямой кинематический смысл и становится внутренней характеристикой состояния механической системы. Знание u не допускает теперь проведения анализа движения «по виду» данной функции. Вследствие этого возникает потребность в формулировке необходимых мер движения.

Так, одна подходящая мера может быть получена из закона сохранения заряда. Из двух его d                   dQ                           t2

формулировок (дифференциальной-- [ р ( u , u V , t ) d ³r = — = 0, и вариационной — 5[ [ р ( u , u V , t ) d ³r dt = dt _R 3                          dt                                        t _{1 R} 3

= S { ( t 2 - t 1 ) Q } = 0 , где Q — полный заряд) следуют два дифференциальных уравнения:

др ₊ др д u ₊ др    v| д u | = о     др = др v

д t д u д t д ( u V )     ( д t J ’    д u д ( u V )

Тождественные преобразования над ними дают уравнение неразрывности:

^v- д t

д u др — дt д (uV)

Структура уравнения (3) разрешает придать выражению в скобках смысл объемной плотности тока: j = ( д u /д t ) -др/д ( u V ), которая, в свою очередь, обуславливает (с точностью до постоянного множителя) вид функции объемной плотности количества движения. Задание функции тока (импульса), а также функции плотности вида р ( u , u V , t ) дает возможность записать функцию Лагранжа системы «электронный газ - ионный остов». Применение принципа наименьшего действия приводит к уравнению движения относительно функции состояния u ( r , t ) .

3.    К формулировке принципа наименьшего действия для плазмонных систем с диссипацией

При математическом моделировании многочастичных квантовых систем их взаимодействие с внешним окружением, а также необратимые процессы в них могут быть учтены путем подбора обменных потенциалов [9]. Для классической механики более естественным приемом является внедрение в ее вариационные формулировки подходящих диссипативных функций. Именно такой подход используется автором далее. В этом контексте следует напомнить, что обобщение принципа наименьшего действия для систем с необратимыми процессами известно (см. например [10]). Строго говоря, это обобщение формализовано и помимо непосредственно диссипации пригодно для описания взаимодействия систем (или их частей) с внешними полями и материей, а также для систем с внутренними источниками энергии [10, 11].

Итак, возьмем функцию Лагранжа со структурой, приведенной в Приложении (см. также [1]) и обобщенную форму диссипативной функции D ( v ) (посредством этого предполагаем, что все диссипативные процессы определяются зависимостью от функции скорости изменения состояния: v = д^д t ). Тогда функционал действия принимает вид:

t ₂

S = lim ^^{ Л ( u , v , u V , t ) - D ( v ) } d ³ r dt , diam ^^^J J ¹

t1 Ω где Л — объемная плотность лагранжиана. Выполняя варьирование (4) с учетом стандартного условия 5u(t1) |F = 5u(12) |F = 0 (F — граница Q), получаем:

t ₂

5 S = lim diam Й^да J v t, П

—

-^-V д ( u V )

—

d дл дли dD ( v ) „ I ,₃ . --+ — l-5 u-- — -5 v ₁ ^ d ^r dt dt д v д u ) d v I

где вариации 5 u и 5 v 1 считаются пока независимыми. Потребуем, чтобы 5 v 1 = 1 c 5 u , где 1 c — единичная константа с размерностью «обратного» времени (с^-1), согласующая размерности функций в левой и правой частях данного тождества. Тогда вариация действия есть:

_         t 2 _г[Г   дл d дл дл) . dD( v ) 1 „ ,₃ .

5 S = lim HI---V--- + —I- 1 ——l-5 u d ^r dt .

^diam fi^JJ I d ( u V )      dt d V 5u J       d v

1 1 ^^\X^y

Приравнивая (5) нулю, приходим к уравнению Эйлера - Лагранжа:

дл d d дл дл _л dD ( v ) _л --V +----+ 1 c —— = 0 .

d(uV)    dt dv ди

В работе рассматриваются диссипативные функции вида D ( v ) = —— р⁺ ( r ) < V —— ( v ■ v )^0,5( p ^{+ 1)} [ ,

4 e      [ p z1 p + 1

которые порождают следующую форму диссипативных сил:

D2 = -—P+ (r) ^*p (' '

dv       4 e       17=7

где р+ (r) — зарядовая плотность ионного остова, e и m — заряд и масса электрона, n — порядок разложения, kp — коэффициенты диссипативных сил. Выбор формы представления диссипативных сил продиктован следующими соображениями. Функция общего вида D(v) может быть разложена в степенной ряд по v: D(v) = d0 + d 1 ■ v + d2 ■ ■vv + d3 ■ ■ ■ vvv +..., где di — материальные тензоры i-го ранга. В первом приближении возможно сокращение количества их компонент до некоторого минимального набора. В результате приходим к полиномиальному выражению вида (7). К слову, подобные разложения традиционно используются в нелинейной оптике для функции поляризованности P (E) (E — электрический вектор) [7]. Кроме того, выражение (7) обеспечивает связь с теорией Друде, поскольку при k1 ^ 0 и кр = 0 (для всех p > 1) из него следует обычная форма линейной диссипативной силы, используемая в теории металлов [2]. Этим, кстати, объясняется и первоначальный постулат о зависимости D от v .

Следующее требование, предъявляемое к уравнению (6), имеет аксиоматический характер. Потребуем, чтобы после дифференцирования в (6) появлялось стандартное классическое выражение для электромагнитных сил [10]: р E + j x B ( B — магнитная индукция). С этой целью проанализируем структуру производной Эйлера-Лагранжа от удельной потенциальной энергии взаимодействия континуума с электромагнитным полем (см. Приложение):

Г d d d Г д I         ■V + ( д ( u V)      dt V v d u

Ъ л      i ' др         x. d др           (      д2р ) , - j ■ А + ow } = - v-- —v ■ A ■V - ——/ ■ А + А ■ v ■ ——7  + 1 J         }     ( д ( u V)2 J      dt д ( u V)          ( д ( u V) д u J

( др | ( др |          . х др f dA , . „ , ) Г ? др _)_

+ AV„ ■ v+ vx V„ x A)+ AV„ ■ v - IрVu -V„ w , u ( d (uV) J ( d (uV) J ( u ) d (uV) (dt ( u) J (     d (uV)    J где Vu = d/du ; A (u, t) — векторный потенциал; w (u, t) — скалярный потенциал. Сформулированное требование порождает цепочку некоторых тождеств относительно функции плотности и ее производных, например:

~

I р ⁼

др д ( u V )

■ ( ~ + V u ) ,

где I — единичный тензор. Наличие тождества (8) позволяет извлечь из выражения производной Эйлера-Лагранжа стандартную форму вектор-функции напряженности электрического поля: E = - dA/дt -Vu w. С учетом того, что B =Vu x A, легко выделяется искомая форма электромагнитных сил.

Окончательный шаг к получению основного уравнения движения континуума заключается в применении процедуры разложения u(r, t) в степенной ряд. Суть процедуры состоит в том, что в произвольный момент времени t с континуумом связывается локальная система отсчета времени (в ней момент t принимается за нулевой). В этой локальной системе функция u(r, t) раскладывается в степенной ряд с последующим отбрасыванием нелинейных слагаемых, так что u(r, dt')« u(r, 0‘) + д u(J’° ) dt' = r' + v(r, 0‘) dt'

(переменные со штрихом в (9) отнесены к моменту времени в локальной системе отсчета). Все кинематические и динамические характеристики движения, содержащие функцию состояния (а также сама функция) вычисляются далее с использованием формулы (9) при условии dt'^ 0, например: др               др uV=d(r + v(r,0)dt )/дr = I . Аналогично преобразуется тождество (8): 1р =--\I + Vu) = 2

^v               "                                                                 д ( u V ) ^v ’    д ( u V )

др    р I   . д u дрp откуда следует -----= —, j =---= — и так далее.

д (uV)   2 дt д (uV)2

В итоге основное уравнение движения приобретает вид:

< — -1 (Vv + 6v V) - v + 1( V - v) v - 3 — (v - v) + 1c |р—| | У k (v - v)0,5(p ° | v [ = [дt 4(           )      2       ’     4 р       ’ c | р | l^ p ’      J А (Vp    Vp = -Vф + (E + vxB) + — —рv + v —+ Vv ,                   (10) 2 ( р       р      ) где ф (r, t) — кулоновский потенциал системы «остов-газ». Считая ионный остов неполяризующимся и немагнитным, имеем систему уравнений Максвелла в виде:

ст

Vx E = -_Ц 0     ,    Vx H = s ₀    + j + j ст ,    V- E = ^р-^р-,    V- H = 0.            (11)

д t                    д t                            s ₀

Здесь р ^ст , j ст — заданное распределение зарядов и токов в источнике электромагнитного поля; е ₀, ц ₀ — электрическая и магнитная постоянные. С помощью тождественных преобразований над (11) приходим к выражениям запаздывающих потенциалов [12]:

A ^{( r} , t ) ^- J

R3

j (r', t - c-¹ R ) + j ^ст (r', t - c-¹ R ) 3 , d r

4 n R

1 Г р (г*, t - c R ) + р ^ст (r*, t - c -¹ R )

S o R             4 n R

d ³r',

где R = | r - r' | — расстояние между точками интегрирования и наблюдения; c — скорость света. Подстановка (12) в (10) превращает это уравнение в нелинейное интегро-дифференциальное с запаздыванием относительно функций v ( r , t ) и р ( г , t ). Наличие запаздывающих объемных интегралов в уравнении (10) обеспечивает пространственно-временную нелокальность модели.

Обратимся к уравнению (6) и проанализируем структуру слагаемых с точки зрения их механического смысла. Как известно из механики классических материальных точек [13], производная дА/o v есть обобщенный импульс системы, тогда d ( дЛ/д v )/ dt — сила инерции, а производная дЛ/д u выражает объемные потенциальные силы. Таким образом, уравнение (6) представляет собой полный аналог обычного уравнения движения сплошной среды: d-V + F = pд ² u/ д t ², где &  — тензор напряжений; F — все объемные силы (потенциальные и прочие). Тогда величину дЛ/д ( u V ) в (6) следует понимать как выражение тензора напряжений с обратным знаком.

Возвращаясь к разделу 2 статьи, делаем вывод, что аксиоматическое задание зависимости функции плотности (а значит, и функции Лагранжа) от uV позволяет обеспечить соответствие уравнений предлагаемой теории уравнениям стандартной механики сплошной среды. Дополнительно появляется возможность вывести в рамках данной модели выражение тензора напряжений. Вычисляя дЛ/д(uV) и применяя (9), имеем:

дЛ р /      \?P(z а \ 7 а ) Р m f 1 z \ 7      1

а =--= — (ш + ф) I — Я v ■ A ) I - vA--- , ( v ■ v ) I - vv r.                (13)

d ( u V ) 2 ^{, M} 418 e [ 2

В классе функций Лагранжа, рассматриваемых в работе, тензор (13) определен однозначно. Из анализа его выражения следует вывод, что тензор несимметричен. Для его симметризации требуется расширение класса лагранжианов такое, чтобы в структуре производной дЛ/д ( u V ) появлялись слагаемые вида дивергенции E -V некоторого тензора E , = E j _kk e i e j e _k , антисимметричного по индексам j, k ( E,_ijk = - E ikj ) [14]. В этом случае будет выполняться тождество: ( Ё-V ) -V = 0. Возможна и другая техника симметризации (см. [14]). Последовательное построение теории напряжений в рамках предлагаемого подхода оставим до следующих публикаций.

4.    Постановка задачи нахождения состояния электронной системы

С использованием разложения (9) и уравнений (2) уравнение неразрывности (3) становится следующим:

^+ v -Vp + ^{p ( V-} v ) = 0.                                  (14)

д t              2

Объединим уравнение движения (10) и неразрывности (14) в систему, которая, таким образом, будет связанной относительно v ( r , t ) и p ( r , t ). Данную систему дополним граничным условием равенства нулю функции плотности на бесконечности: lim p ( r , t ) = 0 , а также начальными условиями: | r |^ra

v(r,0) = 0,       p(r,0) = Po(r), где p0(r) — заданная функция (форма металлической наночастицы).

Выделим класс электронных систем, которые характеризуются функцией плотности, существенно отличной от нуля лишь в ограниченной области пространства и быстро «стремящейся к нулю» за ее пределами. Поместим рассматриваемую систему внутрь некоторого параллелепипеда таких размеров, что значение функции плотности на его гранях можно считать пренебрежимо малым. Тогда систему (10), (14) будет естественно дополнить граничным условием вида:

P ( r , t )| _$ * 0, (16)

где S — суммарная поверхность граней параллелепипеда. Приближенное граничное условие (16), в плане численной реализации, представляется более предпочтительным по сравнению со строгим условием на бесконечности, поскольку допускает построение конечно-разностного аналога задачи на сетке конечных размеров. Таким образом, уравнения (10), (14) с условиями (15), (16) составляют дифференциальную формулировку задачи механики плазменных колебаний.

5.    Численная реализация

Привлекательная черта уравнений (10), (14), с точки зрения численного моделирования — их линейность относительно старших производных по времени. Это важное обстоятельство позволяет организовать шаговый по времени итерационный метод их численного решения.

Введем равномерную сетку по времени с шагом A t . Тогда первую производную по времени в (14) можно заменить первой разностью dp/d t = ( p i _{+ 1} -p i )/A t . Аналогичное выражение получим в (10) для «ускорения». Далее, при помощи равномерной прямоугольной координатной сетки с пространственным шагом A r разобьем расчетную область (в форме параллелепипеда) на элементарные ячейки. При этом каждая ячейка будет представлять собой элементарный параллелепипед. Узлами конечно - разностной сетки назначим центры тяжести элементарных параллелепипедов, тогда Vp i = ( p i , j _{+ 1} -p i , j )/ A r . Аналогичная разность будет иметь место и для градиента скорости. В результате для произвольной j -й пространственной ячейки уравнение (10) можно преобразовать к виду:

2| e                          Ai MPi        VPi11

• v.^. = v.-- ^!—^L< -Vm. + ( E. + v. x B ) +—- ■ —-v. + v. —- + V v. H-Д t +

+1                                                                              I I                                         I Ii m I                          2 I Pi          Pi

+ |(V v + 6 v V)-—- ( V ■ v )— + ^{3 Vp} ( v ■ v ) - I ¹ ^ ^-3 (V ” k (v, ■ v, )^0,5( p ^{- 1)} lv,. |д t .

• -        -       4            -v 24 pi - i> c ।pi ।        =1 pv .    .>i

  
  

Интегралы (12) вычислим по одноточечным квадратурным формулам. Узлами интегрирования назначим центры тяжести ячеек сетки. Аналогичную дискретизацию выполним и для уравнения неразрывности:

P i +i = P i ^{- (} v i ■^V P i ^{) Д} t ^{- P} i ^(V, v‘) ^Д t .

С помощью конечно-разностного аналога (17), (18) задачи (10) - (16) далее в работе исследуется динамика «металлической плазмы» на примере системы, состоящей из двух сферических наночастиц. Выбор геометрии наночастиц эквивалентен заданию начального распределения электронной плотности P ₀( r ), а также назначению ионной плотности p⁺ ( r ). Данное распределение (для одной сферической частицы) запишем в аналитической форме как

I (          ( R - 1 r - r

P 0 ^{( r )} = ^-P ^{( Г )} =P amp I ¹ -I ¹ + exP |^a---------

где R , r ₀ — условный радиус и координаты центра сферы; p _amp — среднее значение функции плотности электронного газа в частице; параметр а >  0 определяет «крутизну» спада пороговой функции ( 1 + exp ( ... )) ¹ . Для контроля качества конечно-разностной аппроксимации на каждом временном шаге алгоритма производится численная проверка закона сохранения заряда в интегральной форме:

j P ( r , t ) d ³ r = const,

V где V — объем параллелепипеда расчетной области.

6.    Моделирование нелинейной динамики в кластере наночастиц

Рассмотрим простой кластер в форме димера, состоящего из двух наночастиц серебра с условными радиусами R 1 = 30 нм и R ₂ = 22,5 нм (см. (19)). Центры частиц расположены на оси X , расстояние между центрами Д l = 56 нм. Группа частиц погружена внутрь параллелепипеда расчетной области с размерами соответственно (нм): X x Y x Z = 150 x 75 x 75 . Количество ячеек пространственной сетки зададим равным 40 x 20 x 20. С такой степенью дискретизации условию сохранения заряда в форме (20) удается удовлетворить с точностью не менее 99,9997 % на всех шагах по времени при работе алгоритма. Димер облучается нитью тока, расположенной на отрицательной полуоси Z в дальней зоне группы частиц. Вектор тока направлен по оси X . Временную форму импульса тока выберем в виде: j ст ( t ) = I ампл [ ° ( t ) -° ( t -т и )]cos(2 n f 1 1 ), где I „„, — амплитуда; т и — длительность импульса; f 1 = 450ТГц — несущая частота; g ( t ) = 0,5 + п ' arctg( в t ) — дифференцируемая ступенчатая функция («сглаженная» функция Хэвисайда), в — параметр «крутизны» ступеньки. Далее будем считать импульс узкополосным: т и f1 » 1. В окрестности димера поле источника представляет собой локально плоскую волну, вектор Пойнтинга которой направлен в положительном направлении оси Z , электрический вектор — вдоль X , магнитный — вдоль Y . Расстояние от источника до группы и ток в источнике подобраны так, что вблизи частиц амплитуда напряженности электрического поля оказывается в пределах E = 10 6 В/м, что достаточно для проявления нелинейных эффектов. К слову, данный уровень напряженности находится значительно ниже порога оптического разрушения ( > 10⁹ В/м) большинства материалов, применяемых в фотонике.

Один из принципиальных вопросов, связанных с получением решений системы (10), (14), — это вопрос о выборе свободных параметров. Наиболее значимым в контексте рассматриваемой задачи оказывается Pamp — параметр функции плотности (19). Поскольку на первом этапе работы с предложенной теорией любая априорная информация о значении рamp отсутствует (не существует простых оценок, следующих из самой теории), то для подбора значения «из первых принципов» (ab initio) приходится привлекать известные из теории металлов [2, 15] соображения об электронном строении как на уровне отдельного атома, так и на уровне кристаллической решетки. Как известно, серебро (Ag) принадлежит к первой группе элементов таблицы Менделеева и имеет электронную конфигурацию вида: 1s22s22p63s23p63d104s24p64d105s 2S1/2 [8]. Единственный электрон из незаполненной s-оболочки коллективизируется кристаллом и отвечает за металлический тип проводимости [15]. С учетом того, что кристаллическое серебро обладает решеткой ГЦК (на элементарную ячейку приходится 4 атома), получаем среднее значение плотности коллективизированных электронов как

Р amp = 4e ^ 9,39 ' IO⁹ КЛ/М 3 ,

где а = 4,086 - 10 ¹⁰ м — параметр ячейки.

Далее проанализируем то, каким образом рвходит в структуру уравнений модели. Как видно, уравнение (14) линейно по р(г, t). В результате рamp может быть вынесен из-под знака дифференциальных операторов и сокращен. В уравнение (10) этот параметр, во-первых, входит через отношение Vp/p, являющееся частью неинтегральных слагаемых, и, стало быть, также сокращается, во-вторых, появляется в подынтегральных выражениях полевых и кулоновского потенциалов и может быть извлечен из-под интеграла ввиду линейности подынтегральных выражений. В силу сказанного (10) принадлежит

5 V     (               Г              )

классу нелинейных интегро-дифференциальных уравнений вида: — = FI r, t, v, v V, р amp\Ker (r, t, v) d 3r I p u t V                  V                  )

с интегральным ядром, зависящим от параметров состояния.

Существует общая схема исследования таких уравнений на предмет существования и единственности решений, восходящая к процедуре принципа сжимающих отображений. При наличии дополнительных ограничений с помощью принципа можно показать единственность решения, но, вообще говоря, только для некоторого диапазона значений р . Более подробное исследование оставим до следующих работ. Здесь же ограничимся численным анализом системы (10), (14). Согласно результатам численного исследования оказывается, что для величины средней плотности, вычисленной по формуле (21), в диапазоне напряженностей E = 10 5 + 10 7 В/м (и, соответственно, плотностей мощности P = 10 7 + 10¹¹ Вт/м²) не удается получить решения, описывающего динамику нелинейного осциллятора. Немедленно возникает вопрос о поиске диапазона р , обеспечивающего нелинейные колебания континуума, а также о физической интерпретации его значений.

В численном эксперименте установлено, что устойчивая генерация кратных гармоник группой частиц наблюдается при величине параметра функции плотности р= 0,04 ea ³ ®- 10⁸ Кл/м³, то есть при значении на два порядка меньшем, чем предсказывает формула (21). Для объяснения этого обстоятельства выскажем следующие соображения.

Система уравнений (10), (14) применима к исследованию кристаллических решеток в условиях трансляционной симметрии. Рассмотрим бесконечный кристалл серебра. Для аппроксимации функции зарядовой плотности атомных ядер используем набор хорошо локализованных функций типа (19), для которых параметр рamp может быть найден из условия j р (r, t)d3r = 4ZAg | e |, где ZAg — атомный V -ячейки номер, Vячейки — объем ячейки трансляционной симметрии кристалла. Ячейка трансляционной симметрии представляет собой куб с параметром a = 4,086 -10-10 м, внутри которого расположены четыре атома в точках, соответствующих вершинам тетраэдра. Параметр R устанавливает для ядер атомов область их пространственной локализации (это радиус области, в которой с наибольшей вероятностью расположено ядро). Для аппроксимации электронной плотности внутренних оболочек атомов также привлекаем функции (19). Параметры этих функций подбираем из условия сильной локализации электронной плотности в окрестности ядер. Этим добиваемся частичного экранирования ядерного заряда электронным. Обе указанных функции плотности считаем статическими. Для коллективизированных электронов снова используем аппроксимацию (19), при этом параметр R назначаем исходя из условия слабой локализации (электронный газ коллективизированных электронов «размазан» по ячейке). Взаимное перекрытие функций плотности соседних ячеек кристаллической решетки учитываем при вычислении результирующей плотности электронного газа.

Параметры ρ _amp оболочковых и коллективизированных электронов изначально не известны, помимо того, что они должны совместно удовлетворять общему условию электронейтральности ячейки. На гранях ячейки трансляционной симметрии, вместо условий (15), ставим циклические граничные условия Борна - Кармана для функций скорости и плотности. Далее из системы (10), (14) удаляем электромагнитное поле и решаем ее с помощью разностной схемы (17), (18) относительно плотности коллективизированных электронов. Такой подход позволяет вычислить динамику электронной плотности в кристалле в условиях только лишь кулоновского взаимодействия, которое совместно с кинетической энергией обеспечивает наименьшее действие в электронно-ядерной системе. Далее, по распределению электронной плотности, используя (13), находим значение тензора напряжений в неэкранированной области. Отметим, что в отсутствие векторного потенциала этот тензор симметричен. Ясно, что данный тензор является мерой силового взаимодействия между электронами и ядрами, конвертированной в форму напряжений. Таким образом, компоненты тензора есть не что иное, как мера прочности кристалла, поскольку понятно, что для его разрушения необходимо приложить численно равные напряжения, но с противоположным знаком. Из сопоставления предела прочности, известного из экспериментов ( ≅ 130 ÷ 160МПа для кристаллического серебра), и уровней максимальных напряжений, вычисленных по формуле (13), получаем оценки параметров ρ _amp функций плотности как оболочковых электронов, экранирующих ядра, так и газа коллективизированных электронов в неэкранированной области. Оказывается, что для обеспечения экспериментального предела прочности необходимо, чтобы величины этих параметров отличались на шесть порядков. В этом случае для коллективизированных электронов параметр функции плотности должен составлять ρ _amp ≈ - 10⁴ Кл/м³. Причем замечено, что компоненты тензора напряжений достаточно слабо зависят от конкретных размеров области локализации ядер и размеров экранирующей электронной оболочки; требуется лишь достаточно сильное сосредоточение экранирующей плотности вокруг ядер. Так варьирование радиуса экранированной области в диапазоне R _экран = (30 ÷ 60) ⋅ 10 ^{- 12}м ≈ 0,1 a не приводит к существенному изменению значений компонент тензора.

Из результатов проведенного анализа следует, что описание континуума с помощью функции плотности (введенной в разделе 2) плохо согласуется с элементарной оценкой (21), получающейся из теории электронного строения атомов металлов первой группы. Существенную роль играет конкретный вид функции плотности системы многих частиц, при этом за формирование распределения плотности ответственен весь кристалл (как электронно-ядерная система). Оценка (21) оказалась полезной лишь в качестве отправной точки для выполнения исследований с позиций новой теории. Здесь уместно вспомнить, что параметр ρ _amp для коллективизированных электронов также может быть найден из формулы ω ² _pl = ρ _ampe ( ε ₀ m ) ^{- 1}, следующей из теории Друде [2], где ω _pl — плазменная частота, известная из экспериментов ( ω _pl ≅ 10¹⁵ ÷ 10¹⁶ Гц для серебра). Однако в этом случае ρ _amp оказывается еще большим, чем предсказывает формула (21). Сравнение полученных оценок ρ _amp = 0,04 ea ^{- 3} ≈- 10⁸Кл/м³ и ρ _amp ≈ - 10⁴ Кл/м³ позволяет сделать вывод о внесении вклада в нелинейные колебания как коллективизированными, так и оболочковыми электронами. Качественно это согласуется с существующим пониманием физики плазменных колебаний. Например, считается, что при облучении интенсивным светом вклад в них, помимо электронов проводимости, вносят также электроны из валентной зоны ( d - зоны) [2].

Далее отметим, что, помимо параметра функции плотности ρ _amp , к свободным параметрам модели относятся коэффициенты диссипативных сил k_p . Наличие диссипативных процессов в исследуемом явлении не вызывает сомнений, поскольку преобразование энергии внешнего поля в механические колебания ионных остовов, а также в конвективное тепло — экспериментально наблюдаемые эффекты [16]. На уровне межчастичного взаимодействия диссипация обусловлена различными видами квантового рассеяния. Поскольку k_p неизвестны, предположения об их величине приходится делать, отталкиваясь от имеющейся линейной теории. Уравнение (10) допускает линеаризацию при предположении об однородности полей скорости ( ∇ v = 0 ), плотности ( ∇ρ = 0 ), а также векторного ( B = ∇× A = 0 ) и кулоновского ( ∇φ = 0 ) потенциалов. При этом из (14) следует ρ ( r , t ) = const , а из (10), при условии, что k ₂ = k ₃ = k ₄ = 0 и | ρ⁺ ( r )| = | ρ ( r , t )|, — уравнение

m ( d v/ dt ) + mk ₁1 _c v = 2 e E . (22)

Стандартное уравнение Друде имеет вид: m ( d v dt ) + m ω _rel v = e E . Сравнивая его с (22), получаем:

ω rel = k 1 1 c . (23)

Множитель «2» в правой части (22) не играет роли, поскольку плотность тока в модели есть: j = ρ v I 2. В результате закон Ома, а также диэлектрическая функция электронного газа, следующие из (22), обладают неизменным «друдевским» видом (см. [2]). Формула (23) позволяет сопоставить коэффициент релаксации k ₁ со значениями ω _rel , приведенными во множестве работ по линейной теории плазменных колебаний. Значения частоты релаксации, используемые в линейных моделях (и находящие подтверждение в экспериментах), составляют: ω _rel ~ 10¹² ÷ 10¹⁴ Гц.

С помощью полной (нелинеаризованной) системы (10), (14) исследуем режим линейных колебаний в плазмонном димере. При напряженности внешнего поля E ≅ 10⁴ В/м и ρ _amp = 0,04 ea ^{- 3} ≈- 10⁸Кл/м³ получаем устойчивую динамику линейного (!) осциллятора при k ₁ ≅ 10¹⁵ (этот коэффициент безразмерен). Меньшие значения k ₁ не обеспечивают устойчивости. Таким образом, находим k ₁ на уровне плазменной частоты и выше. В случае линейной «друдевской» динамики увеличение коэффициента релаксации до уровня плазменной частоты приводило бы к сильному вязкому демпфированию колебаний, что делало бы появление плазмонного резонанса невозможным. Рассчитанное согласно построенной теории значение коэффициента диссипации порядка k ₁ ≅ 10¹⁵ всего лишь предотвращает нелинейное раскачивание системы и ее выход на закритические (нефизичные) режимы, удерживая ее в линейном режиме.

Для рассмотренного примера на рисунке 1 а приведены результаты спектрального анализа компоненты E_x электрического вектора, вычисленной в пространственной точке, находящейся в дальней зоне димера. На рисунке 1 б показаны осцилляции этой же компоненты в той же точке в зависимости от числа шагов по времени N . Число шагов по времени N принималось равным 340 . При этом временной шаг выбран так, что ∆ t = T /34 = 1/(34 f ₁) , где T — период колебаний с частотой f ₁ . Таким образом, весь процесс рассмотрен на десяти периодах колебаний основной гармоники. К полученным векторам из N значений напряженности применялось дискретное преобразование Фурье (ДПФ). В результате найдено N /2 различных коэффициентов ДПФ, представляющих веса отдельных гармоник в спектре рассеянного поля.

О 450    900   1350   1800   2250 /ТГц

Е_х , Вт/м

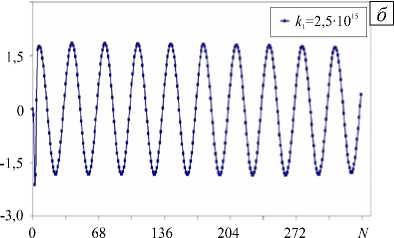
Рис. 1. Спектр напряженности электрического поля ( а ) и ее колебания во времени ( б ) в линейном случае

Примечательно, что даже в случае таких относительно малых значений напряженности не удается обойтись только линейной составляющей диссипативной силы; приходится привлекать ее слагаемые высших порядков (до четвертого включительно). В рассмотренном примере диссипативные коэффициенты имели значения: k ₂ = 10¹³ с/м; k ₃ = 10 ^{- 8} с²/м²; k ₄ = 10⁷ с³/м³.

Далее, сосредоточимся на численном анализе эффекта генерации кратных гармоник в спектре электромагнитного поля, рассеянного системой металлических наночастиц. Данное явление достаточно хорошо изучено в экспериментальных работах и подтверждено независимыми группами исследователей [17 - 20]. Генерация третьей гармоники металлическими наночастицами наблюдалась экспериментально в исследовании [17]. Этот же вид генерации продемонстрирован в [20] при возбуждении плазмонами наноотверстия сложной формы в металлическом экране. К слову, в настоящее время заметно выросла активность также в части построения теорий и математических моделей, затрагивающих различные аспекты данного вида нелинейности [5, 6].

Итак, рассмотрим примеры нелинейной динамики системы (10), (14), характеризующейся различными значениями коэффициентов диссипации. Пусть напряженность внешнего поля в окрестности частиц есть E ≅ 106 В/м. Как и в обсуждавшемся выше линейном случае, здесь не удается ограничиться выбором минимальной (линейной) конфигурации диссипативных сил. При моделировании для них использовалось полиномиальное представление четвертого порядка ( n = 4 ). Коэффициенты kp были подобраны эмпирически из условия регулярности нелинейных осцилляций (то есть они обеспечивали отсутствие роста и/или затухания амплитуды колебаний). На рисунке 2а демонстрируются результаты спектрального анализа компоненты Ex электрического вектора при двух значениях k1 (см. легенду), вычисленной в пространственной точке в дальней зоне молекулы при следующих значениях остальных коэффициентов: k2 = 1013 с/м, k3 = 10-8 с2/м2, k4 = 107 с3/м3. На рисунке 2б изображены осцилляции этой же компоненты (для трех значений k1 ). На рисунке 3а представлены спектры кинетической энергии газа в частицах, а на рисунке 3б — осцилляции кинетической энергии во времени.

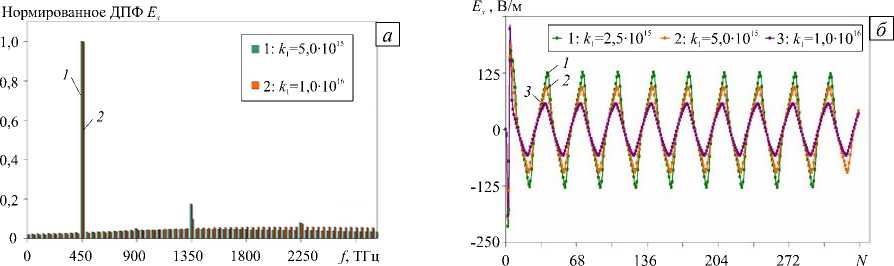
Рис. 2. Спектры напряженности электрического поля ( а ) при различных значениях k ₁ и колебания напряженности во времени ( б )

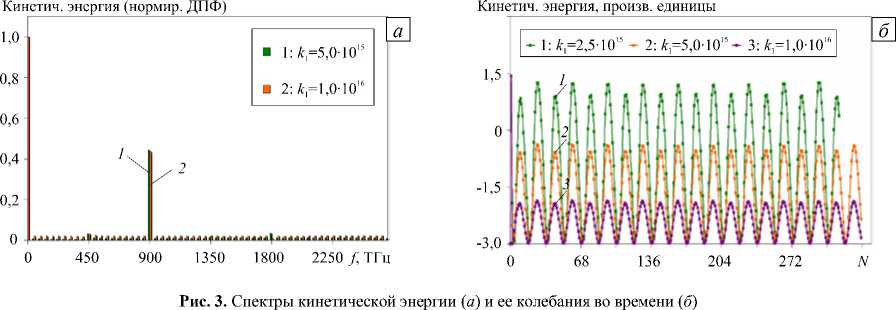
Наиболее высокий пик на рисунке 2 а соответствует вкладу фундаментальной (первой) гармоники поля на частоте f1 = 450 ТГц. Пики на частотах f₃ = 1350 ТГц и f 5 = 2250 ТГц указывают на генерацию третьей и пятой гармоник. Вследствие квадратичной зависимости кинетической энергии от скорости пиковое значение в ее спектре наблюдается на частоте: f , = 900 ТГц (Рис. 3 а ). Интересно отметить, что наиболее значимые коэффициенты в выражении диссипативной силы k ₁ , k ₂ , k ₄ соответствуют вкладам первой, второй и четвертой степеней (гармоник) скорости, коэффициент k ₃ , стоящий перед третьей степенью скорости, относительно мал, однако основным нелинейным эффектом как раз оказывается эффект третьего порядка. Таким образом, появление третьей гармоники в электромагнитном спектре полностью обусловлено структурой энергетических слагаемых функции Лагранжа, а не наличию слагаемого третьего порядка в выражении диссипативной силы.

Из полученных численных результатов также следует, что при заданных параметрах функций плотности и диссипации отклик системы оказывается в основном линейным, при этом вклады ближайших нечетных кратных гармоник (третьей и пятой) хорошо разрешаются при количественном анализе.

7.    Заключение

Как известно, принцип наименьшего действия представляет собой одно из наиболее мощных средств математической физики, используемых для получения ее основных дифференциальных уравнений. Это утверждение относится как к уравнениям механики сплошной среды, так и к уравнениям электродинамики. В этой работе с помощью принципа наименьшего действия получена система интегро-дифференциальных уравнений, описывающая нелинейные колебания газа коллективизированных электронов в металле под действием электромагнитного поля световой волны. В рамках конечноразностного подхода данные уравнения доведены до решаемой математической (компьютерной) модели.

На основе модели проведено исследование эффекта генерации кратных гармоник группой металлических наночастиц. Междисциплинарный характер исследуемого явления накладывает определенный отпечаток на область потенциального использования данных уравнений. Они, помимо электромагнитного отклика, позволяют исследовать механические характеристики движения, такие как кинетическая энергия и импульс, а также напряжения. Данное обстоятельство делает перспективным расширение сферы их применения на проблемы прочности и жесткости.