Численное моделирование ГРП в постановке Planar3D
Автор: Перепечкин И.М.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Информатика и управление
Статья в выпуске: 3 (51) т.13, 2021 года.
Бесплатный доступ
Гидроразрыв пласта является одним из основных мероприятий для интенсификиции добычи и увеличения коэффициента извлечения нефти. Для повышения предсказуемости операции ГРП и предупреждения осложнений требуется точный и быстрый инструмент. Рассматриваемый в данной статье программный комплекс, заключающий в себе быструю реализацию модели ГРП класса Planar3D, предлагается в качестве подобного инструмента. Постановка Planar3D обладает необходимой физической достоверностью для точного предсказания геометрии плоской трещины, а применение нового подхода к построению численной схемы для реализации Planar3D модели позволяет добиться высокой скорости вычислений. Построению численной схемы и численного алгоритма оценки критерия продвижения трещины посвящена данная статья.
Грп, planar3d, численное моделирование
Короткий адрес: https://sciup.org/142231494
IDR: 142231494 | УДК: 519.6 | DOI: 10.53815/20726759_2021_13_3_90
Текст научной статьи Численное моделирование ГРП в постановке Planar3D
На. настоящий момент существует иерархия математических моделей. Данные модели описывают реакцию среды, течение жидкости в трещине и другие физические процессы, происходящие при ГРП с различной степенью физической достоверности. Простые аналитические модели способны предсказывать эволюцию трещины ГРП в частных случаях, самые подробные - ветвление трехмерных трещин. Увеличение подробности модели приводит к усложнению её реализации и осмысления. Начиная с некоторого уровня подробности модели, ГРП требуют привлечения методов численного моделирования.
«Московский физико-технический институт (национальный исследовательский университет)», 2021
Всего модели, описывающие развитие трещины ГРП, можно разделить на четыре класса: аналитические, Pseudo3B, РІапагЗВ и ҒпІІЗВ.
Двумерные аналитические модели используют решение, показанное в работе [4] для плоско деформированного состояния трещины в линейно-упругой среде. В работах [5, 6] предложена основопологатощая аналитическая модель развития трещины ГРП в длину. Предположения модели следующие: трещина ограничена по высоте и подвергающейся горизонтальной плоской деформации. Предложенная модель известна как модель Христиановича-Гертсма-де Клерка (KGD). Предсказания модели KGD являются физически достоверными в случае, когда высота трещины много больше её длины, это выполняется в самом начале роста трещины от интервала перфорации.
Радиальная модель [7] описывает рост трещины ГРП в случае отсутствия контраста горных напряжений в плоскости трещины. На практике такое происходит при образовании трещины ГРП на малых глубинах, когда вертикальное составляющее тензора напряжений меньше горизонтальных составляющих. Трещина при этом развивается в горизонтальной плоскости, и горное давление, действующее на трещину, можно считать однородным. Радиальная модель также может использоваться для описания эволюции трещины в начальный момент времени при её инициализации из точечной перфорации.
Первой моделью, описывающей развитие трещины, длина которой много больше её высоты, является модель Перкинса-Керна-Нордгрена (PKN) [8, 9]. Модель описывает течение жидкости в трещине эллиптического сечения, рост трещины в длину и её раскрытие с учетом эффекта утечек. Трещина считается фиксированной по высоте.
Моделирование, позволяющее описывать вертикальных рост трещины в условиях высокой изменчивости минимальных сжимающих напряжений по пластам, может выполняться на моделях класса Pseudo3B и РІапагЗВ. Модели Pseudo3B [10] можно разделить на два типа - параметрические (Lumped-РЗВ) [11,12] и кусочно заданные (Cell-based-РЗВ) [16]. В первой трещина описывается двумя сочлененными эллипсоидами, а во второй - набором связанных ячеек, каждая их которых характеризуется раскрытием. Все модели класса Pseudo3D отличает то, что они основаны на разбиении расчетной области на элементы, в пределах которых происходит решение аналитической модели, а между собой элементы связаны уравнением баланса массы.
Модели класса Pseudo3B обычно являются численными моделями, однако существует аналитическая модель класса Pseudo3B, основанная на получении приближенного численного решения в безразмерных параметрах [14].
Отличием РІапагЗВ [15-18] модели от Pseudo3B является то, что она подразумевает решение трехмерной геомеханической задачи нахождения реакции среды на трещину и решения двумерного уравнения течения жидкости в трещине. При таком подходе отсутствует какое-либо выделенное направление, вдоль которого решаются упрощенные уравнения, как вертикальное направление в Pseudo3B модели. РІапагЗВ модели считаются очень точными, но они требовательны к вычислительным ресурсам [19].
В полностью трехмерных (ҒпІІЗВ) моделях отсутствуют ограничения на геометрию трещины [20, 21], что делает их наиболее физически достоверными. Однако высокие вычислительные затраты ограничивают использование подобных моделей в инженерной практике, ҒпІІЗВ модели используются преимущественно в научных расчетах.
Классификация моделей на аналитические, Pseudo3B, РІапагЗВ и ҒпІІЗВ главным образом определяет ограничение на геометрию трещины. Однако, кроме этого, модели можно разделить на то, с какой степенью физической достоверности они описывают различные эффекты, происходящие при гидроразрыве. С разной физической достоверностью могут быть описаны реакция среды, утечки жидкости в пласт, течение жидости в трещине и транспорт пропанта, разрушение породы и продвижение фронта трещины. Реакция среды обычно рассматривается в приближении однородной линейно упругой среды. Однако есть модели, рассматривающие эффекты реакции с учетом пластичности [22], пороупруго-сти [23] или термических эффектов [24].
С точки зрения баланса между физической достоверностью и скоростью вычислений, модель класса РІапагЗП является применимой в инженерной практике. Однако нерешенным вопросом остается численная реализация модели РІапагЗП, обладающая скоростью расчета, близкой к продвинутым вариантам Pseudo3D модели, но обладающей куда большей точностью [25]. Разработке быстрой реализации РІапагЗП модели посвещана данная статья.
2. Модель Planar 3D2.1. Положения и упрощения
В моделе РІапагЗП, рассматриваемой в данной статье, принимаются следующие положения и упрощения:
1) Считается, что гидроразрыв производится в упругой среде. Эффектами пороупруго-сти и пластической деформацией пренебрегаем. Трещина принимается за плоскую, и соответственно, она не ветвится и не изгибается. Плоскость, в которой расчет трещина выбирается такой, чтобы минимальные сжимающие напряжения в точке инициализации трещины были перпендикулярны к нормали плоскости.
2) Течение жидкости ГРП в трещине рассматривается в приближении смазочного слоя: предполагается, что раскрытие трещины много меньше чем линейные размеры трещины и не учитывается течение жидкости в направлениях, перпендикулярных плоскости стенок трещины.
3) Утечки в пласт моделируются, используя результат решения одномерной нестационарной линейной фильтрации в пористую среду.
4) Критерием разрушения породы на кончике трещины принимается силовой критерий Ирвина.
5) Транспорт пропанта моделируется в предположении теории суспензий. В описываемой модели учитывается бриджинг двух видов: бриджинг, связанный с превышением критической концентрации пропанта, и бриджинг, связанный с геометрическими размерами частиц пропанта.
2.2. Модель реакции среды
2.3. Модель течения жидкости и продвижения фронта трещины
Принимается, что процессы, происходящие в упругой среде, на порядки быстрее процессов переноса жидкости и пропанат в трещине. Это допущение позволяет решать уравнение реакции среды в стационарной постановке. В связи с тем, что трещина плоская, то, можно считать, что она делит пространство на две половины, реакцию каждой из которых можно считать отдельно. Если считать, что упругие модули одинаковы во всем пространстве, то упругую реакцию стенки трещины допустимо оценить по следующей формуле:
P(x,y) =-- z Е 2х A,'(x,y ) dx dy
8тт(1 - V 2) , //q ^Х — x )2 + (y — y )2
где P(x,y) - поле давления, Е - модуль Юнга, V - коэффициент Пуассона, П - область интегрирования, a(x,y) - поле раскрытия. Формула (1) позволят производить расчет реакции среды не только внутри трещины, но и за ее пределами. Это будет использовано при реализации критерия продвижения фронта трещины.
В уравнениях, приведенных далее, под P будет пониматься суммарное давление от реакции среды из формулы (1) и минимальных сжимающих напряжений и:
Предполагается, что длина трещины много больше её ширины, и соответственно допустимо пренебречь течением жидкости в направлении, перпендикулярном стенкам трещины. В таком случае течение жидкости в трещине ГРП приводится в приближении смазочного слоя. Ниже показана зависимость потока от градиента давления в плоской трещине для неньютоновской жидкости:
-1
q = 1 ,К / . (—vp + р ) n а П+2, 2 n +i ( 1 + 2)
где q - поток, К - коэффициент густоты потока, п - степень жидкости, д - ускорение свободного падения. Вместе с уравнением переноса формулы (1) и (3) образуют замкнутую систему уравнений, описывающую течение жидкости и реакцию среды на трещину:
д; + div(q) = £ ^source, q = ^т^ (-VP + рд)n а n +2,
р(^У) = -н^2) Л^ ^-^2^^dx dy .
Граничным условием уравнения (4) является то, что поток через границу трещины нулевой.
В качестве условия продвижения фронта трещины используется силовой критерий Ирвина [26]. Он формулируется следующим образом: трещина начинает распространяться тогда, когда коэффициент интенсивности напряжений достигает критической величины.
К т = К с .
Величину Кс ещё называют треириностойкостъю. Для определения коэффициента интенсивности напряжений К/ воспользуемся тем фактом, что асимптотически для плоской трещины напряжение за фронтом трещины выражается через коэффициент интенсивности напряжений следующей формулой [26]:
К /
V27TT ,
где г - расстояние от фронта трещины. Соответственно, для определения К / за фронтом трещины необходимо произвести аппроксимацию найденного за фронтом трещины напряжения к формуле (5).
3. Численная реализация
Явные схемы требуют значительного измельчения шага по времени. В случае решения системы уравнения (4) явным методом длительность шага по времени может составлять сотые и тысячные доли секунды. Такие результаты были получены в численном эксперименте при попытке реализовать явную схему. Из малых шагов по времени следует пропорционально большее их количество. При этом в ходе каждого шага потребуется производить взятие интеграла (1), который, как будет показано далее, имеет вычислительную сложность порядка O(N 4), г де N - характерное количество ячеек в расчетной сетке вдоль одной из осей в плоскости трещины.
Еще одним вариантом численного решения является применение неявного метода, который позволяет повысить устойчивость решения и увеличить шаг по времени. Однако специфика построения неявной схемы приводит к необходимости решения системы нелинейных уравнений методом Ньютона, что в случае построения полностью неявной схемы ведет к решению СЛАУ с не разреженной матрицей. Для уравнения (4) матрица будет полностью заполненной, так как давление в каждой точке трещины зависит от раскрытия по всей поверхности трещины. В результате, несмотря на сократившееся количество итераций, сложность самих итераций возрастет многократно.
В данной работе предлагается расщепить систему уравнений на каждой итерации по времени.
Система уравнений (4) состоит из уравнения реакции среды, уравнения для потока (3) и закона сохранения объёма.
Расчет каждого шага по времени предлагается организовать в следующей последовательности:
-
1) Производится расчет давления в трещине Р по формуле (2).
-
2) Решается система уравнений, состоящая из уравнения для потока (3) и закона сохранения объёма. Причем давление в уравнении потока учитывается как Р + dP, где dP - оценка изменения давления на следующем шаге по времени, выражение для которой будет приведено далее.
В разделении системы уравнений (4) на два выше обозначенных этапа и заключается расщепление по физическим процессам. Схематичное описание операций, производимых за один шаг по времени для явного, неявного методов и для варианта с расщеплением приведено на рис. 1, 2 и 3.
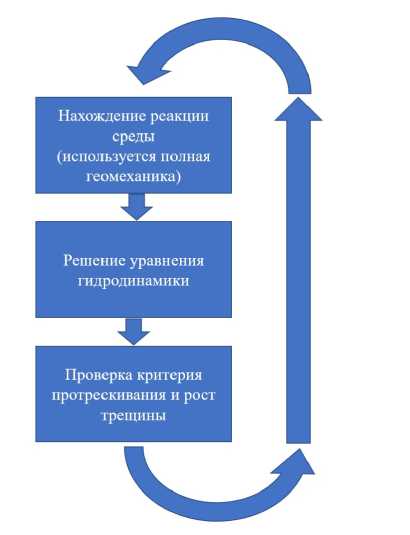
Рис. 1. Явная схема
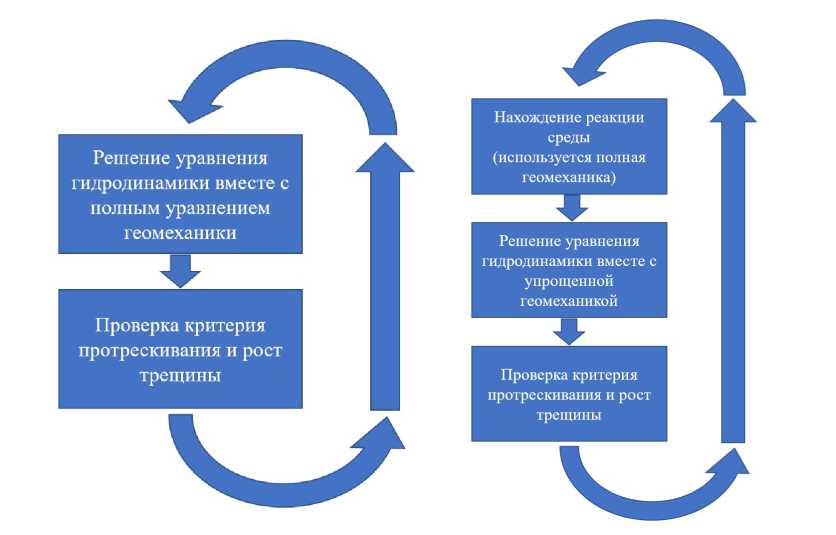
Рис. 3. Схема с расщеплением
Рис. 2. Неявная схема
3.1. Разностная схема
Для решения задачи в конечных разностях вводится двумерная регулярная сетка с квадратными ячейками. Шаг сетки по вертикальной и горизонтальной оси идентичен и обозначается как Һ. На сетке определяется дискретное поле раскрытия трещины а^. Пусть известно состояние (поле раскрытия) трещины на шаге к расчета. Обозначим раскрытие в ячейке г, j расчетной сетки как a kj. Тогда давление в каждой ячейке - результат численного интегрирования уравнения (1). Фактически полем раскрытия трещины определяется состояние трещины в каждый момент времени. При дискретизации решения уравнения (4) по времени за значение, которое необходимо найти на следующем шаге по времени, при-k+1
нимается поле раскрытия а^1 . Далее значения раскрытия и давления даны для центров ячеек, а значения потоков для граней ячеек.
-
Лk+1 ok к- - к' к- 4- + '
Чз — a ij , ^ ill/^j ^ i - 1/2,j . q ij + 1/2 ' 4j — 1 / 2
k u8ou-rce,i,j + ^leako f f,i,j,
т Һ Һ где akj - раскрытие в ячейке с индексом г,] на шаге по времени к, а^1 - раскрытие в ячейке с индексом г,] на шаге к +1, т - шаг по времени, К - шаг по пространству, VgOUTCe ■ j и ^leakoff i j площадные источники и площадные утечки в ячейке с индексом г,] на шаге к соответственно. Обозначение q^—^ j означает поток между ячейками г,] и г + 1,] на.
шаге к + 1. Соответственно qk—У j, qk j+1/2 и ^к—1/2 обозначают потоки между ячейками г,] иг — 1,], г,] + 1, г,] — 1 на шаге к + 1. Значение k k O ur Cei j отлично от нуля в ячейке инициализации трещины во время работы насоса и равно ^2, где Q - расход жидкости ГРП.
Разностная схема для уравнения баланса жидкости из уравнения (4) приведена в формуле (6). Линеаризация потока на примере дДУ j будет приведена далее. Для ^ДУ j, qkj+1/2 и k+1
i ,j- 1 / 2
q
способ линеаризации аналогичен.
3.2. Численное интегрирование реакции среды
Предлагается метод численного взятия интеграла (1). Метод основан на том, что часть интеграла предлагается взять численно, а часть - аналитически. Похожее решение предлагалось в статье [27], но в ней рассматривался другой вид интеграла. При взятии интеграла (1) основной проблемой является особая точка х,у, подынтегральное выражение в которой стремится к бесконечности. Для решения этой проблемы предлагается отделить сингулярную составляющую от Да і,j, представив интеграл в следующем виде:
^ =— 8" 2) Г Дау^ е«.„ у^
— х')2 + (y j ' —
---- dx dy , у' )2
где celli,j обозначает область ячейки с координатами г, ] на расчетной области, а Даі,j -численно рассчитанный лапласиан раскрытия в ячейке г,]. Рассмотрим отдельно подын- тегральное выражение:
^ = L >., — х' ) 2 Х+(у,' — у' ) 2 ^
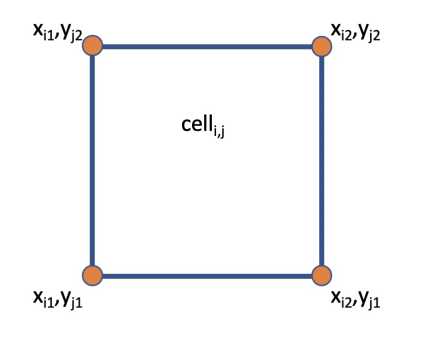
Рис. 4. Обозначение углов ячейки
Интеграл в формуле (8) не зависит от раскрытия трещины и имеет аналитическую первообразную. Значение же интеграла I,j зависит только от положения границ ячейки celli,j относительно координат х^ ,yj'\ к ,j'
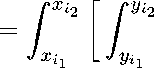
^°і' — х')2 + (yj' — у' )2
dy'j
dx =
А(х ^ ,y j ' ,X i 2,
У j 2 ) — A(x i ' ,y j ' ,x i i ,y j 2 ) —
— A(x i ', y j ', x i 2, y j i ) + A(x i ', y j ', x i i, y j i ) , (9)
где Х і1, Х і2, у 3 1 и у з 2 - координаты углов ячейки cell^ по о сям x и у, как показано на рис. 4. Функция А ( х, у, х с , ус) определяется так:
А ( х с , У с , х, у) = -(у - У с )1п( VХ 2 - 2ХсХ + у2 - 2усУ + Х2 + у2 + Х с - х)-
- ( Х с - х' )Ы( V Х2 - 2 Х с Х + у2 - 2у с у + Х2 + у2 - у с + у). (10)
Так как интеграл (9) зависит только от положения точки (хд ,у ^ ) относительно ячейки, то для случая регулярной прямоугольной сетки его можно рассчитать один раз, при Хі’ = 0 и Хі’ = 0. В дальнейшем результат вычисления интеграла при Хі’ = 0 и Хі’ = 0 можно использовать для всех ячеек расчетной сетки. Для этого интегрирование необходимо представить в виде получения дискретного двумерного поля весов W, каждый элемент г, j которой вычисляется как:
W i,j = А(0, 0 ,х і 2 ,у з 2 ) - А(0, 0,Хіі ,у з 2 ) - А(0, 0 ,х і 2 ,у з і ) + А(0, 0,Хіі ,у з і ) (И)
Дискретное поле лапласианов раскрытия, содержащую лапласианы раскрытия всей расчетной области, обозначим как Да. Дискрет ное поле Да вычисляется путем применения дискретного оператора Лапласа к дискретному полю раскрытия трещины:
Да і,з —
а і - і,3 — і + а і - і,3+і + а і+і,з - і + а і+іу+і 4К2
+
а і - 1,3 + а і+1,3 + а і,3 — 1 + а і,3 + 1 3а і3
-----------------------------------------------------Z--------------------------------------------- ---- --------Z .
2 К2 К2
Тогда двумерное поле реакции среды на трещину (перпендикулярная к трещине составляющая напряжения у поверхности трещины) вычисляется как дискретная свертка двух полей:
„ Е .
P = - - ■ W *Д 1131
Для расчета свертки в формуле (13) требуется O(N 4) операций, где N - характерный линейный размер расчетной сетки. Поэтому, данное уравнение ограниченно применимо для случая больших расчетных сеток, что важно при научных расчетах. Однако при инженерных расчетах такая асимптотика вычислительной точности расчета давления никак не оказывает решающего влияния - решение гидродинамической задачи занимает больше времени.
3.3. Линеаризация потока
Перепишем формулу (3) в новых обозначениях, где под записью (-V(P) + pg)5 понимается (-VP + pg)(| - VP + pg\)5 -1. Для краткости обозначим далее (-VP + pg) как VP, а | - VP + pg| как \VP |. В новых обозначениях формула (3) обретает вид:
8 = 1 5 ," . VP |VP15 -1а 5+2
.
2 5 +1( І + 2)
Пусть давление P^ вычислено. Тогда, по формуле ниже вычислен численный градиент давления между ячейками VP^/^ с поправкой на гравитацию:
р к, .-Рк.
V р к _ і+1,3 і,3 ,
V ^+1/2,3 = к + Р^
где ді - ускорение свободного падения вдоль индексов г расчетной сетки. Тогда аппроксимация потока из формулы (14) между двумя соседними ячейками г, j и г + 1, j вычисляется следующим образом:
. К - п
К*
qi+1/2,j = 2 П+2/ 1 + 2)
,, к I кк
VP +1/2, (|VP 1 1+1/2., )1/ " -1 ( Л1/ ) п +2 ,
где под |VPІк+і/2 j подразумевается численная оценка модуля градиента давления и гравитационного градиента между ячейками г, у иг + 1,j. Потоки между ячейками г, у иг — 1,j, г,і + 1, г, j — 1 записываются по аналогии с (15). Был найден способ аппроксимации потока на следующем шаге по времени, который позволяет свести решение уравнения (4) неявным методом лишь к одному решению СЛАУ с разреженной матрицей, без необходимости итерационного решения нелинейных уравнений.
Для оценки потока на следующем шаге воспользуемся рядом Тейлора первого порядка для потока (3):
, — , , у. у, д— . да___
q(t + dt) = q(t) + dq = q(t) + , d + dVP. да д VP
— -У
Частная производная потока по раскрытию равна д- = (1+2) да чг '
1 к - п
2 п1+2( 1 +2)
(—VP + pg) п а" +1
.
Принимается следующая численная аппроксимация частных производных у^ которая для случая потока между ячейками г, j иг + 1, j равна:
-
С-/ .
и Ә^РХ'
(di )к = (к -п da i+1/2,j гп ^2П+2( 1 + 2)
_ к I _ к
VP к Z|v р\к ) п -1 ( а i , j i+1 , j ) п+ 1
VP i+1/2,j UVP l i+1/2,j) ( 2 ) ,
dq к
к - П
OVP i+1/2, j 2 П + 2( 1 + 2)
(|VP| i+1/2,j ) П-1( а ) П + 2 .
Из формул (16), (17), (18) следует линеаризация потока У^+^ф
„ к q i+1/2 , j
к - П
21+ 2 ( 1 +2)
1 . ак . + а1
утрк . ( к . ) п 1 ( _Р2:
V Pi+1/2,j UVP И+1/2<и ( 2
к _.
' i+ 1 , j ) П+2 +
+ ( да )к +1/2’ j da^ +i/2, j
+ д Wk dVPi+i/2,j, дVPi+1/2,j
где d ak+ i/2,j
п к +1
U i+1/2,j
-
° к+1/ 2 j’ а значение dPk +1/2 j оценивается численно. Для этого
дифференциал градиента давления представляется через дифференциал давления:
dVP^ =
арк dP i+1,j
-
Һ
dP k
.
Изменение поля давления dP однозначно определяется изменением поля раскрытия трещины, это следует из формулы (1). Причем, вследствие линейности формулы (1) по раскрытию, зависимость будет аналогичной:
Е
P (ж, у, t i ) — P (ж, у, Д) = — 8Д(1—72)
ГГ Аа(ж',у‘,t 1 ) — Аа(ж',у ‘,t o ) d^ ‘ Jj Q У (ж — ж‘ )2 + (у — у’ )2 У ,
-
-
где P (ж, у, t i ) — P (ж, у, to) - изменение давления, а Аа(ж , у , И) — Аа(ж , у , to) - изменение лапласиана раскрытия. Как видно, для точной оценки dP (ж, у) требуется взятие интеграла (20) по всей области трещины. Однако для целей численной аппроксимации потока (19)
достаточно взять интеграл в некоторой области вокруг точки (ж, у). Формула для численной оценки dpk j приведена ниже:
dP k = і,з
Е 8тт(1 — v 2)
52 ^Da%",3" // i",i" Р сеііу’ ,у‘
У(ж* — ж’ )2 + (у — у’ )2
dx dy .
Формула (21) эквивалентна численному вычислению реакции упругой породы на трещину (7), за исключением того, что вместо раскрытия а берется изменение раскрытия Da между соседними шагами по времени, а суммирование предлагается проводить в области, близкой к ячейке (г, у)
3.4. Программная реализация
Программный код модели реализован на языке программирования C++, для прототипирования и отладки отдельных частей модели использовался язык программирования Python. Реализованные на C++ программные коды распараллелены с использованием ОрепМР. Программная реализация допускает возможность компиляции кода как на операционные системы Windows, так и Linux. API расчетного модуля реализовано таким образом, чтобы было возможно обращаться к нему из языка Python. Это облегчает подключение расчетного модуля к иным ПО и GUI.
4. Верификация реализованной модели4.1. Верификация критерия продвижения фронта трещины
Критерий продвижения фронта трещины, реализованный по силовому критерию Ирвина, следует проверять вместе со всеми остальными уравнениями на таком кейсе, для которого точно известно аналитическое решение задачи гидроразрыва. Классические аналитические модели для этого не подходят, так как в них никак не учитывается влияние трещиностойкости. Однако была найдена постановка задачи, для которой можно найти простое аналитическое решение, учитывающее влияние трещиностойкости.
Постановка задачи следующая: пусть в однородный упругий пласт с нулевым коэффициентом утечек и с ненулевой трещиностойкостью происходит закачка текучей жидкости. В таком случае трещина окажется круглой. Какое-то время после окончания закачки она будет растекаться. Это будет происходить до тех пор, пока коэффициент интенсивности напряжений за фронтом трещины больше трещиностойкости. Когда коэффициент интенсивности напряжений станет равен трещиностойкости породы, рост трещины прекратится на определенном радиусе Рк, который можно оценить аналитически. При этом закачка жидкости должна происходить с достаточно высоким расходом, чтобы радиус трещины к моменту окончания закачки был хотя в несколько раз меньше Рк-
Опишем предложенную постановку задачи формально. Пусть в породу с модулем Юнга Е, коэффициентом Пуассона v и трещиностойкостью K j max была с высоким расходом закачена жидкость объема V. К тому моменту, как трещина в процессе растекания достигнет своего передельного радиуса, будем считать трещину эллиптической. Давление в такой трещине будет равно [28]:
р к =
а к ^Е
8(1 — v2 )Р к .
Раскрытие трещины а к вычисляется исходя из формулы для объема эллипсоида:
3V ак = 2^Р2:. к
Интенсивность напряжений за фронтом эллиптической трещины радиуса Рк, давление в которой равно Рк, вычисляется по формуле [29]:
Ki = 2рк R^ .
Воспользовавшись формулами (22), (23) и (25), нетрудно показать, что радиус трещины на момент окончания растекания, когда K i = K i max, будет равен
R k = (3 Л ')
\ 8 K imax (1 - v2) VttV
Т а б л и ц а 1
Основные параметры среды и закачки
|
Название параметра |
Обозначение |
Значение |
|
Модуль Юнга среды Коэффициент Пуассона Объем закачки Трещиностойкость |
Е v К K i max |
10 ГПа 0 20 м3 5е5, 1еб и 2.5еб ПаДД |
Формула (25) позволяет проводить верификацию работы критерия продвижения фронта трещины путем сравнения R k с результатом численного расчета.
Для сравнения использовались параметры, приведенные в табл. 1.
В численных расчетах закачка 20 м3 жидкости производилась за 500 секунд. На установление состояния трещины после окончания закачки отводилось 160 000 секунд. Вязкость закачиваемой жидкости равна 1 сп. Размер расчетных ячеек - 5 метров.
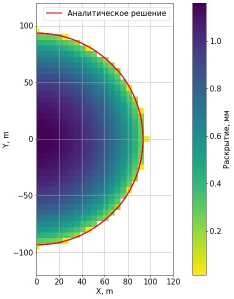
Рис. 5. Kjmax = 0.5 ГПафД
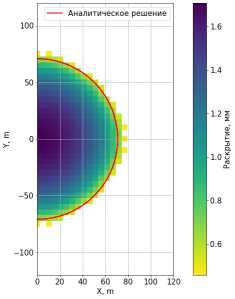
Рис. G. Kimax = 1 ГПафД
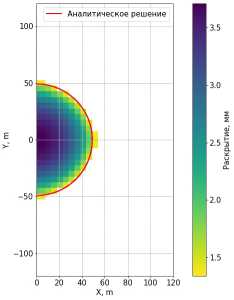
Рис. 7. Ki max = 2.5 ГПафД
На рис. 5, б и 7 приведено сравнение аналитического и численного решений. Как видно, наблюдается совпадение численного и аналитического радиуса трещины с точностью до размера ячейки, что можно интерпретировать как то, что удалось реализовать простой, но при этом достаточно точный критерий продвижения фронта трещины.
4.2. Сравнение с ILSA
Для сравнения с ILSA была выбрана статья за авторством Е. V. Dontsov и А. Р. Peirce [27], в которой есть несколько кейсов, описывающих работу их Planar3D модели с ILSA критерием продвижения фронта трещины. Соответственно, сравнение результатов расчета реализованной в данной работе модели с кейсами из данной статьи позволит не только оценить адекватность реализации модели течения в трещине и расчета реакции среды, но и оценить обоснованность выбранного критерия продвижения фронта трещины.
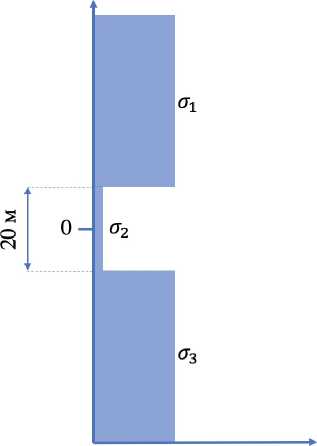
Будут рассмотрены кейсы в трехслойной среде, схема которой с обозначениями приведена на рис. 8. Упругие модули среды и параметры закачки приведены в табл. 2.
Т а б л и ц а 2
Параметры среды и закачки
|
Название параметра |
Обозначение |
Значение |
|
Модуль Юнга среды |
Е |
9.5 ГПа |
|
Коэффициент Пуассона |
7 |
0.2 |
|
Вязкость жидкости ГРП |
^ |
0.1 Па с |
|
Расход жидкости |
9 |
0.01 З |
|
Коэффициент утечек |
CL |
0.2605, 0.825 и 2.605 -^е-5 VC |
|
Время закачки жидкости |
Т |
3600 с |
Сжимающие напряжения, a
Рис. 8. Трехслойная среда для сравнения с ILSA
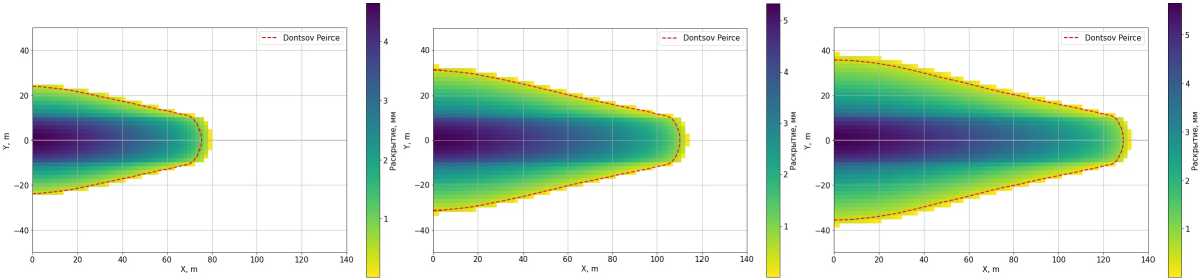
Рис. 9. CL = 2.605е-5 ^ Рис. 10. CL = 0.825е-5 ^ Рис. 11. CL = 0.26С)5е-5 Д=
^ Ус ^ ^ Vе
Для симметричного случая напряжения приняты такими: < i = 7 3 = 7.75 МПа, <72 = 7 МПа. Результаты расчетов на описанной в этой работе модели Planar3D при различных утечках на момент времени 3600 секунд от начала закачки приведены на рис. 9, 10 и 11. На рисунках показано поле раскрытия с размерностью в метрах. Геометрия трещин с точностью до размера одной-двух ячеек, составляющего 1.8 м, совпадает с результатами, приведенными в статье [27].
Для асимметричного случая с высоким контрастом между верхними слоями напряжения равны: < 1 = 7.25 МПа, 72 = 7 МПа, 7 3 = 6.5 МПа. Результаты расчетов для этого случая приведены на на рис. 12, 13 и 14. Геометрия совпадает с той, что приведена на соответствующих рисунках в статье [27] с точностью до размера ячейки.
Совпадение геометрий трещины при моделировании на предлагаемой в этой работе модели Planar3D с результатами ILSA Planar3D позволяет говорить о том, что в предложен- ной модели корректно реализована гидродинамическая и геомеханическая часть. Также подтверждается корректность выбранного критерия продвижения трещины.
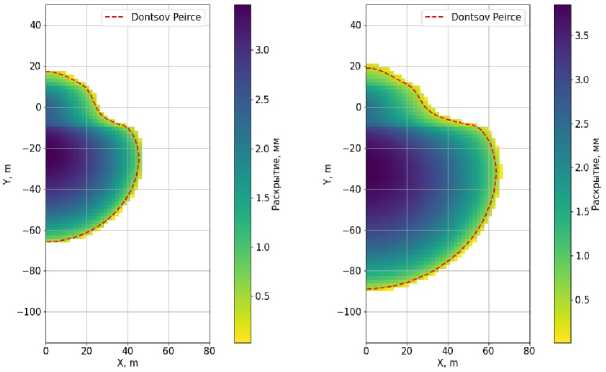
Рис. 12. CL = 2.G05C-5 ^
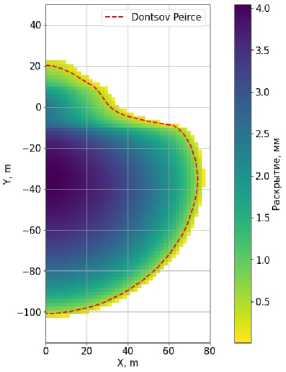
Рис. 14. CL = 0.2G05c-5 ^ Vе
Рис. 13. CL = 0.825С-5 ^ Vе
5. Программная реализация
Программный код модели реализован на языке программирования C++ для прототипирования и отладки отдельных частей модели использовался язык программирования Python. Реализованные на C++ программные коды распараллелены с использованием ОрепМР. Программная реализация допускает возможность компиляции кода как на операционные системы Windows, так и Linux. API расчетного модуля реализовано таким образом, чтобы было возможно обращаться к нему из языка Python. Это облегчает подключение расчетного модуля к иным ПО и GUI. В качестве бенчмарка скорости работы программной реализации и демонстрации эффективности численного алгоритма был выбран кейс, показанный на рис. 14. Кейс представляет собой закачку 36 м3 жидкости при размере расчетной ячейки 1.8 метров. Время расчёта этого кейса на ПК с процессором Intel Core І5 7600k составляет 62 секунды в однопоточном режиме и 37 секунд при распараллеливании расчета на 4 потока.
6. Дальнейшее развитие модели
Модель, описанная в уравнении (4), может быть расширена для расчета транспорта пропанта и течения нескольких жидкостей в трещине.
6.1. Транспорт пропанта
Моделирование транспорта пропанта производится в предположениях теории суспензий.
I
^^ + dw(q p ) = £ ^ source prop , ^ " + div(q j ) = ^ ^ source fluid *
При этом пропант моделируется как отдельная фаза, и для него записывается отдельное уравнение баланса масс, как показано в уравнении (26), где C - объемная концентрация пропанта, qp - поток пропанта, q j - поток жидкости.
q s = q p + q j =
К
n
2 П + 1( 1 +2)
(-VF + pg) n a ”+2(1
C
-
C max
)
т
n
*
В формуле (27) C max - максимальная объемная концентрация пропанта, m принимается равной 1,89. Потоки qp и q j выражаются через средний поток смеси, выражение для которой приведено в формуле (27). Формула (27) аналогична формуле для потока жидкости с тем различием, что коэффициент густоты потока Ks для смеси пропант-жидкость предполагается равным:
/ С х 5-
K s = К (1 - —) 2 .
Для моделирования эффектов оседания пропанта вводится понятие отрыва скорости пропанта от жидкости:
Vp = Vs + (1 - с)Д V, где Vp = qp/сц a Vs = qs(а. Для скорости отрыва пропанта предлагается следующее выра жение:
ДV =
-
gradP + p p д ^ (1
C
18ді
-
C max
^ m
где d - диаметр частицы пропанта.
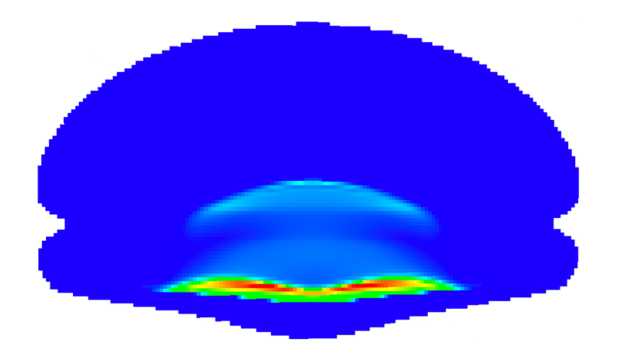
Рис. 15. Моделирование оседания пропанта в трещине
На рис. 15 качественно приведено распределение пропанта для кейса, похожего на тот, что был приведен в статье за авторством Cohen Charles-Edouard et al. [25].
6.2. Течение нескольких жидкостей
В процессе проведения ГРП в трещину закачивается несколько типов жидкостей. Обычно это линейный гель, которым заполнена насосно-компрессорная труба (НКТ), и сшитый гель, которым производится накачка подушки и транспорт пропанта в трещину.
Течение нескольких жидкостей описывается системой уравнений баланса массы, состоящей из уравнений типа (29) для каждой жидкости.
ЭаС^
dt
+ divq^ = V f^
где q ji - по ток г-й жидкости, a C fi - её объемная концентрация. Основной проблемой при моделировании течения нескольких жидкостей в трещине ГРП является вопрос оценки потока смеси жидкости q j и потока отдельных жидкостей. Предложим следующую модель, построенную на следующих предположениях:
-
1) Жидкости не испытывают взаимного трения.
-
2) Каждая из жидкостей занимает все пространство между стенками трещины.
Тогда для каждой отдельной жидкости остается применимым приближение смазочного слоя и соответственно потока г-й жидкости выражается так:
-
Кгн qf. = сг -------
2”* (^ + 2)
1_ __-2
(-VP + pg)nf< и"
При этом поток смеси - сумма потов всех жидкостей:
N qf = У 9fi .
Приведенная модель течения нескольких жидкостей позволяет с высокой точностью моделировать случай поршневого вытеснения, когда по ходу закачки вязкость увеличивается. При нестабильном режиме вытеснения, когда текучая жидкость вытесняет вязкую, вязкие пальцы не разрешаются, однако возникает эффект фильтрации текущей жидкости через вязкую - что качественно верно.
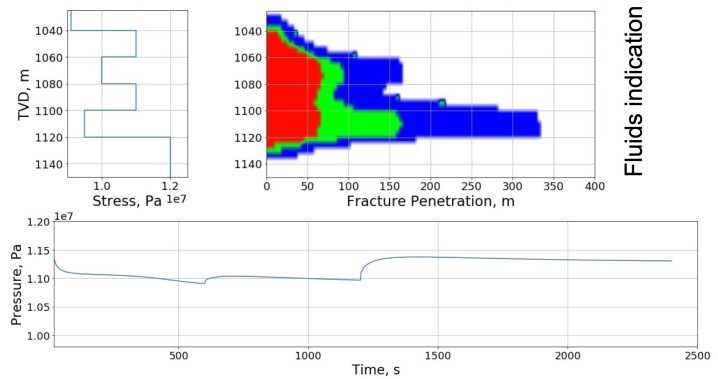
Рис. 16. Моделирование течения нескольких жидкостей в трещине
На рис. 16 показан пример расчета с течением нескольких жидкостей, закачиваемых в следующем порядке (в скобках указаны параметры степенной жидкости): (К = 0.05, п = 1.0), (К = 0.5, п = 0.9), (К = 5, п = 0.55). Так как вязкость жидкостей возрастает, то наблюдается поршневое вытеснение и возрастание забойного давления с каждой новой стадией.
7. Заключение
Разработан новый подход к численному моделированию ГРП в постановке Planar3D, заключающийся в расщеплении по физическим процессам. Реализованы вычислительные алгоритмы, решающие уравнения Planar3D согласно разработанному подходу путем решения уравнения явно-неявным методом. Разработан численный алгоритм, реализующий проверку критерия продвижения трещины по силовому критерию Ирвина. Верификация подтверждает корректность программной реализации и численной схемы.
Список литературы Численное моделирование ГРП в постановке Planar3D
- Шевченко Д.В., Шевченко В.П. Выбор и оптимизация структуры построения автономных сейсмических средств обнаружения рубежного типа // Материалы VIII всероссийской научно-технической конференции «Современные охранные технологии и средства обеспечения комплексной безопасности объектов». 2010. С. 128-133.
- Diallo M.S., Kulesh М., Holschneider М., Sherbaum F., Adler F. Characterization of polarization attributes of seismic waves using continuous wavelet transforms // Geophysics. 2006. V. 71, N 3. P. 67-77.
- Лайонс P. Цифровая обработка сигналов. Москва : Бином, 2006. С. 361-369.
- Sneddon I.N. The distribution of stress in the neighbourhood of a crack in an elastic solid // Proceedings of the Royal Society of London A: Mathematical Physical and Engineering Sciences. 1946. V. 187, N 1009. P. 229-260.
- Khristianovich S.A., Zheltov Y.P. Formation of vertical fractures by means of highly viscous liquid // Proceedings of Fourth World Pet. Congress, Rome. 1955. V. 2, P. 579-586.
- Geertsma J., Klerk F.A. Rapid method of predicting width and extent of hydraulic induced fractures // J. Pet Tech. 1969. V. 12. P. 1571-1581.
- Zazovskii A.F. Growth of coin-shaped crack produced by hydraulic fracture in an impermeable rock 11 Mech. Solids. 1979. V. 2, N 14. P. 104-111.
- Perkins Т.К., Kern L.R. Widths of Hydraulic Fractures //J. Pet. Technol. 1961. V. 13. P. 937-949.
- Nordgren R.P. Propagation of a vertical hydraulic fracture // SPE 3009-PA. 1972.
- Mack M.G., Warpinski N.R. Mechanics of hydraulic fracturing, Reservoir stimulation, 3rd ed. Chichester : Wiley, 2000. P. 856.
- Cleary M.P. Analysis of mechanisms and procedures for producing favourable shapes of hydraulic fractures 11 SPE 9260-MS. 1980.
- Meyer B.R. Design formulae for 2-D and 3-D vertical hydraulic fractures: model comparison and parametric studies // SPE 15240-MS. 1986.
- Smith M.B., Klein H.A. Practical Applications of Coupling Fully Numerical 2-D Transport Calculation With a PC-Based Fracture Geometry Simulator // SPE 30505. 1995.
- Шель E.B., Падерин Г.В. Модель для экспресс-оценок дизайна ГРП с использованием приближенного аналитического решения / / PRO НЕФТЬ. Профессионально о нефти. 2017. № 4(6). С. 40-43.
- Barree R.D. A practical numerical simulator for three-dimensional fracture propagation in heterogeneous media 11 SPE 1227 3-MS. 1983.
- Smith M.B., Klein H.A. Practical Applications of Coupling Fully Numerical 2-D Transport Calculation With a PC-Based Fracture Geometry Simulator // SPE 30505. 1995.
- Adachi J., Siebrits E., Peirce A., Desroches J. Computer simulation of hydraulic fractures // International Journal of Rock Mechanics k, Mining Sciences. 2007. P. 739-757.
- Аксаков А.В., Борщук О. С., Желтова И. С., Дедурин А.В., Калуджер 3., Пестри-ков А.В., Торопов К.В. Корпоративный симулятор гидроразрыва пласта: от математической модели к программной реализации // Нефтяное хозяйство. 2016. № 11. С. 35-40.
- Nolte K.G., Economides M.J. Reservoir Stimulation Chichester, NY : John Wiley k, Sons, 2000.
- Clifton R.J., Abou-Sayed A.S. On the computation of the three-dimensional geometry of hydraulic fractures // SPE 7943-MS. 1979.
- Carter B.J., Desroches J., Ingraffea A.R., Wawrzynek P.A. Simulating fully 3D hydraulic fracturing // Modeling in geomechanics. 2000. V. 200. P. 525-557.
- Zeng Q., Yao J., Shao, J. Effect of plastic deformation on hydraulic fracturing with extended element method // Acta Geotech. 2019. N 14. P. 2083-2101.
- Baykin A.N., Golovin S. V. Modelling of hydraulic fracture propagation in inhomogeneous poroelastic medium 11 J. Phvs.: Conf. Ser. 2016. V. 722, N 012003.
- Clifton, R.J., Wang J.J. Multiple Fluids, Proppant Transport, and Thermal Effects in Three-Dimensional Simulation of Hydraulic Fracturing // 63rd Annual Technical Conference and Exhibition in Houston, TX, 1988.
- Cohen C.-E., Kresse O., Weng X. Stacked Height Model to Improve Fracture Height Growth Prediction, and Simulate Interactions With Multi-Layer DFNs and Ledges at Weak Zone Interfaces // SPE-184876-MS. 2017.
- Матвиенко Ю.Г. Модели и критерии механики разрушения. Москва : Физматлит, 2006. С. 328.
- Dontsov Е. V., Peirce А.P. A multiscale Implicit Level Set Algorithm (ILSA) to model hydraulic fracture propagation incorporating combined viscous, toughness, and leak-off asvmptotics // Computer Methods in Applied Mechanics and Engineering. 2017. V. 313. P." 53-84.
- Martin P.A. On wrinkled penny-shaped cracks // Journal of the Mechanics and Physics of Solids. 2001. V. 49. P. 1481-1495.
- Мураками Ю. Справочник по коэффициентам интенсивности напряжений: В 2-х томах. Т. 2. Москва : Мир, 1990. 1016 с.


