Численное моделирование инвариантности оценки знания относительно трудности тестовых заданий в рамках модели Г.Раша

В связи с переходом наших Вузов в балльно-рейтинговую систему стало нормой плановое проведение контроля знания студентов по каждому модулю учебной дисциплины. Для успешного выполнения систематической оценки знания привлекается тематическое тестирование в дополнение к традиционным видам контроля знания [1-4].

Но здесь сталкиваются со следующей проблемой: не всякий тестовый набор заданий в состоянии обеспечить достоверную оценку знания. Известно [5], что тесты с высоким уровнем трудности приводят к заниженным оценкам испытуемых, и наоборот, легкие тесты завышают результаты тестирования. Только профессиональное проведение тестирования и корректное применение математико-статистических методов современной теории тестов для анализа данных тестирования позволяют получить достоверные оценки знания, не зависящие от трудности тестовых заданий. Продемонстрируем процедуру математической обработки результатов теста, необходи- мой для объективной оценки знания, на примере упрощенного численного моделирования процесса тестирования.

С овременная теория тестов и модель Раша

Под названием современная теория тестов понимают известную за рубежом теорию Item Response Theory (IRT), основу которой составляет модель Раша [6]. Модель Раша исходит из положения, что вероятность правильного ответа i-того испытуемого на j-тое тестовое задание определяется разностью латентных (скрытых) параметров θi - βj - уровней обученности испытуемого и трудности задания и описывается функцией успеха ij

11 + exp(-1.73(0 - в ))

Георг Раш предположил , что эта математическая модель устанавливает взаимосвязь между эмпирическими результатами тестирования и значениями латентных параметров θ_i и β j , при этом уровень обученности испытуемого θ_i и уровень трудности задания β j размещены на одной шкале и измеряются в одних и тех же единицах – логитах.

Существует несколько методов определения латентных параметров  θi и βj непосредственно из эмпирических данных тестирования, представленных дихотомической матрицей Xij , когда за верный ответ ставится 1, а за неверный ответ - 0.

Для вычисления этих величин θ i и β j воспользуемся методом параметризации, процедуру которого изложим, следуя М. Челышковой [5 ].

Индивидуальный балл i –того испытуемого определяется из выражения

m

X^ Xj

j откуда следуют доли верных

X

и неверных

qi = 1- Pi

ответов ис-

пытуемых, где m - количество заданий в тесте. На основе этих величин производится предварительная оценка обученности в логитах

00 = In pi- qi                                         (3)

Количество правильных ответов на j- тое задание вычисляется по формуле

n j  ^vj                        (4)

i

Rj и подсчитываются доли правильных

pj    ^ и неправильных ответов qj=1-pj на это задание, где n - число испытуемых в группе.

Предварительная оценка трудности задания производится в логитах

p j

На следующем этапе начальные значения логитов обученности и трудности заданий переводятся в единую интервальную шкалу стандартных оценок. Стандартизация достигается с помощью ряда специальных преобразований [7], для осуществления которых вычисляются:

• •    среднее значение 6 для множества 6 0 (i = 1,2,...,n) подсчитывают по формуле

N

_ X60

⁶ = -—,                      (6)

где 6 0 — предварительные значения уровня обученности i -го испытуемого;

• •    среднее значение в для множества P 0 (j = 1,2,...,m) равно

  n

  
  
  

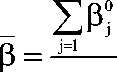
  m

  
  
  
  

  где в 0 — предварительные значения логитов трудности заданий; • дисперсия по множеству значений 6 0 (i = 1,2,...,n)

  
  

  n

  X ill >  - n( 6 )²
  
  V = —------- n -1

  
  
  
  

  • •    дисперсия по множеству P 0 (j = 1,2,...,m)

  m

  X ( в0 ) ² - m( P ) ²

  U = ^j---------- ,

  m — 1

  • •    поправочные коэффициенты

  
  
  
  

  _x     1 + U /2,89
  
  - v 1 - UV /8,35,

  
  
  
  

  Y =

  
  

  1 + V/2,89

  
  

  v 1 - uv/8,35.

  
  
  
  

Конечные оценки параметров в единой интервальной шкале находятся по формулам

6k. = в + Хв

i                          i ,

Bk, = в + YB0 j                      j,

Последние формулы (12) и (13) современной теории тестов обеспечивают объективность параметров испытуемых и заданий и независимость друг от друга оценок обученности и трудности задания. Но на практике, как отмечает В.Аванесов [8] , результаты не всякого тестирования согласуются с моделью Раша. Несоответствие эмпирических данных модели Раша может означать, что были нарушения в процедуре тестирования или при анализе эмпирических данных. Некоторые авторы [9, 10] пытаются улучшить теорию для того, чтобы она точнее описывала экспериментальные данные, или ведут поиски других моделей, более адекватных полученным результатам.

Здесь есть принципиально важный момент. В теории Г.Раша никогда не ставилась задача адекватного описания данных. Напротив, утверждается противоположное – не модель должна соответствовать эмпирическим данным, а данные должны соответствовать модели. В теории педагогических измерений применяется иной подход, нежели в естественных науках. Если в физике законы природы не зависят от исследователя, то тесты в немалой степени зависят от его воли. Поэтому физики стараются развить модель для лучшего согласия с экспериментом, а тестирование необходимо проводить, строго выполняя требования теории. В соответствии с этим педагогический тест образуют только те задания, которые отвечают данной модели измерения. Все остальные в тест не включаются.

Численное моделирование процесса тестирования

Проведем моделирование процесса тестирования в рамках модели Раша с целью изучения вопроса, как влияет трудность тестовых заданий на оценку знания испытуемых. Вначале установим масштаб изменения латентных параметров. Отечественная пятибалльная шкала позволяет оценивать знания учащихся с точностью не более 20%, а возможности тестовой технологии определения уровня обученности значительно выше. Но на практике достаточно ограничиться такой точностью вычисления вероятности правильного ответа по формуле успеха (1), которая обеспечивается интервалом изменения латентных параметров θ i и β j в пределах от -3 и до +3 единиц логитов, а погрешность измерения этих параметров допустим, равной Δθ~Δβ~0,3 логит [11].

Численные расчеты удобно проводить в среде MathCad, которая имеет широкие возможности стандартных статистических обработок числовых массивов и графических построений. Выберем в качестве испытуемых одну академическую группу из n=25 студентов с нормальным распределением θ - уровней обученности. С помощью функции θ = rnorm (25,0,1) образуем массив θ обученности из случайных чисел, распределенных по стандартному нормальному закону с численными характеристиками среднего значения θs=0 и стандартного отклонения Sxθ=1, а затем проведем процедуру упорядочивания этого массива по возрастанию значения θ уровня обученности. При этих характеристиках нормального распределения значения θ заключены в интервале (- 3,+3) и совпадают с принятым масштабом изменения уровня обученности.

Теперь установим масштабы изменения трудности тестовых заданий. Будем считать, что имеется банк тестовых заданий калиброванной трудности. Из опыта проведения тестирования [8] выявлено, что уровень трудности теста должен соответствовать уровню обученности испытуемых. Нет смысла задавать слабо подготовленным трудные задания, с которыми они заведомо не справятся, и наоборот, легкими вопросами не установить уровень знания. Поэтому выберем трудность теста, соответствующую уровню обученности группы. Зададим число заданий m=30 с интервалом изменения трудности в тех же пределах, что и интервал обученности группы, полагая равномерное распределение их. Среднее значение этого массива заданий равно βs =0, т.е. выдержано еще одно требование - сбалансировано число трудных и легких заданий в тесте.

Наконец, проведем моделирование процесса тестирования указанной группы испытуемых в рамках модели Раша. Согласно модели Г. Раша в качестве результатов тестирования оперируют не дихотомическими константами 0 и 1, а суммарной вероятностью ответа i – того испытуемого на задания теста, определяемой по формуле успеха (1):

m

Xi =

∑ P ij

j

А суммарную вероятность правильных ответов на j-тое задание всей группой испытуемых определим по формуле

n

R j =∑ P ij i ^,

Дальнейшие расчеты латентных параметров проведем по выше изложенной процедуре с переопределенными величинами (14) и (15). При предположении о наличии банка заданий калиброванной трудности задача сводится к нахождению только параметра обученности и на анализ следующих его значений:

• •    предварительные значения θ0, определенные в логитах по формуле (3) и

• •    конечные значения θk, вычисленные в интервальной шкале по формуле (12). Завершается анализ установлением требований к процедуре тестирования, которые обеспечивают согласие расчетных значений обученности θk с исходным θ по критерию хи-квадрат

  θ k i - θ i 2

  Δ θ

  
  
  
  

n χ2(θk -θ) = 1∑ ( ni

Имея тестовые задания с равномерным распределением β трудности, проведем моделирование процесса тестирования в группе испытуемых с нормальным распределением θ обученности и определим параметры θ0 и θk, значения которых представлены на рис.1, где сравниваются с исходной θ обученностью.

Кривые этих распределений пересекаются при β ~ θ ~ 0 так, что до пересечения трудность задания оказалась ниже обученности испытуемых, а после пересечения выше ее. Что приводит к тому, что предварительные значения обученности θ0 испытуемых оказываются завышенными при низкой трудности задания и заниженными при высокой трудности заданий. Вследствие равенства средних значений трудности βs=0 и обученности θs=0 их различия незначительны, в пределах допущенной погрешности, что подтверждается вычислением критерия χ2 (θ0-θ) = 0,78.

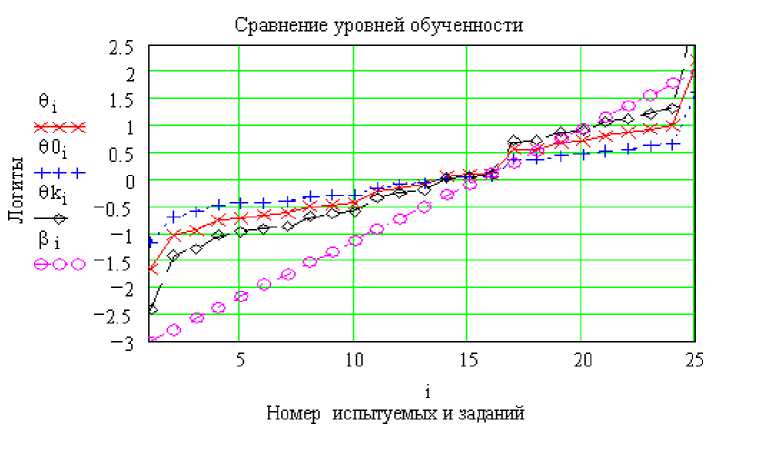
Рис.1.Сравнение предварительных θ 0 и конечных θ k значений обученности с исходным значением обученности θ

Общее поведение конечных значений обученности θk направлено на устранение отличий θ0 и θ, но эти изменения столь большие, что превышают различие θk и θ, даже приводят к изменению знака разности θk–θ, т.е. к неестественному поведению. Эта ситуация вызывает необходимость введения дополнительного фактора, уменьшающего эти изменения. Возможной причиной такого явления может быть, что статистическая выборка массивов испытуемых и заданий незначительна. Поэтому перенормируем поправочные коэффициенты (10) и (11), введя сигма-фактор по аналогии с эффектом Гиббса

Xa = X*σ                                   (17)

Yb = Y*σ                                   (18)

Как известно, эффект Гиббса проявляется из-за использования на практике усеченного ряда Фурье и исправляется умножением на фактор σ < 1 коэффициентов разложения.

Из условия наилучшего согласия конечных θ k с исходными

θ значениями

обученности определено значение фактора, равное σ = 0,7. Степень полученного согласия подтверждается критерием  χ2 (θk-θ) = 0,03 и демонстрируется на рис.2.

Теперь выберем задания повышенной трудности β1s=0,55, построив массив β1 при равномерном распределении 10 заданий на интервале β1= -3÷ 0 и 20 заданий на интервале β1= 0 ÷ 3. Результаты моделирования такого тестирования представлены на рис.3.

Повышенная трудность заданий понижает предварительную обученность группы от исходного значения θs = 0 до θ0s = -0,52 . Конечное значение обучен- ности, вычисленное на

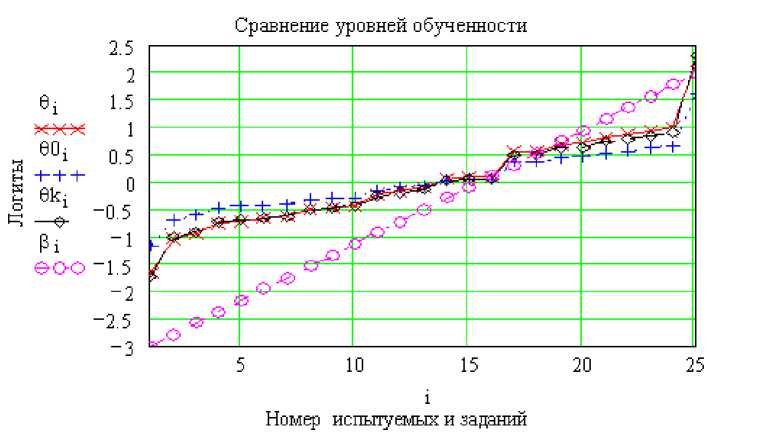
Рис.2 Согласие конечных

θ k

значений обученности с исходными

θ

при введении фактора σ = 0,7

основе вышеизложенной процедуры, с включением фактора σ = 0,7, равно θks = -0,03, что отлично согласуется с исходным значением (критерий χ2 (θk-θ) =0,06).

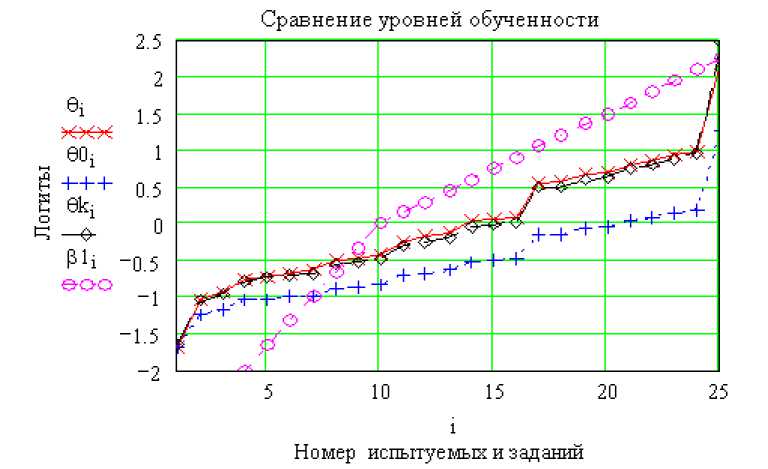
Рис.3. Cовпадение значений конечной обученности θk с исходной θ при обученности θs=0, трудности β1s=0,55 и σ=0,7

В реальности не часто встречается нормальное распределение обученности в академических группах. Поэтому рассмотрим случай, когда группа испытуемых имеет случайное распределение обученности. С этой целью используем стандартную функцию θ1 = runif(25,-2.5,2.5) и образуем массив из 25 случайных чисел в интер- вале (-2,5; +2,5) единиц логитов. Затем отсортируем этот массив по возрастанию значений обученности с помощью функции 91= sort(91).

Аналогично этому составим тестовые задания, трудность которых распределена так же по случайному закону pi= runif 30,-3,3) с интервалом (-3;+3), перекрывающим интервал обученности группы. Используя стандартную функцию случайных чисел, можно составить группы испытуемых с различным уровнем обученности и тесты разной трудности.

Численное значение о-фактора было проверено в нескольких вариантах тестирования с различным распределением обученности тестируемых и трудности заданий и с различной трудностью тестов. Определенное из условия наилучшего согласия параметров 9k и 9 по критерию х2, значение о-фактора оказалось одинаковым во всех вариантах тестирования. В дальнейших расчетах используется это установленное значение о=0,7.

Анализ результатов численного моделирования

Имея возможность создавать массивы со случайным распределением обученности 9 и трудности заданий в, выберем 3 группы испытуемых со средним уровнем обученности 9s ~ 0, 9s = - 0,2 и 9s = +0,2. Каждая группа многократно подвергалась тестированию. Средняя трудность es этих тестов варьировалась в пределах (-0,5; +0,5) логит. Тесты с трудностью выше этого предела не позволяют получить удовлетворительное согласие конечной обученности с исходной по критерию x 2 (9ks-9) .

На основе результатов этой серии тестирования изучался вопрос, как изменяется обученность 90s с возрастанием трудности теста es. На рис.4 представлена зависимость

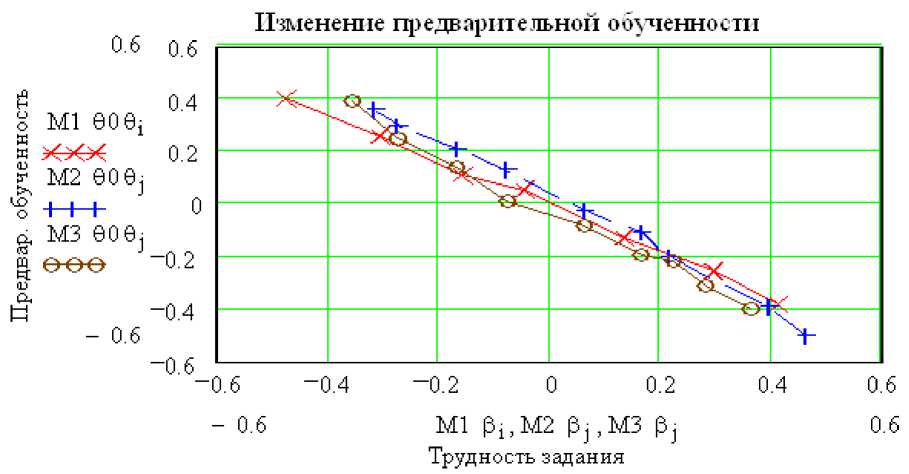
Рис.4. Понижение предварительной обученности группы 909s = 90s - 9s с ростом es трудности теста разности предварительной и исходной обученностей 909s = 90s - 9s от es -средней трудности теста. Массивы численных результатов тестирования 3 групп испытуемых обозначены М1, М2 и М3, соответственно. Эта зависимость оказалась линейной и не зависящей от исходной обученности группы. Вследствие этого, прямые отрезки θ0θs, соответствующие трем группам испытуемых, ложатся одна на другую.

Отметим, что при средней трудности теста βs ~ 0, т.е. при при компенсации трудных и легких заданий в тесте, предварительная обученность совпадает с исходной. Отсюда следует, что результаты тестирования с помощью теста компенсированной трудности βs ~ 0 дают достоверное оценивание знания без математической обработки их. При увеличении трудности теста оценка обученности группы линейно понижается, а при уменьшении трудности теста обученность возрастает.

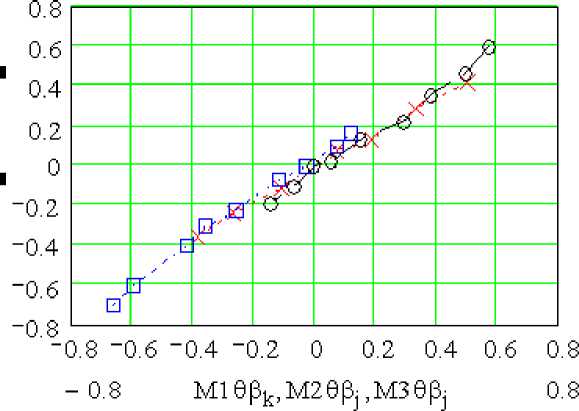
Но в реальности не достигается ни удачная калибровка тестовых заданий, ни достоверное шкалирование испытуемых. Поэтому необходимо проводить математико-статистическую обработку результатов тестирования для получения объективной оценки обученности. Степень согласия конечной обученности с исходной проверялась по критерию χ2(θk-θ) < 1, но не по соответствию средних значений обученности. Известно математическое свойство теста [7], которое заключается в том, что используемый для достоверной оценки обученности тестовый набор заданий с большим разбросом трудности (большая дисперсия) уменьшает разброс конечных оценок θk обученности. Вследствие этого усредненное значение конечной обученности контингента испытуемых оказывается в окрестности θks ~ 0. Это свойство не зависит ни от трудности теста, ни от начального уровня обученности испытуемых. Такая независимость (инвариантность) обученности от трудности теста демонстрируется на рис. 5, где данные серии тестирования с задниями разной трудности дают одинаковые результаты средней обученность 3-х групп испытуемых. Необходимо особо отметить, что тестовые оценки испытуемых совпадают с исходным уровнем обученности, что непрерывно контролировалось по критерию χ2 . Это свойство инвариантности указывает на объективность тестового контроля знания.

Модель Г. Раша обладает еще одной замечательной особенностью, связанной с относительной инвариантностью оценок обученности испытуемых и трудности заданий. Дело в том, что формула успеха (1) зависит только от разности параметров θ – β.

Если испытуемый выполняет задание трудностью β с некоторой вероятностью P(θ,β), то на задание трудностью β+c с прежней вероятностью ответит более подготовленный испытуемый с обученностью θ+c, так как θ – β = (θ + c) – (β + c). Этот эффект относительной инвариантности оценок параметров обученности и трудности отражен на рис. 6.

0.8

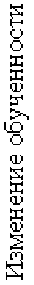
М190к

Х-ХХ

M260j

В-В В

M360j еео

- 0.8

Зависимость обученности от ра зности

I                        I

Разность обученности и трудности.

Рис.5. Инвариантность обученности относительно трудности теста.

к

и

Щ cd К F и

5 м

0.5

мт ekj

М2 9kj

М3 Skj

Инвариантность обученности от трл дностн

0.5                                                      '

0.4

0.3

0.2

0.1

О

-0.1

-0.2

-0.3

- 0.5-0.4

-0.5

-0.5     -0.3     -0.1

o.i

о.з

0.5

- 0.5

Ml pj,M2 pj ,МЗ pj Трудность теста

0.5

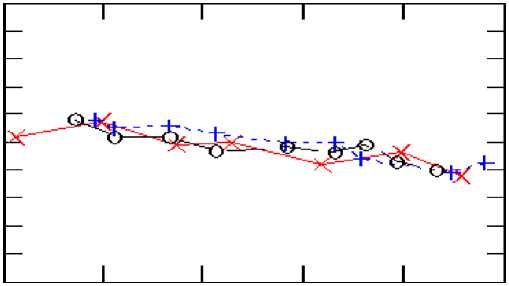
Рис.6. Иллюстрация относительной инвариантности средней обученности θ0s от разности средних значений параметров θβ=θs – βs.

Для всех 3-х вариантов тестирования наблюдается одинаковое линейное возрастание предварительной обученности с ростом разности параметров θs – βs . Совпадение средних значений θ0s в области, где перекрываются значения разности θs – βs для разных вариантов тестирования, дает обоснование для вывода об относительной инвариантности оценок параметров θ и β.

Заключение

Численным моделированием процесса тестирования в рамках модели Раша продемонстрировано, как математико-статистические методы современной теории тестов приводят к достоверным оценкам испытуемых, не зависящим от трудности заданий при выполнении необходимых требований проведения тестирования.

Одно из важных требований в том, что уровень трудности теста должен соответствовать уровню обученности испытуемых. Только в этом случае, когда близки средние значения трудности теста и обученности испытуемых, и достаточно велика дисперсия массива трудности задания, оценка обученности становится наиболее эффективной, которую можно принять в качестве объективной оценки. Сокращение интервала трудности заданий в тесте, т.е. уменьшение дисперсии массива заданий, приводит к снижению контролирующей функции теста.

Другое не менее важное требование состоит в том, что среднее значение массива заданий должно быть близко к βs =0, т.е. должно быть сбалансировано число трудных и легких заданий в тесте. В случае удачно компенсированной трудности βs ~ 0 теста достигается достоверное оценивание знания без дополнительной математической обработки их.

Только при выполнении требуемых условий проведения тестирования и профессиональной обработки его результатов достигается инвариантность оценок знания относительно трудности заданий.

В нашем численном моделировании процесса тестирования остается не выполненным требование достаточной статистики массивов испытуемых и заданий. В связи с внедрением в наших ВУЗах балльно-рейтинговой системы текущий контроль знания проводится по каждому модулю изучаемой дисциплины в отдельной академической группе с помощью тематических тестов, состоящих из ~30 заданий. В таких случаях модель Раша не всегда адекватно описывает эмпирические данные тестирования. И для согласования расчетных и исходных значений обученности вынуждены ввести поправочный множитель σ-фактор, причина которого возможна, что используемые статистические выборки заданий и тестируемых не значительны .

В заключение еще раз отметим, что достоверность оценки испытуемых достигается только в случае корректного проведения тестирования и профессионального анализа его данных в рамках модели Раша .