Численное моделирование инвазии популяций

Бюллетень науки и практики / Bulletin of Science and Practice

UDC 51-77                                          

Инвазия видов является угрозой биоразнообразию, функционированию экосистем. Вселение чужеродных видов оказывает отрицательное влияние на среду обитания реципиента. Инвазия активных видов в ареал может привести к вытеснению автохтонных видов, или к их уничтожению, существенно воздействовать на структуры и функции наземных и водных экосистем. Вселение, сопровождаемое вспышками размножения вида, приводит к возникновению множественных очагов массового размножения вселенца. Агрессивные виды могут наносить существенный экономический ущерб районам их вселения [1, 2].

Возникновение новых поселения человека, создание промышленных зон,

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №2. 2024 строительство транспортных магистралей приводят к фрагментации биоценозов. Это сопровождается уходом видов, проживавших на территории, и вселением новых видов. Окрестности промышленных зон и поселений человека заселяются видами, способными выдержать антропогенное давление.

Математическое моделирование позволяет оценить продолжительность заселения территории, распределение численности особей на территории и другие характеристики популяции. В исследованиях [3, 4] предлагаются модели, основанные на уравнениях в частных производных. В работе имитационное моделирование осуществляется на основе задачи Коши для системы обыкновенных дифференциальных уравнений. Заселяемая территория рассматривает как система последовательных зон, постепенно заселяемых популяцией.

Математическая модель вселенца

Освоение популяций свободных территории сложный процесс, вызванный различными причинами [5]. Одним из вариантов является распространение особей вдоль транспортных магистралей, водных путей, через зоны расположения трофических ресурсов [6-8]. На освоенных территориях возникает система поселений [9, 10], между которыми может происходить обмен особями.

Популяция, вселившаяся на новую территорию, постепенно начинает распространяться на ней. Всю территорию можно представить в виде системы последовательных n зон заданного размера [11]. Заселение начинается с первой зоны, по мере ее освоения часть особей освоенной зоны перемещаются в соседнюю зону, начинает ее осваивать. Модель заселения территории из n зон представлена системой дифференциальных уравнений du

— = -vu + F (Щ ) , du

— = -vu + vi-Ui-! + Fi (u),  (I = 2,...,n), где v — доля особей зоны i, переселяющихся в зону i +1, а F (u;) — собственная скорость роста численности популяции в зоне i . Емкости зон считаются разными, а удельная скорость роста численности популяции в зоне определяется качеством трофического ресурса.

К системе уравнений (1) добавляются начальные условия u = u , u = 0 ( i = 2,..., n ) , означающее, что освоение территории начинается с первой зоны, вселением в нее малого количества особей - uK , где K — емкость первой зоны.

Уравнение «освоения» первой зоны в (1) имеет стационарную точку и = 0 . Эта стационарная точка будет устойчивой, если выполняется условие

dF{ ( x )

dx

< v ,. То есть в

x = 0

том случае, если зону покидает большее количество особей, чем их «рождается».

В отсутствие миграции (при v = 0, i = 1,2,..., n ) собственные значения матицы Якоби правой части системы уравнений (1) в тривиальных стационарных точках подсчитываются по формулам Ai

dF. (u,)   /              х

- v + —   -  ( i = 1,2,..., n ) .

du

С учетом этого при выполнении неравенств

dFi ( ^ui )

du

N i = 0

> V i

тривиальная стационарная

точка будет неустойчивой. Поэтому заселение территории в модели (1) может происходить при медленном ее освоении (при малом количестве уходящих особей). Этот результат согласуется с полевыми наблюдениями за заселением границ ареала [12].

Для случая логистической популяции система уравнений (1) принимает вид du dt du dt

- vu + ^u (1 - u),

^- vu ⁺ v - ^ui - 1

u

⁺ A ^ui ^{1 -}~ ,   ^{( 1} = ^2,

n ) .

В этой модели предполагается, что минимальную емкость имеет первая зона, и ее емкость принята за единицу измерения. Емкости остальных зон считаются большими, чем емкость первой зоны: 1 <  K_i для i = 2,..., n .

Правая часть первого уравнения в (2) будет отрицательной при любых положительных значениях u , если выполняется неравенство v >  щ . В этом случае со временем во вторую зону особи из первой зоны мигрировать перестанут. И если для остальных зон в этом случае будут выполняться неравенства v >  щ ( i = 2,..., n ) , то заселение территории не состоится.

Стационарное значение численности популяции в зоне i (i = 2,...,n) находится как ui

положительный корень уравнения - v i u i + v i - u i - 1 + u u i

= 0.

-

При выполнении неравенств 0 <  v^u^ это квадратное уравнение будет иметь положительный корень.

Решение системы уравнений (2) осуществлялось в среде программирования математического пакета Matlab с применением встроенных функций. На Рисунке 1 для 50 зон приведен вариант распределения времени начала освоения логистической популяцией 5 0-ой зоны для случая параметров выбранных из диапазонов v е (0.002,0.02) , щ е (0.03,0.08) , K е (1.0,2.0) случайным образом для N = 1000 вариантов.

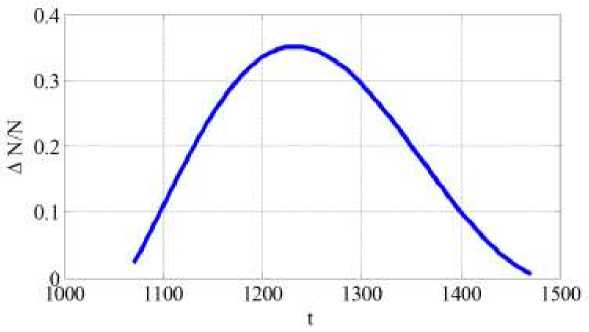
Рисунок 1. Распределение промежутка времени начала заселения последней зоны

Таким образом, логистическая популяция последовательно может заселить несколько ближайших ареалов. При этом временной интервал заселения последней зоны описывается распределением, близким к нормальному распределению.

Модель вселения двумя группировками

Заселение территории может происходить несколькими группировками особей [3, 5]. Для случая двух группировок предполагается, что каждая из них заселяет свои зоны расположенные «параллельно». Так что может происходить обмен особями между двумя соседними зонами. У каждой из n зон своя емкость, свое качество трофического ресурса. Линейная скорость передвижения особей у группировок считается разной. Доля особей переходящих из одной группировку в другую различная.

Пусть в каждой из группировок u и w численность особей в своей зоне с номером i - u и w , емкости зон — K и K , скорости перехода из зоны в зону — v и v , удельные скорости роста численности популяций — ц и ц , доля особей переходящих из группировки u в группировку w - d , а из группировки w в группировку u - d .

Заселение начинается с первой зоны. По мере ее освоения часть особей освоенной зоны перемещаются в соседнюю зону, и начинает ее осваивать. Модель заселения территории представлена системой дифференциальных уравнений

Ли           .                     1       ,                                           (3) — = — Vu 1 и 1 + А и 1 и 1 1 — —-- du 1 и 1 + dw 1 W 1 , dt                1    Ки 1 J d W             f1   W — = — vw 1 W 1 + A w 1 W 1 1 — — + du 1 и 1 — dw 1 W 1 , dt                 I    K w 1 J dUi                          f,    и ^           ,                                         (4) — = Vui - 1 и — — KUi + A ui u i 1 — —-- duiUi + dwiwi , dt                       l    K ui J dw                     f,   w Y , — = Vwi — 1 wi — 1 — Vwiwi + A w 1 w 1 — — + d ui u i — dwiwi , dt                          l    K wi J ( i = 2,..., n ) .

К этим уравнения добавляются начальные условия

U (0) = и 0 ,   W j (0) = w₁ 0 ,

U (0) = 0, w (0) = 0,      ( i = 2,..., n ) .

В стационарной точке и = 0, w = 0 матрица Якоби правой части уравнений (3)

—v , + ц , — d ,         d , и 1 uii 1       и 1                    w1

d i           —v i И- д i — d i , и 1              W1   Aw 1     w 1 J при одновременном выполнении неравенств

Ги 1 < vu 1 и Aw1 < vw1 , или Ци 1 < Vu 1 и rw1 < dw1 , или Ци 1 < du 1 и rw1 < vw1 ,

ИЛИ Ц и 1 <  ^du 1 и r w1 <  ^dw1

будет иметь собственные значения с отрицательной вещественной частью.

Соответственно тривиальная стационарная точка будет устойчивой. То есть при скорости роста численности группировок в первой зоне меньшей любой скорости парной миграции особей группировки покинут первую зону.

В зону i поступают особи из группировок зоны i — 1. Поэтому, поскольку в этом случае 0 <  Vm-Ui-i и 0 <  v_wi-Wi- 1, тривиальная точка в этой зоне не реализуется. То есть модели (1) и (3)-(4) прогнозируют наличие во всех, кроме первой, зонах присутствие особей группировок. Плотность заселения зон u / K_i ( i = 1,2,..., n ) в общем случае неравномерная. «Незаполненным» зонам соответствуют значения u / K_t<  1, а «переполненным» u_t / K >  1. Такое распределение объясняется неоднородностью миграции особей.

На Рисунке 2 для 50 зон приведен вариант распределения плотности особей первой группировки логистической популяции в зонах для случая параметров выбранных из диапазонов ( v _u , v _w ) е (0.01,0.0) , ( _А ,^ ) е (0.2,0.2) , ( K_u , K_w ) е (1.0,2.0) , ( d_u , dv_w ) е (0.05,0.10) случайным образом для N = 1000 вариантов. Вертикальной пунктирной линией отмечена граница между «незаполненными» зонами ( u / K <  1 ) и «перенаселенными» (1 <  u / K ). Распределение для обеих группировок с точностью не более 10% совпадают. Такой подход в имитационном моделировании позволяет на основе анализа прогностических данных модели с учетом реальных экспериментальных данных принять рациональное управленческое решение [13].

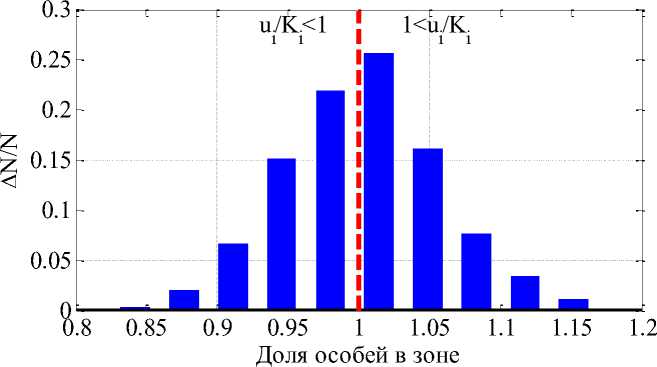
Рисунок 2. Распределение плотности заселения ареала

Освоение популяцией свободной зоны несколькими группировками может сопровождаться повышенной плотностью населения на одних участках, пониженной на других. То есть модель (3) – (4) предсказывает неравномерную плотность населения на вновь освоенной территории.

Численная реализация решения задачи Коши для систем дифференциальных уравнений осуществлялась в среде программирования математического пакета Matlab. Интегрирование осуществлялось с применением встроенных функций и модулей [14].

Наиболее рациональной является функция ode45. Точность численного решения составляла не менее 10-6 как в абсолютных, так и относительных отклонениях. Векторизация вычислений позволяет ускорить построение численного решения. На временном интервале

1 000 единиц времени решение системы 100 дифференциальных уравнений не превышало одной минуты.

Заключение

Разработанные модели вселения популяции в новый ареал объясняют неравномерную плотность заселения участков различной емкости и качеством трофического ресурса. Это относится как к популяциям, осваивающими территорию как всей популяцией в целом, так и ее отдельными группировками. Основной принцип закрепления популяции на новой территории – скорость роста численности популяции на всех участках обитания должна превосходить скорость уходя части особей с осваиваемых участков.