Численное моделирование извержения вулкана ЭТНА с применением усредненной по глубине модели потока лавы

Магма представляет собой сложную смесь, которую образуют расплавы большого числа соединений, кристаллы, пузырьки разных газов и водяной пар [1, 2] . При выходе на земную поверхность магма теряет воду и другие летучие вещества, остывает и становится лавой. Лава — это гравитационные потоки частично расплавленной породы, которые неравномерно охлаждаются при течении, постепенно затвердевают и прекращают свое продвижение.

Модели течения лавовых потоков, обсуждаемые в данной работе, учитывают влияние тепловых, кинетических и реологических факторов на динамику распространяющейся лавы. Температура растекающейся по подстилающей поверхности лавы меняется под влиянием таких физических факторов, как диффузия и перенос вещества внутри потока; перенос тепла с поверхности лавы в окружающее пространство или в лежащую под ней почву; радиационное излучение энергии с поверхности лавы в окружающую среду; выделение энергии за счет вязкого трения и фазовых переходов. Высвобождение водяного пара из расплава вызывает значительные изменения реологических свойств потока. Неровности подстилающей поверхности, неустойчивости, возникающие в результате охлаждения и дегазации лавы, способствуют разветвлению потока, образованию складок, рифтов и трещин, формированию на поверхности лавы других особенностей ее внешнего вида. При относительно устойчивых условиях извержения, то есть при непродолжительных выбросах газово-пепловой смеси под большим давлением, вязкий поток быстро приобретает твердую корку за счет радиационного и конвективного теплообменов с внешней средой. Кристаллизация самого верхнего слоя движущегося расплава приводит к гравитационному течению под твердой коркой, которая изолирует жидкую лаву от быстрого охлаждения и позволяет ей распространяться на значительные расстояния. После прекращения подачи лавы ее внутренняя часть постепенно охлаждается и поток останавливается.

Существует три основных типа вулканической магмы: базальтовая, андезитовая и риолитовая, которые различаются не только минеральным составом, но и объемными долями компонентов. Так, содержание кристаллов у магмы в жерле вулкана составляет от 5% во многих базальтах и риолитах, до 30^50% в андезите. С удалением от вулканического жерла содержание кристаллов в лаве увеличивается до тех пор, пока не достигнет некоторого равновесия. Этот процесс описывается кинетическим уравнением роста доли кристаллов в расплаве [3].

Динамическая вязкость лавы определяется ее химическим составом, степенью кристаллизации и температурой. Реологию лавы обуславливают ее фактическая вязкость, которая зависит от динамической вязкости, и нелинейная связь между напряжением сдвига и скоростью деформации [1] . Приближением, которое часто используется для моделирования реологии лавы, является закон Бингама [4] . Жидкость Бингама — это простейшая аппроксимация пороговых жидкостей: такие жидкости покоятся, пока приложенные напряжения сдвига (вызванные, например, гравитационными силами) остаются меньше предела текучести. Как только предел текучести преодолевается, жидкость течет со скоростью потока. Предел текучести допускает эффект стойкой корки, которая останавливает поток, когда он становится слишком тонким для моделирования. В процессе остывания в расплаве растет содержание кристаллов; они начинают взаимодействовать между собой, увеличиваются в размерах, создают сложные структуры. В случае сдвига нелинейная связь между напряжением и скоростью деформации описывается с помощью соотношения Гершеля–Балкли [5] , которое является комбинацией степенного закона и закона Бингама.

При учете длительности извержения и времени распространения потоков реологические свойства лавы могут быть неоднородными. Магма, выходящая из кратера, не имеет значительного предела текучести до того, как произойдет охлаждение и кристаллизация. Далее, по мере приближения температуры потока к солидусу, все большее влияние на свойства лавы оказывают нелинейные эффекты [1] .

Одна из задач в области охраны окружающей среды заключается в предсказании чрезвычайных ситуаций, оценке рисков извержений и их последствий [6] . Для этого большое значение имеют данные наблюдений, знание термических и динамических свойств потоков лавы. Компьютерное моделирование, ставшее неотъемлемой частью исследований в этой области, использует для описания соответствующих природных процессов модели, в которых характеристики процессов являются основными параметрами.

Моделирование играет важную роль в понимании структуры потока лавы, его морфологии и тепловой эволюции [7, 8] . Работа [8] представляет обзор численных подходов и программных средств для изучения потока лавы. На сегодняшний день программные продукты для этих целей делятся на две категории: способные обеспечить вычисления в режиме реального времени и адекватно изображающие сложную структуру лавовых потоков в объемной области. К первой категории относятся: модели потока лавы, осредненного по глубине; модели стохастической маршрутизации; модели клеточных автоматов [9 –11] . В целом эти модели опираются на простой набор правил (иногда не следующих непосредственно из физических законов) для расчета распределения вязкой среды. Вторую категорию образуют модели вычислительной гидродинамики — Computational Fluid Dynamics (CFD) [12, 13] , и гидродинамики гладких частиц — Smooth Particle Hydrodynamics (SPH) [14] , реализованные в пространственных областях. Эти коды работают достаточно медленно, но позволяют детально учитывать неоднородные структуры потока.

Математические модели лавовых потоков, основанные на усредненных по глубине 3D уравнениях Навье–Стокса для несжимаемой вязкой сплошной среды, разработаны в [7, 15] . При их реализации результаты получаются довольно быстро, но такие модели имеют ограничение, заключающееся в том, что физические параметры среды (скорость, вязкость, температура и другие) не меняется по глубине потока. Это не позволяет принимать во внимание неоднородности течения по вертикали, например, эволюцию образования твердой корки на поверхности потока вследствие фазовых переходов в расплаве. Но, несмотря на это, данные модели являют собой удачный компромисс между физической точностью и скоростью вычислений.

Данное исследование подразумевает совместное решение уравнений, составляющих модель, таких как: уравнения для глубины лавы и скорости ее распространения; уравнения, описывающие кинетику кристаллов; уравнения теплового баланса, учитывающие нелинейный конвективный и радиационный обмен энергией с внешней средой, энергию диссипации и скрытую теплоту кристаллизации. Реологию лавы представляют нелинейные зависимости фактической вязкости лавового потока от температуры, скорости сдвига, предела текучести (предел текучести и степень нелинейности (или степенной индекс) также являются функциями температуры). Приводятся некоторые предварительные результаты применения модели к изучению реологии лавовых потоков.

Задача на базе сформулированной модели реализована в пакете OpenFOAM с открытым исходным кодом, что позволило использовать современные высокопроизводительные вычислительные кластеры и легко адаптироваться к конкретным физическим аспектам рассматриваемого природного процесса. Проведена верификация кодов путем сравнения аналитического решения задачи с тестовым решением на основе модели с уравнениями движения двухфазной жидкости в объемной области. Исследовано влияние на поток реологических характеристик при его описании моделью Ньютона по сравнению с моделью Бингама и нелинейной моделью Гершеля–Балкли. При этом в представление реологии жидкости включены не только нелинейные зависимости фактической вязкости лавового потока от температуры, скорости сдвига, предела текучести, но и зависимости от температуры как самого предела текучести, так и степенного индекса. Параллельные компьютерные коды реализованы с помощью интефейса OpenMPI на вычислительных кластерах с общей и распределенной памятью под управлением ОС Linux. Проведено профилирование кодов для многоядерных процессоров с общей памятью. Расхождение между результатами компьютерного моделирования и данными наблюдений дает направления для дальнейших исследований и совершенствования приемов описания реологических закономерностей лавовых потоков.

• 2.    Постановка задачи

Многие геофизические и вычислительные проблемы течения вязкой несжимаемой жидкости возникают при рассмотрении процессов в очень больших пространственных областях, для которых детальное трехмерное моделирование гидродинамики не является эффективным, поскольку отношение вертикального размера потока к его горизонтальному размеру очень мало. К таким задачам можно отнести сход снежных лавин и селевые оползни, распространение в океанах цунами и приливных волн. При этом математическая модель, как правило, основывается на усредненных по глубине потока жидкости (среды) уравнениях, полученных путем интегрирования по вертикальной переменной и упрощения трехмерных уравнений Навье–Стокса для несжимаемой сплошной среды.

Li

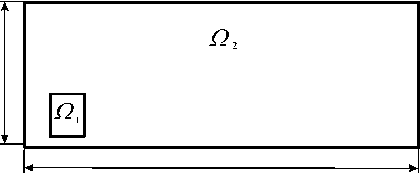
Рис. 1. Расчетная область Р = Р 1 U Р 2 = (0 ,L 1 ) х (0 ,L ₂ )

Рассмотрим процесс вытекания вязкой несжимаемой жидкости из кратера вулкана и сформулируем его. математическую модель. В качестве основных уравнений состояния жидкости примем двумерные усредненные по глубине потока уравнения движения вязкой жидкости. В модельной области О = (0,L ₁ ) х (0,L ₂ ), О = О U О ₂ (Рис. 1) на промежутке времени t е [0,0], где t = 0 — конечный момент времени наблюдения за процессом, движение представляется системой дифференциальных уравнений в частных производных и соответствующими

начальными условиями [7, 16, 17]: ∂h — + V-(hu) = win, x е J/, (1) L )+ v^(huu)=      (gh2) gh     yu, xе/2, dt                 2 dxy '     dx (2) (h.)+v(hvu)= „ ^ (gh2) gh ~ yv, xe О,, dt            2 dy^'dy (3) h(0;x,y) = 0,  u(0;x,y) = 0, v (0;x,y) = 0, x е О, (4) где x = (x,y) — декартовы координаты точки на плоскости, h = h(t;x,y) — высота столба жидкости, измеренная от уровня подстилающей поверхности H = H(x,y) до поверхности взаимодействия жидкости с окружающей средой (до свободной поверхности жидкости), u = u(t;x,y) = (u = u(t;x,y),v = v(t;x,y)) — вектор усредненной по глубине потока лавы скорости жидкости в момент времени t е [0,0] в точке x = (x,y) е О:

H ( ^x, y) + ^{h ( t} ;x,y)

u (t;x,y ) = h ¹ (t;x,y )

!

U (t;x,y,z)dz.

H ^{( x,}y)

Здесь U = U(t; x,y,z ) — вектор скорости потока жидкости; w in — магнитуда скорости экструзии жидкости (w in = w in (t; x ) > 0, если x е О; w in = 0, если x е ^ ₂ ); y = Y (t; x ) — коэффициент сопротивления, в котором учитываются реология жидкости, свойства самого потока и взаимодействие с подстилающей поверхностью; g — ускорение свободного падения.

Уравнение сохранения энергии для усредненной по вертикали температуры

H(x,y)+h(t;x,y)

T (t;x,y) = h ¹ (t;x,y)

I

T (t;x,y,z)dz,

H(x,y)

где T = T(t;x,y,z) — температура жидкости, запишем как

Cpi^dT ⁺ ^T ^M) = Q™ d ⁺ Q conv ⁺ Q diff ⁺Q diss ⁺ Q lat , X G ^ (5)

Q rad = -™. f ( T ⁴ - Thr ) , Q conv = -K ir f (T -T air )^ , Q dif f = ^diff h ^- T - T^f ) ,

Qdiss = mh-1M^u^2- Qlat = T-1 L^P^eq -■h, с условием T(t;x) = Tin(t;x), x G ^1 при t > 0 для температуры на поверхности кратера и начальным условием T(t = 0,x)= Tair(x), XG ^2. При этом Tair — температура внешней среды, а — константа Стефана-Больцмана, ε — коэффициент излучения, λair — коэффициент теплопередачи в атмосферу; скобки ⟨ ⟩ обозначают скалярное произведение векторов. Величина f = f (t;x) G [0,1] определяет долю покрытия жидкой лавы твердой коркой. Если f = 1, то это означает отсутствие корки в данном месте потока [18]. Как показывают численные эксперименты [19], расчетная толщина лавовой корки увеличивается, если в модели учитываются нелинейный конвективный и радиационный теплообмены; при увеличении скорости потока лавы и изгибах рельефа корка истончается и может разрываться.

Члены в правой части уравнения (5) представляют радиационный — Q rad , нелинейный конвективный — Q conv , и кондуктивный — Q diff , теплообмены [20] . Два последних члена — Q diss и Q lat , описывают выделение тепла за счет вязкой диссипации и кристаллизации. Здесь n dif f , m — эмпирические параметры; T dif f — температура раздела на границе лавы и грунта; µ — динамическая вязкость; c — удельная теплоемкость; ρ — плотность; k — коэффициент теплопроводности; L ∗ — коэффициент скрытой теплоты фазового перехода; ϕ — объемная доля кристаллов; ϕ _eq — доля кристаллов в равновесном состоянии.

Часто тепловая модель предполагает постоянство коэффициента излучения ε как для расплавленной лавы, так и для охлажденной корки (обычно он принимается равным 0.9). Однако лабораторные исследования показали, что коэффициент излучения увеличивается нелинейно с охлаждением и обнаруживает значительно более низкие значения, чем обычно считается. В частности, анализ образцов лавы извержения Этны 2001 года в диапазоне температур от 773 до 1373 К показал, что коэффициент излучения ε зависит от температуры. Это приводит к различиям до 20% в конечном расположении моделируемых потоков лавы [21] . Установлена эмпирическая зависимость, связывающая этот коэффициент и температуру лавы [22] :

e(T ) к 0.976716+4.08881 ^{- 5} T - 1.9506210 — 7 T ² .

Объемная доля кристаллов ϕ , усредненная по глубине, в потоке лавы определяется из эволюционного уравнения, описывающего упрощенную кинетику роста содержания кристаллов при кристаллизации, вызванной дегазацией:

■ + (V ( h_A u ) =            ■   . x G « 2 -

∂t                         τ с условием ■(t;x) = ■in (t;x), x G «1, при t > 0 для объемной доли кристаллов на поверхности кратера и начальным условием ■(t = 0,x) = 0, x G «2. Здесь объемная доля кристаллов в равновесии ■eq = ■eq(T,p) зависит от доли водяного пара в лаве, растворенной в магме (это учитывается за счет внутреннего давления p в лаве), и от температуры; τ — время релаксации кристаллов. При предположении, что содержание растворенной воды постоянно при давлениях, близких к атмосферному, в модели используется зависимость ϕeq от температуры вида [23]:

■ eq ( Tc ,p к 10 ⁵ ) = 1/ ( 1+exp [ a i + b i T c /T sp +c i (T c /T sp)²]) ,                      (8)

где Tc — температура лавы, [°C], a ₁ = - 42.4, b ₁ = 51.04, c ₁ = - 11.11, T _sp = 1000 °C.

• 3.    Реология жидкостей

В применяемой модели фактическая вязкость лавы зависит от температуры и скорости сдвига [3, 24] : g = g(T,e), где e = | V u+ V u T | — второй инвариант тензора скоростей деформации. Динамическая вязкость лавы — функция температуры и содержания водяных паров в расплаве; для ее расчета в лабораторных экспериментах для вулкана Этна получена формула [25] :

lg(g_D (T)) = - 4.643+ ⁵⁸¹².^{44 - 42}7.0^4W ,                             (9)

D             T-499.31+28.74lnW, где T — температура лавы, [К], W — содержание водяного пара, [%]. Зависимость будет рассматриваться в диапазоне температур 800+1350 К, где граничные значения означают минимум /id (800) и максимум gD (1350).

Закон Бингама является простейшей аппроксимацией поведения пороговых жидкостей. В этом случае поток может характеризоваться фактической вязкостью, которая представляется в виде: ^eff = /j, + т ₀ е ^-1 . Таким образом, при небольших скоростях деформации предел текучести может привести к фактической вязкости, которая намного превышает динамическую вязкость жидкости. Тогда параметр сопротивления среды y , [м ^ с ^{- 1} ] можно записать в виде [15] :

Yb = Р-1(то/11и11+3м/Н где g — динамическая вязкость, ([Па^с]), вычисляемая по формуле (8), р — плотность, [кгм-3], т0 — предел текучести, [Па]. При т0 = 0 получаем ньютоновскую жидкость и yn = 3^h-1 р-1.

В работе [26] установлена зависимость предела текучести от температуры:

lgT ₀ = 13.00997 - 0.0089T.                                     (10)

В диапазоне температур от 800 до 1400 К предел текучести изменяется от 1 до 10 ⁶ Па. Некоторые экспериментальные зависимости предела текучести от содержания кристаллов в лаве, ее морфологических параметров и геометрии подстилающей поверхности приведены в работе [27] .

Реология Гершеля–Балкли является обобщением реологии Бингама и степенного закона. В этом случае поток характеризуется фактической вязкостью ^ eff , которая представляется в виде ^ _e ff = ^ K e n ^{- 1} + т ₀ е ^-1 , где степенной индекс n = n(T). Аналогично при небольших скоростях деформации фактическая вязкость может намного отличаться от коэффициента густоты потока ^ K , [Па< ^п ]. Во всех потоках, кроме небольших, наблюдаются локальные разрушения поверхностной корки под воздействием тепловых нагрузок и течения, что приводит к образованию в потоке жидкой лавы блоков из твердых плит, которые могут наползать друг на друга и образовывать дамбы.

Зависимость степенного индекса n от температуры найдена с помощью лабораторных экспериментов и аппроксимирована формулой [28] :

n(T ) = - 0.35+0.85 x 10 ^{- 3} T.                                    (11)

Таким образом, из решения системы (1) – (7) с учетом (8) – (11) в расчетной области на требуемом отрезке времени необходимо определить поле скоростей, глубину лавы, температуру и содержание кристаллов в лаве.

• 4.    Тестирование решателя и верификация кодов

Для оценки применимости метода численного решения системы (1) – (4) проведен тестовый эксперимент на решении задачи растекания фиксированного объема первоначально заключенной в цилиндр жидкости c вязкостью µ и плотностью ρ с целью сравнения полученного профиля ее течения с аналитическим решением задачи течения жидкости по горизонтальной поверхности. Существует аналитическое решение данной задачи в случае тонкого слоя жидкости (Рис. 2а ) [29] . При рассмотрении осесимметричного случая уравнение для профиля растекания представляется как

h(R,t) = ^³№ц/ЫУ)^{1 / 4}^/^ ),

1 ^{/ 8} , ^n = ( 1024/ ( 81п ³ )) 1 ^{/ 8}

здесь h — высота слоя жидкости; R — радиус растекания; £(R,t) = R(pgQ³t/3p^

~ 0.894 — значение £ в формуле для положения фронта растекания R = R N (t) = £ N ( pgQ 3 t/(3^) ) 1 ^{/ 8} ;

R N ( t )

Q = 2п У Rh(R,t)dR — объем жидкости; ^(z) = ( 3 ( 1 - z ² ) /16 ) 1 ^{/ 3} . Формула (12) выведена в приближении 0

тонкого слоя, что соответствует тестируемой модели. Первоначальные высота и диаметр цилиндра равны 1 м (см. Рис. 2б ). В данном эксперименте приняты следующие значения модельных параметров: вязкость ^ = 10 3 Па<; плотность р = 2600 кгм ^{- 3} .

Для сравнения с аналитическим решением (12) взят момент времени t = 4 c (Рис. 2в ). Момент выбран с учетом того, что жидкость уже растеклась достаточно и верхняя граница исходного цилиндра жидкости исказилась. При этом его высота не обратилась в нуль.

Рис. 2. Аналитическое решение (12) (сплошная линия) и модельное решение задачи (1) – (4) (пунктирная линия) ( a ); начальное состояние столба жидкости ( б ); состояние жидкости в момент времени t = 4 ( в )

Далее сравним процесс растекания в модели (1) – (4) с движением вязкой несжимаемой жидкости в рамках модели эволюции многофазной несжимаемой жидкости в поле силы тяжести в пространственной области по заданному рельефу. Одну фазу такой жидкости представляет собой собственно вязкая несжимаемая жидкость, другую фазу — несжимаемая жидкость с малой плотностью и малой вязкостью, которую условно будем называть воздухом. Математическая модель эволюции включает в себя уравнения Навье–Стокса в пространственной области, несжимаемости, переноса вязкой фазы, а также соответствующие начальные и граничные условия. Подробно эта модель описана в [12] . Воспользуемся модификациями решателя OpenFOAM, а именно multiPhaseInterFoam, который моделирует движение многофазной несжимаемой жидкости в поле под действием внешних сил и сил межфазного взаимодействия, и nonNewtonianIcoFoam, в котором реализован SIMPLE алгоритм совместного расчета поля скоростей и давления, общих для всех фаз несжимаемой жидкости.

Модельная область имела размеры ^ OF = [0,500] х [0,500] х [H (x 1 ,x ₂ ),H(x 1 ,x ₂ )+20] м ³ и включала в себя кратер со спутниковыми координатами (x 1 =500316 м, y 1 =4177709 м, r 1 = 15 м, v 1 =0.017927 м - с ^{- 1} ). Снизу и сверху область ограничивалась рельефом исследуемой местности H . Гексаэдральная расчетная сетка создавалась утилитой blockMesh на основе предварительно подготовленного файла blockMeshDict с координатами узлов и границ. Сетка состояла из 100 х 100 x 25 гексаэдральных ячеек. Среднее число неортогональности равнялось 20 градусам. Технические детали построения сетки описаны в работе [30] . Были приняты следующие значения модельных параметров: вязкость ^ =10 5 Па - с, плотность р = 2500 кг - м ^{- 3} .

На рисунке 3 демонстрируются контуры растекания жидкости в момент времени 5700 с. Сплошная линия отвечает модели (1) – (4) , точечная — границе между лавой и воздухом в рамках двухфазной модели эволюции движения.

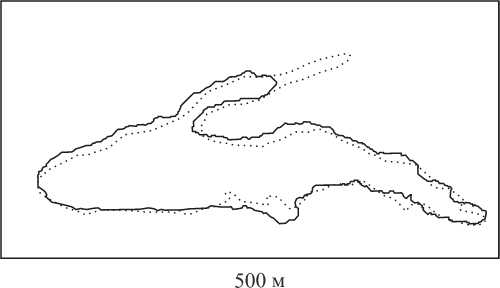
Рис. 3. Растекание жидкости в модели (1) – (4) (сплошная линия) и в рамках двухфазной модели движения (точечная линия)

• 5.    Численная реализация модели в пакете OpenFOAM

Пакет OpenFOAM (Open Source Field Operation And Manipulation) предназначен для численного решения дифференциальных уравнений с частными производными в произвольных пространственных областях. Он представляет собой набор библиотек программ на языке С++ и управляется операционной системой Linux. Основным преимуществом OpenFOAM является открытый исходный код, который позволяет быстро адаптировать модельные прототипы к реальным задачам.

Рис. 4. Рельеф H ( x ) доступен в открытом доступе [31] в виде цифровой модели рельефа DEM

Рельеф местности (подстилающая поверхность) обычно доступен как цифровая модель рельефа (DEM) в виде регулярной двумерной сетки (Рис. 4) . OpenFOAM имеет широкий спектр инструментов для создания (импорта) и преобразования сетки. Качество сетки оказывает непосредственное влияние на качество расчетов. Регулярная ортогональная сетка в прямоугольнике (см. Рис. 1) для модели (1) – (4) строится утилитой blockMesh . Далее данные из 3 столбца DEM файла формируют функцию H , количество строк и их порядок в DEM файле соответствует параметрам, указанным в файле blockMeshDict .

Распараллеливание счета в OpenFOAM достигается средствами самого пакета, который включает в себя MPI (Message Passing Interface) для создания независимых друг от друга вычислительных процессов, число которых ограничивается только ресурсами ЭВМ. Организация таких процессов заключается в распределении узлов расчетной сетки между ними. На рисунке 5 демонстрируется время расчетов с использованием явной и неявной схем решения систем алгебраических уравнений (СЛАУ). Расчетная сетка в данном тесте содержала ∼400000 ячеек. Сплошной заливкой обозначена доля ресурсов на получение СЛАУ и их многократное решение. Основная временная нагрузка при явной схеме приходится на аппроксимацию дифференциальных операторов. При количестве ядер N> 16 решатели СЛАУ и модули программы аппроксимации дифференциальных операторов берут на себя загрузку процессора примерно поровну. На рисунке 6 показано ускорение расчетов при явной схеме интегрирования уравнений (1)–(3), (5), (7) в зависимости от числа используемых ядер. Расчетная сетка в этом тесте состояла из ∼1600000 ячеек. Общее количество ядер в расчетах ограничивалось числом 36 — максимальным количеством ядер на одном узле ЭВМ, которые имеют общую оперативную память. При необходимости увеличения ресурсов расчет будет осуществляться на нескольких узлах ЭВМ, что значительно снизит эффективность расчетов, так как будут учитываться затраты на межпроцессорные обмены. В системах с общей памятью несоответствие между скоростью процессора и скоростью обменов с памятью всегда является основным узким местом для объема операций, которые могут быть выполнены за заданное время: медленная подкачка данных из оперативной памяти не может обеспечить процессор нужной информацией. Расчеты проводились на OpenFOAM-7, gcc(64) версии 8.3 на двух 18-ядерных процессорах Intel Xeon Gold 6254 CPU 3.10GHz с общей оперативной памятью 64 Гб.

В пакете OpenFOAM для аппроксимации дифференциальных уравнений в частных производных используется метод конечных объемов [32] — сеточный метод, при применении которого вычислительная область делится на ячейки, образующие объемную сетку. Ошибка численного решения задачи оценивается при этом как O(d q ), где d— размер ячейки, а q обозначает порядок точности численной схемы [33] . Очевидно, что для уменьшения ошибки вычисления необходимо либо уменьшить размер ячейки, либо увеличить порядок точности вычислительной схемы. Уменьшение размера ячеек приводит к увеличению размерности дискретной задачи и уменьшению шага по времени, что влечет за собой нелинейный рост продолжительности счета. Применение аппроксимаций высокого порядка точности имеет следствием появление неустойчивости численного решения и искажение основных физических законов в получаемых результатах. При реализации вычислений невозможно априори узнать, как создать сетку с минимальным числом ячеек, удовлетворяющую допустимой погрешности вычислений.

Метод динамической перестройки сетки в зависимости от результатов анализа одной из компонент находимого решения реализован в OpenFOAM. Однако качество аппроксимации дифференциальных операторов при этом становится хуже, так как число неортогональности сетки возрастает. При распределении узлов между процессами исходя из геометрии сетки нарушается сбалансированность раздачи информационной нагрузки на вычислительные узлы ЭВМ, что снижает эффективность расчетов. Сетку можно сгущать статически и выделять зоны, которые

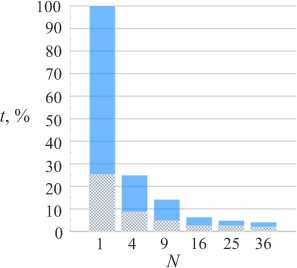
Рис. 5. Времена расчетов t = ( t N/1 1 ) х 100 %, t _N -время счета на N ядрах процессора по неявной (сплошная заливка) и явной (штриховка) схемам интегрирования системы (1) – (3) , (5) , (7) ; размер расчетной сетки ^ 400000 ячеек

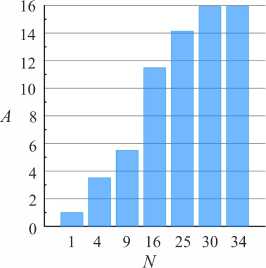
Рис. 6. Ускорение расчетов A = t 1 /-t N , t _N -время счета на N ядрах процессора по явной схеме интегрирования уравнений (1) – (3) , (5) , (7) в зависимости от числа используемых ядер процессора; размер расчетной сетки 1600000 ячеек

фактически не участвуют в получении решения. В пакете есть инструменты, которые позволяют удалять из рассмотрения соответствующие ячейки сетки и сокращать размерность задачи (а значит, и время расчета). Если задача требует многократного решения вследствие варьирования параметров в модели, то имеет смысл сделать расчет на грубой сетке, а затем сгустить сетку и удалить из нее ненужные зоны средствами пакета.

Обработка и визуализация результатов моделирования в OpenFOAM выполнены с помощью графического пакета ParaView с открытым исходным кодом [34] . Им можно считывать и визуализировать файлы из OpenFOAM и использовать их для дальнейших операций.

• 6.    Модельный пример

  В работе [31] приведены данные об извержении, которое произошло на горе Этна 6 ^ 8 декабря 2015 года у Нового юго-восточного кратера (NSEC), самого молодого из кратеров на вершине Этны. Информация, полученная со спутников, включает оценку скорости извержения и вулканических отложений (которые состоят из горных пород и газов), морфометрические параметры отложений и лавовых потоков (площадь распространения лавы; ее максимальная длина, скорость распространения и объем). В частности, лава заняла площадь 5.14 х 10 6 м ² и достигла длины примерно 4 км (Рис. 7a ). Минимальная, средняя и максимальная глубины лавового потока оцениваются, соответственно, как 1.0, 4.82 и 5.31 м. За 48 часов извержения объем вытекшей лавы составил 2.35 ± 0.85 х 10 ⁶ м ³ (с учетом сыпучих материалов). В обычном состоянии умеренной постоянной активности вулкана Этна основная щелочная магма извергается при почти постоянной температуре 1080 ^о C (это соответствует примерно 40 ^ 50% кристаллической фазы), в то время как при пароксизмальных извержениях (очень сильных и бурных, когда вскрывается вся полость кратера вулкана) температура магмы превышает 1125 ^о Си может быть еще больше.

В вычислительных экспериментах задавались следующие исходные данные для математической модели: – рельеф местности, по которой будут растекаться лавовые потоки (Рис. 4) ;

– входные условия: объемная скорость экструзии лавы, ее температура, объемная доля кристаллов, местоположение и геометрия выходного отверстия, из которого извергается магма;

– взаимодействие лавы на ее свободной границе с окружающей средой;

– физические свойства лавы: плотность, теплопроводность, реология, время релаксации кристаллов.

Эксперимент 1 . Рассмотрим процесс экструзии вулканической магмы из кратера вулкана и растекания лавы по заданному рельефу местности, описываемый математической моделью (1) – (11) . Расчетная область имеет размеры Ω = (0,4000) х (0,2600) м ² . Начало координат соответствует спутниковым координатам (x ₀ = 500100 м, y 0 = 4175860 м). Рельеф H = H(x,y) задан на рисунке 6. Точное местоположение кратера вулкана определить по спутниковым снимкам невозможно. Для компьютерного моделирования координаты подобраны так, что подходят под данные наблюдения за растеканием лавы. Жерло вулкана разделено на 3 источника, из которых магма выходит на поверхность. Для каждого источника по спутниковым координатам рассчитаны радиус и магнитуда скорости: x i = 500316 м, y i = 4177709 м, r i = 15 м, v i = 0.0113 м ^ с ^{- 1} ; Х 2 = 500268 м, у 2 = 4177803 м, Г 2 = 23 м,

( а )

( б )

( в )

Температура, [К]

Глубина лавы, [м]

Фактическая вязкость лавы lg( ^ eff ) , [Па с]

Рис. 7. Растекание лавы при постоянной динамической вязкости и разной реологии: ньютоновская ( a ), бингамовская ( б ), Гершеля–Балкли ( в )

v2 = 0.00607 м-с-1; х3 = 500283 м, у3 = 4177756 м, r3 = 30 м, v3 = 0.000351 м^с-1. При этих входных данных за 48 часов наблюдения за процессом объем вытекшей лавы составляет ~1.64х 106 м3. Выходящая из кратера магма имеет температуру Tin = 1350 К и долю кристаллов ϕin = 0.4. Параметр, характеризующий долю покрытия жидкой лавы твердой коркой, равняется f = 0.17. Остальные параметры, использованные в расчетах, приведены в таблице.

Таблица. Параметры в математической модели и их значения

Параметр	Физический смысл, размерность	Значение
c	удельная теплоемкость лавы, [Дж ^ кг -М К - 1 ]	1200
g	ускорение свободного падения, [м • с - ]	9.81
k	теплопроводность лавы, [Дж - с - 1 м - 1 • К - 1 ]	2.0
L ∗	коэффициент скрытой теплоты, [Дж - кг - 1 ]	3.5 x 10 —5
T air	температура воздуха, [К]	300
T in	температура магмы, поступающей из кратера вулкана, [К]	1350
T diff	температуры на границе раздела лавы и грунта, [К]	1170
е ( Т )	эффективная излучательная способность	Ур. (8)
n ( T )	степенной индекс в описании реологии Гершеля–Балкли	Ур. (11)
Ф eq ( T )	объемная доля кристаллов в равновесном состоянии	Ур. (7)
λ air	коэффициент нелинейной конвективной теплоотдачи,	5.5
ρ	плотность лавы, [кг - м -3 ]	2500
σ	константа Стефана-Больцмана, [Дж - с - 1 - м - 2 - К - 4 ]	5.67 x 10 —8
τ	время релаксации кристаллов, [ч]	5
W	содержание водяного пара в лаве, [%]	0.1
n diff	эмпирический параметр в уравнении (5)	4
m	эмпирический параметр в уравнении (5)	12

Для аппроксимации производной по времени применялась схема Эйлера. С учетом нелинейности модели шаг по времени выбирался так, чтобы число Куранта не превосходило единицу. Для аппроксимации градиента прибегали к схеме minMod [35] , которая относится к классу TVD схем (Total Variation Diminishing) и обеспечивает выполнение принципа максимума. Расчетная сетка состояла из ^ 400000 ортогональных ячеек. Каждая ячейка имела площадь 5 х 5 м 2 . Поскольку в некоторых примерах вязкость меняется на несколько порядков, система (1) – (7) решалась на основе неявной схемы, которая предпочтительнее, хотя и требует больше ресурсов. Потери массы при этом не превосходили 3% на всем отрезке времени моделирования. СЛАУ, которые получаются при использовании неявного метода аппроксимации дифференциальных операторов в (1) – (3) , (5) , (7) , решались бинаправленным методом сопряженных градиентов [36] .

В рассматриваемом примере состояние лавы отвечает моменту времени в = 48 ч от начала извержения. В данном примере производится сравнение течений следующих жидкостей: ньютоновской m ¹ = Mn = 10 6 Па<; бингамовской M B = M N + т ₀ (Т)Ё - ¹ Па - с; с нелинейной реологией Гершеля-Балкли p H = m _n ё ^п(т ) ^{- 1} + т ₀ (Т ) е ^-1 Па<. Если М ~ M N , то лава с ньютоновской реологией при заданном расходе за 48 часов распространится на 4 км; число Рейнольдса будет близко к значению 0.25; предел текучести в моделируемом интервале температур составит 10 1 <  т ₀ <  10 5 ; индекс нелинейности будет изменяться в пределах 0.3 <  n <  0.8. На рисунке 7 представлены распределения температуры, глубина лавы и фактической вязкости для жидкостей с принятыми физическими свойствами.

Отметим, что при учете в реологии жидкости предела текучести и нелинейных эффектов формируется более узкое расчетное лавовое русло, чем в случае ньютоновской жидкости. Поэтому результаты рисунка 7б , в ближе к наблюдаемому течению, приведенному в [31] , чем течение с ньютоновской реологией (Рис. 7a ). При этом глубина лавы также не достигает наблюдаемых значений. Поэтому реология Гершеля–Балкли лучше отражает поведение лавового потока на склоне Этны. Средняя вязкость потока оценивается значением ~ 10 6 -10 7 Па - с.

Эксперимент 2. Моделирование растекания лавы производится в тех же условиях, что и в Эксперименте 1. Сравниваются также течения с разной реологией, но динамическая вязкость жидкости отличается от Эксперимента 1: у ньютоновской жидкости м = M D (T) Па ^ с, у бингамовской жидкости M B _T = M D (T) + т ₀ (Т )Ё ^{— 1} Па ^ с, у жидкости с нелинейной реологией Гершеля-Балкли M H _T = M D (T)Ф ^{п ( Т ) - 1} + t ₀ ( T ) e ^-1 Па ^ с, где M D (T ) определяется по формуле (9) ; содержание водяного пара принято постоянным и равным 0.1%. На рисунке 8 демонстрируются распределения температуры, глубина лавы и фактическая вязкость по прошествии в = 48 ч с момента начала извержения. Параметр f выбран таким, чтобы за это время при заданном расходе поток с любой реологией распространялся на 4 км.

Важно, что все течения образуют узкое русло, глубина лавы во всех трех случаях количественно укладывается в наблюдаемый интервал значений. Бингамовская жидкость течет медленнее остальных. Обнаруживается

( а )                                                  ( б )                                                  ( в )

Температура, [К]

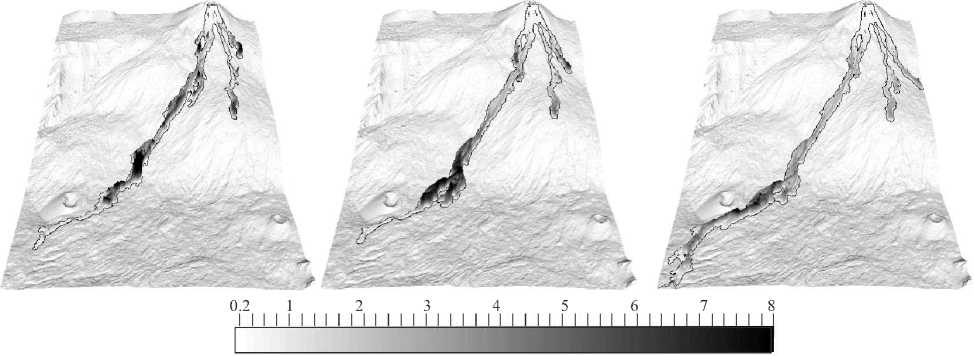
Глубина лавы, [м]

Фактическая вязкость лавы lg( ^ eff ) , [Па с]

Рис. 8. Картины растекания лавы при динамической вязкости, зависящей от температуры и различной реологии: ньютоновская, f = 0 . 4 ( a ), бингамовская, f = 0 . 17 ( б ), Гершеля-Балкли, f = 0 . 1 ( в )

формирование дамбы в нижнем течении лавы. В этом же месте охлаждение и учет скоростей сдвига в реологии выражаются в разветвлении потока лавы, и он находит себе новое русло. При реологии Гершеля–Балкли дамба не образуется.

Проведенные вычислительные эксперименты не имели цели наиболее точно отобразить реальное течение, которое создавшееся по прошествии 48 часов [31] и проведены при неопределенностях в задании исходных параметров модели. Так, например, точное расположение и геометрия выходного отверстия лавы не были доступны для прямого просмотра. Для адекватного моделирования эти координаты реконструировались путем подбора результатов численного эксперимента таким образом, чтобы они соответствовали наблюдаемой морфологии потока. Но как раз эти параметры и сказываются существенно на результатах компьютерного моделирования. Другим важным фактором является динамика образования лавовой корки, которая влияет на тепловой баланс внутри лавы. Для реконструкции данного параметра необходимо иметь гораздо больший объем данных полевых измерений.

Время счета задачи определяется ее размерностью, количеством занятых вычислениями ядер и фактической вязкостью лавы, заложенной в модель. Изменение вязкости происходит от 10 ² до 10 ¹² Па · с, что заставляет проводить расчеты с малым шагом по времени для того, чтобы число Куранта обеспечило устойчивость в расчетах, и использовать неявные методы интегрирования дифференциальных уравнений.

• 7.    Заключение

  В работе к моделированию распространения лавового потока по наклонному рельефу местности представлен подход, в котором численно решаются входящие в математическую модель усредненные по глубине потока уравнения переноса массы, импульса и энергии. Подход базируется на физически обоснованном описании процесса распространения лавы и является адекватным компромиссом между полным трехмерным моделированием и требованием сокращения вычислительного времени, необходимого для обработки данных в режиме реального времени. Подход реализован в пакете OpenFOAM и применен для изучения эволюции реального потока лавы, излившейся во время извержения Этны в декабре 2015 года. Хорошая вычислительная производительность делает этот подход потенциальным инструментом для прогнозирования траекторий лавовых потоков, оценки рисков стихийных бедствий. Приведены примеры моделирования потоков с различными реологическими параметрами. Сопоставление результатов численного моделирования с данными о реальных последствиях извержений показывает важность адекватного учета реологических свойств распространяющегося потока на примере модели Ньютона в сравнении с моделью Бингама и нелинейной моделью Гершеля–Балкли.

Используемый алгоритм может быть усовершенствован для лучшей обработки исходных условий в конкретных ситуациях. Более точная оценка входных параметров модели (реологии и ее описания, скорости экструзии, тепловых параметров и условий кристаллизация) является сложной проблемой, требующей также более точных полевых измерений во время извержений. При этом с помощью предлагаемой модели можно оценивать параметры, которые не могут быть измерены в раскаленной лаве. Численные методы вычислительной гидродинамики дают возможность дополнять лабораторные эксперименты благодаря созданию виртуальных тестовых примеров для имитационных экспериментов по изучению влияния реологических свойств жидкости на продвижение потока и его эволюцию с течением времени, для проверки модели вязкости и сравнения результатов расчетов с полевыми измерениями с целью установления аналитических законов, которые приведут к их наилучшему соответствию.

Расчеты выполнены на суперкомпьютере «Уран» в ИММ УрО РАН, г. Екатеринбург.