Численное моделирование электроконвекции слабопроводящей жидкости в переменном электрическом поле

Переменные воздействия (вибрационные, тепловые, электромагнитные) могут существенно изменить пороги конвективной неустойчивости, повлиять на свойства нелинейных течений [1–4], обеспечить эффективный способ управления массо- и теплопереносом в различных технологических ситуациях. Чаще всего рассматривается так называемый высокочастотный предел, когда период внешнего воздействия меньше характерных времен системы, вследствие чего может быть применен метод осреднения [5–8]. Зависимые от амплитуды и частоты переменные электрические поля представляют собой важный и удобный способ воздействия на свойства течений. Так, варьируя амплитуду и частоту внешнего поля, можно не только изменить характер течения, но и вызвать в системе колебания хаотического характера [3, 4]. Исследование электроконвекции представляет, кроме того, еще и практический интерес в связи с применением её в промышленности, например, в электрогидродинамических насосах.

В изучении электроконвекции слабопроводящих жидкостей, несмотря на большое количество публикаций по исследуемой тематике, присутствует немало нерешённых проблем, связанных, прежде всего, с наличием множества механизмов возникновения свободных зарядов в жидкости [9, 10]. Основными такими механизмами являются инжекционный, диэлектрофоретический

и электрокондуктивный. В настоящей работе обсуждается только электрокондуктивный механизм [9, 11], в котором зарядообразование связано с зависимостью электропроводности среды от температуры. Этот механизм проявляет себя в случае неоднородного нагрева жидкостей (трансформаторного и конденсаторного масел), применяемых в электротехнике.

В рамках предположения о мгновенной релаксации заряда нелинейные электроконвективные режимы течений слабопроводящей жидкости исследованы для случая переменного электрического поля произвольной частоты [12] и в высокочастотном пределе [13]. Отметим, что осредненная система уравнений электроконвекции в переменном поле для произвольной релаксации зарядов записана в работе [10], где подчеркивается важность учета диэлектрических потерь в высокочастотном случае. То обстоятельство, что время релаксации заряда конечно, принято во внимание при рассмотрении электроконвекции слабопроводящей жидкости только в случае постоянного электрического поля [14, 15]. В настоящей работе изучены колебательные и хаотические режимы электроконвекции в переменном электрическом поле произвольной частоты и при конечном времени релаксации заряда. Безразмерные параметры задачи (число Прандтля и электрическое число Прандтля), используемые в численном моделировании, взяты из экспериментальных работ по изучению электроконвекции в реальных слабопроводящих жидкостях [17]. Свойства рабочих жидкостей таковы, что собственные частоты колебаний системы низки, что дает право не учитывать диэлектрические потери.

2.    Постановка задачи

Рассмотрим плоский горизонтальный слой неоднородно нагретой вязкой несжимаемой слабопроводящей жидкости, находящейся в переменном вертикальном электрическом поле напряженностью E и поле силы тяжести g . Ось x совпадает с нижней границей слоя и направлена вдоль неё, ось z — перпендикулярна границам слоя. Идеально тепло- и электропроводные пластины конденсатора расположены в плоскостях z = 0, h ( h — толщина слоя) и нагреты до разной температуры: T ( 0 ) = 0 , T ( h ) = 0, где T — температура, отсчитываемая от некоторого среднего значения, а 0 — характерная разность температур. Случай 0 >  0 соответствует нагреву снизу. Потенциал поля верхней границы равняется нулю: ф ( h ) = 0, потенциал нижней границы изменяется со временем по гармоническому закону: ф (0) = U cos ( ю t ) . Здесь U — амплитуда, ю = 2 nv = 2л/ t f , где v — частота, t_f — период модуляции.

Для изучения поведения слабопроводящей жидкости в электрическом поле воспользуемся электрогидродинамическим приближением, в котором магнитные эффекты считаются пренебрежимо малыми по сравнению с электрическими [9]. В данной работе, как оговорено выше, имеет место электрокондуктивный механизм зарядообразования. Зависимость электропроводности жидкости от температуры представим как g = g ₀ ( 1 + в _а T ) , где )у — положительный температурный коэффициент электропроводности, g ₀ — электропроводность в отсутствие нагрева. Этот механизм приводит к накоплению электрического заряда, который взаимодействует с внешним электрическим полем и вызывает электрокондуктивную неустойчивость. Плотность жидкости также линейно зависит от температуры р = р ₀ ( 1 -в T ) , где в — коэффициент теплового расширения жидкости, р ₀ — плотность жидкости в отсутствие нагрева. В результате возникает термогравитационная неустойчивость.

В общем виде электрическая сила, действующая на единицу объема диэлектрической жидкости, может быть записана в виде

f = р E -1E2Ve +1 vfp—E2), e Ve 2 2 l/dp J

здесь p _e — свободный заряд единицы объема, е — диэлектрическая проницаемость жидкости. Последнее слагаемое имеет градиентный вид и приводит лишь к переопределению давления в уравнении Навье–Стокса. Поскольку в задаче рассматриваются жидкости, в которых диэлектрическая проницаемость практически не зависит от температуры, то вторая (диэлектрофоретическая) часть электрической силы, связанная с неоднородностью диэлектрической проницаемости, отсутствует. В таких жидкостях при полях порядка 1 кВ/см электропроводность зависит от температуры сильнее, чем диэлектрическая проницаемость: Р _а » Р _е [10, 16-19]. Движение в этом случае порождается только первой (кулоновской) частью силы, связанной со свободным объемным электрическим зарядом.

Предполагаем, что максимальная разность потенциалов на пластинах конденсатора не превышает критического значения U ^* , начиная с которого влияние инжекции на движение жидкости существенно.

Согласно оценкам, проведённым в [10], U ^* имеет порядок 1 кВ, что соответствует напряженностям поля примерно 1 кВ/см при межэлектродных расстояниях, больших или равных 1 см. В уравнении теплопроводности пренебрегаем вязкой диссипацией и джоулевым разогревом. Коэффициенты динамической вязкости и температуропроводности считаем постоянными. Ограничиваем исследование рамками приближения Буссинеска. Так как возникновение конвекции вызывается пространственной неоднородностью плотности и электропроводности жидкости, то, как правило, коэффициенты р , Р _ст составляют ~ 10 - 2 град^-1, поэтому в обычных (интервал температур 0 + 100 ° C) условиях при умеренном ( ~ 10 град) нагреве Р _ст 0 ^ 1. Теоретические исследования электротермической конвекции в постоянных полях, использующие это условие, находятся в хорошем согласии с экспериментом [17, 18].

Введём масштабы времени — [ t ] = p ₀ h ² /п , расстояния — [ r ] = h , скорости — [ v ] = х/ h , температуры — [ T ] = 0 , потенциала — [ ф ] = U , поля — [ E ] = U/h , давления — [ p ] = пх/ h ² , плотности заряда — [ p e ] = е U/h ² . Здесь v = ( u , v , w ) — вектор скорости, п — динамическая вязкость, х — коэффициент температуропроводности жидкости. Тогда система уравнений электроконвекции слабопроводящей жидкости в безразмерном виде с учётом равновесного решения примет вид [13]:

^+ + ”(v • V)v = -Vp + Av + RaCTpey cos tot + Ra T Y, ат ,

• -r— + ( v -V ) T = A T ,    div v = 0,

dt an   Pr ,    .         ат

• -r      + -re. ( v -V ) p +p +—— cos to t = 0.

e a t    -r^v      e          a z

Здесь Y = ( 0,0,1 ) .

Рассмотрим случай свободных недеформируемых изотермических границ слоя, на которых обращаются в нуль вертикальная компонента скорости и касательная компонента тензора вязких напряжений (штрихом обозначена производная по z ):

z = 0: w = w" = 0, T = 1, ф = cos (to t), z = 1: w = w" = 0 , T = 0, ф = 0.

Система (1) содержит следующие безразмерные параметры: тепловое число Рэлея Ra , число Прандтля

-r, электрическое число Прандтля -r e и малый параметр S _CT , характеризующий неоднородность электропроводности жидкости:

Ra = E0Se0h3, -r = JL, -r '  , пх             Xp0          h Р0СТ0

S = р 0 , Ra = JUS. СТ СТ , ст пх

.

Здесь Ra _CT — электрический аналог числа Рэлея, меняющий знак при изменении направления градиента температуры. Электрическое число Прандтля характеризует отношение времени релаксации заряда и гидродинамического времени (времени распространения гидродинамических возмущений) в слое. Возьмём это отношение равным 30, как и в эксперименте на реальных слабопроводящих жидкостях [17]. Малость параметра S _CT « 1 дает возможность использовать безындукционное приближение, в котором в расчет берется только внешнее электрическое поле (по сравнению с ним электрическое поле, связанное с перераспределением заряда в жидкости, пренебрежимо мало) [9]. Несмотря на малость S _CT , значение электрического аналога числа Рэлея Ra _ст остается конечным.

Представим поля скорости, температуры, давления и плотности заряда в виде: v, T = T0 +9', Р = Ро + P', Pe0 =Pe0 + Pe (штрихи означают отклонения величин от равновесных значений T0, p0, pe0, далее штрихи опускаем). Плоские и пространственные возмущения одинаково опасны, но, поскольку задача изотропна в плоскости слоя, ограничимся рассмотрением только плоских возмущений: v = (и,0, w), д/ду = 0 . Введем функцию тока ф и представим компоненты вектора скорости как дш      дф w = —, и =--.

д x         д z

В терминах функции тока уравнения для возмущений примут вид:

д .      1 (дш д , дш д . ] „ др,         _п д9 ,₂

—Аш + 1--Аш---Аш 1 = Ra„—-cosюt + Ra — + А ш, дt     Pr ( дx дz      дz дx   J       дx д9 дш д9 дш д9 , _ дш

Pr — + —---—— = А9 + —, д t дx дz дz дxд

„ др   Pr (дш др   дш др)д9

Pr ——e + —-1 — -— —   1 + р, +—cos ю t = 0, д t   Pr ( дx дz   дz дx )       дz с соответствующими граничными условиями:

z = 0,1: ш = ш" = 9 = 0.

Для решения системы уравнений (3) с граничными условиями (4) будем использовать метод Галеркина, применяя следующие, удовлетворяющие граничным условиям, аппроксимации полей функции тока, температуры и плотности заряда р e :

ш = ( A 1 ( t ) sin п z + A 2 ( t ) sin 2 п z ) sin п kx ,

9 = ( B 1 ( t ) sin п z + B ₂ ( t ) sin 2 п z ) cos п kx + C ( t ) sin 2 п z ,                           (5)

р e = ( D 1 ( t )cos п z + D ₂( t )cos2 п z ) cos п kx + E ( t )cos2 п z .

Здесь k — волновое число, характеризующее периодичность возмущений в плоскости слоя; A ₁ , A ₂ , B ₁ , B ₂ , D ₁ , D ₂ , E , C — амплитуды, характеризующие различные пространственные моды. В разложениях (5) присутствуют слагаемые с разной четностью по z . Это связано с тем, что в уравнение для эволюции возмущений заряда входит содержащее первую производную по z слагаемое, которое обуславливает перераспределение энергии между модами различной четности.

Коэффициенты разложения в рядах Фурье (5) (амплитуды) определяются из интегральных условий, выражающих ортогональность невязки к каждой базисной функции. Подставим разложения (5) в систему (3), проведём процедуру ортогонализации и перемасштабируем переменные

Pr          ,    V2(1 + k ²1        ,    V2(1 + k ²)_ТЛ „    72_ТЛ

^ —;-----t-t,   A. ^---------XX,   A2 ^--------Vy ,   B, ^

п2(1 + k2)        1 k                2 k

B2 ^ — W , C ^ —,  D1 ^ 2SS ,  D2 ^ 2л12Т,  E ^ U, пп в результате получим восьмимодовую модель электроконвекции (точка над переменными обозначает производную по времени):

.S =- g S + XU - g Y cos ю t ,    T =- g T - g W cos to t ,

U = - g U - XS - 2g Z cos ю t ,    V = Pr ( - d V + ( r W + e S cos ю t )/d ) ,

W = - d W + V ,    v X = Pr ( - X + r Y - e T cos ю t ) ,

Y = - Y + X + XZ ,    Z =- b Z - XY .

Здесь введены следующие новые параметры:

Ra       Ra r=      , e= σ ,

Ra 0         Ra σ0

Ra 0

п ⁴ ( 1 + k ² ) 3

k ²

_ 3 п ⁴ (1 + k ² ) ³

^Ra -0 = ”"8e

4          4 + k ²       _ Pr

1+k2 ’   d = T+kT ’   g =п2(1 + k2)Pre , где r , e — нормированные тепловое и электрическое числа Рэлея; Ra0 , Raσ0 — критические числа, при которых начинается термогравитационная или электрокондуктивная конвекция соответственно;

b , d — геометрические параметры, зависящие от волнового числа; g — параметр, определяющий отношение времени релаксации тепловых возмущений и возмущений заряда. Заметим, что электрическое число Рэлея может быть как положительным, так и отрицательным в силу того, что по определению (2) линейно зависит от разности температур между обкладками конденсатора и при нагреве сверху будет отрицательным.

Динамическая система (6) является обобщением маломодовой модели Лоренца [20] на случай электроконвекции слабопроводящей жидкости с электрокондуктивным механизмом зарядообразования в переменном электрическом поле. Фактически для получения системы (6) использован метод Бубнова–Галеркина с небольшим числом базисных функций. Несмотря на это ограничение, применение подобного подхода для описания конвекции в переменных полях [21, 22] показывает неплохое согласие теоретических и экспериментальных данных вплоть до значений управляющего параметра, соответствующих состоянию надкритичности 2,5 [21].

Электроконвекция на основе маломодовых моделей изучалась в постоянном [15] и высокочастотном [13] полях. Важно отметить, что в высокочастотном пределе, где амплитуда и частота электрического поля объединены в один параметр, а резонансные явления исключены, вместо системы уравнений (6) в [13] анализируется система уравнений, полученная из (6) методом осреднения в случае мгновенной релаксации заряда.

Интегрирование системы уравнений (6) проводилось с помощью метода Рунге–Кутты–Мерсона 4-го порядка. Спектральный состав отклика электроконвективной системы находился с помощью быстрого преобразования Фурье. Подчеркнем, что характерные частоты системы находятся в пределах v ~ 0,1 и требуют больших расчетных интервалов времени. В частности, при вычислении константы Фейгенбаума (постоянной, характеризующей бесконечный каскад бифуркаций удвоения периода при переходе к хаосу) использовались временные интервалы до 50 000 безразмерных единиц, что отвечает 10 000 периодов колебаний внешнего поля. Такой большой временной интервал вызван необходимостью уменьшения влияния шума при определении амплитуд в спектрах преобразования Фурье.

3.    Пороги устойчивости и нелинейная динамика течения в слое

Проведено исследование эволюции течений для параметров Pr = 400 , Pr e = 30, свойственных таким слабопроводящим жидкостям как конденсаторные и трансформаторные масла [16], кукурузное масло Mazola [18], при интенсивности нагрева r = 0,8. Значение волнового числа соответствовало минимуму нейтральной кривой электроконвекции в отсутствие гравитации (r = 0) и равнялось к = 0,933 , значения других параметров были такими: b = 2,13 8, d = 2,604, g = 0,722 [14, 15].

На рисунке 1 представлена карта устойчивости режимов электроконвекции на плоскости «электрическое число e — период колебаний поля 1jv». Ниже кривой наблюдается равновесие, все возмущения затухают, и тепло передается теплопроводным механизмом, а число Нуссельта (среднее по времени значение безразмерного теплопотока, приходящегося на единицу горизонтальной границы конденсатора) равняется единице (Nu = 1). Выше кривой мягко возникают электроконвективные регулярные колебания, в спектре Фурье которых

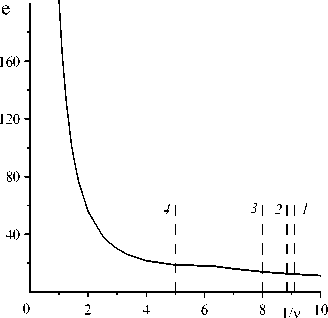
Рис. 1. Карта устойчивости на плоскости электрическое число e - период колебаний поля 1/ v ; штриховые линии соответствуют значениям частоты v : 0,11 (линия 1 ); 0,113 ( 2 ); 0,125( 3 ); 0,2( 4 )

существуют кратные частоты v _m = m v , где m — целое число. При значении (У v ) < 6,1 основная частота в спектре равняется удвоенной внешней частоте v main = 2 v , а при (V v ) >  6,1 совпадает с ней: v m_am =v . Таким образом, в системе возможны два разных типа колебаний синхронного отклика, что аналогично параметрическому возбуждению диэлектрофоретической конвекции [3].

Рассмотрим подробно поведение системы при частоте внешнего электрического поля v = 0,11 (сечение 1 на рисунке 1). Отметим, что эта частота является собственной частотой колебаний жидкости в постоянном электрическом поле. При потере устойчивости реализуется синхронный режим с частотой колебаний vmain =v, а Фурье-спектр временной эволюции сигнала содержит только нечетные гармоники внешней частоты. Рост амплитуды поля приводит к изменению типа колебательного режима и характера теплопереноса через конвективную ячейку. На рисунке 2а представлен график зависимости теплопотока от электрического числа для частоты v = 0,11. С увеличением электрического числа, начиная со значения e = 21,9, основной частотой в системе становится удвоенная внешняя частота vmain = 2 v, причем в спектральном составе отклика системы присутствуют только ее четные комбинации. При e = 24,7 вновь появляются нечетные гармоники. Дальнейший рост амплитуды поля вызывает каскад удвоений периода колебаний, и система выходит на хаотический режим движения. Обнаружено, что хаос начинается при e = 25,87 (Рис. 2а, точка А).

С помощью метода продолжения по параметру удалось обнаружить, что при уменьшении электрического числа e имеет место явление гистерезиса (Рис. 2 а , штриховая линия). В первом справа гистерезисном переходе наблюдается каскад изменений периода. Наименьшее значение электрического параметра, при котором реализуется хаотический колебательный режим, это e = 26,51 (Рис. 2 а , точка B). Окончательный период характеризуется удвоенной внешней частотой v main = 2 v . Оставшиеся две гистерезисные петли представляют собой переходы между колебательными режимами.

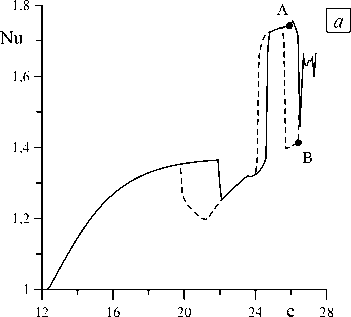
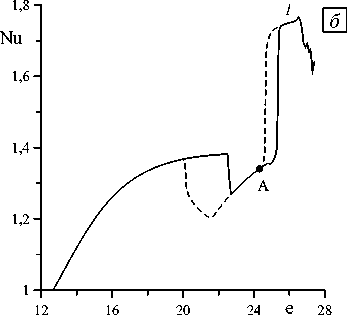
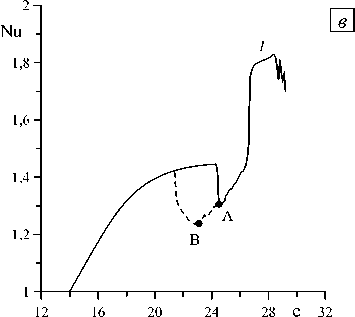
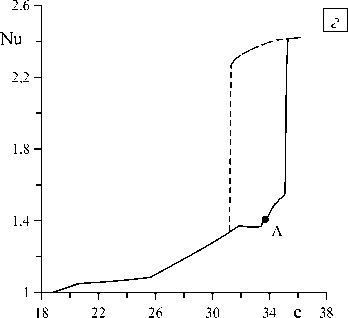
Рис. 2. График зависимости безразмерного теплопотока Nu от электрического числа e при различных значениях внешней частоты v : 0,11 ( а ); 0,113 ( б ); 0,125 ( в ); 0,2 ( г )

Под воздействием внешнего электрического поля с частотой v = 0,113, как и в предыдущем случае, в системе сначала возникает режим колебаний с частотой v main = v и Фурье-спектром, содержащим одни нечетные гармоники (Рис. 2 б ), соответствующий движению по штриховой линии 2 на рисунке 1. С увеличением электрического поля изменяется тип периодических колебаний. Со значением e = 22,5 соотносится спектральный состав отклика системы, содержащий в качестве главной гармоники удвоенную внешнюю частоту v main = 2 v , а также её четные и нечетные комбинации. Дальнейшее увеличение частоты поля сопровождается каскадом бифуркаций удвоения периода, и при e = 24,28 появляется хаос (Рис. 2 б , точка А). При углублении в область хаоса наблюдается окно периодичности с колебаниями, характеризуемыми удвоенной внешней частотой v main = 2 v (Рис. 2 б , область 1 ).

При движении в пространстве параметров справа налево обнаружены две гистерезисные петли (Рис. 2 б , штриховая линия). Первая справа петля является продолжением окна периодичности в область хаоса, вторая представляет собой переход между различными типами периодических колебаний. Следует отметить, что в рассматриваемой области параметров минимальное значение числа e, при котором реализуются хаотические режимы, находится за пределами области гистерезиса (Рис. 2 б , точка А).

Для внешней частоты v = 0,125 (штриховая линия 3 на рисунке 1), как и для двух предыдущих значений, возникновение неустойчивости сопровождается колебаниями по-прежнему с главной гармоникой v main = v и ее нечетными комбинациями в спектре Фурье, но теперь с дальнейшим ростом поля, вплоть до наступления хаоса, реализуется только этот режим (Рис. 2 в ).

Уменьшение безразмерного параметра e также сопровождается явлением гистерезиса (Рис. 2 в , штриховая линия). Наименьшее значение e = 23,13, при котором наблюдаются хаотические режимы, лежит именно на гистерезисной ветви (Рис. 2 в , точка B). Переход от хаоса к периодическим колебаниям осуществляется через каскад изменений периода. Для окончательного периода характерна удвоенная внешняя частота v main = 2 v . Наступление хаоса на верхней ветке (e = 24,30), соответствующей увеличению параметра e, связано с тем, что система резко переходит в состояние, отвечающее нижней ветви, где уже реализуются хаотические колебания (Рис. 2 в , точка А). При увеличении амплитуды колебаний поля в области хаоса можно увидеть окно периодичности с удвоенной внешней частотой колебаний v - = 2 v (Рис. 2 в , область 1). main

Отметим, что при качественном сравнении фрагментов ( а ), ( б ) и ( в ) рисунка 2 видно, что изображенные на них зависимости ведут себя похожим образом, но при различных внешних частотах точка появления хаоса лежит на разных участках кривых. Так, для внешней частоты электрического поля v = 0,11 хаос впервые обнаруживает себя на самом высоком участке кривой (Рис. 2 а , точка А). Частоте v= 0,113 отвечает точка А на рисунке 2 б , то есть точка «сползла» вниз по кривой. С ростом частоты ( v= 0,125) хаос «опускается» еще ниже и переходит на гистерезисную ветвь (Рис. 2 в , точка В).

В отличие от этих случаев, при внешнем поле v = 0,2 (сечение 4 , Рис. 1) потеря устойчивости происходит колебательным образом с частотой v main = 2 v , а Фурье-спектр колебаний представляет собой набор ее четных комбинаций. Значению e = 20,6 соответствует спектральный состав из нечетных гармоник, а начиная с e = 21,1, основной частотой служит частота v main =v . Увеличение амплитуды поля не влечет изменение частоты колебаний слоя, но начиная со значения e = 25,7, спектр Фурье содержит только её нечетные комбинации. Дальнейший рост амплитуды поля вновь вызывает переход на другой колебательный режим. Как только электрическое число принимает значение e = 31,9, в спектре опять появляются четные гармоники. С последующим увеличением поля рождается субгармонический каскад и наступает хаос (Рис. 2 г ).

Для частоты v = 0,2 проведена оценка величины константы Фейгенбаума. Её точное значение определяется соотношением [23]:

5 = lim e k e k ^{- 1} = 4,669.... ^k " ^ek + 1 ^{- e}k

Для ее вычисления необходимо знать три точки бифуркации удвоения периода. В работе использовались третья, четвертая и пятая бифуркации, что уже позволило оценить константу с достаточно малой погрешностью. Первая бифуркация удвоения периода связана с e = 33,453: появляется частота, равная половине внешней ( v = 0,1). Второму удвоению отвечает e = 33,572 ( v = 0,05 ), третьему — e = 33,6810 ( v = 0,025 ), четвертому — e = 33,6972 ( v = 0,0125), пятому — e = 33,7007 ( v = 0,00625). Хаотические режимы впервые возникают при e = 33,71 (Рис. 2 г , точка А). На рисунке 3 представлены Фурье-спектры временной эволюции сигнала системы после пятой бифуркации и при хаотическом режиме. Значения e ₃ , e ₄ , e ₅ , соответствующие последним трём точкам бифуркаций, уточнялись до четвертого знака после запятой в целях уменьшения погрешности оценки числа Фейгенбаума. При их использовании вычисленное значение константы составило 5 = 4,629 , что отличается от ее точного значения на 0,9%.

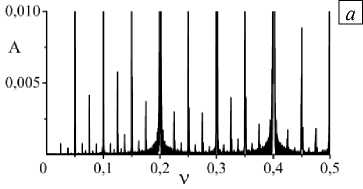
Рис. 3. Спектры Фурье отклика системы при v = 0,2 : после пятой бифуркации (e = 33,7016) ( а ); при хаотическом режиме (e = 33,9000 ) ( б )

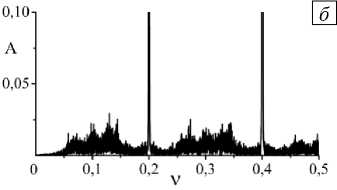
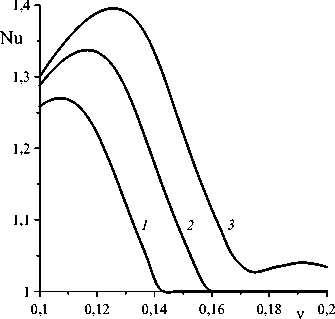
Рис. 4. График зависимости безразмерного теплопотока Nu от частоты внешнего поля v ; электрическое число e имеет значения: 16 (линия 1 ); 18 ( 2 ); 20 ( 3 )

Использование метода продолжения по параметру позволило выявить гистерезисную петлю, представляющую собой переход между колебательными режимами. Отметим, что в рассматриваемой области на гистерезисной ветви хаотических режимов не обнаружено.

Приведем также зависимости числа Нуссельта, характеризующего теплопоток через конвективную ячейку, от частоты при различных значениях электрического числа Рэлея (Рис. 4). Из рисунка видно, что имеет место резонансное усиление теплопотока (числа Нуссельта), что связано с повышением интенсивности электроконвективных течений при совпадении частоты внешнего поля с собственной частотой конвективной ячейки. Сдвиг максимума числа Нуссельта в область высоких частот электрического числа Рэлея связан с ростом собственной частоты при увеличении напряженности электрического поля [12].

4.    Заключение

В работе изучена электроконвекция слабопроводящей жидкости, находящейся в переменном электрическом поле горизонтального конденсатора. Основную роль в образовании зарядов играет электрокондуктивный механизм. На основе восьмимодовой модели электроконвекции проведен анализ поведения жидкости. Построена карта устойчивости на плоскости «электрическое число – период колебаний поля». Подробно рассмотрено поведение системы при четырех частотах внешнего электрического поля и показано, что в случае, когда эффективное электрическое число Рэлея превышает порог устойчивости, мягко возбуждаются колебательные режимы, и в результате эволюции система выходит на периодические вторичные течения. Рост степени надкритичности ведет к переходу в хаотический режим. При обсуждаемых частотах переход к хаосу осуществляется через каскад бифуркаций удвоения периода. Для частоты внешнего электрического поля v = 0,2 по значениям электрического числа e _n , соответствующим третьей, четвертой и пятой бифуркациям, проведена оценка константы Фейгенбаума. Отличие её от точного значения константы составило 0,9%.

Авторы благодарят рецензентов за полезные советы, которые помогли улучшить текст статьи.

Работа выполнена при финансовой поддержке РФФИ (проекты № 13-01-00171-а, 14-01-31253-мол_а).