Численное моделирование эволюции бактериальной популяции в легких человека

В процессе жизнедеятельности человек постоянно взаимодействует с окружающей средой, получая из нее необходимые вещества и подвергаясь неблагоприятному воздействию. Влияние негативных факторов окружающей среды на протяжении жизни человека приводит к ухудшению его здоровья, одной из причин является инфицирование бактериальной флорой.

В настоящее время существуют различные клинико-лабораторные и функциональные методы наблюдения за организмом человека, которые дают комплексное представление о текущем состоянии здоровья пациента. Однако полученные данными методами результаты отражают состояние пациента лишь на момент измерения и не позволяют осуществлять прогнозирование [1, 2]. В основе этих мето- дов лежат анализы пациента, результаты которых сопоставляются с интервалами нормы, на основании чего делаются выводы о состоянии здоровья. Кроме того, многие из методов исследования являются весьма дорогостоящими и трудоемкими.

Качественно отличным подходом для более глубокого изучения и прогнозирования процессов, протекающих в органах человека, представляется математическое моделирование. Многие труднореализуемые натурные исследования могут быть заменены вычислительными экспериментами с использованием математических моделей. Методы математического моделирования позволяют экономить ресурсы и время, изменять начальные условия, анализировать развитие болезни по различным сцена-

Пиль Никита Евгеньевич – студент (e-mail: ; тел.: 8 (919) 467-49-69; ORCID: .

Чигвинцев Владимир Михайлович – кандидат физико-математических наук, научный сотрудник отдела математического моделирования систем и процессов (e-mail: ; тел.: 8 (342) 237-18-04; ORCID: .

риям, что говорит об универсальности подхода: можно использовать одну математическую модель для разных случаев заболевания.

Создание модели эволюции бактериальной популяции в легких человека является частью более общей задачи – создания математической модели для описания человеческого организма как связной совокупности органов и систем, в которой предлагается для каждого органа ввести некоторую меру функционального повреждения, показывающую, насколько нарушена его функция [3]. Диапазон изменения поврежденности – от 0 до 1 (0 – отсутствие функциональных нарушений, 1 – полное невыполнение функций). Данная модель включает подмодели пищеварительной, иммунной и эндокринной и дыхательной систем [4–6].

Динамику роста и пространственное распределение патогенных микроорганизмов можно описать при помощи популяционных моделей. С точки зрения описания базовых принципов значительный интерес представляет модель Моно [7], в которой численность популяции зависит от наличия питательной среды, и модель Лотки – Вольтерра [8], описывающая конкуренцию популяций. Для описания распределения популяции в пространстве в ряде работ [9–12] используются клеточные автоматы. Моделируемая область дискретизируется, определенным ячейкам присваиваются значения численности популяции и задаются правила перемещения популяции. Недостаток данных моделей заключается в сложности перехода от двумерных задач к трехмерным, а также трудностях биофизической интерпретации правил, по которым работают клеточные автоматы. Среди моделей с непрерывным временем интересными представляются работы [13, 14], в которых рассматриваются процессы эволюции бактериальных популяций, используемых в нефтедобывающей отрасли. Движение бактериальной популяции обусловливается градиентом давления и наличием диффузии. Модель описывается системой дифференциальных уравнений в частных производных.

Основные принципы построения иммунологических моделей описаны в работе [15], в которой рассматривается динамика популяции патогенных микроорганизмов и компонентов иммунной системы. Взаимосвязи между элементами модели строятся по типу «хищник – жертва» и описываются системой нелинейных дифференциальных уравнений с запаздывающим аргументом. Запаздывание вводится для описания пространственных эффектов, которые явным образом в модели не учитываются. В работах [16–18] более подробно описываются механизмы иммунного ответа, однако не учитывается пространственное распределение популяции патогенных микроорганизмов и клеток иммунной системы.

Описание динамики иммунных процессов в легких человека требует учета поведения среды. Существуют различные модели, описывающие легкие человека и дыхательные процессы. В работе [19]

рассматривается реальная геометрия дыхательных путей, однако описание процессов при данном подходе требует больших вычислительных ресурсов. Перспективным направлением к моделированию нижних дыхательных путей представляется использование модели пористой среды и теории фильтрации [6, 20, 21].

Таким образом, многие иммунологические модели не описывают явным образом пространственное распределение исследуемых характеристик в конкретном органе человека. Представляется возможным использовать подходы и методы механики течения многокомпонентных смесей в пористых средах с учетом влияния иммунологических процессов.

Цель работы – построение математической модели эволюции бактериальной популяции в легких человека с учетом динамики иммунных процессов для задачи оценки функционального повреждения легких.

Материалы и методы. Инфекционные заболевания подразумевают проникновение и / или активацию в организме человека патогенных микроорганизмов. В работе рассматривается процесс эволюции бактериальной популяции локализованной в нижних дыхательных путях. Основными характеристиками, описывающими популяцию, являются скорость деления, параметры, определяющие количество питательной среды (субстрата), способность бактерий самостоятельно перемещаться в среде и вырабатывать токсические вещества.

Известно, что организму энергетически выгоднее поддерживать на постоянном уровне концентрацию патологического антигена, нежели выводить его из организма полностью [15]. Рост численности бактериальной популяции начинается в случае ослабления иммунной системы ввиду предшествующего заболевания или проникновения патогенных микроорганизмов из окружающей среды. Одновременно с этим активизируется механизм иммунного ответа. В результате образуются воспаления в местах концентрации бактериальной популяции. Выделения, связанные с реакцией иммунной системы, вызывают уменьшение пропускной способности легких, что снижает поступление кислорода и увеличивает частоту дыхания. Бактерии в ходе своей жизнедеятельности выделяют токсины, которые негативно влияют на клетки альвеол – ухудшают барьерную и транспортную функции.

Описанные процессы протекают в нижних дыхательных путях и легких человека. Легкие представляют собой совокупность воздухоносных каналов, оканчивающихся альвеолами (рис. 1) [22].

В легких взрослого человека содержится около 600–700 млн альвеол, что создает сложности при прямом моделировании всей иерархии дыхательных путей. При этом математическое описание процессов, протекающих в легких, требует больших вычислительных ресурсов. Одним из возможных вариантов преодоления указанных вычислительных сложностей представляется использование модели пористой среды. Легкие рассматриваются в качестве сплошной насыщенной упруго-деформируемой пористой среды. Деформация возникает из-за сокращения мышц диафрагмы или поднятия ребер, в результате чего объем легких уменьшается, давление увеличивается и происходит выдох. При вдохе, реализуемом при увеличении объема, давление в легких становится ниже атмосферного, поэтому воздух попадает в организм человека. Подробно данный подход описан в работе [6].

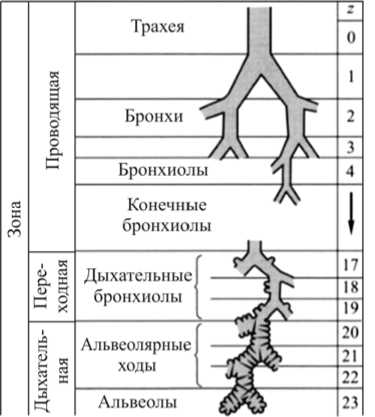
Рис. 1. Дихотомическое деление нижних воздухоносных путей согласно морфометрической модели Вейбеля [22]

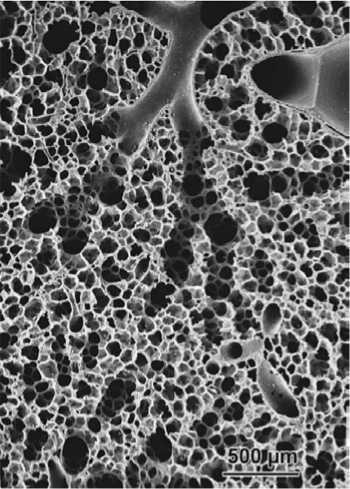
Рис. 2. Увеличенный фрагмент альвеол [23]

Модель пористой среды позволяет заменить детальную структуру альвеол и альвеолярных каналов (рис. 2) параметрами пористости и проницаемости. Пористость – это безразмерная величина, ха- рактеризующая долю пор в среде, и равная отношению объема пор к общему объему среды, состоящей из пор и деформируемых упругих перемычек. Проницаемостью называют свойство среды пропускать сквозь себя жидкости и газы.

Поврежденность легких изменяется из-за образования инфильтрата в ходе иммунного ответа и влияния токсических веществ, выделяемых бактериями, на клетки альвеол. С точки зрения модели пористой среды в ходе иммунного ответа пористость и проницаемость будут уменьшаться из-за закупорки альвеолярного пространства.

Рассмотрим математическую постановку задачи, для этого запишем уравнение баланса массы:

—+ V-(p v ) = -V- j + S , d t       ( )

где p - плотность смеси, v - вектор скорости, V -оператор Гамильтона, j – вектор диффузионного потока. Переходя к концентрациям и полагая, что смесь несжимаема, получим dCi

-v'Ji’ j = -DVC,

a a где =--+ v - V - полная производная, D - коэф- at a t фициент диффузии.

Таким образом, учитывая пористость m , за пишем уравнение массопереноса в пористой среде:

д (mCA               ,       .

(_d t ⁷ + mv -V C = V- ( mD V C ) + S ,     (3)

В первом приближении будем считать, что движения рассматриваемых компонентов обусловлены диффузией за счет градиентов концентрации. Тогда общее уравнение переноса имеет вид:

^d( mC ) =V- ( mD V C i ) + S i ,        (4)

где С_i – концентрации бактериальной популяции ( i = 1), субстрата ( i = 2), макрофагов ( i = 3), плазматических клеток ( i = 4), антител ( i = 5) и токсинов ( i = 6) соответственно; S_i – массовый источник i -й компоненты смеси.

Численность бактериальной популяции увеличивается за счет деления и потребления субстрата, уменьшается из-за естественного лизиса, действия макрофагов и антител:

S 1 = Ц -2- C 1 - k 2 C 1² - Y 13 C 3 C 1 - Y 15 C 5 C 1 . (5) k + C

Концентрация субстрата уменьшается за счет потребления бактериальной популяций и восстанавливается в результате процессов регенерации:

S 2 =- k 3 Ц       C +Y 2 f 1

k1 + C2

Изменение концентраций компонентов иммунной системы (макрофагов, плазматических клеток и антител):

S3 =Y31^C3

S4 =Y4^[p4 C3C4 - C3C4 H ( C4 - C4,0 ),(7)

S 5 =p ₅ ^ C 4 -П ₅ Y 51 c 5 C 1 -« 5 C 5 .

Концентрация токсических веществ пропорциональна концентрации бактериальной популяции и уменьшается за счет естественной нейтрализации:

S 6 =y ₆ c i -a ₆ C 6 .

Уравнения (4)–(8) с начальными и граничными условиями образуют систему уравнений в частных производных, описывающую эволюцию бактериальной популяции в пористой среде.

Функции ^ = ^ ( h ) описывают влияние повре-жденности h на функционирование иммунной системы. Поврежденность увеличивается за счет действия токсических веществ и закупорки альвеол и может уменьшаться за счет самовосстановления:

dh

— = aC₆ + aC - а_кh . dt

С учетом (9) система (4)–(8) представляет собой полную математическую постановку задачи, включающую соотношения для описания изменения концентрации за счет диффузионных процессов, соотношения для массовых источников, возникающих в результате действия иммунного ответа.

Результаты и их обсуждение. Для оценки качества построенной модели проводятся численные эксперименты, которые позволяют получить пространственно-временное распределение концентраций бактериальной популяции и компонентов иммунной системы.

В начальный момент времени полагалось известным распределение и концентрация бактериальной популяции. Учитывалась локализация бактериальной популяции, начальное распределение показано на рис. 3. Рассматривается распространение концентрации бактериальной популяции в объеме пористой среды. Рассмотренный сценарий описывает гибель бактериальной популяции.

Концентрации компонентов иммунной системы распределены равномерно внутри моделируемой области. Распределение концентрации токсинов в начальный момент времени совпадает с распределением бактериальной популяции.

На рис. 4 показано пространственное распределение концентрации бактериальной популяции в ходе иммунного ответа. С течением времени бактериальная популяция распространяется в объеме, увеличивая свою численность. Затем включается механизм иммунного ответа и в момент времени (time = 9 day) можно видеть уменьшение численности популяции, обусловленное действиями макрофагов и антител.

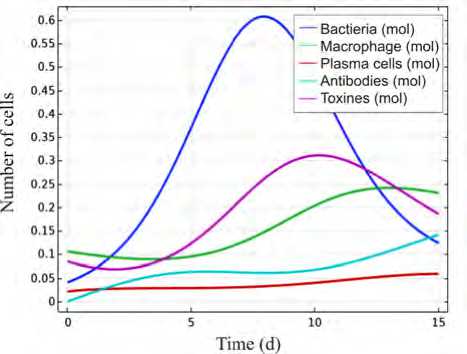
На рис. 5, а , представлены интегральные кривые численности популяций клеток иммунной системы и бактериальной популяции. Из полученных результатов видно, что бактериальная популяция начинает интенсивный рост, что приводит к генерации и росту численности популяций клеток иммунного ответа, происходит нейтрализация патогенных микроорганизмов, и численность бактериальной популяции начинает уменьшаться.

В работе рассмотрен также сценарий выживания бактериальной популяции, что может привести к гибели органа ввиду невозможности выполнять основные функции. При этом сценарии численность бактериальной популяции начинает бесконтрольно увеличиваться, что говорит о неспособности иммунного ответа нейтрализовать патогенную флору. Интегральные кривые численности компонентов иммунной системы и бактериальной популяции представлены на рис. 5, б .

Рассмотренные сценарии отличались параметрами, характеризующими состояние иммунной системы, и параметрами, описывающими бактериальную популяцию. Текущие результаты показывают качественную картину течения иммунных процессов при бактериальном заболевании в легких человека. Стоит отметить, что разрабатываемые модели во многом индивидуальны и зависят от особенностей конкретного организма: возраста, текущего состояния иммунной системы, генетики, перенесенных заболеваний.

Полученные результаты качественно согласуются с описанными в работах [14, 18].

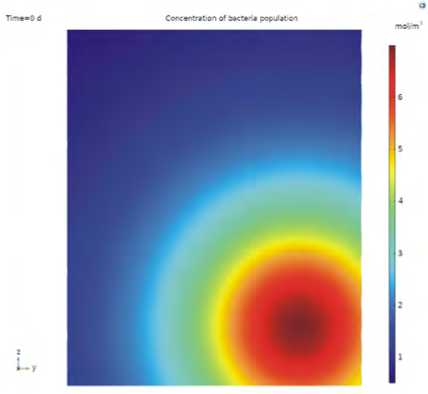
Рис. 3. Начальное распределение концентрации бактериальной популяции

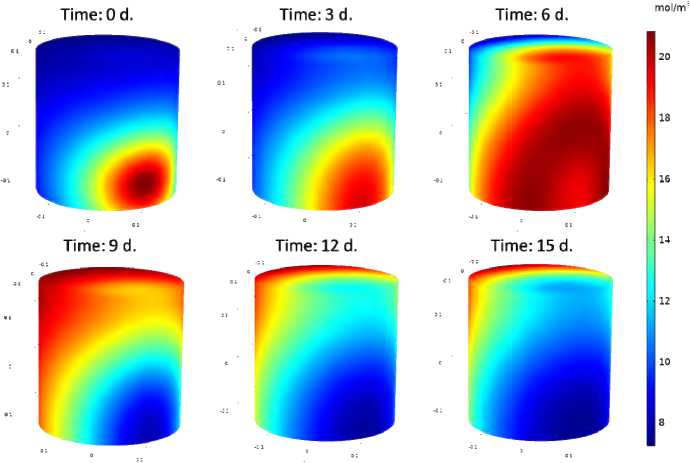
Рис. 4. Распределение концентрации бактериальной популяции в пористой среде

а

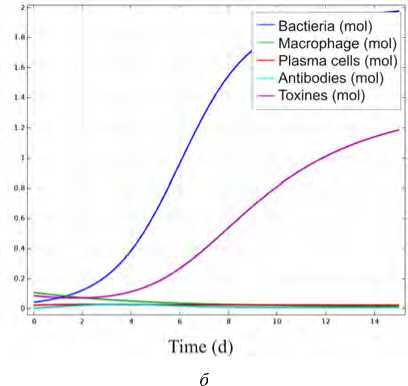
Рис. 5. Интегральные оценки концентраций компонентов иммунной системы и бактериальной популяции в рассматриваемом объеме пористой среды: а – гибель бактериальной популяции; б – выживание бактериальной популяции

Выводы. В работе рассмотрена модель для описания эволюции бактериальной популяции в легких человека. Представлены концептуальная и математическая постановки. Получены результаты численных экспериментов, описывающих сценарии гибели и выживания бактериальной популяции. Характер течения иммунных процессов определяется состоянием организма и особенностями бактериальной популяции.

В дальнейшем планируется учесть влияние процесса дыхания на перенос клеток бактериальной популяции, расширение набора элементов иммунного ответа. Планируется проведение численных исследований по влиянию поврежденности на функционирование иммунной системы в легких человека.

Представленные результаты можно считать вносящими определенный вклад в развитие методов математического моделирования для описания процессов иммунного ответа и физики течения многокомпонентных смесей в пористых средах. Для практического использования целесообразно расширить список компонентов иммунной системы и их взаимосвязей. Одним из перспективных направлений развития модели является идентификация параметров и исследование модели на предмет обнаружения новых закономерностей в иммунных процессах.

Финансирование. Исследование не имело спонсорской поддержки.