Численное моделирование эволюции границы каверны при пуске торпеды

Задача, исследования гидро и газодинамики пуска, торпеды довольно сложна, и до настоящего времени изучалась в основном с помощью постановки эксперимента. Благодаря бурному развитию вычислительной техники и появлению универсальных программных комплексов, построенных на. базе хорошо зарекомендовавших себя математических методах, появилась возможность изучения гидро и газодинамических процессов посредством математического моделирования.

В случае подводного пуска, торпеды с борта, носителя имеет место сложная картина, взаимосвязанных эффектов - сложная пространственная картина, обтекания носителя и стартующей торпеды, истечение газовой фазы в жидкость с образованием каверны и дальнейшая ее эволюция.

Важность более детального моделирования формы и параметров каверны заключается в необходимости определения значительных по величине нестационарных сил и моментов, действующих на. торпеду. Каверна, в данном случае играет важную роль, так как оказывает существенное влияние на. корму торпеды - давление в газовом пузыре достаточно быстро изменяется, изменяется и площадь воздействия газа. на. торпеду вследствие изменения формы каверны, а. кольцевая газовая струя истекает несимметрично, относительно горизонтальной плоскости симметрии торпеды, из-за. особенностей геометрии носителя.

Исследуемая в работе эволюция газовой каверны связана, с процессами образования, изменения формы и объема, каверны при истечении кольцевой газовой струи в жидкость при пуске торпеды с носителя. При этом существенные особенности вносят геометрия носителя и его движение в воде, форма, кольцевого зазора, а. также массовый расход газа, истекающего из кольцевого зазора. На рис. 1 представлена, схема, пуска, торпеды.

В.Г. Дегтярь, В.И. Пегов, Е.С. Меркулов

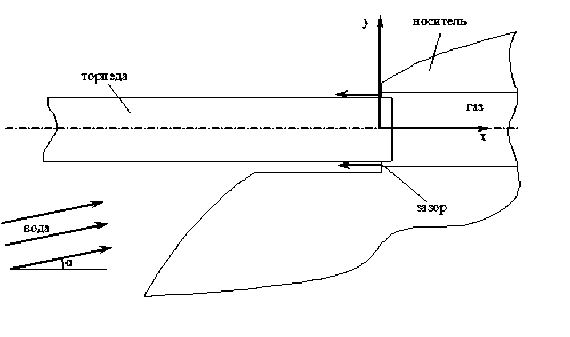
Рис. 1. Схема пуска торпеды

В момент старта носитель движется с постоянной скоростью под водой на заданной глубине с углом атаки к набегающему потоку а = 2 °. Для исследования факторов, влияющих на форму каверны и ее эволюцию данная задача решалась в различных постановках:

• -    моделирование пуска без учета геометрии носителя и его движения под водой;

• -    моделирование пуска с учетом параметров движения носителя и его геометрии.

Численное моделирование проводилось на основе метода контрольного объема (МКО) [1, 2] с учетом многофазности среды и наличия силы тяжести. Межфазовое взаимодействие учитывается посредством однородной модели Эйлера и модели свободной поверхности -данная комбинация используется для течений с ярко выраженной свободной поверхностью раздела фаз. Эта модель пытается напрямую разрешить поверхность раздела между фазами, помещая в нее специальное граничное условие. Решается один набор уравнений для каждой из фаз и отдельно рассчитывается граница, взаимодействия фаз [3]. Выбор данной комбинации моделей связан с их относительной простотой и вычислительной эффективностью, при этом точность получаемого решения, для данного типа, течений, удовлетворительна. Сравнение, проведенное в ходе тестирования, показало, что при практически сходных результатах временные затраты на. решение задачи с использованием неоднородной модели фаз Эйлера, в среднем в 1,5 раза, больше.

Решение проводилось в нестационарной постановке с использованием гексаэдрических и тетраэдрических сеточных моделей.

В качестве модели турбулентности принималась модель Ментера. - SST [4, 5] - в данном случае на. форму поверхности каверны и ее формирование может оказать существенное влияние пограничный слой на. стенке, поэтому для более точного его моделирования и была, выбрана, данная модель.

При решении задачи вводились следующие допущения:

• -    торпеда, представляет собой неподвижный цилиндр постоянного диаметра, по сечению;

• -    в качестве газовой фазы принимается воздух - идеальный газ. Теплообмен между жидкой и газообразной фазами отсутствует;

• -    вследствие наличия плоскости симметрии задача, решалась в симметричной постановке только для половины модели с целью экономии вычислительных ресурсов.

В первом расчетном случае форма, поверхности носителя не учитывалась, вместо этого бралась плоская стенка, у основания торпеды, вследствие этого не учитывалось и движение носителя.

В связи с простотой геометрии расчетная сетка, строилась с гексаэдрической структурой со сгущениями к твердым поверхностям. Также для лучшего разрешения свободной

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ поверхности газового пузыря производилось сгущение сетки в области основания торпеды.

На рис. 2 представлена расчетная область с конечно-элементной сеткой и схемой задания граничных условий.

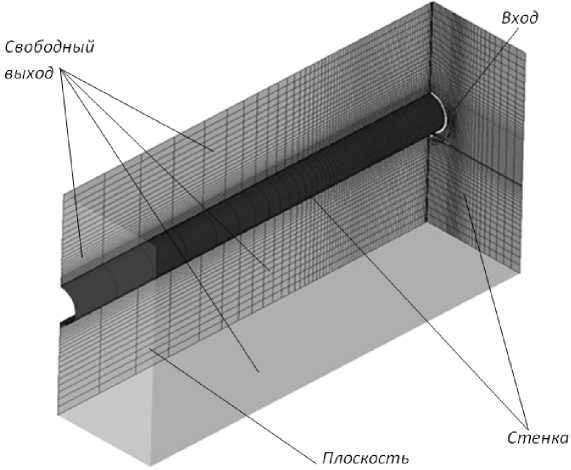
Рис. 2. Расчетная модель и конечно-элементная сетка

Так как расход газовой фазы в кольцевом зазоре зависит от времени, то задание граничного условия входа осуществлялось с помощью кусочной функции, представленной на рис. 3.

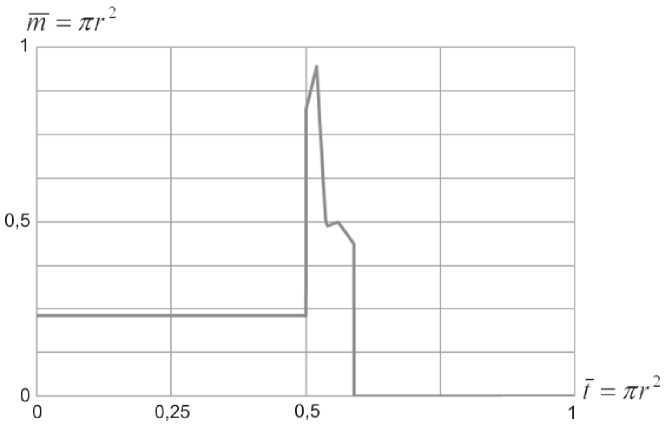
Рис. 3. Расход газа при раскупорке

Момент выхода кормовой части торпеды из пускового устройства соответствует моменту времени t = 0 , 5 . При этом наличие расхода до раскупорки соответствует проникновению газа через обтюрацию между корпусом торпеды и пусковым аппаратом.

В.Г. Дегтярь, В.И. Пегов, Е.С. Меркулов

Размерность задачи составила 275 тысяч ячеек. Шаг по времени варьировался для получения наиболее быстро сходящегося решения, число Куранта не превышало при этом и = 25 .

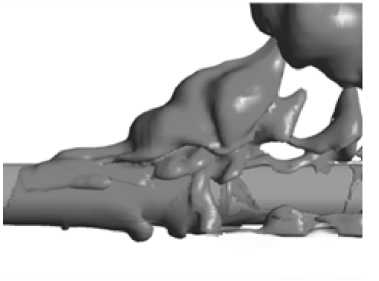
На рис. 4 представлена полученная в ходе решения изоповерхность границы раздела газообразной и жидкой фаз в различные моменты времени. Таким образом, можно проследить эволюцию каверны в зависимости от времени.

t = 0 , 25                                                    t = 0 , 5

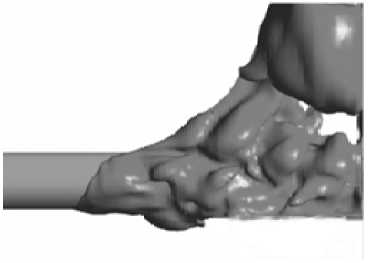
t = 0 , 75

Рис. 4. Граница раздела фаз в различные моменты времени

Как видно из рисунков, в начальные моменты времени (до раскупорки) формируется значительный по своему объему пузырь. Основная его масса находится над торпедой и прилипает к твердой стенке у основания. При этом часть пузыря распространяется вдоль оси торпеды (по-видимому, благодаря силам поверхностного натяжения) с незначительной скоростью. При резком возрастании расхода газа, из-за большой скорости истечения (значительно большей, чем скорость всплытия), часть пузыря, охватывающая торпеду, резко увеличивается в объеме. Необходимо отметить, что к этому моменту верхняя часть пузыря не успевает оторваться от общей массы газа и соединяется с ней узким « каналом » , через который она продолжает подпитываться газом. Благодаря большой скорости истечения газа часть пузыря, примыкающая к торпеде, значительно продвигается в осевом направлении.

После прекращения истечения газа из зазора каверна быстро разрушается на более мелкие структуры, однако часть газообразной фазы продолжает двигаться вдоль оси торпеды.

Контроль достоверности результатов осуществлялся посредством сравнения расчетного давления в заданной точке, находящейся на торпеде на некотором расстоянии от граничного условия входа по направлению движения торпеды, с данными экспериментальных исследований.

На рис. 5 представлен график зависимости давления от времени в расчетной точкев сравнении с экспериментом. На графике хорошо видно волновое « поведение » давления

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ после раскупорки, также заметно, что амплитуда волн со временем уменьшается. Уменьшение амплитуды не носит какого-либо выраженного функционального характера вследствие резкого колебания расходной характеристики на входной границе. Также хорошо видно значительное расхождение с экспериментальными данными как по амплитудам, так и по фазам волн.

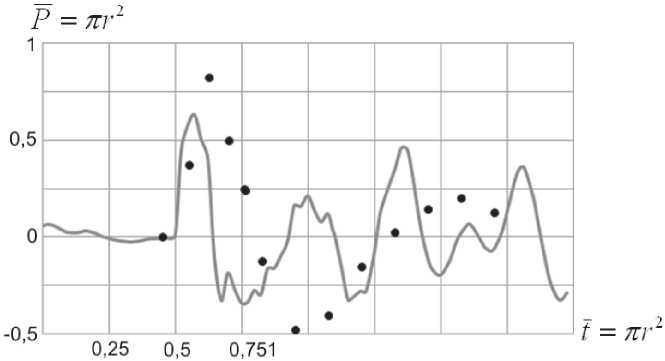
Рис. 5. Давление в расчетной точке на теле. Сравнение с экспериментом (точки -данные эксперимента)

Для оценки влияния геометрических параметров расчетной модели на образование и рост газовой каверны при численном моделировании пуска торпеды, расчеты проводились с использованием уточненной геометрии. Учитывалась форма поверхности носителя, в области пускового устройства присутствует технологическая ниша.

На рис. 6 представлена расчетная область с конечно-элементной сеткой и схемой задания граничных условий.

Расчетная конечно-элементная сетка - тетраэдрическая. Такой тип сетки выбран исходя из того, что геометрия модели значительно усложнилась - появились острые углы, в области ниши, примыкающие к криволинейной поверхности носителя.

Расход газовой фазы в кольцевом зазоре задавался аналогично предыдущему расчетному случаю.

Для моделирования пограничного слоя задавалось сгущение сетки к твердым поверхностям. Также для лучшего разрешения свободной поверхности газового пузыря производилось сгущение сетки в области газовой каверны.

Размерность задачи составила 285 тысяч ячеек. Шаг по времени варьировался для получения наиболее быстро сходящегося решения, число Куранта не превышало при этом Си = 20 .

В данном расчетном случае присутствует начальное движение жидкой фазы, следовательно, чтобы не производить дополнительного временного счета для получения установившегося обтекания носителя, выполнено предварительное приближение. Произведен стационарный однофазный расчет обтекания модели водой.

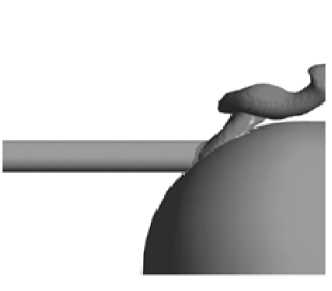
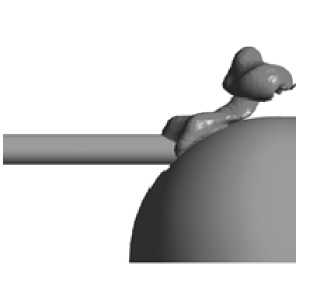
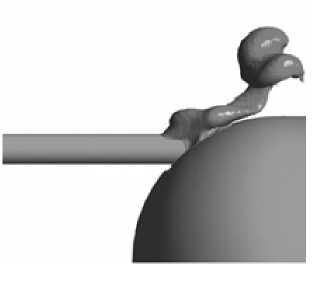
На рис. 7 представлена полученная в ходе решения изоповерхность границы раздела газообразной и жидкой фаз в различные моменты времени.

Как видно из рисунков, в начальные моменты времени формируется значительный по своему объему пузырь. Однако из-за наличия движения жидкой фазы он сносится потоком, при этом скорость сноса равна и даже выше скорости всплытия пузыря. Основная масса каверны находится над поверхностью носителя, прилипая к ней. Вдоль оси торпеды

В.Г. Дегтярь, В.И. Пегов, Е.С. Меркулов

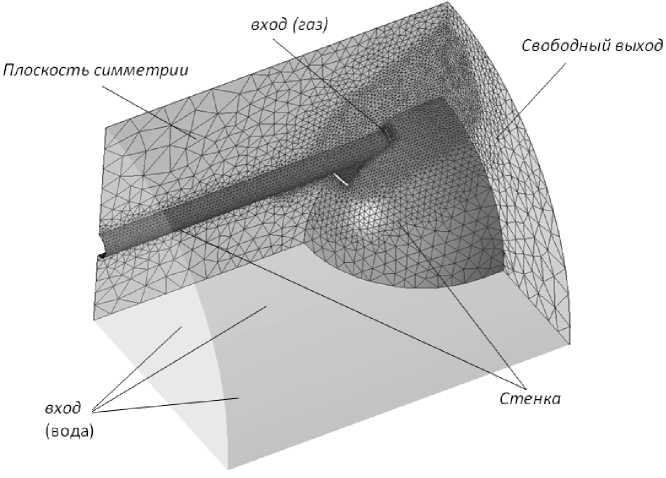
Рис. 6. Расчетная модель и конечно-элементная сетка

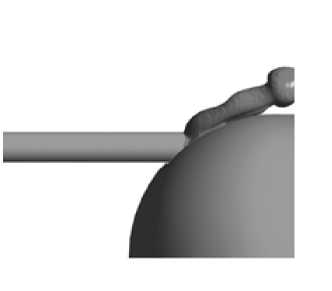
t = 0 , 25

t = 0 , 5

t = 0 , 75

t = 1

Рис. 7. Граница раздела фаз в различные моменты времени газ практически не распространяется, занимая при этом объем ниши, в котором до этого присутствовало замкнутое вихревое течение жидкости. При резком возрастании расхода в зазоре пузырь заполняет весь объем ниши и натекает на верхнюю часть торпеды. Необ-

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ходимо отметить, что, несмотря на то, что время формирования начального пузыря было увеличено к моменту раскупорки, верхняя часть пузыря все еще не успевает оторваться от общей массы газа и после раскупорки также продолжает подпитываться газом. В данном случае это происходит из-за того, что в связи с наличием течения жидкой фазы структура каверны становиться более упорядоченной.

На рис. 8 представлен график зависимости давления от времени в расчетной точке, в сравнении с экспериментом. В данном варианте получено значительно лучшее совпадение с экспериментом, амплитуда волны сжатия превышает экспериментальные данные на ~ 8 % , а волны разряжения меньше на ~ 28 % . Также наблюдаются сдвиг по фазе (при численном моделировании волновой процесс развивается быстрее) и отсутствует нарастание давления после прохождения волны разряжения.

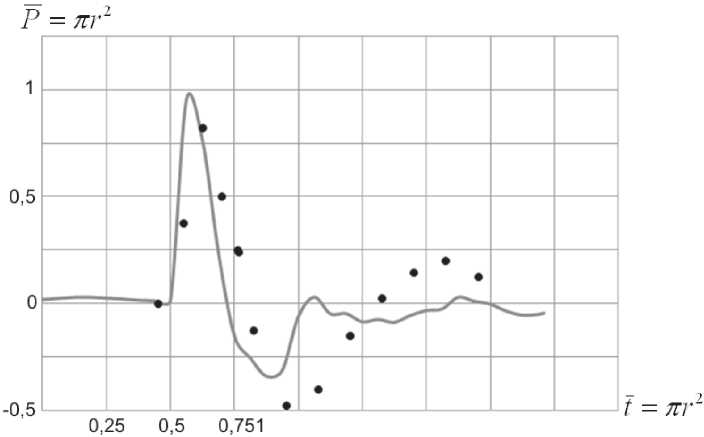
Рис. 8. Давление в расчетной точке на теле. Сравнение с экспериментом (точки -данные эксперимента)

Заключение

В работе представлены методика и результаты математического моделирования эволюции газовой каверны, образующейся при пуске торпеды из горизонтального пускового устройства с борта носителя для двух расчетных случаев.

Получены картины эволюции газовой каверны во времени для всех вариантов расчетов, а так же приведено сравнение давления в заданной точке в каверне с экспериментом.

Уточнение параметров расчетной модели значительно влияет на параметры течения и позволяет получать результаты, удовлетворительно согласующиеся с данными экспериментальных исследований.