Численное моделирование когерентных структур при распространении примеси в атмосферном пограничном слое над лесным пологом

Изучение физических процессов, связанных с воздушным течением над лесным пологом, представляет значительный интерес в связи с различными экологическими приложениями. Формирование лесного микроклимата, осаждение и распространение пыли и других взвесей — примеры важных направлений исследований. До появления высокопроизводительных вычислительных ресурсов исследования в этой области основывались, в основном, на экспериментах, а также двумерных полуэмпирических

моделях. В настоящее время ведутся активные исследования, связанные с расчетами трехмерного турбулентного атмосферного течения над лесным пологом, и, как показывают результаты, турбулентное течение воздуха над лесным пологом существенно неоднородно; важную роль в его формировании играют когерентные структуры, характерный размер которых сравним с высотой полога растительности. До середины девяностых годов прошлого века существовало представление, что такое течение аналогично течению в турбулентном пограничном слое. В настоящее время считается, что основные характеристики течения воздуха вблизи полога растительности аналогичны соответствующим величинам сдвигового течения (mixing layer flow) [1]. Сила трения со стороны растительности приводит к тому, что средняя скорость под пологом меньше скорости над пологом, а вертикальный профиль средней скорости содержит точку перегиба [2]. Характерные турбулентные когерентные структуры, которые образуются на уровне границы полога растительности, возникают благодаря развитию неустойчивости Кельвина–Гельмгольца. При эволюции структур их форма существенно изменяется, и в развитом атмосферном турбулентном течении преобладают структуры, вытянутые вдоль направления течения. Эксперименты с различными видами растительности (злаки, кустарники, деревья) показали, что можно установить некоторый универсальный эмпирический закон, связывающий горизонтальный размер когерентных структур с характерной сдвиговой длиной в вертикальном направлении [3].

Для численного моделирования атмосферного течения над пологом растительности широко применяются различные модификации двух основных методов: моделирования крупных вихрей (Large Eddy Simulation — LES) и решения нестационарных осредненных уравнений Рейнольдса–Навье–Стокса (Unsteady Reynolds–Averaged Navier Stokes — URANS). Поскольку в настоящей работе используется метод LES, то следует остановиться на нем подробнее.

Впервые LES предложен в работе [4] для моделирования течения над лесным пологом и развит в [5]. В исследовании [6] рассматривается течение нестратифицированного воздуха над пологом относительно «редкого» леса; основные статистические характеристики турбулентного течения сравниваются с экспериментальными данными [7]. В настоящей работе также приведено сравнение экспериментальных результатов [7] c результатами численного моделирования. Метод LES позволяет моделировать перенос пассивной примеси. Так в работе [8] изучается влияние турбулентного атмосферного течения над однородным лесным пологом на распределение концентрации примеси, при этом для определения характеристик когерентных структур применяется вейвлет–анализ. Примерами примесей, переносимых воздухом, могут быть пыль, пыльца, сажа от лесного пожара и тому подобное. Например, в работе [9] исследуется распространение пыльцы генетически модифицированных растений и приводится сравнение результатов с экспериментом. Метод моделирования крупных вихрей позволяет идентифицировать когерентные структуры в развитом турбулентном течении [10]. Характерная структура имеет вид пары вихрей, вытянутых в направлении течения и вращающихся в противоположных направлениях. Впервые она была описана в работе [11], авторы которой применили метод эмпирических ортогональных функций (Empirical Orthogonal Function — EOF) к обработке результатов измерений в аэродинамической трубе. На основе анализа экспериментов с различными типами растительности в работе [12] сделаны важные выводы о характеристиках когерентных структур.

Цель настоящей работы заключается в том, чтобы в результате моделирования крупных вихрей улучшить понимание физических механизмов, определяющих атмосферное турбулентное течение и перенос примеси над лесным пологом. Особое внимание уделяется этапам формирования развитого турбулентного течения при эволюции волн Кельвина–Гельмгольца. Используется математическая модель, аналогичная [8], с дополнительным кинетическим уравнением для концентрации примеси; примесь предполагается связанной с элементами растительности. Авторам не известны другие работы, где рассматривалось бы такое дополнительное уравнение.

2.    Математическая модель

Основными уравнениями для моделирования динамики крупных вихрей (LES) турбулентного течения над лесным пологом, являются уравнения Навье–Стокса и уравнение неразрывности. Осредненные по пространству таким образом, чтобы исключить мелкомасштабные возмущения, они имеют вид [8]:

д U;

т ^- = 0, дx j

£(p      x(p uu ) ц l

д дxj

(д и, дu , )

+ ^-

^д x j д x _V

д P дт — + — ^- д x i д x j

1/2

a L C D P ( ^U-^U- )

u_i ,

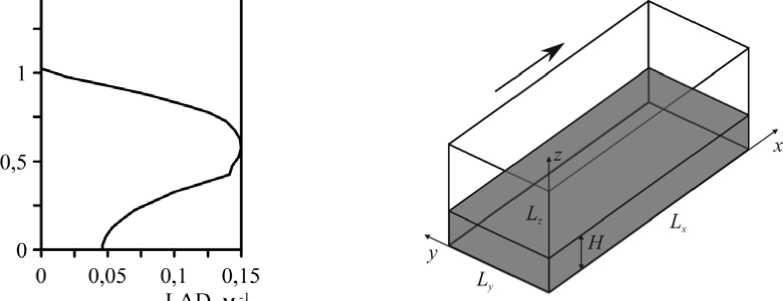
где ui — пространственно осредненная i -я компонента скорости (далее u — x–компонента скорости, w — z–компонента скорости), P — давление, p — средняя плотность воздуха, Tj — тензор напряжений Рейнольдса, цL — вязкость воздуха. Уравнение (2) содержит силу сопротивления, пропорциональную квадрату скорости, коэффициенту аэродинамического сопротивления со стороны лесного массива — CD (CD = 0,15), и удельной поверхности растительности — aL . Распределение aL (Leaf Area Density — LAD), однородное в горизонтальном направлении и неоднородное по вертикали, соответствующее экспериментальным

H данным [7], представлено на рисунке 1, а. Величина LAI =   aLdz (Leaf Area Index —

LAI) определяет общую поверхность элементов растительности в объеме, имеющем высоту H и единичную площадь основания. В настоящей работе LAI = 2.

В рамках выбранной модели турбулентности для тензора напряжений Рейнольдса используется следующая параметризация:

Т- = ij

3 ^P k ^ у ^{+ Ц} T

(д и,   д u , )

+ ^j дx,   дx, ji

Ц T = P C ц L SGS V k ,      L SGS = (A x А у ^А z ) ^1/3 ,        ⁽³⁾

где к — удельная кинетическая энергия турбулентности, 5- — символ Кронекера, ц T — турбулентная вязкость, Cц — феноменологический коэффициент (Cц = 0,07), Lsgs — характерный подсеточный масштаб (SubGrid-Scale — SGS), Ax Ау Az — элементарный объем вычислительной сетки. Опыт приложения единого выражения для турбулентной вязкости к расчетам атмосферного турбулентного течения внутри и над лесным пологом различными авторами, а так же сопоставление результатов численного моделирования с экспериментальными данными показывают, что выбранное приближение достаточно неплохо работает [6], [7]. Уравнение, описывающее эволюцию турбулентной кинетической энергии, имеет следующий вид:

д Z  ,х д Z  , X д [_    ( дк ]) дU     п к3/2    , _ z

— (Pk ) + ^(P kU-)=^ 2Ц T      +Т ij^ -P CE~T--2 aLCD P( u-uj) k д t дx,        ;   дx,. дx,. дx; L(< x7

j               j v V - V /         -

Уравнение (4) представляет собой типичное уравнение переноса. Кроме конвективного и диффузионного слагаемых в правой части оно содержит три источниковых слагаемых, которые, соответственно, описывают производство турбулентной кинетической энергии, ее диссипацию в мелкомасштабные структуры и трение со стороны лесного массива (величина коэффициента трения C _Е = 0,93 обсуждается в работе [8]). Предполагается, что характерный масштаб течения, индуцируемого обтеканием отдельного дерева, меньше характерного размера выбранной расчетной сетки, то есть выбранная модель (1)–(4) не описывает столь мелкомасштабные вихри турбулентного течения.

Для моделирования переноса пассивной примеси использовалась модель, аналогичная применяемой в работе [8]:

-(р с )+— д Г ’ дx j

д C

(р UjC ) = —

' дx j V Sc V д x

1/2

- c C a L ^P ( u j u j ) ^{( C} - ^C ref ) ,

V

где C — концентрация примеси, Sc — число Шмидта для подсеточных процессов (Sc = 1/3), c _C — эмпирический коэффициент, характеризующий скорость обмена концентрации примеси, содержащейся в воздухе ( c _C = 0,04), с концентрацией C _ref , связанной с элементами растительности лесного полога. Были проведены расчеты, в которых связанная концентрация полагалась постоянной ( C _ref = const), а C _ref удовлетворяло следующему кинетическому уравнению:

T^ t ( P ^C ref ) = c C a L P ( u j u j ) ^1/2 ( ^C - ^C ref ) .                                                            ⁽⁶⁾

Значения входящих в обсуждаемую математическую модель (1)–(6) эмпирических коэффициентов C D , C _ц , C _E , c _C взяты из работы [8].

3.    Численный метод и параметры задачи

Расчеты проводились с помощью программного пакета FireStar 3D [11], который ориентирован на моделирование поведения лесных пожаров. Уравнения задачи (1)–(6) сводились к уравнениям переноса, дискретизация которых получалась при помощи метода конечных объемов с использованием однородной разнесенной сетки для полей давления и скорости. Для пространственной аппроксимации конвективных слагаемых применялась схема QUICK c ограничителями потока; аппроксимация диффузионных слагаемых осуществлялась по схеме с центральными разностями. Эволюция во времени находилась неявным методом Эйлера третьего порядка с переменным шагом по времени. Алгоритм класса PISO [14] обеспечивал согласованное вычисление полей скорости и давления. Система линейных алгебраических уравнений, получающихся при дискретизации уравнения переноса, решалась при помощи метода BiCGStab с ILU предобуславливателем; для решения симметричной системы уравнений и определения давления применялся метод сопряженных градиентов.

Параллельные вычисления на основе технологии OpenMP [11] производились на ЭВМ SGI ALTIX 350, обладающей общей памятью с неоднородным доступом (Non-uniform Memory Access). Каждый из 10 вычислительных узлов содержал 2 процессора Intel Itanium2 (1,5 ГГц, L3-cache 4 Мб) и 4 Гб локальной оперативной памяти.

z/H 1,5

а                                         б

Рис. 1. Вертикальное распределение относительной поверхности растительности LAI ( a ) и расчетная область задачи ( б )

Расчеты проводились для области, представляющей собой прямоугольный параллелепипед с размерами L_x = 300 м, L_y = 100 м, L_z =80 м (Рис. 1, б ). Высота лесного полога, занимающего нижнюю часть вычислительной области, равнялась H = 20 м. На боковых границах выполнялись условия периодичности для всех рассматриваемых полей. На нижней границе для скоростей использовались условия со стандартными функциями теории пристеночной турбулентности. На верхней границе области задавалась постоянная величина скорости U_x = 12 м/с. Для турбулентной кинетической энергии на верхней и нижней поверхностях вычислительного домена выполнялись однородные граничные условия Неймана. Для вычислений строилась однородная сетка с числом узлов N_x = 150, N_y = 50, N_z = 80, шаг интегрирования по времени составлял Δ t = 0,01 с. С ростом размеров расчетной области увеличивалось время вычислений, но размеры области не влияли на исследуемые когерентные структуры, вытянутые в направлении течения. Область также имела форму, вытянутую в направлении течения. Рассматриваемый лесной полог считался однородным в x , y направлениях, что позволяло задать периодические граничные условия. Следует заметить, что периодические граничные условия используются и в других работах, например в [8]. Величина параметра L SGS ( L SGS = 1,59 м) выбиралась таким образом, чтобы он лежал в инерционном интервале спектра турбулентного течения. Для оценки считалось, что длина, в 10 раз меньшая крупномасштабных неоднородностей течения, принадлежит инерционному интервалу. В задаче об атмосферном течении над лесным пологом крупномасштабные структуры имели размеры порядка высоты лесного полога H .

4.  Динамика течения. Результаты

Процесс формирования развитого турбулентного течения над лесным пологом более схож со сдвиговым течением, чем с течением в пограничном слое. Поскольку со стороны лесного массива действует сила сопротивления, в этой области средняя скорость течения уменьшается. Вертикальное распределение средней скорости содержит точку перегиба на уровне верхней границы лесного полога, что свидетельствует о наличии гидродинамической неустойчивости. Её развитие приводит к формированию волн Кельвина–Гельмгольца.

Для визуализации трехмерных структур при исследовании турбулентных течений используется скалярная величина Q — инвариант тензора градиента скорости V i u j , которая была впервые предложена в работе [15]:

о ut

V ⁹ x J

^

dх,.        15х..d iji

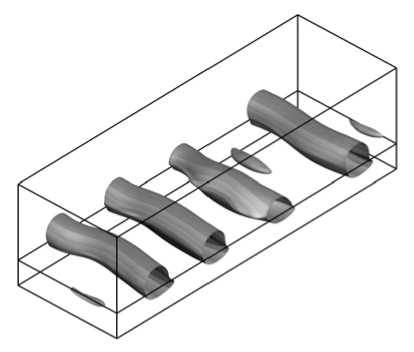
В областях, где критерий Q положителен, разность между завихренностью и сверткой тензора скоростей деформации также положительна; здесь будет преобладать вихревое движение. Так изоповерхности Q на рисунке 2, а описывают структуру волн Кельвина–Гельмгольца, которые возникают на уровне верхней границы лесного полога и переносятся окружающим воздушным потоком. Поперечные валы Кельвина– Гельмгольца, вращающиеся в одном направлении, формируют характерную «волнообразную» структуру в распределении турбулентной кинетической энергии, максимальное значение которой наблюдается вблизи границы полога леса.

Важной характеристикой исследуемого течения является сдвиговая длина (mixing length) — LS = U ( H ) / ( dU / dz ) _H , где U — величина средней по времени х -компоненты скорости. Сдвиговая длина определяет характерный масштаб в вертикальном направлении вблизи границы полога леса, на котором проявляются эффекты, вызванные существованием точки перегиба в профиле скорости. Другой величиной, описывающей неустойчивость Кельвина–Гельмгольца, служит длина волны возникающей структуры — Л^. Продолжая аналогию со сдвиговым течением, необходимо отметить следующий факт: в работе [16] в рамках линейной теории гидродинамической устойчивости для невязкого характерного сдвигового течения получено соотношение Л^ = 15,6 L S , которое неплохо согласуется с результатами вычислений на начальной стадии развития турбулентного течения.

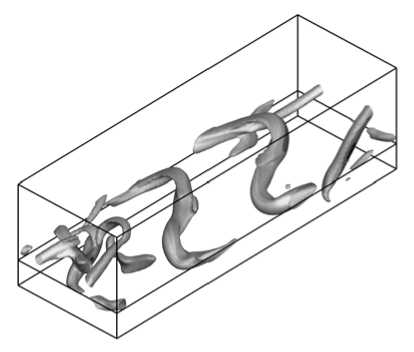
Следующий шаг в эволюции воздушного течения над лесным пологом — это возникновение и развитие вторичной неустойчивости, которая приводит к искривлению волн Кельвина–Гельмгольца и формированию зигзагообразных структур (Рис. 2, б ). Характерное расстояние между продольными валами становится сравнимым с характерным расстоянием между поперечными валами, а системы перпендикулярных валов переплетаются друг с другом. Подобная пространственная структура (vortex lattice structure), впервые описанная в работе [17], развивается в сдвиговом турбулентном течении и обладает похожими свойствами.

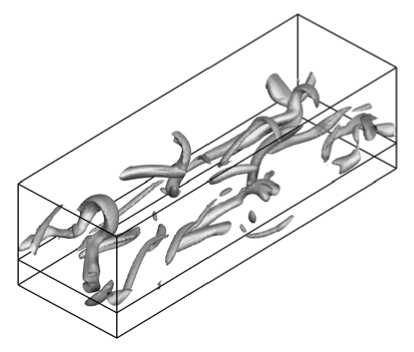
По мере развития турбулентного течения в областях между валами Кельвина– Гельмгольца формируются вихри, вытянутые в направлении течения (hairpin vortices). На рисунке 2, в изображены изоповерхности Q , на примере которых можно наблюдать преобладание продольных вихрей. Кроме того, в течении возникает подковообразная когерентная структура (horseshoe vortex), характерная для пограничных турбулентных слоев (Рис. 2, в ).

Обобщение экспериментальных данных указывает на то, что в развитом турбулентном течении над лесным пологом важную роль играют крупномасштабные когерентные структуры, вытянутые вдоль направления течения. Характерный продольный размер таких структур Л Х^ связан со сдвиговой длиной L S соотношением: Л Х²⁾ /LS = 8,1 . Существенно, что для развитого сдвигового турбулентного течения

а

б

в

Рис. 2. Этапы формирования когерентных структур; поверхности уровня критерия Q в различные моменты времени t , с: 90 ( а ); 150 ( б ); 170 ( в ); 200 ( г )

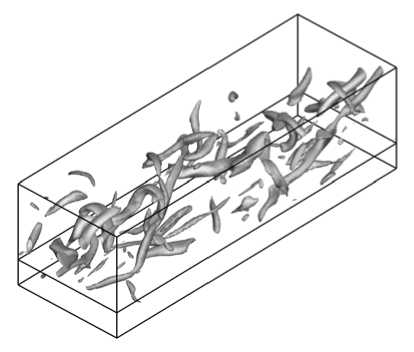
г

указанное отношение составляет [3] Л(,²⁾ / L S = 7 ^ 10 и согласуется с результатами расчетов настоящей работы (Рис. 2, г ), что служит еще одним аргументом, подтверждающим аналогию между исследуемым течением и сдвиговым течением. Следует отметить, что в работе [3] в общих чертах обсуждалась аналогия сдвигового турбулентного течения и атмосферного течения над лесным пологом, однако численное моделирование последовательных этапов формирования развитого атмосферного течения и сопоставление результатов со сдвиговым течением производится впервые.

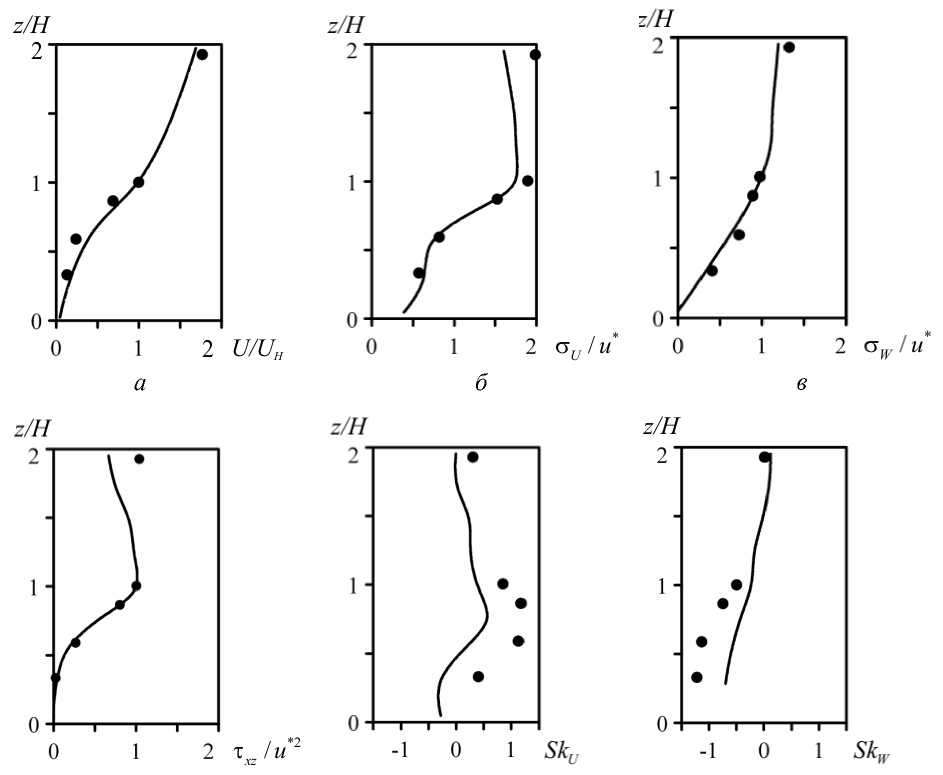
Конфигурация расчетной области и параметры задачи подобраны таким образом, чтобы стало возможным сравнение с экспериментами, проведенными ранее [7]; подобное сопоставление предпринималось также в работе [6]. На рисунке 3 приведены распределения статистических характеристик развитого турбулентного течения, которые неплохо согласуются с экспериментальными данными. Как уже отмечалось, безразмерный вертикальный профиль средней горизонтальной скорости течения U(z) / U(H) содержит точку перегиба на уровне z = H, где сдвиговое напряжение достигает максимального значения (Рис. 3, а). Согласно работе [18], при выполнении условия LAI х CD > 0,1 атмосферное течение над лесным пологом имеет больше общих черт со сдвиговым течением, чем с течением в пограничном слое. Поскольку в приведенном расчете параметр LAI х CD равен 0,3 и наблюдается аналогия со сдвиговым течением, тем не менее слабовыраженная точка перегиба на рисунке 3, а и присутствие подковообразных когерентных структур указывают на общие черты изучаемого течения с течением в пограничном слое. Показанные среднеквадратичные отклонения горизонтальной (Рис. 3, б) и вертикальной (Рис. 3, в) скорости, а также xz–компонента тензора напряжений Рейнольдса (τxz = -u′w′ ) (Рис. 3, г) нормированы на характерную величину u*=τxz (H) (friction velocity). Распределение дисперсии скоростей указывает на то, что внутри лесного полога интенсивность турбулентного течения увеличивается с высотой и достигает характерных значений σU /u*∼ 2 и σW /u*∼ 1 над лесным пологом [3]. Статистические моменты третьего порядка для горизонтальной и вертикальной скорости (skewness) SkU= u′3/σU3, SkW=w′3/σW3 изображены на рисунке 3 (см. фрагменты д и е). Присутствие области с положительными (SkU ) и отрицательными (SkW ) значениями внутри лесного полога можно объяснить преобладанием порывов ветра с положительными отклонениями горизонтальной скорости и отрицательными отклонениями вертикальной скорости (ejections) [3]. Над лесным пологом моменты третьего порядка обращаются в нуль, распределение скоростей соответствует симметричному распределению Гаусса.

д

е

г

Рис. 3. Вертикальные профили статистических характеристик турбулентного течения (сплошная линия – результаты вычислений, • – экспериментальные данные): средняя скорость течения ( а ), среднеквадратичное отклонение горизонтальной ( б ) и вертикальной ( в ) скоростей, xz –компонента тензора напряжений Рейнольдса ( г ), момент третьего порядка для горизонтальной ( д ) и вертикальной скоростей ( е )

Таким образом, можно утверждать, что представленные результаты численного моделирования (Рис. 3) неплохо соответствуют экспериментальным результатам. Значительно расходятся лишь статистические моменты третьего порядка (Рис. 3, д и е ). Аналогичное поведение наблюдалось и в работе [6], где величины Sk_U и Sk_W составляют около 50% от величин, полученных в эксперименте. Авторы объясняют такое поведение ограничениями, которые возникают в LES из-за конечных размеров вычислительной сетки. Другой причиной расхождения может быть ограниченность промежутка времени, в течение которого проводилось осреднение результатов расчетов.

5.    Распространение концентрации примеси. Результаты

При численном моделировании распространения концентрации пассивной примеси в атмосферном течении над лесным пологом на основе уравнений (5), (6) начальное распределение концентрации в атмосфере равнялось нулю ( C 0 = 0 ). Источником примеси служила связанная концентрация, распределенная на поверхности растительности, при этом вертикальный профиль C _r ⁰ _ef задавался пропорциональным удельной поверхности растительности a_L ( C 0_f = a_L х 10 " ⁵ ). Изучение распространения примеси начиналось с момента времени t ⁰ = 10³ с, к которому течение достигало развитого турбулентного режима.

Представленные результаты (Рис. 4) соответствуют двум ситуациям: I — связанная концентрация остается постоянной (подобная ситуация рассматривалась в работе [8]); II — связанная концентрация изменяется в соответствии с законом (6) (в такой постановке задача ранее не решалась). Распределения концентрации показаны в плоскости у = 0,5 L y в различные моменты времени. Как видно из рисунка, первоначально в обеих ситуациях максимальное значение концентрации примеси наблюдается на уровне z = 0,5 H , где распределение связанной концентрации C ref имеет максимум. Изолинии концентрации на фрагментах 4, а и 4, б изображены в одном масштабе, и можно заметить, что концентрация в атмосфере в ситуации I достигает больших значений, чем в ситуации II Кинетическое уравнение для связанной концентрации (6) обуславливает быстрое уменьшение количества примеси, содержащейся на элементах растительности в лесном пологе. В результате источниковое слагаемое в уравнении (5), ответственное за перемещение примеси с элементов растительности в атмосферу, для ситуации II уменьшается быстрее, чем в ситуации I.

Следует обратить внимание на характерные структуры в распределении концентрации при t = 300 с (Рис. 4, а ). Они имеют вид горбов, наклоненных под углом 45° к направлению течения, при этом концентрация в нижней части области превосходит концентрацию в верхней части; подобные распределения наблюдались и в работе [8]. Структуры распределения концентрации формируются за счет структуры самого течения; в данном случае форма микрофронта примеси указывает на возникающие в турбулентном пограничном слое стики (steak). Эти когерентные структуры, представляющие собой высокоскоростные области пристеночного течения, взаимодействуют с внешними частями течения и играют важную роль в процессах переноса между лесным пологом и атмосферой. Подробнее обсуждение механизмов формирования стриков в турбулентном пограничном слое содержится в работе [19].

Суммарная концентрация примеси в рассматриваемой области может изменяться только благодаря источниковому слагаемому в уравнении (5), поскольку на боковых границах области поддерживаются периодические условия и поток примеси на верхней и нижней границах равен нулю. В ситуации I, когда концентрация связанной примеси

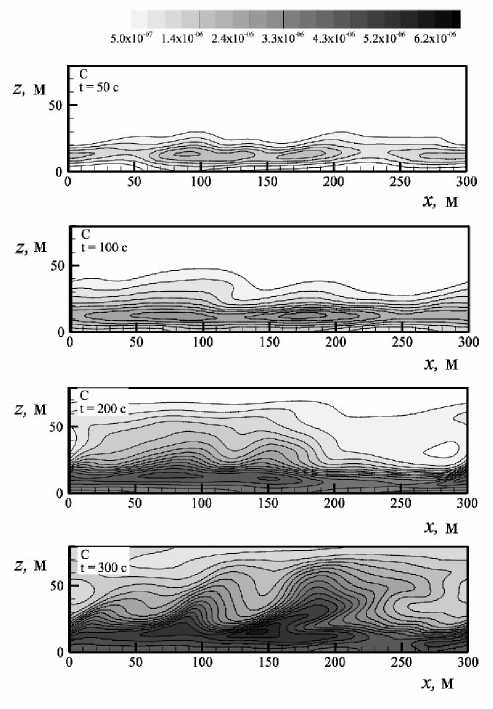
а

Рис. 4. Распределения концентрации пассивной примеси в атмосфере в плоскости y = 0,5 L y в различные моменты времени для двух ситуаций: фиксированная ( а ) и изменяющаяся ( б ) концентрация связанной примеси

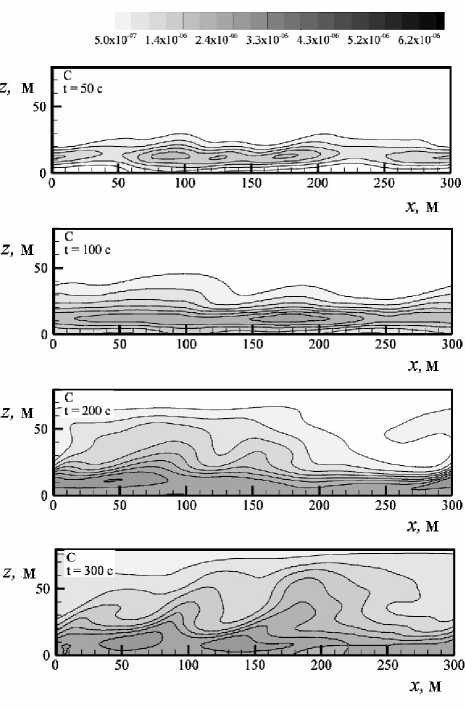
б

( C _ref ) остается постоянной, суммарная концентрация примеси в атмосфере растет со временем, начиная с нулевого значения. В ситуации II суммарная концентрация примеси в атмосфере растет со временем, а суммарная связанная концентрация уменьшается, поскольку примесь «вымывается» течением из лесного полога. В соответствии с законом сохранения в ситуации II следует ожидать, что общее количество концентрации, распределенной в атмосфере и на элементах растительности, будет оставаться постоянным. Результаты расчетов согласуются с этим утверждением; относительное изменение суммарной концентрации за 800 c составляет порядка 0,2%.

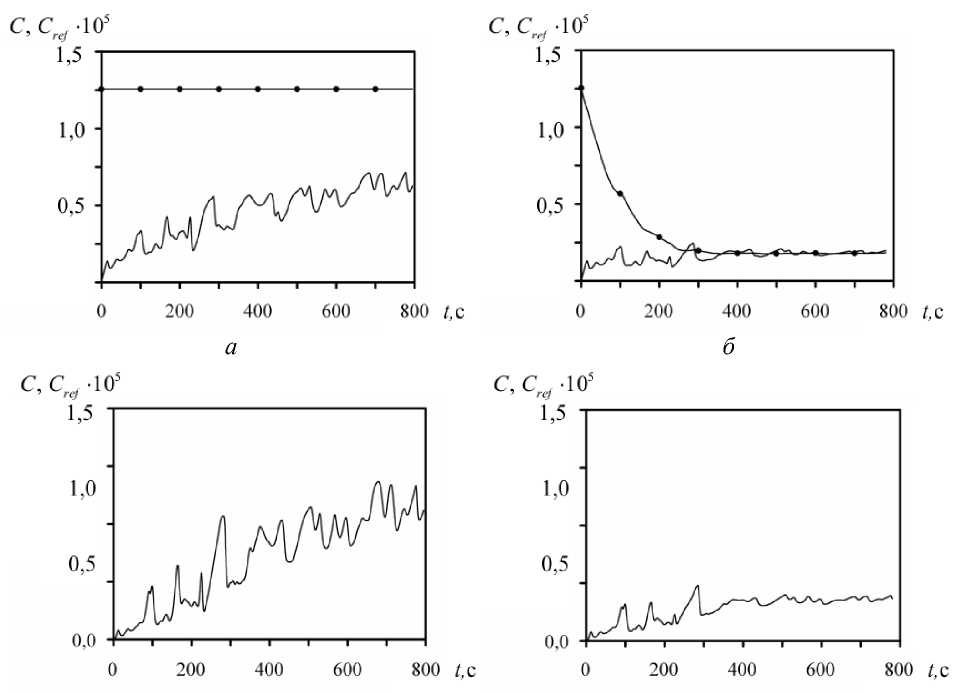
Эволюция во времени концентрации примеси в атмосфере и связанной концентрации изображена на рисунке 5 для ситуаций I и II в точках z = 0,8 H и z = 1,3 H . В точке z = 0,8 H (Рис. 5, а ) интенсивность турбулентного течения меньше, чем в точке z = 1,3 H , на что указывает амплитуда колебаний концентрации. На рисунке 5, б можно заметить тенденцию к равновесию между концентрацией примеси в атмосфере и связанной концентрацией, возмущения формы кривых вызваны турбулентным характером течения. Как отмечалось, в ситуации II величина концентрации меньше по сравнению с ситуацией I, так на рисунках 5, в и 5, г их отношение отличается в несколько раз.

в

г

Рис. 5. Эволюция во времени концентрации примеси в атмосфере (сплошная линия) и связанной концентрации (линия с крупными точками) на разных высотах.

Ситуация I: z = 0,8 H ( а ) и z = 1,3 H ( в ); ситуация II: z = 0,8 H ( б ) и z = 1,3 H ( г )

6.    Заключение

Задача взаимодействия течения в атмосферном пограничном слое с однородным лесным пологом исследовалась численно на основе метода моделирования крупных вихрей (LES). Результаты указывают на общие черты изучаемого течения с турбулентным течением в сдвиговом слое. Развитие неустойчивости Кельвина– Гельмгольца приводит к образованию поперечных вихрей, дальнейшая эволюция которых формирует характерные структуры, наблюдаемые в развитом турбулентном течении. Известные когерентные структуры сдвигового турбулентного течения впервые получены при численном моделировании атмосферного течения над лесным пологом. Вычисленные статистические характеристики течения неплохо согласуются с экспериментами результатами. Предложена новая модель для описания переноса пассивной примеси между атмосферой и элементами растительности. Если считать, что связанная концентрация не остается постоянной, как это полагалось в предшествующих работах, то характерная величина концентрации примеси в атмосфере достигает существенно меньшего значения.

Работа выполнена при финансовой поддержке Европейского проекта FIREPARADOX (2006-2010).