Численное моделирование конечно-амплитудных пространственных возмущений адвективного термокапиллярного течения в слабо вращающемся слое жидкости в условиях микрогравитации

Адвективные термокапиллярные течения в слое несжимаемой жидкости возникают вследствие неоднородности температуры на его границах, перпендикулярных направлению силы тяжести, то есть от воздействия продольного градиента температуры [1, 2]. Так, согласно [1], устойчивое термокапиллярное течение в достаточно тонком слое при действии гравитации образуется в случае, когда на свободной границе поддерживается линейное распределение температуры. При теплоотдаче с поверхности по закону

Ньютона возмущения температуры на поверхности отличны от нуля и, вследствие эффекта Марангони, может появиться неустойчивость течения. При твердой теплоизолированной нижней границе слоя с учетом силы тяжести в отсутствие вращения подобная задача устойчивости решалась в работах [3, 4].

Вращение меняет профиль скорости и температуру течения, что также может привести к неустойчивости течения. Термокапиллярные адвективные течения во вращающемся слое жидкости впервые были описаны аналитически и исследованы в [5]. В [6] исследовалась линейная устойчивость термокапиллярного течения во вращающемся слое жидкости в условиях микрогравитации с твердой теплоизолированной нижней границей; построены нейтральные кривые, отражающие зависимость критического числа Марангони от числа Прандтля для различных значений числа Тейлора. Показана необходимость учета силы Кориолиса при анализе термокапиллярных течений в условиях космического орбитального полета.

В монографии [7] представлен широкий класс замкнутых адвективных течений во вращающемся плоском слое несжимаемой жидкости. Влияние слабого вращения на структуру адвективного термокапиллярного течения в цилиндрическом аппарате с жесткой теплоизолированной нижней границей и свободной верхней границей в условиях микрогравитации изучалось численно в [8, 9]. Поведение пространственных конечно-амплитудных возмущений адвективного течения в слабо вращающемся горизонтальном слое жидкости со свободной верхней и твердой нижней границами рассмотрено в [10]. При сильном вращении и с учетом центробежной силы устойчивость течения рассмотрена в [11].

В работах [12–14] численно исследовано термокапиллярное течение, возникающее в кольцевом зазоре с твердой нижней и свободной верхней границей, с нагретой внешней стенкой и охлажденной внутренней. Расчеты показали, что слабое вращение дестабилизирует течение, а увеличение скорости вращения замедляет начало колебательной неустойчивости.

В [15] впервые представлено точное решение уравнений Навье–Стокса в приближении Буссинеска, характеризующее адвективное термокапиллярное течение в тонком бесконечном слое жидкости со свободными границами в условиях невесомости, принимается во внимание влияние вращения на линейную устойчивость такого течения, численно проанализировано поведение конечно-амплитудных возмущений за пределами порога устойчивости. Показано, что увеличение числа Тейлора стабилизирует течение. Выявлено, что наиболее опасной является монотонная неустойчивость, а за порогом устойчивости конечно-амплитудные возмущения скорости и температуры образуют, соответственно, системы пространственных вихрей и температурных пятен. В случае монотонной линейной неустойчивости возмущения носят стационарный характер, а при колебательной линейной неустойчивости — периодический, зависящий от времени.

В [16] получено новое точное решение уравнений Навье–Стокса, описывающее адвективное термокапиллярное течение в медленно вращающемся слое несжимаемой жидкости со свободными недеформируемыми границами в условиях микрогравитации с учетом касательной термокапиллярной силы Марангони, обусловленной температурной зависимостью коэффициента поверхностного натяжения. В процессе исследования устойчивости адвективного течения рассмотрены пространственные винтовые периодические по длине слоя возмущения в виде валов с осью, перпендикулярной слою, и перпендикулярно направленные пространственные спиральные периодические возмущения в виде валов с осью, параллельной течению. Построены нейтральные зависимости критического числа Марангони от волновых чисел k и k для различных значений чисел Грасгофа и Тейлора и фиксированных значений чисел Прандтля ( Pr = 6,7 ) и Био ( Bi = 0,1 ). Анализ нейтральных кривых показал, что слабое вращение и увеличение гравитационной силы стабилизируют течение. При винтовых возмущениях и малых числах Грасгофа неустойчивость носит монотонный характер, с увеличением гравитационной силы неустойчивость становится колебательной. В случае спиральных возмущений неустойчивость имеет колебательный характер. При малых числах Грасгофа наиболее опасными являются монотонные винтовые возмущения, с увеличением числа Грасгофа угрожающими устойчивости становятся спиральные колебательные возмущения. Данная работа является продолжением исследования такого термокапиллярного течения; в ней рассматривается поведение конечно-амплитудных возмущений, возникающих во вращающемся слое жидкости при значениях числа Марангони выше критического.

2.    Постановка задачи

Рассмотрим плоский бесконечный слой несжимаемой жидкости шириной 2 h , находящийся в условиях микрогравитации и вращающийся с постоянной угловой скоростью о ₀ (Рис. 1). Ось вращения совпадает с вертикальной осью O z декартовой системы координат O xyz . Вертикальная ось направлена противоположно действию силы тяжести. Начало координат расположено в середине слоя. Вращение слабое и позволяет пренебрегать центробежной силой на достаточно небольшом расстоянии от вертикальной оси. Обе границы слоя свободны и считаются плоскими, на них действует касательная

Рис. 1. Плоский горизонтальный слой жидкости шириной 2 h , вращающийся с постоянной угловой скоростью Q_o

термокапиллярная сила Марангони. Коэффициент поверхностного натяжения линейно зависит от температуры T [5]: _а = а_о - у ( т - т ) , где у — температурный коэффициент поверхностного натяжения.

На границах осуществляется теплоотдача по закону Ньютона. Температура среды вблизи границ слоя является линейной функцией координат t = Ax , где A — постоянный горизонтальный температурный градиент. Спектр инерционных колебаний на орбите является неоднородным, но поскольку время развития конвективных возмущений много меньше времени изменения медленно меняющейся компоненты инерционного поля, то будем считать, что находимся в условиях статической микрогравитации (инерционное поле квазистационарно).

Исследование будем проводить на основе безразмерных уравнений д V                    /---

---+ M n( V V ) V + VT a( e_z х V ) = д t

Gr

-V p + А V + --- T e

Mn

div V = 0 ,

д T                      1

---+ M n V • V T = --А T д t                  Pr

с граничными условиями для скорости и температуры

д U     д T

= -     - д z      д x

д V      д T

---= ---- , W = 0,     p = p_Q - const, д z       д у

z = ± 1

д T

---= +Bi( T - x ) . д z

В (1)-(4) в качестве единиц измерения длины, времени, скорости, температуры и давления выбраны, соответственно, h , h ²/v , Ah /p_ov , Ah , y a , где h — толщина слоя, v — коэффициент кинематической вязкости, р₀ — плотность жидкости. Также использованы обозначения: V ( t , x , у , z ) = ( и , V , w ) — вектор скорости; p — давление; t — время; Mn = y Ah ² /p_ov — число Марангони; Ta = ( 2 Q _o h ² /v ) — число Тейлора; Pr = v/x — число Прандтля; Gr = g р Ah ⁴/v ² — число Грасгофа; x — коэффициент температуропроводности; 10 ^{- 5} <  g <  10 ^{- 3} м/с² — ускорение силы тяжести в условиях микрогравитации [17]; в — коэффициент теплового расширения; Bi = bh /p_ov — число Био, b — коэффициент теплоотдачи.

Уравнение состояния в приближении Буссинеска выберем в виде р = р₀ (1 -р T ) и рассмотрим ситуацию, когда число Фруда Fr = Q 2 1 /g ^{< с} 1 , где I — значение характерного горизонтального масштаба ( h ^ I ). В этом случае влиянием центробежной конвективной силы можно пренебречь, поскольку оно компенсируется полем силы тяжести [18].

Для полноты системы уравнений необходимо записать условия замкнутости потока:

Uudz = 0,     f Vdz = 0 .

При граничных условиях (4) во вращающемся слое несжимаемой жидкости формируется однородное по x и у стационарное течение, которое может быть описано аналитически [ 16]. Аналитическое решение для скорости такого течения представляет собой точное решение уравнений Навье-Стокса — это комплекснозначная функция вида:

sh ( X z )     Gr 1   Г       sh( X z ) 1

M ( z ) = ----------+--1 - z + --------I

X ch (X)   Mn X2 [      z ch( X) J где u0 = ReM (z) и v0 = ImM (z). Функция скорости состоит из двух слагаемых, при этом первое характеризует воздействие на движение жидкости поверхностного натяжения, а второе — микрогравитации.

Температурная компонента решения имеет вид:

T 0 = x ^{+ т} 0 ⁽ z ) >

MnPr Г         Bi         1

^т о =     /----- I v о ⁽ z ) ^— --------- v о ^{( 1} ) z I .

V Ta L         1 + Bi        J

• 3.    Конечно-амплитудные возмущения

Поведение возмущений конечной амплитуды в надкритической области исследуется на основе полных нелинейных уравнений конвекции аналогично работам [1, 2]. Пусть г ( u , v , w ) и 6 — конечноамплитудные возмущения скорости и температуры. Тогда для пространственных винтовых периодических по x возмущений нелинейная безразмерная система примет вид:

дф      Г дф дф дф дф

--+ M n ---+--+ д t        L д z д x д x д z

дф          дф 1

и о ( z )----+ и о ( z )-----I д x           д x J

-

I ----д v

V Ta — = Аф д z

-

Gr д6 ^,

M n д x

Аф + ф = о ,

д v        Г --+ M n I — д t          L	дф д v + 5 z д x	дф д v ”ГТ + и о ( д x д z	д v z )г+ д x	-, хдф 1    /~~ и о ( z )    | — VTa д x J		дф ---= А v д z
д6       Г	дф д6	дф д6	д6	дф	, z , дф 1	1
---+ M n I ■	—	+         + и о	( z )----	—	+ т о ( z )----- |	= —А6 ,
д t         L	д z д x	д x д z	д x	д x	д x J	Pr

а граничные условия на z = ± 1 станут следующими:

дб     д v        дб _

ф = о,     ф = ---- ,    --- = о,    --- = ⁺ B i 6 .

д x     д z          д z

В (8)-(12) ф ( t , x , z ) — это функция тока возмущений, а ф ( t , x , z ) — вихрь возмущения скорости, которые связаны с компонентами возмущения скорости соотношениями:

дф          дф         д и д w                  д ²     д ²

и = —    , w =     , ф =    —     = — А ф, А =     +     , д z            д x           д z д x                    д x2 д z2

Все величины предполагаются периодическими функциями горизонтальной координаты x с периодом L , где L — длина волны возмущений, соответствующая критическим числам Марангони, найденным в работе [16] для фиксированных значений других параметров.

На боковых границах расчетной области (см. Рис. 1) зададим условия периодичности:

ф (t, о, z ) = ф (t, L, z ) , ф (t,о, z ) = ф (t, l, z ) , v (t, о, z ) = v (t, L , z ) ,     6 (t, о, z ) = 6(t, L, z) .

Функции тока ф ( t , x , z ) и вихря скорости ф ( t , x , z ) характеризуют проекцию движения конечноамплитудных возмущений на плоскость O xz , вторая компонента скорости v ( t , x , z ) — проекцию на плоскость о yz или о xy . Положительная величина скорости определяет движение вглубь, а отрицательное значение — движение в противоположном направлении, то есть в перпендикулярном плоскости O xz .

Для пространственных спиральных периодических по y возмущений система принимает вид:

д ф       Г д ф д ф д ф д ф         д ф     „    д ф 1    /---д и          G r д 6

---+ M n I —--+--+ v ₀ ( z )--- + v ₀ ( z )--- | + V T a --- = А ф —-- д t       L д z д y д y д z          д y          д y J        д z         Mn д y

Аф + ф = о , ди       Г д ф ди дф ди          ди     „    дф 1    i---дф

---+ M n I —--+--+ v0 ( z )---+ v0 (z )----| + V T a ----= А и , д t        L д z д y д y д z          д y           д y J         д z a0      Г 5v 50

---+ M n I —-- а t        La z a y

5ш 50        50 5w    ,   5ш 1    1

--+ v о (z)---—----+ т о (z)----| = —А 0 , a y a z         a y   a y          a y J Pr а граничные условия на (z = ± 1 ) выглядят так:

ao      a u         ao _

V = 0, Ф = —--- ,    --- = 0,    --- = ⁺ Bi 0 .

a y       a z          a z

В выражениях (14)-(18) все величины предполагаются периодическими функциями горизонтальной координаты y с периодом L , где L — длина волны возмущений, соответствующая критическому числу Марангони для фиксированных значений других параметров. На боковых границах выполняются условия:

V (t, о, z) = V (t, L, z),     Ф (t, 0, z) = Ф (t, l, z ) , u (t ,0, z ) = u (t, L, z),     0( t ,0, z )=0 (t, L, z) .                                           (19)

Функции тока v ( t , y , z ) и вихря скорости ф ( t , y , z ) в этом случае выражаею проекцию движения конечноамплитудных возмущений на плоскость о yz , а компонента скорости u ( t , y , z ) — проекцию на плоскость о xz или о xy . Положительная величина скорости означает движение вглубь, а отрицательное значение — движение в противоположном направлении, то есть перпендикулярном плоскости о yz .

На основе систем уравнений (8)-(13) и (14)-(19) исследовалась структура конечно-амплитудных возмущений при фиксированных значениях Pr = 6,7 и Bi = 0,1 и различных значениях чисел Ta и Gr . Нелинейная двумерная задача решалась численно (методом сеток) [19]. В рамках двухполевого метода [20] использовалась явная конечно-разностная схема. Уравнение Пуассона для функции тока решалось методом последовательной верхней релаксации.

Расчеты проводились на сетке 100x401 при слабом вращении (число Ta варьировалось от 0 до 10). В условиях микрогравитации число Gr изменялось от 0 до 8. Для винтовых возмущений в качестве начальных возмущений функции тока и температуры бралась функция cos(2 п x/Lz )sin ² п z , для второй компоненты скорости — cos ( 2 п x/Lz ) cos² п z . При спиральных возмущениях в решении участвовали, соответственно, функции cos(2 п y/Lz )sin ² п z и cos(2 п y/Lz )cos 2 п z , удовлетворяющие граничным условиям.

В случае монотонной неустойчивости счет продолжался до достижения максимумами производных по времени в уравнениях (8), (10)-(11) и (14), (16)-(17) величины меньшей, чем 10-6. Для этого требовалось около 15 единиц модельного времени. При колебательной неустойчивости вычисления продолжались до установления регулярного режима (в течение ~20 единиц модельного времени).

Данные компьютерных экспериментов при постоянных параметрах Ta = 10, Gr = 1, kx = 1,5 6, Mn = 18 (Рис. 2) показывают, что стационарные конечно-амплитудные возмущения скорости и температуры возникают в случае монотонной неустойчивости при малых значениях числа Грасгофа. Нестационарные периодические возмущения формируются в случае колебательной неустойчивости. В качестве иллюстрации механизма поведения конечно-амплитудных возмущений использованы результаты расчетов на границах рассмотренных интервалов чисел Тейлора и Грасгофа. Вблизи минимумов нейтральных кривых возмущение температуры является системой пар чередующихся теплых и холодных пятен, расположенных вдоль оси x (Рис. 2а). Максимальная и минимальная температуры пятен одинаковы по абсолютной величине. Конечно-амплитудные возмущения образуют систему пространственных вихрей. Проекция движения, описанная функцией возмущения функции тока, около порога устойчивости представляет собой систему двух стационарных вращающихся против и по часовой стрелке вихрей (Рис. 2б). Одновременно вторая компонента скорости возмущения, имеющая отрицательное значение в середине слоя и положительное по краям, характеризует вращение стационарных вихрей против и по часовой стрелке соответственно (Рис. 2в).

При увеличении числа Марангони в два раза (см. Рис. 3) движение усложняется, максимальные значения возмущения температуры возрастают, холодное пятно в центре слоя смещается к верхней границе, а теплые пятна по бокам — к нижней границе слоя (Рис. 3 а ). Проекция движения, описанная возмущением функции тока, представляет собой систему чередующихся пар вихрей, экстремальные значения достигаются у верхней и нижней границ (Рис. 3 б ). Вторая компонента скорости дает систему из четырех вихрей (Рис. 3 в ), в центре слоя вращение происходит против часовой стрелки, по бокам — по часовой стрелке.

Рисунки 4–7 иллюстрируют расчеты, проведенные для случая колебательной неустойчивости при значениях параметров Ta = 10, Gr = 8, k_x = 0,5 3, Mn = 3 4 . В слабо вращающемся слое жидкости возникает периодически изменяющаяся картина конечно-амплитудных возмущений. Период составляет 1,34 единицы модельного (нормированного) времени и может быть разделен на четыре фазы движения.

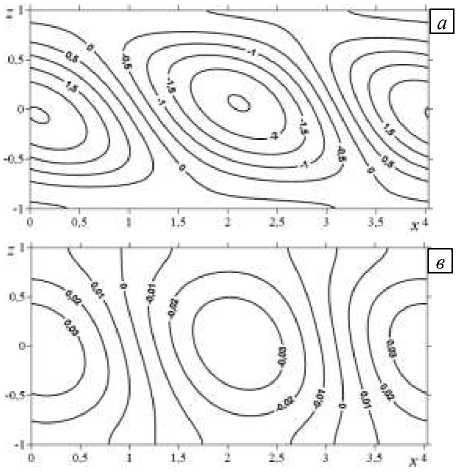
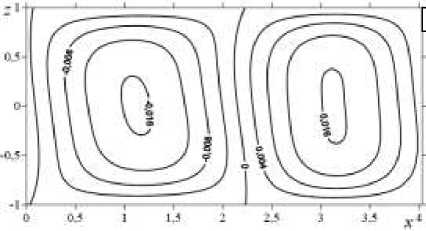
Рис. 2. Изолинии конечно-амплитудных возмущений температуры ( а ), функции тока ( б ) и второй компоненты скорости v ( в ) при Ta = 1 0, Gr = 1, k = 1, 56 и числе Марангони M n = 1 8

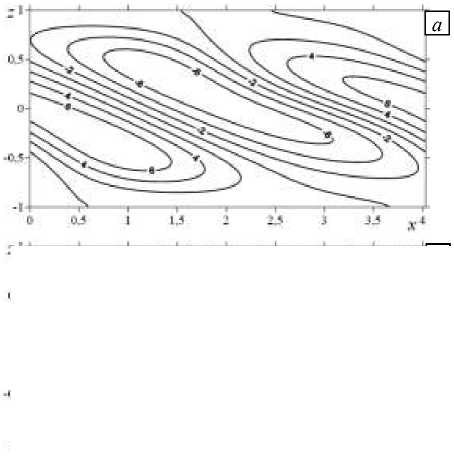
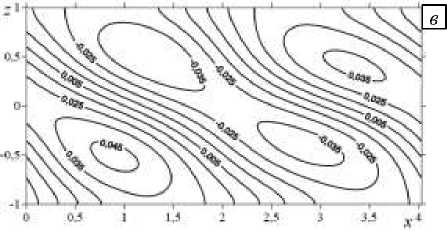
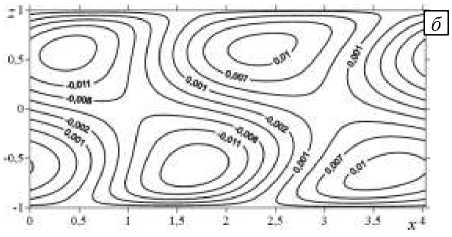
Рис. 3. Изолинии конечно-амплитудных возмущений температуры ( а ), функции тока ( б ) и второй компоненты скорости v ( в ) при Ta = 1 0, Gr = 1, k = 1, 56 и числе Марангони M n = 3 6

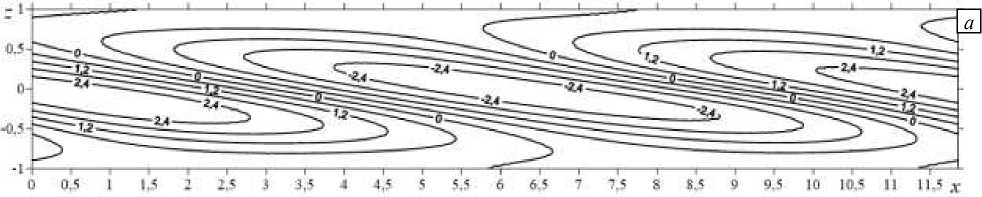
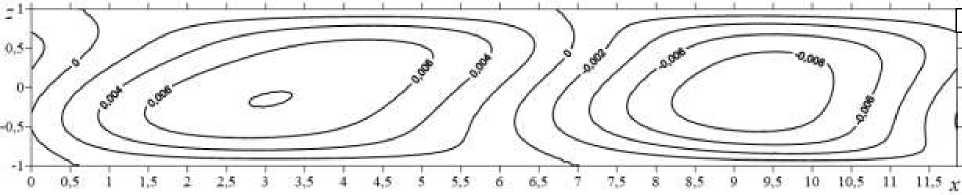
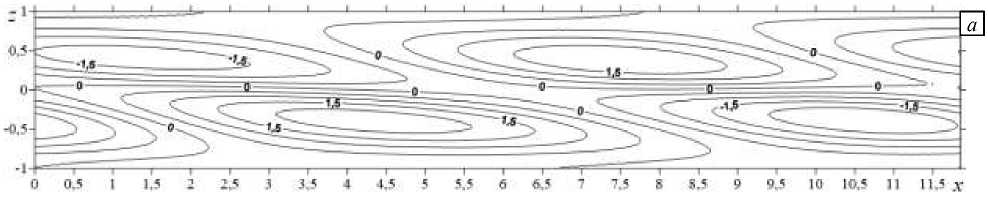
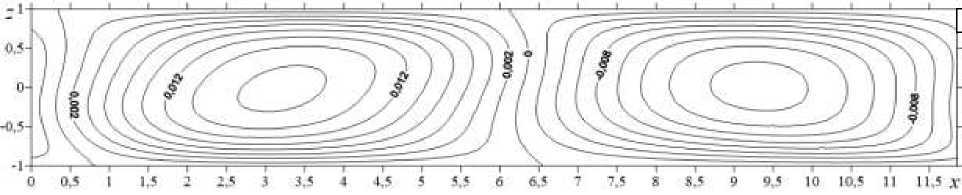
В 1-й фазе — вблизи минимумов нейтральных кривых, возмущение температуры выглядит как система чередующихся холодных и теплых пятен, располагающихся вдоль оси x (Рис. 4 a ). В плоскости O xz поперек слоя образуется повторяющаяся система из двух вихрей, вращающихся в противоположных направлениях: слева по часовой, справа против часовой стрелки (Рис. 4 б ). В плоскости O xy чередуются пары вихрей, вращающихся в одинаковых направлениях (Рис. 4 в ).

С течением времени жидкость движется вдоль верхней границы справа налево и в противоположном направлении вдоль нижней границы. Фаза 2 наступает через 0,28 единиц модельного времени (Рис. 5). Возле границ пары вихрей начинают разворачиваться поперек слоя. В центре слоя формируется теплое пятно, по бокам — холодные зоны.

9    9.5 IQ 10.5

а

Рис. 4. Фаза 1 колебательной неустойчивости: изолинии конечно-амплитудных возмущений температуры ( а ), функции тока ( б ) и второй компоненты скорости v ( в )

б

О.«*

в

9    9,5   10 10,5 11   11,5

Рис. 4. Продолжение

б

Рис. 5 . Фаза 2 колебательной неустойчивости: изолинии конечно-амплитудных возмущений температуры ( а ), функции тока ( б ) и второй компоненты скорости v ( в )

В 3-й фазе — через 0,29 единиц модельного времени (Рис. 6), пары вихрей продолжают разворачиваться поперек слоя, в центре образуется теплое пятно, на периферии — холодные зоны, в плоскостях O xz и O xy вихри имеют направления, противоположные характерным для фазы 1.

Фаза 4 наступает через 0,39 единиц модельного времени (Рис. 7). В центре слоя снова начинает формироваться холодное пятно. В плоскости O xz поперек слоя возникают повторяющиеся системы вихрей, вращающихся в одинаковых направлениях; в плоскости O xy вращение происходит по и против часовой стрелки, вихри локализуются в окрестностях границ. Далее, через 0,28 единиц модельного времени, снова наступает 1-я фаза.

Аналогично можно выделить 4 фазы движения в случае спиральных возмущений (Рис. 8–10). При параметрах T a = 1, Gr = 8, k = 0, 57, M n = 1 8 их период составляет 3,76 единицы модельного

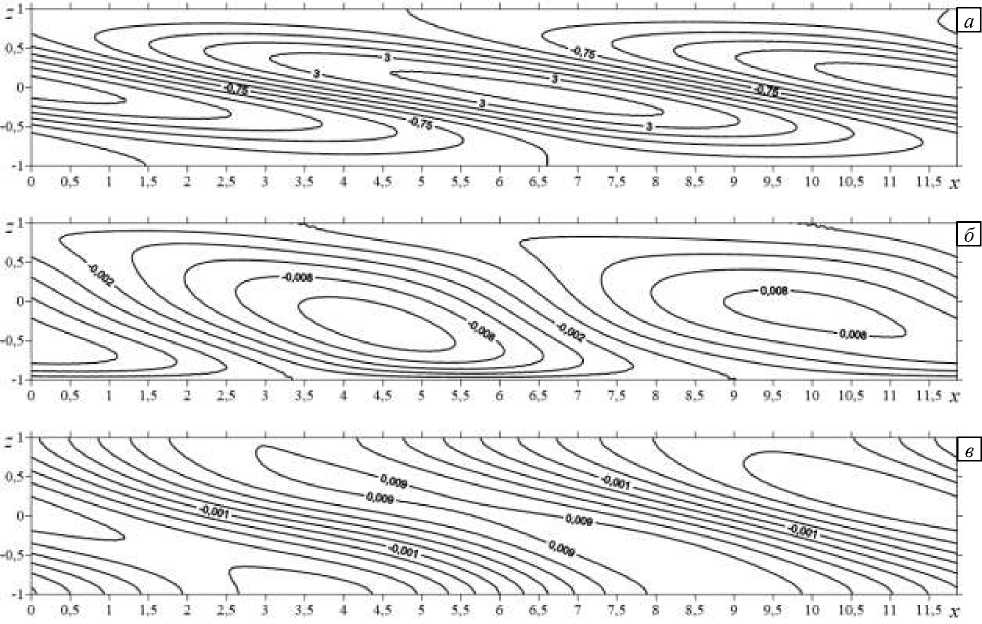
Рис. 6. Фаза 3 колебательной неустойчивости: изолинии конечно-амплитудных возмущений температуры ( а ), функции тока ( б ) и второй компоненты скорости v ( в )

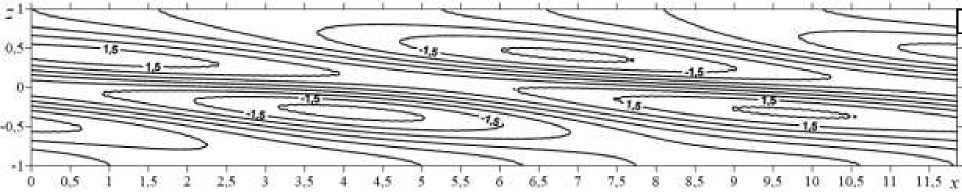
а

б

О-ОС*

■0.0»

■ООН

0.5-{

10 10.5 II   11.5.Г

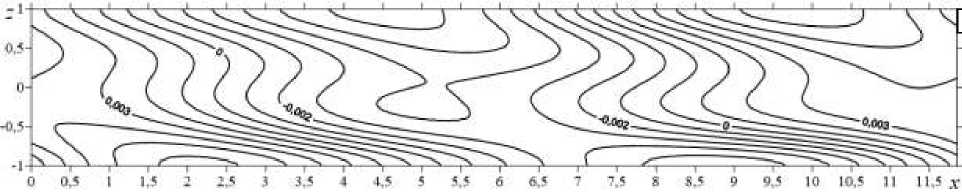
Рис. 7. Фаза 4 колебательной неустойчивости: изолинии конечно-амплитудных возмущений температуры ( а ), функции тока ( б ) и второй компоненты скорости v ( в )

Рис. 8. Изолинии конечно-амплитудных спиральных температурных возмущений в разных фазах : фаза 1 ( а ), фаза 2 ( б ), фаза 3 ( в ), фаза 4 ( г )

времени. Вблизи минимумов нейтральных кривых конечно-амплитудные возмущения температуры, имеющие вид чередующихся температурных пятен, с течением времени разворачиваются поперек слоя и одновременно продолжают двигаться вдоль границ (Рис. 8 а-г ).

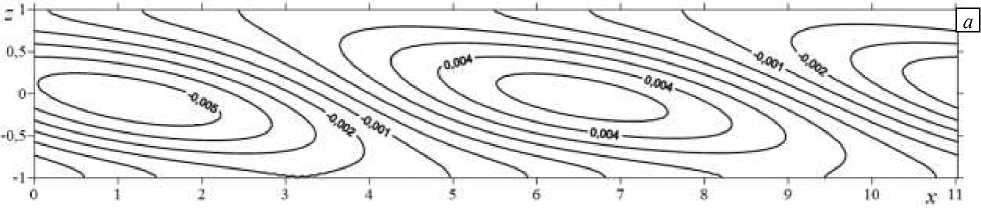
Функция тока, описывающая проекцию на плоскость о yz движения конечно-амплитудных возмущений, которые представляют собой системы вихрей, вращающихся по и против часовой стрелки (Рис. 9 а ). С течением времени вихри сдвигаются вдоль верхней и нижней границ (Рис. 9 б–г ). Аналогично периодически меняется вторая компонента скорости (Рис. 10).

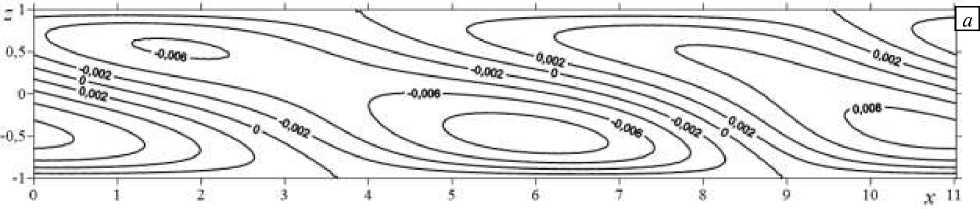
Рис. 9. Изолинии функции тока в случае спиральных возмущений: фаза 1 ( а ), фаза 2 ( б ), фаза 3 ( в ), фаза 4 ( г )

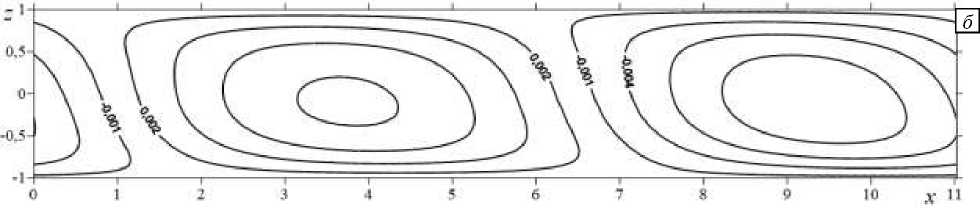
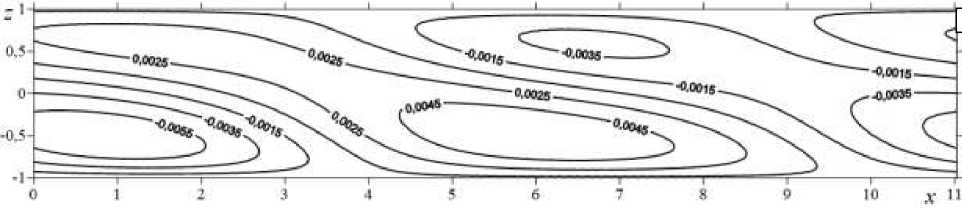
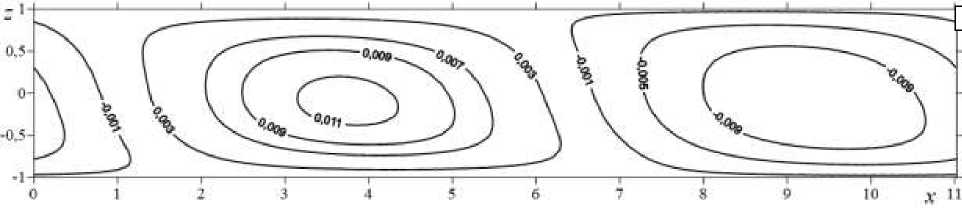
Рис. 9. Продолжение

oJO*

О,ОСИ

а

б

-слоем

OJO»'*

0,5

-0.00*

OJXH

в

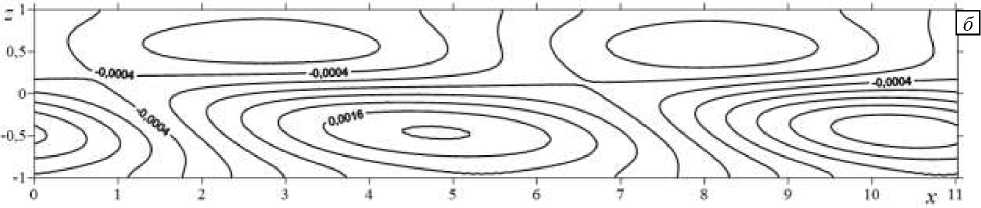
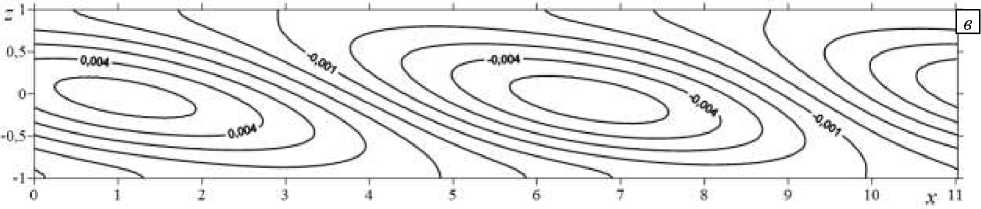
Рис. 10. Изолинии конечно-амплитудных возмущений компоненты скорости u в случае спиральных возмущений: фаза 1 ( а ), фаза 2 ( б ), фаза 3 ( в ), фаза 4 ( г )

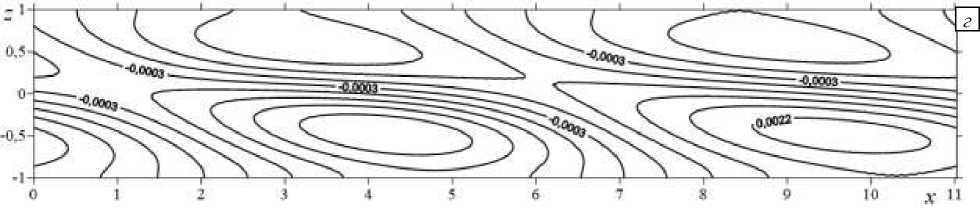
Рис. 10. Продолжение

4.    Заключение

Поведение конечно-амплитудных возмущений, возникающих во вращающемся слое жидкости при значениях числа Марангони выше критических, математическое описание которого сводится к нелинейной задаче, исследовано методом сеток. Рассмотрены случаи пространственных винтовых периодических по координате x возмущений в виде валов с осью, перпендикулярной оси O x , и пространственных спиральных периодических по y возмущений в виде валов с осью, параллельной оси O x . При монотонной линейной неустойчивости за порогом устойчивости формируются стационарные конечноамплитудные возмущения температуры и скорости, соответственно, в виде чередующихся холодных и теплых температурных пятен и систем вращающихся в противоположных направлениях пространственных вихрей. Для колебательной неустойчивости характерны нестационарные периодические возмущения в виде пространственных вихрей и температурных пятен, которые с течением времени разворачиваются поперек слоя и двигаются вдоль его границ. При увеличении числа Марангони максимальные значения температуры возрастают, движение усложняется, экстремальные значения скорости достигаются вблизи верхней и нижней границ.