Численное моделирование локально нагруженных через шпангоуты трехслойных композитных цилиндрических оболочек
Автор: Сухомлинов Л.Г., Шиврин М.В.
Статья в выпуске: 3, 2021 года.
Бесплатный доступ
Рассматривается композитная (на основе стеклоткани) конструкция в виде подкрепленной шпангоутами трехслойной с пенопластовым заполнителем цилиндрической оболочки, находящейся под действием локальных нагрузок, приложенных к шпангоутам. Излагается методика получения (с подтвержденной достоверностью) численного решения задачи о напряженно-деформированном состоянии подобного типа конструкций с применением двух альтернативных вычислительных моделей, одна из которых основана на методе численного интегрирования, а другая на методе конечных элементов. Разработка первой модели осуществляется с принятием расчетной схемы, при которой шпангоуты рассматриваются как короткие цилиндрические оболочки, подчиняющиеся гипотезе единой нормали, а соединенные с ними трехслойные участки рассматриваются в рамках теории трехслойных с легким заполнителем оболочек, основанной на гипотезе ломаной линии и предположении о несжимаемости заполнителя по толщине. При этом соответствующая задача расчета формулируется в виде систем алгебраических и дифференциальных (в частных производных) уравнений для каждого из введенных в рассмотрение оболочечных участков, которые дополняются кинематическими и силовыми условиями на их стыках, а также граничными условиями на левом и правом торце конструкции. С использованием процедуры разложения параметров напряженно-деформированного состояния и приложенных нагрузок в ряды Фурье по окружной координате решение поставленной задачи при каждом номере гармоники сводится к решению совокупности краевых задач для систем из 8 и 12 линейных обыкновенных дифференциальных уравнений первого порядка, связанных условиями на указанных стыках. Алгоритм решения строится с использованием процедуры численного интегрирования в варианте ортогональной прогонки в сочетании с процедурой метода перемещений (для удовлетворения условий на стыках). Заявленная конечно-элементная модель строится в рамках программного комплекса ABAQUS с использованием оболочечных элементов типа S4 (применительно к композитным слоям) и объемных элементов типа C3D20 (применительно к шпангоутам и заполнителю). Образованная модель при задании заведомо завышенных значений соответствующих модулей упругости обладает возможностью реализовать ситуацию, близкую к выполнению набора гипотез, принятых при построении первой модели. Зафиксировав в такой ситуации согласованность результатов расчетов на основе построенных отмеченным образом альтернативных вычислительных моделей и тем самым подтвердив достоверность получаемого численного решения, далее осуществляли переход к расчету с использованием реальных значений упомянутых модулей и анализу их влияния на напряженно-деформированное состояние исследуемой трехслойной оболочки. Представленный пример расчета трехслойной конструкции, один из шпангоутов которой находится под действием двух локальных осевых нагрузок, демонстрирует возможности принятого способа моделирования.
Подкрепленная шпангоутами трехслойная с легким заполнителем цилиндрическая оболочка, локальные нагрузки, метод конечных элементов, метод численного интегрирования
Короткий адрес: https://sciup.org/146282361
IDR: 146282361 | УДК: 539.3 | DOI: 10.15593/perm.mech/2021.3.15
Текст научной статьи Численное моделирование локально нагруженных через шпангоуты трехслойных композитных цилиндрических оболочек
ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2021PNRPU MECHANICS BULLETIN
Все большее применение в различных отраслях экономики находят конструкции типа усиленных шпангоутами композитных цилиндрических оболочек. Часть из них выполняется по схеме трехслойных (с пенопластовым заполнителем) оболочек, производимых путем намотки на цилиндрическую оправку стеклоткани, пропитанной полимерным связующим (с последующей термообработкой). Шпангоуты в процессе такой намотки формируются в виде локальных кольцевых утолщений. Полученный в указанном технологическом процессе материал несущих слоев оболочки (стеклопластик) обладает ортотропией свойств и упруго реагирует на приложенную нагрузку. Пенопласт, заполняющий пространство между несущими слоями, относится к классу легких заполнителей и имеет почти в 1000 раз меньшее значение модуля Юнга, чем у стеклопластика. Пример такого типа оболочки с четырьмя шпангоутами 1, 3, 5, 7 и тремя оболочечными секциями 2, 4, 6, имеющими единую внутреннюю поверхность радиусом R, схематично представлен на рис. 1. Подоб- ные оболочки могут быть достаточно протяженными и с самым разнообразным количеством шпангоутов. В условиях эксплуатации оболочки рассматриваемого типа могут подвергаться воздействию значительных по величине локальных нагрузок, прикладываемых к шпангоутам. Отсюда запрос на расчетные методы, позволяющие адекватно оценивать напряженно-деформированное состояние такого типа оболочек в условиях локального нагружения.
Среди развитых к настоящему времени аналитических подходов к расчету локально нагруженных оболочек можно выделить подходы, основанные на применении двойных и одинарных рядов Фурье, на сочетании одинарных рядов Фурье и одномерных преобразований Фурье, на применении двумерных преобразований Фурье, на применении преобразований Лапласа, а также на применении различных вариантов асимптотических методов [1–6]. При этом лишь несколько из них [7–9] ориентированы на расчет локально нагруженных через шпангоуты композитных цилиндрических оболочек. Шпангоуты в этих подходах рассматриваются по схеме кольца с недеформируемым поперечным сечением, а оболочечные секции рассматриваются на основе соотношений теории оболочек с введением упрощений, связанных с принятием полубезмоментной гипотезы В.З. Власова [10]. Это означает, что представленные в работах [7–9] приближенные аналитические решения, игнорирующие изгибные деформации (и изгибающие моменты) в меридиональном направлении, не могут быть использованы для оценки уровня напряжений в зонах стыков оболочечных секций с нагруженными шпангоутами, где изгибные эффекты играют определяющую роль. Если обратиться к публикациям, посвященным расчету трехслойных (с заполнителем) оболочек численными методами (в большинстве случаев это конечно-элементные решения [11–16]), то можно отметить их направленность на разработку моделей конечных элементов, способных учитывать те или иные особенности деформирования слоев в рамках трехслойного пакета (в частности, сжимаемость заполнителя). Приводятся соответствующие примеры, демонстрирующие эффективность расчетных моделей с использованием таких элементов. Однако среди этих примеров не обнаруживаются решения, относящиеся к обозначенным задачам о локально нагруженных через шпангоуты трехслойных оболочках.
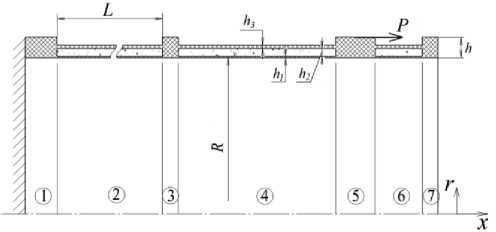
Рис. 1. Схема композитной трехслойной с пенопластовым заполнителем цилиндрической оболочки, усиленной шпангоутами
Fig. 1. A scheme of a sandwich cylindrical shell with a foam filler, reinforced with frames
В настоящее время расчеты подобного типа конструкций в проектных организациях выполняются, как правило, с использованием коммерческих программных конечно-элементных комплексов. Важным при этом является вопрос о достоверности получаемого конечноэлементного решения в смысле его близости к соответствующему точному решению поставленной задачи во всех точках оболочки, включая зоны стыков с нагруженными шпангоутами. Учитывая значительную протяженность обсуждаемого типа оболочек и локальный характер приложенных нагрузок, подтверждение надежности расчетных результатов на основе процедуры варьирования расчетной сеткой представляется проблематичным [17]. Эффективным в этом плане представляется способ, при котором поставленная задача о локальном нагружении решается двумя альтернативными методами. При этом вывод о достоверности получаемо- го решения делается по факту согласованности результатов расчетов с использованием двух указанных методов. Такой способ подтверждения достоверности получаемого решения применительно к задачам о напряженно-деформированном состоянии изотропных и ортотропных оболочек при действии локально приложенных нормальных поверхностных нагрузок продемонстрирован в работах [18, 19]. В настоящей статье подобный способ применяется при конечно-элементном решении обозначенного типа задачи о локальном нагружении с использованием программного комплекса ABAQUS.
1. Описание расчетной методики
Рассматриваем тонкую трехслойную с легким заполнителем оболочку типа, представленного на рис. 1. Две альтернативные вычислительные модели строим параллельно, учитывая возможности принимаемых к реализации численных подходов. Альтернативную конечно-элементному (КЭ) подходу вычислительную модель будем строить, ориентируясь на метод численного интегрирования (ЧИ) в варианте ортогональной прогонки С.К. Годунова [20], принимая во внимание, что этот метод показал высокую эффективность при решении широких классов задач статики оболочек вращения [21, 22]. Остается решить вопрос, какую из возможных расчетных схем трехслойной оболочки допустимо принять в рассматриваемом случае легкого заполнителя. Представленные в литературе [23–29] материалы с анализом различных теорий трехслойных оболочек дают основание полагать, что в ситуациях, когда локальные нагрузки действуют только на шпангоуты (и тем самым предотвращаются локальные смятия заполнителя), расчет напряженно-деформированного состояния оболочек рассматриваемого типа допустимо проводить в рамках соотношений теории оболочек, построенной на гипотезе ломаной линии в сочетании с предположением о несжимаемости заполнителя по толщине [30]. Шпангоуты (имеющие малую по сравнению с радиусом оболочки толщину) будем рассматривать по схеме (короткой) цилиндрической оболочки, подчиняющейся гипотезам Кирхгофа–Лява [31]. Решение задачи о локальном нагружении объекта в виде последовательно соединенных друг с другом коротких цилиндрических участков и трехслойных секций, подчиняющихся указанному набору гипотез, будем считать опорным. Заявленную конечно-элементную модель с использованием комплекса ABAQUS будем строить таким образом, чтобы при задании заведомо завышенных значений соответствующих модулей упругости можно было реализовать ситуацию, близкую к выполнению указанного набора гипотез. Зафиксировав согласованность результатов расчетов на основе построенных отмеченным образом альтернативных вычислительных моделей и тем самым подтвердив достоверность получаемого численного решения, далее можно перейти к КЭ-расчету с исполь- зованием реальных значений упомянутых модулей и анализу их влияния на напряженно-деформированное состояние исследуемой трехслойной оболочки.
2. Постановка задачи для двух типов оболочек
Переходя к построению обсуждаемой ЧИ-модели (основанной на методе численного интегрирования), условимся называть входящие в ее расчетную схему оболочечные участки, подчиняющиеся гипотезам Кирх-гофа–Лява, оболочками первого типа, а трехслойные участки - оболочками второго типа. Исходим из того, что расчетная ЧИ-модель включает N оболочек первого типа и N -1 оболочек второго типа, занумерованных последовательно от 1 до 2 N -1. Пусть x , ф, r - цилиндрические координаты (см. рис. 1), где осевая координата x отсчитывается от левого края каждой из введенных в рассмотрение оболочек. Вводим также систему координат x , ф, z , где координата z отсчитывается от внутренней поверхности каждой из оболочек в радиальном направлении. Отмечаем, что принятый для оболочки второго типа набор гипотез фактически означает, что каждый из ее несущих слоев рассматривается по схеме оболочки, для которой справедливы гипотезы Кирхго-фа–Лява. Заполнитель сопротивляется лишь поперечным сдвигам. При этом его сдвиговые деформации постоянны по толщине. Предполагаемая несжимаемость заполнителя означает, что нормальные перемещения постоянны по толщине всего трехслойного пакета и равны соответствующему перемещению w поверхности приведения. Из сказанного следует, что соотношения, описывающие напряженно-деформированное состояние оболочек второго типа, можно сформулировать по аналогии с тем, как это сделано в классическом варианте теории оболочек [31]. При записи таких соотношений будем использовать обозначения, принятые в работе [21].
Итак, пусть 1 и 3 - номера нижнего и верхнего несущих слоев обсуждаемого типа оболочки, а 2 - номер слоя заполнителя. Толщины указанных слоев будем обозначать как h 1 , h 2, h 3. Пусть z 0 = 0 - значение координаты z внутренней поверхности (поверхности приведения) трехслойной оболочки. Введем в рассмотрение параметры z i ( i = 1, 2, 3), вычисляемые по схеме z i = z i -1 + h i . Тогда принадлежность точки с координатой z i -му слою ( i = 1, 2, 3) будет описываться неравенством z i .1 < z < z i .
С учетом сделанных пояснений указанные выше соотношения для рассматриваемой оболочки второго типа могут быть представлены в следующем виде.
-
1) Геометрические соотношения
Uj = uj + z 9, Vj = vj + z 9 j , Wj = w, 91 = - w\ 9 j = - w * + V (R ;
E i i = ( uJ )', E h = ( v j ) ‘ + w/R , E j = ( v ) ' + ( u j ) ' ;
K i 1 = 9 ' , K 22 = (9/) ' , K i j = 9 ; + ( V)!R ;
eJi (z) = E1 + zKij1, j j jj j j e22 (z ) = E22 + zK22 , e12 (z ) = e12 + 2zK12 ;
4 = (u 3 — u 1)/ h , е 2з = ( v 3 - v )/ h ;
(j = 1, 3), G-.)^^
1 dCO R дф '
Здесь и далее для обозначения параметров, относящихся к осевому направлению x и окружному направлению φ, используются нижние индексы 1 и 2. Верхний индекс введен для обозначения номера слоя. Параметры u , v , w -представляют собой перемещения точки, относящейся к поверхности приведения, а U , V , W - перемещения точек, отличающихся от указанной точки ненулевой координатой z. Параметры 9 1, 9 2 представляют собой углы поворотов; параметры E 11 , E 22, E 12, K п, K 22, K 12 -относительные удлинения, сдвиг, изменения кривизн и кручение (относящиеся к поверхности приведения); параметры 8ц( z ), 822( z ), 812( z ) - относительные удлинения и сдвиг в точках с ненулевой координатой z ; параметры 813, 823 - поперечные сдвиги в заполнителе.
-
2) Физические соотношения (соотношения упругости для случая ортотропных слоев)
Ej
° ii = " "j ™( eii + v21е22 ) (1<—- 2);
1 - vn v 2 i
Qn = G1jl е12 , ( E 1 j V21 = E2 V12 ) , ( j = 1 , 3);
2 C2P2 2 =C2^2
° 13 G 13e13 , ° 23 G 23e23 ’
T = B 1 E i 1 + B i j E j + A 1 K i 1 + A i K.... (1 ^ 2);
S = BjEj + 2 AjKj;
M 1i = Ah Eh + Ah E j + Dh Ki i + D h K j (1^2);
H j = A 3^3 Eh + 2 D j Kh;
B 1 J , = E i h j , B j = V 21 B j , E i = E i /(1 - v j v 22, ) (1 ^ 2);
Ai i = E i (z j - Zj 2 - i )/2, A i j = v 2, A ii (1^2);
D ii = E i (z j - z 3 - i )/3, D i i = V 21 D ii (1^2);
B 33 = G , j h j , A 33 = Gh ( z 2 - zj )/2, D^ 3 = G , j ( z 3 - zj . )/3.
Здесь T 11 , T 22, S и M 11 , M 22, H - соответствующие усилия и моменты в несущих слоях оболочки; B lm , A lm , D lm -жесткостные характеристики несущих слоев оболочки относительно выбранной поверхности приведения.
-
3) Уравнения равновесия
j j •• „1^1 „3е3 _2 ei „_2 e3
( T ii ) + ( S ) + q i О j + q i О j + 0 13 О j - $ 13 ° j = 0;
( Sj ) ' + ( T 2 i ) • + [( M j ) • + 2( Hj И / R + q 2 8 j +
+ q 2 ° 3 + ° 23 ° J -- ° 23 ° j = 0;
Q ii + Q 2 ' 2 - ( X T 2 i ) / R + q -- = °, ( J = i, 3);
j
M} 1+ H • - Qn = °, M •+ H '- Q.. = °,
11 11 22 22
где мп = £м/„ м22 = £м22, н = £H.
j j j
Параметры q 1, q 2, q z , входящие в эти уравнения, представляют собой интенсивности распределенных поверхностных нагрузок; параметры о .3, а23 - сдвиговые напряжения в заполнителе; 5 j i - символ Кронекера.
4) Граничные условия
3. Вопросы реализации расчетной ЧИ-модели
Кинематические условия на торцах оболочки второго типа формулируются в виде uj = u*j, vj = v*j, w = w*, 01 = 01*, а статические в виде
T 1 = T', SJ + 2 Hp = T !' Qu + H •= Q„ M„ = M*vv.
При этом j = 1, 3. Звездочкой в правых частях указанных равенств отмечены заданные на торцах значения соответствующих факторов.
Система соотношений, описывающая напряженно-деформированное состояние оболочки первого типа, получается на основе сформулированной выше системы путем исключения из ее записи соотношений и параметров, относящихся к третьему и второму слою. Исключается также излишний в данном случае верхний индекс «1» у соответствующих параметров, который указывает на номер несущего слоя.
Переходя к формулировке строящейся ЧИ-модели в целом, укажем, что она заключается в записи для каждой из N оболочек первого типа и каждой из N–1 оболочек второго типа соответствующих соотношений из представленных двух типов формулировок. При этом вместо указанных выше граничных условий, ориентированных на случай отдельной оболочки, необходимо сформулировать условия на стыках оболочек, входящих в обсуждаемую расчетную модель. Замечая, что схема ломаной линии в случае оболочки второго типа на стыке с оболочкой первого типа переходит в схему прямой линии, приходим к записи кинематических и статических условий на каждом из таких стыков в виде u = U, u3 = U, v1 = v, v3 = v, w = W, 0=0; (1)
T 1 = T 1 + T 3 , S + 2 HR = s 1 + 2 H 7 R + S 3 + 2 H3 /R ; Q 11 + H• = Q 11 + ( н *) • + ( н 3y, м 11 = м 11 + м 131 .
(Здесь и далее «волной» отмечаются параметры, относящиеся к оболочке первого типа). К этим условиям необходимо еще добавить условия на левом и правом торце оболочек с номерами 1 и 2 N –1. В случае схемы, представленной на рис. 1, имеются в виду условия жесткого закрепления на левом торце:
U = 0, v = 0, W = 0, 0 = 0(3)
и условия свободного края на правом торце :
T. = 0, S + 2HR = 0, Q. + He= 0, ми = 0.(4)
11 111
Для решения поставленной задачи представим параметры напряженно -деформированного состояния и приложенных нагрузок в виде рядов Фурье по окружной координате φ. Подставляя указанные Фурье разложения в описанные выше соотношения поставленной задачи, для каждого фиксированного номера гармоники n получим аналоги этих соотношений, содержащие амплитудные значения исходных параметров. (Индекс “ n ” у этих значений для простоты указывать не будем.) Из амплитуд кинематических параметров, входящих в формулировку граничных условий, образуем столбец обобщенных перемещений вида [ t ] = ( u 1, u 3, v 1, v 3, w , 0! ) T применительно к оболочке второго типа и вида [t ] = ( U , v , W , 01 )T применительно к оболочке первого типа. В том же порядке из амплитуд параметров, входящих в статические граничные условия, образуем соответствующие столбцы обобщенных усилий [ p ] и [ p ], состоящие из шести и четырех элементов. Из этих столбцов формируем столбцы [ у ] и [ у ] вида
Г [ р Л Г [ p Г
[ у ] = и [ у ] = .
L e t ] J L e t ] J
С использованием введенных в рассмотрение параметров у ( i = 1, 2,..., 12) и у ( i =1, 2,..., 8) набор входящих в постановку рассматриваемой задачи соотношений для каждого номера гармоники n сводится к совокупности краевых задач для систем из 12 и 8 линейных обыкновенных дифференциальных уравнений (по координате x ) первого порядка вида
{ Л } [ у 1 = { S } [ у ] + [ 6 ] (5)
для каждой из оболочек второго типа и вида;
{ ^ } [ у 1 = { s } [ у ] + [ b ] (6)
для каждой из оболочек первого типа. Столбцы [ b ] и [ b ] указанных систем включают амплитудные значения параметров приложенных поверхностных нагрузок.
Введем для левого и правого торца каждой из оболочек расчетной модели номера 1 и 2 . Пусть i - номер оболочки второго типа ( i =2, 4,..., 2 N -2), стыкуемой своим левым и правым торцами с оболочками первого типа, имеющими номера i -1 и i +1. Тогда кинематические условия (1) на стыках оболочек первого и второго типов можно представить в виде
[ t ] 1- < = { С }Й2- ' '- 1 , [ t ] 2, / = { C } [ Z ]1’ , + 1 (i = 2,4,...,2 N - 2), (7) где { С } - матрица размером 6x4, ненулевые элементы которой имеют вид
С = С = С = С = С = С =1
11 ^21 ^32 ^42 ^53 ^64 1.
Аналогичную матричную форму можно придать и силовым условиям (2) на тех же стыках, а именно
[ Р ]2 ’ i - 1 = { C } T [ p ] •• ' ,[ P ]11 / + 1 = { C } T [ p ]2, z ( i = 2,4,...,2 N - 2). (8)
К этим записям необходимо добавить упомянутые выше условия жесткого закрепления и свободного края на левом и правом торце обсуждаемой расчетной модели, которые представимы в виде
[ t T* = 0, [ p ]2,2 N - 1 = 0. (9)
Теперь переходим к обсуждению этапа, когда на основе обозначенного метода численного интегрирования в варианте ортогональной прогонки необходимо осуществить решение систем дифференциальных уравнений вида (6) для оболочек с номерами (1, 3,., 2 N -1) и вида (5) для оболочек с номерами (2, 4,., 2 N-2), удовлетворив при этом условиям вида (7)–(9) на торцах этих оболочек. Соответствующая программная реализация выполняется следующим образом.
За основу берем представленную в работе [21] процедуру ортогональной прогонки с численным интегрированием по методу Кутта–Мерсона, ориентированную на решение краевой задачи для системы из 2 m линейных дифференциальных уравнений первого порядка при заданных m условиях на каждом из краев. При этом используем версию этой процедуры, настроенную на задание краевых условий в перемещениях. Далее реализуем алгоритм решения поставленной задачи на основе метода перемещений. Исходим из того, что для s -й оболочки расчетной модели ( s =1,2,..., 2 N -1) в силу линейности соответствующей системы уравнений (5) или (6) имеет место линейная связь между обобщенными перемещениями и обобщенными усилиями на ее торцах с номерами 1 и 2, которая представима в матричном виде:
■ [ Р ] 1 5 =| { k 11} { k 12} 1 5 Г 1 t ]1 1 5 Г1 g ]1
.[ p ] 2 J l { k 2‘) { k 22} J L [ t ] 2 1 [ [ g ] 2
( p^p , kp^k , t ^ t , g ^.g ).
Вычисление значений, входящих в запись (10), элементов матриц { K } и { K } , составленных из подматриц { к ав } и { к ав } , а также элементов подстолбцов
[ g ] 1 ,[ g ]2,[ g ] 1 ,[ g ]2 осуществляем, решая с использованием указанной выше процедуры ортогональной прогонки ряд краевых задач для систем (5) и (6) с заданными граничными условиями в перемещениях. Выполняемые при этом действия состоят в следующем.
Принимаем во внимание, что при [t]1 = [t]2 = 0 из вы ражения (10) следуют равенства [g]1 = [p]1, [g]2 = [p]2.
Это означает, что для определения значений элементов столбцов [g]1 и [g]2 необходимо одну из упомянутого ряда краевых задач для s-й оболочки (s =1,2,., 2N-1) решить при нулевых граничных условиях в перемещениях. Определив в результате такого решения обобщенные усилия [p]1 и [p]2 на торцах этой оболочки, мы тем самым находим искомые значения элементов столбцов [g]1 и [g]2 . Остальные решения по обсуждаемому ряду краевых задач осуществляем применительно к системам (5) и (6) с нулевыми столбцами [b] и [b], что соответствует ситуации нулевых значений, приложенных к s-й оболочке поверхностных нагрузок и нулевых значений элементов столбцов [g]1 и [g]2 в записи (10). В такой ситуации из записи (10) следует, что если в столбце, составленном из подстолбцов [t]1 и [t]2, обнулить все элементы кроме i-го, который в свою очередь принять равным единице, то i-й столбец матрицы {K} окажется равным столбцу, составленному из подстолбцов [p]1 и [p]2 . Учитывая сказанное, находим значения элементов столбцов матрицы {K} каждой оболочки на основе определения обобщенных усилий [p]1, [p]2 на ее торцах путем решения последовательности соответствующих краевых задач в условиях, когда одна из компонент обобщенных перемещений на краях оболочки равна единице, а остальные равны нулю.
Итак, считаем, что для каждой из оболочек числовые значения элементов, входящих в матричную зависимость (10), установлены. Выражая с использованием этой зависимости столбцы обобщенных усилий на торцах 1 и 2 каждой оболочки через соответствующие столбцы обобщенных перемещений и подставляя полученные связи в равенства (8) и (9), приходим к матричным равенствам, устанавливающим связи между обобщенными перемещениями [t]1, [t]2, [t ]1, [t ]2 торцов оболочек с соответствующими номерами. Подставляя в эти равенства выражения (7), окончательно получаем разрешающую систему линейных алгебраических уравнений относительно искомых значений элементов столбцов [t]1,z,[t]2,z (i =1, 3,..., 2N-1), представляющих собой обобщенные перемещения на торцах оболочек первого типа. После решения этой системы (по методу Гаусса) определяем с использованием равенств (7) обобщенные перемещения на торцах оболочек второго типа. Далее с использованием процедуры ортогональной прогонки осуществляем решение систем (5) и (6) для каждой из входящих в расчетную модель оболочек второго и первого типа при уже найденных значениях торцевых перемещений этих оболочек. На основе устанавливаемых при этом значений параметров УАx), У' (x) (i =1, 2,..., 12) и yz(x), yz' (x) (i =1, 2,..., 8) вычисляем, используя представленные выше геометрические и физические соотношения, амплитудные значения параметров напряженно-деформированного состоя- ния (в заданных точках x), относящиеся к текущему номеру гармоники n. Окончательные результаты по каждому из искомых параметров напряженно-деформированного состояния (как функций координат x, φ) получаем путем суммирования соответствующих гармонических составляющих в цикле по указанным номерам n.
4. Описание исследуемой конструкции
Остановимся теперь на описании геометрических и физико-механических характеристик оболочечной конструкции (см. рис. 1), расчет которой предстоит выполнить с применением ЧИ- и КЭ-моделей. Длины L (мм) ее участков 1 , 2 , 3 , 4 , 5 , 6 , 7 оцениваются величинами 200, 2000, 100, 1000, 250, 300, 100 соответственно. Радиус R = 1000 мм. Толщины слоев участков с номерами 2 , 4 , 6 заданы в виде h 1 =4 мм, h 2 = 56 мм, h 3 = 10 мм. Толщины участков с номерами 1 , 3 , 5 , 7 одинаковы и имеют величину h = 120 мм. Несущие слои трехслойных участков 2 , 4 , 6 и шпангоуты 1 , 3 , 5 , 7 выполнены из стеклопластика с характеристиками: E i = 1,8 - 10 4 МПа, E 2 = 2,3 - 10 4 МПа, G 12 = 0,42 - 10 4 МПа, ν21 = 0,13. Расположенный между несущими слоями изотропный пенопластовый заполнитель имеет характеристики: E = 22 МПа; ν = 0,2; G = 9,2 МПа. К поверхности шпангоута 5 приложены две одинаковые локальные осевые нагрузки величиной P = 106 Н. Угловой размер зон (в окружном направлении), вдоль которых (равномерно) распределены нагрузки P , имеет величину 2α0 = 0,1. Считаем, что векторы сил P расположены в осевом сечении рассматриваемой конструкции, включающем точки с координатами φ = 0 и φ = π. Так что указанные зоны распределения нагрузок P могут быть описаны неравенствами (–α0 ≤ φ ≤ α0) и (π – α0 ≤ φ ≤ π + α0).
Принимаем во внимание, что для функции f(φ), которая равна постоянной величине q внутри этих зон и равна нулю вне их, разложение в ряд Фурье записывается в виде to f (ф) = a0 -^'n cos ( 2 n Ф) , (11)
n = 1
где
a6 = 2qa0 /n , an = 2qsin(2na0)/ (nn). (12)
5. Реализация расчетной КЭ-модели в рамках комплекса ABAQUS
Обращаем также внимание на то, что при построении описанной ЧИ-модели в качестве поверхности приведения выбрана внутренняя поверхность (радиусом R) рассматриваемой конструкции; в схему нагружения шпангоута 5 наряду с силами P следует дополнительно включить два локальных момента величиной M = Ph = 1,2-108 Н-мм. При включении каждой из пар локальных нагрузок P и M в расчетную ЧИ-модель будем сводить их к статически эквивалентной системе действующих на оболочку 5 поверхностных нагрузок с интенсивностями qx и qz (в осевом и нормальном направлениях), которые распределены по зонам приложе- ния нагрузок P, имеющих размеры 2α0 и L (в окружном и осевом направлениях). Вычисление значений параметров qx и qz в указанных зонах проводится с использованием выражений qx = P/(2a0RL), qz =-M(x - 0,5L)/(2a0RJ), J = L3/12.
Разложение локально действующих силовых факторов q x и q z в ряды Фурье по координате φ осуществляется по схеме (11)–(12), где в одном случае следует принять q = qx , а в другом случае q = qz .
Отличительными особенностями описанной трехслойной конструкции являются ее существенная протяженность, наличие четырех шпангоутов и существенное различие в толщинах ее несущих слоев. В связи с этим укажем, что выполненные в работах [9, 32, 33] экспериментальные и расчетные исследования касались лишь трехслойных оболочек, несущие слои которых имеют одинаковую толщину и подкреплены двумя одинаковыми торцевыми шпангоутами.
Построение расчетной КЭ-модели для рассматриваемой конструкции (см. рис. 1) в рамках программного комплекса ABAQUS проводилось с применением элементов типа S4 и C3D20. Укажем, что элемент S4 представляет собой четырехугольный (четырехузловой) изопараметрический оболочечный элемент с шестью степенями свободы в узле (три перемещения и три поворота), построенный в рамках теории оболочек, учитывающей поперечные сдвиги по схеме прямой линии. Поэтому при создании с помощью такого элемента вычислительных моделей в случае ортотропных оболочек требуется дополнительно задавать модули поперечного сдвига G 13, G 23 материала оболочки. Элемент C3D20 представляет собой объемный двадцатиузловой шестигранный (изопараметрический с квадратичной функцией формы) элемент, позволяющий строить вычислительные модели применительно к упругим ортотропным телам.
При построении обозначенной КЭ-модели шпангоуты и заполнитель представлялись ансамблями объемных элементов, а несущие слои – ансамблями оболочечных элементов. В процессе такого построения пришлось учитывать, что узлы ансамбля объемных элементов шпангоута, принадлежащие его торцу, стыкуемому с оболочкой, имеют по три степени свободы (в виде перемещений в направлениях координатных осей) в отличие от стыкуемых с указанным торцом узлов оболочечных элементов несущих слоев, которые помимо перемещений имеют поворотные степени свободы. Необходимо было обеспечить соответствие поворота торца дискретной модели шпангоута повороту торцов дискретных моделей несущих слоев стыкуемой с этим шпангоутом трехслойной оболочки. Это кинема- тическое условие было реализовано таким образом, что на все узлы, принадлежащие торцу шпангоута и стыкуемых с ним оболочечных элементов, средствами комплекса ABAQUS накладывались кинематические связи, соответствующие принятию гипотезы прямой линии.
Расчетные исследования проводились с использованием трех вариантов такой КЭ-модели: КЭ-1, КЭ-2, КЭ-3. Модель КЭ-1 строилась таким образом, чтобы она обладала возможностью соответствовать предположениям, на которых основана ЧИ-модель. Условие несжимаемости заполнителя по толщине при этом обеспечивалось заданием завышенного (на три порядка) значения модуля Юнга заполнителя в поперечном направлении. Соответствие работы шпангоутов схеме единой нормали обеспечивалось заданием завышенных (на два порядка) значений их модулей поперечного сдвига. В модели КЭ-2 (в отличие от КЭ-1) задавалось реальное значение модуля Юнга заполнителя в поперечном направлении. В модели КЭ-3 (в отличие от КЭ-1 и КЭ-2) задавались реальные значения как модулей поперечного сдвига шпангоутов, так и модуля Юнга заполнителя в поперечном направлении.
Отметим, что разбиение шпангоутов на объемные элементы в КЭ-модели осуществлялось с выбором сетки, характерный размер ячейки которой составлял порядка 2 мм. Заполнитель заменялся однослойным ансамблем объемных элементов. При этом для большей части заполнителя размер сеточной ячейки в осевом и кольцевом направлениях выбирался порядка 3 мм. В окрестностях стыков со шпангоутами размер такой ячейки в осевом направлении уменьшался до 0,5 мм. Аналогичные по размерам ячейки имела и сетка оболочечных элементов на большей части каждого из несущих слоев. Исключение составляли лишь зоны краевых эффектов, где осуществлялось уменьшение осевых размеров оболочечных элементов до 0,2 мм. Отметим также, что для ансамблей оболочечных элементов, относящихся к внутреннему и наружному несущим слоям, в качестве поверхности приведения выбирались соответственно верхняя и нижняя поверхности слоя.
Для сравнения укажем, что расчеты на основе ЧИ-модели осуществлялись с выбором интервала между точками ортогонализации порядка 5 мм для трехслойных участков исследуемого объекта и порядка 20 мм для остальных его участков. При этом на каждом таком интервале интегрирование по схеме Кутта–Мерсона осуществлялось с выбором четырех шагов. По вопросу сходимости получаемого на основе ЧИ-модели решения (в рядах Фурье) поставленной задачи отметим, что выполненные расчеты с удержанием 60 и 120 гармоник в соответствующих Фурье-разложениях привели к практически совпадающим результатам.
6. Результаты численного моделирования
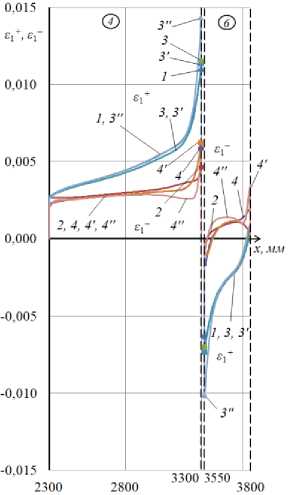
Полученные с применением построенных ЧИ- и КЭ-1-моделей результаты расчетов в виде графиков распределения (вдоль оси x) деформаций £1+, е2+ и £1", £2 на внешней и внутренней поверхности рассматриваемой конструкции (в осевом ее сечении, проходящем через вектор силы P (при ф = 0)), представлены на рис. 2 и 3. Цифрами 1 и 2 здесь обозначены кривые, относящиеся к ЧИ-модели, а цифрами 3 и 4 - к КЭ-1-модели. Отмечаем хорошее согласование представленных здесь результатов ЧИ- и КЭ-1-моделирований, что свидетельствует о достоверности получаемого численного решения рассматриваемой задачи. Отмечаем также, что наиболее напряженным является участок оболочки 4 в окрестности стыка с нагруженным шпангоутом 5. Наибольшего значения (порядка 0,011) здесь достигают (при ф = 0) меридиональные деформации £1+ на внешней поверхности оболочки 4 в точке стыка со шпангоутом 5. При этом в той же точке окружная деформация £2+ имеет в 10 раз меньшее значение (-0,00093). Максимальное (растягивающее) напряжение здесь оценивается величиной а1 = 198,4 МПа.
Для того чтобы оценить возможности снижения указанного уровня напряжений, в рассмотрение был также введен (второй) вариант обсуждаемой конструкции, в котором физико-механические характеристики материала шпангоутов 1 , 3 , 7 заданы в виде E 1 = 1,4 - 104 МПа, E 2 = 3,7 - 104 МПа, G 12 = 0,58 - 104 МПа, v21 = 0,18. Предварительные результаты расчетов с применением ЧИ- и КЭ-1-моделей показали, что при таком варианте напряжение G | в опасной на разрыв точке конструкции снижается на 17 % по сравнению с первоначальным вариантом и достигает величины 163,9 МПа.
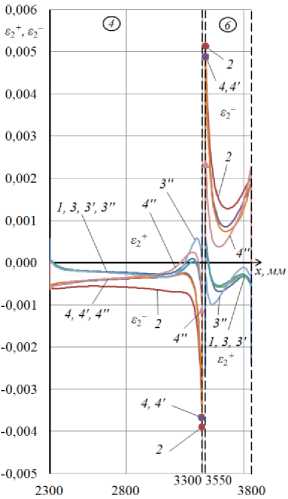
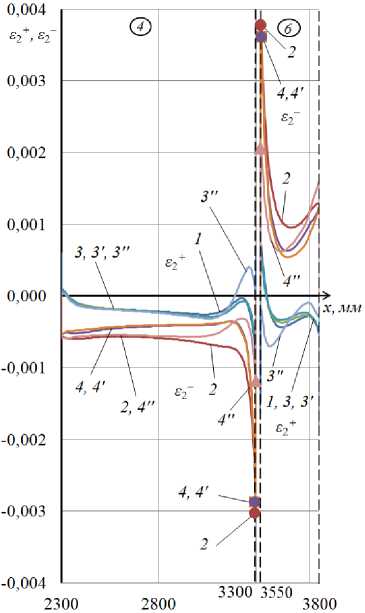
Графики распределения деформаций £ 1 +, £2+, £ 1" , £2 " по оболочке вдоль оси x при ф = 0 для первого и второго вариантов конструкции представлены соответственно на рис. 4 и 5. Цифрами 1 и 2 на графиках отмечены кривые, относящиеся к ЧИ-модели, цифрами 3 и 4 - к КЭ-1 модели, цифрами 3 ' и 4 ' - к КЭ-2-модели, цифрами 3" и 4" - к КЭ-3-модели (с принятием G 13 = G 23 = G 12 для материала шпангоутов).
Сравнение графиков, относящихся к моделям КЭ-1 и КЭ-2, показывает, что учет (в модели КЭ-2) сжимаемости заполнителя по толщине практически не влияет на получаемые расчетные результаты. Сравнение графиков, относящихся к модели КЭ-3 (учитывающей поперечные сдвиги в шпангоутах) и модели КЭ-1, позволяет сделать вывод, что учет обозначенных поперечных сдвигов приводит к увеличению пиковых значений меридиональных деформаций и напряжений в рассматриваемых конструктивных вариантах оболочки примерно на 30 %. В случае первого конструктивного варианта указанные пиковые значения приобретают вид s 1 = = 0,0144, G 1 = 259,2 МПа, а в случае второго варианта - 8 1 0,0122, G 1 = 219,6 МПа. Сравнивая эти результаты, приходим к окончательному выводу, что в рассматриваемом случае локального нагружения путем увеличения в 1,6 раза модуля Юнга материала шпангоутов в окружном направлении можно снизить примерно на 15 % уровень напряжений в исследуемой трехслойной оболочке.
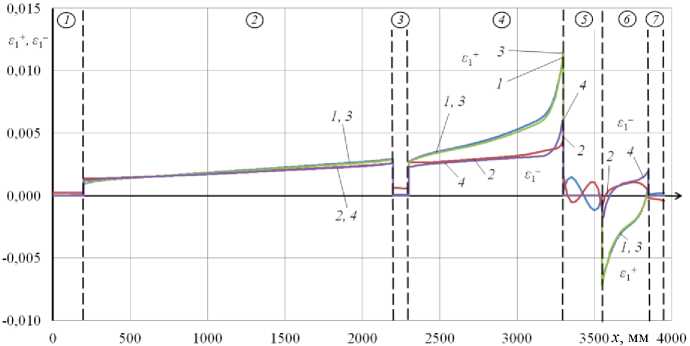
Рис. 2. Распределение вдоль оси x деформаций ε1 + , ε1 ‒ на внешней и внутренней поверхности рассматриваемой оболочки при φ = 0
Fig. 2. Distribution along the x-axis of strains ε1 + , ε1 ‒ on the outer and inner surfaces of the shell under consideration at φ = 0
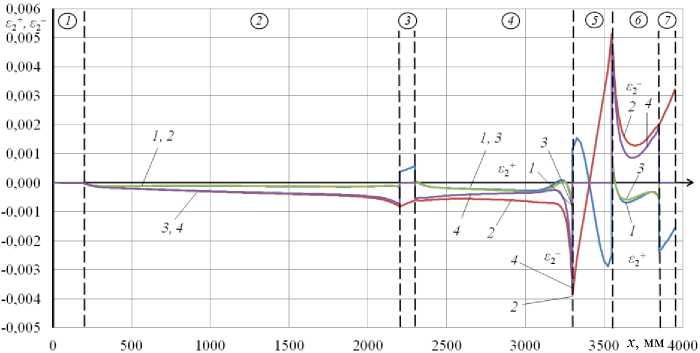
Рис. 3. Распределение вдоль оси x деформаций ε2 + , ε2 ‒ на внешней и внутренней поверхности рассматриваемой оболочки при φ = 0
Fig. 3. Distribution along the x-axis of strains ε2 + , ε2 ‒ on the outer and inner surfaces of the shell under consideration at φ = 0
б
а
Рис. 4. Распределение (по участкам 4 , 6 ) вдоль оси x деформаций на внешней и внутренней поверхности рассматриваемой оболочки при φ = 0 (первый вариант конструкции): а – ε1 + , ε1 ‒ ; б – ε2 + , ε2 ‒
Fig. 4. Distribution along the x-axis of strains on the outer and inner surfaces of the shell under consideration at φ = 0 (the first version of the design): a – ε1 + , ε1 ‒ ; b – ε2 + , ε2 ‒
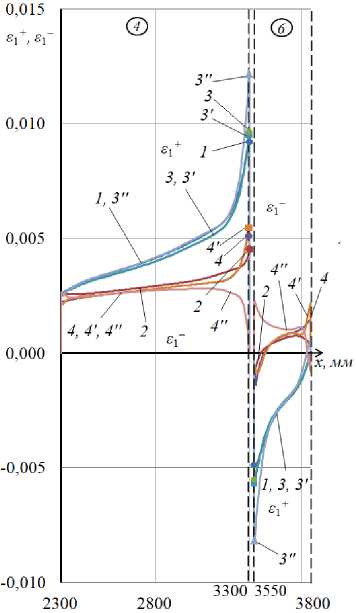
Рис. 5. Распределение (по участкам 4 , 6 ) вдоль оси x деформаций на внешней и внутренней поверхности рассматриваемой оболочки при φ=0 (второй вариант конструкции): а – ε1 + , ε1 ‒ ; б – ε2 + , ε2 ‒
б
Fig. 5. Distribution along the x-axis of strains on the outer and inner surfaces of the shell under consideration at φ=0 (the second version of the design): a – ε1 + , ε1 ‒ ; b – ε2 + , ε2 ‒
Заключение
На основе метода численного интегрирования и метода конечных элементов (комплекс ABAQUS, оболочечные элементы S4 и объемные элементы C3D20) построены вычислительные (ЧИ и КЭ) модели, ориентированные на решение задач о деформации локально нагруженных (через подкрепляющие шпангоуты) трехслойных с легким заполнителем композитных цилиндрических оболочек. В модели, основанной на методе численного интегрирования, принято, что трехслойные оболочки подчиняются гипотезе ломаной линии, а заполнитель несжимаем по толщине. Для шпангоутов при этом принята расчетная схема в виде короткой цилиндрической оболочки, подчиняющейся гипотезе единой нормали. Созданная КЭ-модель наделена возможностью (в варианте КЭ-1) быть настроенной (путем задания завышенных значений соответствующих модулей упругости) на решение задачи в постановке, близкой к ЧИ-модели. Таким образом, применительно к указанной постановке задачи реализованы две альтернативные вычислительные модели (ЧИ и КЭ-1). Методика получения (с подтвержденной достоверностью) искомого численного решения состоит в следующем. Сначала необходимо путем надлежащего выбора сетки конечных элементов добиться согласования расчетных результатов с применением ЧИ- и КЭ-1-моделей и тем самым подтвердить достоверность получаемого численным моделированием решения. Нахождение искомого решения затем осуществляется путем замены в модели КЭ-1 ранее завышенных значений модулей упругости на реальные. С применением предложенной методики выполнен расчет напряженно-деформированного состояния трехслойной с пенопластовым заполнителем композитной цилиндрической оболочки с четырьмя подкрепляющими шпангоутами, к одному из которых приложены две локальные осевые нагрузки. При этом установлено, что сжимаемость заполнителя в данном случае практически не влияет на результаты расчетов. Напротив, учет поперечных сдвигов в нагруженном шпангоуте приводит к повышению на 30 % получаемого расчетом уровня напряжений в оболочке на стыке с этим шпангоутом. Установлено также, что указанный уровень можно понизить примерно на 15 % путем увеличения в 1,6 раза модуля Юнга материала шпангоутов в окружном направлении.
Список литературы Численное моделирование локально нагруженных через шпангоуты трехслойных композитных цилиндрических оболочек
- Васильев В.В. Механика конструкций из композиционных материалов. - М.: Машиностроение, 1988. - 269 с.
- Артюхин Ю.П., Жигалко Ю.П., Сальников Г.М. Напряженно-деформированное состояние цилиндрической оболочки из стеклопластика при действии локальной нагрузки // Исследования по теории пластин и оболочек. - 1972. - Вып. 8. - С. 256-271.
- Нерубайло Б.В. Локальные задачи прочности цилиндрических оболочек. - М.: Машиностроение, 1983. - 248 с.
- Нерубайло Б.В. Прочность анизотропных цилиндрических оболочек при силовых и температурных воздействиях. - М.: Изд-во МАИ, 2018. - 160 с.
- Аналитические методы расчета локально нагруженных тонких оболочек / В.И. Лавинский, Д.И. Мазоренко, В.П. Ольшанский, Л.И. Тищенко. - Харьков: ХНТУСГ им. Петра Василенко; НТУ «ХПИ», 2009. - 366 с.
- Методы расчета цилиндрических оболочек из композиционных материалов / Ю.С. Соломонов, В.П. Георгиевский, А.Я. Недбай, В.А. Андрюшин - М.: Физматлит, 2009. - 264 с.
- Миткевич А.Б., Егоренков И.А., Протасов В.Д. Деформация шпангоута, связанного со стеклопластиковой оболочкой, под действием локальных нагрузок // Механика полимеров. - 1972. - № 5. - С. 854-860.
- Носова З.М., Отвечалин А.И. Экспериментально-теоретический анализ напряженно-деформированного состояния подкрепленных стеклопластиковых оболочек при действии локальных нагрузок //Механика полимеров. - 1975. - № 3. - С. 447-457.
- Носова З.М., Отвечалин А.И., Сухинин С.Н. Экспериментально-теоретический анализ деформированного состояния трехслойной конструкции со шпангоутами // Известия вузов. Машиностроение. - 1976. - № 7. - С. 189-190.
- Власов В.З. Общая теория оболочек и ее приложения в технике. - М.: Изд-во АН СССР, 1962. - 528 с.
- Бакулин В.Н. Метод конечных элементов для исследования напряженно-деформированного состояния трехслойных цилиндрических оболочек; ЦНИИ Информации. - М., 1985. - 140 с.
- Бакулин В.Н., Рассоха А.А. Метод конечных элементов и голографическая интерферометрия в механике композитов. - М.: Машиностроение, 1987. - 312 с.
- Noor A.K., Burton W.S. Assessment of computational models for multilayered composite shells // Appl. Mech. Rev. - 1990. - Vol. 43, no. 4. - P. 67-97.
- Noor A.K., Burton W.S., Bert C.W. Computational model for sandwich panels and shells // Appl. Mech. Rev. - 1996. - Vol. 49(3). - P. 155-199.
- Carera E. Theories and finite elements for multilayered, anisotropic, composite plates and shells // J. Arch. Comput. Meth. Eng. - 2002. - Vol. 9(2). - P. 87-140.
- Yaqoob Yasin M., Kapuria S. An efficient layerwise finite element for shallow composite and sandwich shells // Compos. Struct. - 2013. - Vol. 98. - P. 202-214.
- Бакулин В.Н., Инфлянскас В.В. Оценка локальных параметров сетки в конечно-элементных задачах // Вычислительная механика сплошных сред. - 2013. - Т. 6, № 1. - С. 70-77.
- Емельянов И.Г., Кузнецов А.В. Напряженное состояние оболочечных конструкций при локальных нагрузках // Проблемы машиностроения и надежности машин. - 2014. - № 1. - С. 53-59.
- Виноградов Ю.И. Расчет на прочность ортотропных локально нагруженных оболочек // Наука и Образование. - 2015. - № 03. - С. 68-84.
- Годунов С.К. О численном решении краевых задач для систем обыкновенных линейных дифференциальных уравнений // Успехи математических наук. - 1961. - Т. XVI, вып. 3. - С. 171-174.
- Статика и динамика тонкостенных оболочечных конструкций / А.В. Кармишин, В.А. Лясковец, В.И. Мяченков, А.Н. Фролов. - М.: Машиностроение, 1975. - 376 с.
- Григоренко Я.М., Василенко А.Т. Задачи статики анизотропных неоднородных оболочек. - М.: Наука, 1992. - 332 с.
- Королев В.И. Слоистые анизотропные пластинки и оболочки из армированных пластмасс. - М.: Машиностроение, 1965. - 272 с.
- Болотин В.В., Новичков Ю.Н. Механика многослойных конструкций. - М.: Машиностроение, 1980. - 375 с.
- Carera E. Historical review of Zig-Zag theories for multilayered plates and shells // Appl. Mech. Rev. - 2003. - Vol. 56. - P. 287-308.
- Meyer-Piening H.R. Application of the elasticity solution to linear sandwich beams, plates and shells analysis // J. Sandwich Struct. Mater. - 2004. - Vol. 6(4). - P. 295-312.
- Carera E., Briscotto S. A survey with numerical assessment of classical and refined theories for the analysis of sandwich plates // Appl. Mech. Rev. - 2009. - Vol. 62(20). - P. 1-17.
- Сухинин С.Н. Прикладные задачи устойчивости многослойных композитных оболочек. - М.: Физматлит, 2010. - 248 с.
- Use of axiomatic/asymptotic approach to evaluate various refined theories for sandwich shells / D.S. Mashat, E. Carera, A.M. Zenkour, S.A. Khateeb // Compos. Struct. - 2014. - Vol. 109. - P. 139-149.
- Григолюк Э.И. Уравнения трехслойных оболочек с легким заполнителем // Изв. АН СССР. Отд. техн. наук. - 1957. - № 1. - С. 77-84.
- Новожилов В.В. Теория тонких оболочек. - Л.: Судпромгиз, 1962. - 431 с.
- Сухомлинов Л.Г., Шиврин М.В. Численное моделирование напряженно-деформированного состояния подкрепленных шпангоутами трехслойных с легким заполнителем стеклопластиковых цилиндрических оболочек при локальных нагрузках // Космонавтика и ракетостроение. - 2017. - № 4(97). - С. 132-142.
- Сухомлинов Л.Г., Шиврин М.В. Применение вычислительной модели из объемных и оболочечных элементов при расчете локально нагруженных через шпангоуты трехслойных стеклопластиковых цилиндрических оболочек // Космонавтика и ракетостроение. - 2018. - № 3(102). - С. 92-102.


